“a为任意值时”的运用方法与技巧

☉湖北秭归县实验中学 李萍

“a为任意值时”的运用方法与技巧

☉湖北秭归县实验中学 李萍

受思维定式的影响，同学们容易解答有关常数或定值a的计算或证明题，但对于可以取任意值的a来说，一些同学常常无从下手、不知所措.其实，题目中告诉a为任意值时，或者告诉a为一定范围内的任何值时，就等于告诉我们，此范围中的a是可以取这个范围中的每一个值的，或者说对此范围中的每一个值都成立.把握了这一点，解题就有明确的方向了.下面以常见的四种类型为例加以说明.

一、取特殊值法

例1求证：不论a为何值，一次函数（2a-1）x-（a+3）y-（a-11）=0的图像恒过一定点.

分析：解决以“不论a为何值或a为任意实数”为条件的问题，可以取特殊值法.对于本题，可先取特殊值探求出定点，然后加以验证即可.

解：因为条件为不论a为何值，原一次函数的图像都经过一定点，所以我们不妨取a=0和a=1这两个特殊值来解答.

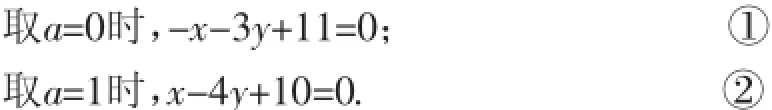
当x=2、y=3时，（2a-1）x-（a+3）y-（a-11）=2（2a-1）-3（a+3）-（a-11）=0成立.

所以不论a为何值，题中所给一次函数的图像恒过定点（2，3）.

例2当a为任意实数时，下列各式都有意义的是（）.

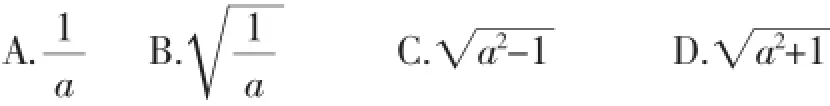
分析与解答：本题中，通过取特殊值，可以很快作出正确选择.比如，取a=0时，选择支A和B都不成立，再取a= 0.1时，选择支C不成立，但这两个值都可以使D成立，所以，本题的答案应该是D.取特殊值法是解答选择题的一种常用方法.

例3若3x2+4y-10=0，则15x3+3x2y+20xy+4y2+3x2-50x-6y=_______.

分析：本题与例1和例2不同，对任意一个x的值，y都有一个唯一的值和它对应，反之亦然.所以，选取特殊值时，必须使x和y同时满足二元不定方程3x2+4y-10=0，但这个二元不定方程的解有无数组，所以，取满足这个二元不定方程一组特殊值的原则是：要求代入所求的代数式中便于计算.

解：取二元不定方程3x2+4y-10=0的一组特殊的解代入待求式中，得15x3+3x2y+20xy+4y2+3x2-50x-

二、整体代入法

对于例3，我们还可以利用整体代入法来解答.此题的常规解法是用因式分解的方法，凑出3x2+4y这个因式，利用3x2+4y-10=0得到3x2+4y=10，再整体代入求解.

解：15x3+3x2y+20xy+4y2+3x2-50x-6y=（15x3+20xy）+（3x2y+4y2）+（3x2+4y）-50x-10y=5x（3x2+4y）+y（3x2+4y）+（3x2+4y）-50x-10y=50x+10y+10-50x-10y=10；

或者15x3+3x2y+20xy+4y2+3x2-50x-6y=（3x2+4y-10）×（5x+y+1）+10=10.

从第二种解答过程可以看出，本题还可以通过将原代数式化成“3x2+4y-10”这个整体的形式来解答.

例4求证：a、b为任意实数时，代数式2a2+4b2+8a-8b+15的值总是正数.

分析：要使原代数式为正数，将原代数式化成几个非负数的和（即整体）的形式即可.

证明：2a2+4b2+8a-8b+15=2（a2+4a）+4（b2-2b）+15= 2（a2+4a+4）+4（b2-2b+1）+3=2（a+2）2+4（b-1）2+3.

由（a+2）2≥0，（b-1）2≥0，得2a2+4b2+8a-8b+15≥3＞0.则代数式2a2+4b2+8a-8b+15的值总是正数.

三、分析推理法

例5设a为任意有理数，b为何值时有理系数方程2x2+（a+1）x-（3a2-4a+b）=0的根是有理数？

分析：2x2+（a+1）x-（3a2-4a+b）=0是一个一元二次方程，要使它的根为有理数，就必须使它的根的判别式是一个完全平方数，我们可以由此而分析推理得出想要的结果.

解：Δ=（a+1）2-4×2×［-（3a2-4a+b）］=a2+2a+1+24a2-32a+8b=25a2-30a+8b+1=（5a-3）2+8b-8.

因为根是有理数，a为任意有理数，（5a-3）2是一个完全平方式，并且是一个随a而变化的完全平方式，要使（5a-3）2+8b-8也为一个完全平方式，就只能是8b-8=0，由此求得b=1.

例6如图1，抛物线y=ax2+bx+c中，b、c是非零常数，无论a为何值（0除外），其顶点M一定在直线y=kx+b上，这条直线和x轴、y轴分别交于点E、A，且OA=OE.

（1）求k的值；

（2）求证：这条抛物线经过点A；

（3）经过点A的另一条直线y=mx+n和这条抛物线只有一个公共点，经过点M作x轴的平行线和直线y=mx+n交于点B，经过点B作x轴的垂线和这条抛物线交于点C，和直线y=kx+b交于点D，探索CD和BC的数量关系.

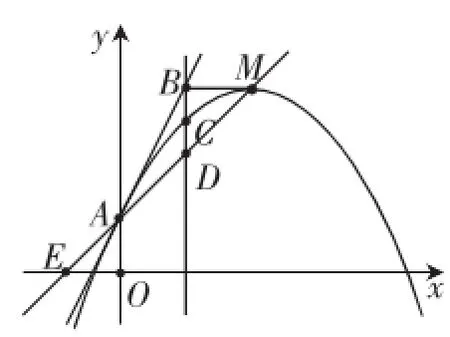
分析：本题是一道代数综合题，此类题常常是各地中考中的压轴题.如果我们的解题方法不得当，就会因此浪费时间并无法解答.但若掌握了方法、技巧，我们就可以快速解答并达到最好的效果.因为a为任意值，我们不可能取到每一个值，所以就要分析a在题中的特殊作用，然后依据其特殊性推理出恰当的方法来.

解：（1）由这条直线和x轴、y轴分别交于点E、A，且OA=OE，可知：

A点的坐标为（0，b），E点的坐标为（-b，0）.

将A（0，b）、E（-b，0）代入y=kx+b，可得k=1.

化简得：（4c-4b）a=b2-2b.

因为a为0以外的任何值时上述等式都成立，所以必有4c-4b=0和b2-2b=0同时成立.

则c=b=0（舍去）或c=b=2.

则A点的坐标为（0，2）.

则抛物线经过点A.

另解：也可以取两个特殊值得到点M的坐标，代入直线表达式y=kx+b，求出b、c的值.

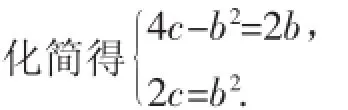
解这个方程组，同样可得到c=b=0（舍去）或c=b=2.

则A点的坐标为（0，2）.

则抛物线经过点A.

（3）由题意：方程mx+n=ax2+2x+2的判别式Δ=（2-m）2-4a（2-n）=0，且n=b，则（2-m）2=0，则m=2.

则BC=CD.

四、取一般值法

例7关于x、y的二元一次方程①：（a-1）x+（a+2）y+ 5-2a=0.

（1）当a=1时，得方程②；当a=-2时，得方程③.求②③组成的方程组的解.

（2）将求得的解代入方程①的左边，得到什么结果？由此可得什么结论？并验证你的结论.

分析与解答：读者千万别小看了此题，第二问基本上很多老师既不会写结论，也不会写验证方法.为了节约篇幅，下面边分析边解答.

（1）当a=1时，得方程②：3y+3=0.

当a=-2时，得方程③：-3x+9=0.

（2）将x=3、y=-1代入方程①的左边，得3（a-1）-（a+ 2）+5-2a=3a-3-a-2+5-2a=（3a-a-2a）+（-3-2+5）=0.

至此，学生的解答结束了.但（2）中还有两个“？”和一个“验证”没解决，而第二个“？”和一个“验证”让很多老师也为难了，这里先解决两个“？”.

第一个“？”：得到①式左边的值为0；

第二个“？”：取a为任意两个不同的值代入①中，得到两个二元一次方程，这两个方程的公共解一定是

“验证”对师生来说难度就更大了，但题目给学生提供了思考问题的方法，取特殊值法，验证的时候则需要反过来，即要一般化，此问实际上就是从特殊到一般的探究.验证过程如下：

取a=m代入①，得方程④：（m-1）x+（m+2）y+5-2m= 0.

再取a=n（n≠m）代入①，得方程⑤：（n-1）x+（n+2）y+ 5-2n=0.

④-⑤，得（m-n）x+（m-n）y-2m+2n=0.

即（m-n）x+（m-n）y=2（m-n）.

因为m≠n，所以得⑥：x+y=2.

以上四种方法，给出了“a为任意值”题型解题的一般方法与技巧，希望读者好好体会其中之真谛.