大面积纳米压印揭开式脱模机理和规律
2017-03-09李延强兰红波
李延强 兰红波
青岛理工大学纳米制造与纳光电子实验室,青岛,266033
大面积纳米压印揭开式脱模机理和规律
李延强 兰红波
青岛理工大学纳米制造与纳光电子实验室,青岛,266033
针对大面积纳米压印脱模工艺,开展了揭开式脱模机理和规律的研究。基于界面黏附能理论,建立了气体辅助揭开式脱模力预估模型;基于应变能法和脱模过程中能量守恒定律,建立了气体辅助揭开式脱模临界脱模速度模型。利用ABAQUS工程数值模拟软件,分析得到纳米压印工艺参数(脱模力、脱模角度、脱模速度)对揭开式脱模的影响规律。
大面积纳米压印;揭开式脱模;脱模力;脱模速度
0 引言
纳米压印光刻(nanoimprint lithography, NIL)是一种接触式几何约束流变成形方法,该方法包括两个基本的工艺过程,即压印过程和脱模过程。脱模对于压印图形的最终质量、面积、缺陷控制以及模具使用寿命有着重要的影响[1-2],尤其是对于大面积纳米压印、晶圆级纳米压印以及高深宽比微纳结构压印,脱模已经成为最大的挑战性难题,是制约大面积纳米压印广泛工业化应用的最大瓶颈。
根据压印工艺和使用模具的不同,现有纳米压印光刻主要采用以下两种脱模方法:①平行式脱模(parallel demolding),模具(硬模具)与固化后的压印材料特征结构整体平行分离;②“揭开”式脱模(peel-off demolding),模具(软模具)与固化后的压印材料特征结构逐渐分离。对于大面积纳米压印,揭开式脱模已经被看作是最为有效的一种脱模方法,特别是气体辅助揭开式脱模是大面积纳米压印最理想的脱模方案。目前,国内外学者对于整体平行式脱模已经开展了深入的研究[3-5],但是,对于揭开式脱模的研究则较少,尤其是有关揭开式脱模机理、影响因素等方面的研究几乎还是空白。针对揭开式脱模的机理和规律,本文开展了理论建模以及数值模拟的系统研究。
1 理论模型
1.1 脱模力
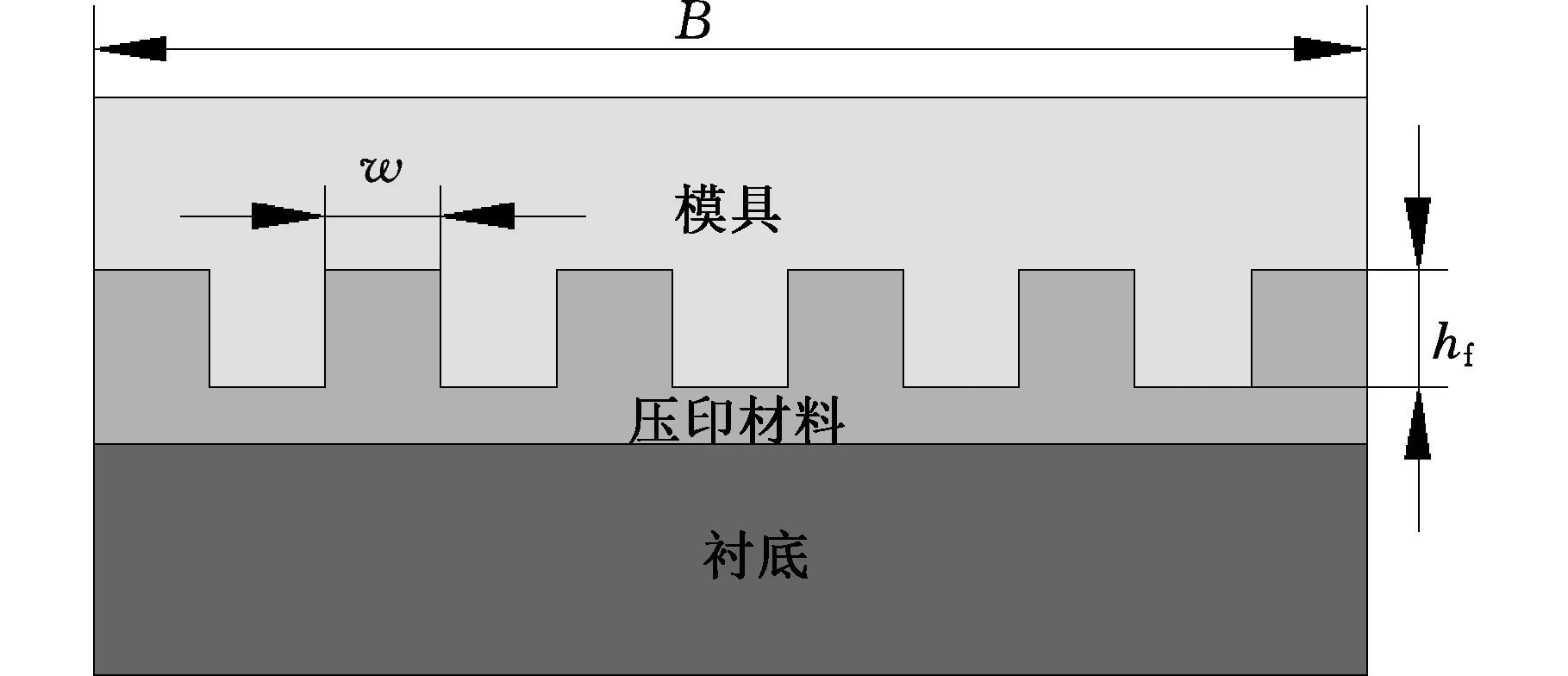
相比于整体平行式脱模,“揭开”式脱模采用线性逐渐分离的方法(图1),依靠较小的脱模力就能实现大面积脱模。
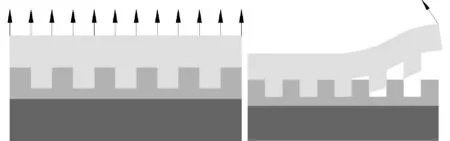
(a)整体平行式脱模 (b)揭开式脱模图1 纳米压印两种脱模方式示意图Fig.1 Methods of demolding for NIL
整个纳米压印系统包括4个表面和2个界面:模具下表面、衬底上表面、压印材料上表面和下表面;模具与压印材料形成的界面以及衬底与压印材料形成的界面,不同的表面和界面以及同一界面在压印过程中的不同阶段具有不同甚至完全相反的特性。例如,压印过程中,为了实现压印材料对于模具特征结构腔体的快速和完全填充,压印材料与模具界面应该具有良好的浸润性。然而,在脱模过程中,则要求固化后的压印材料上表面与模具表面所形成的界面具有非浸润特性,以利于脱模。同时,固化后的压印材料下表面与衬底之间应呈现浸润特性,以拥有良好的黏附性,避免脱模时固化后的压印材料与衬底的分离和卷曲。
基于以上分析可知,成功地脱模需要满足以下条件:即脱模力大于模具与压印材料之间的界面黏附力,以实现模具与固化后压印结构的分离;同时脱模力小于压印材料与衬底之间的界面黏附力,确保脱模过程中压印材料与衬底不发生分离,即有
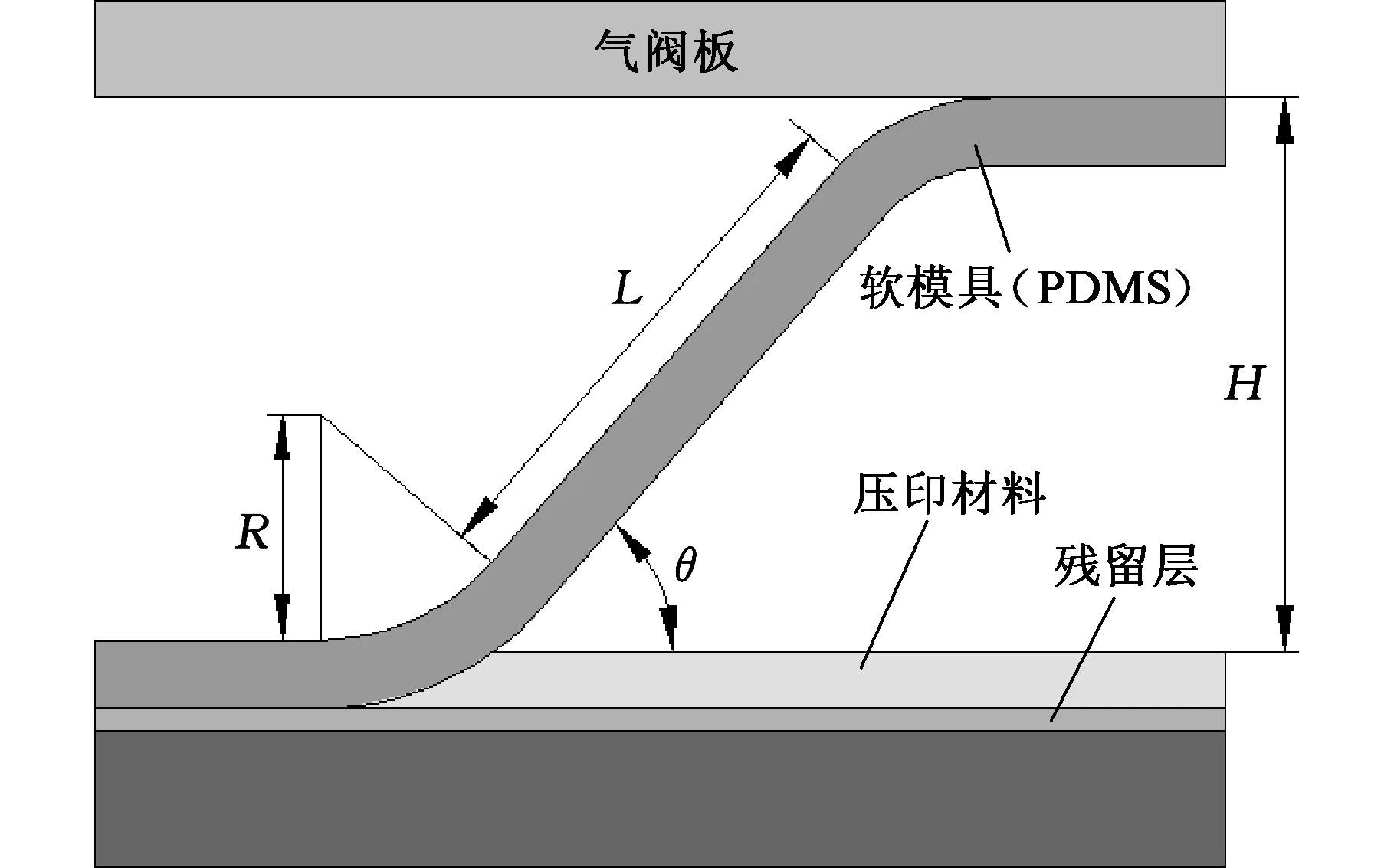
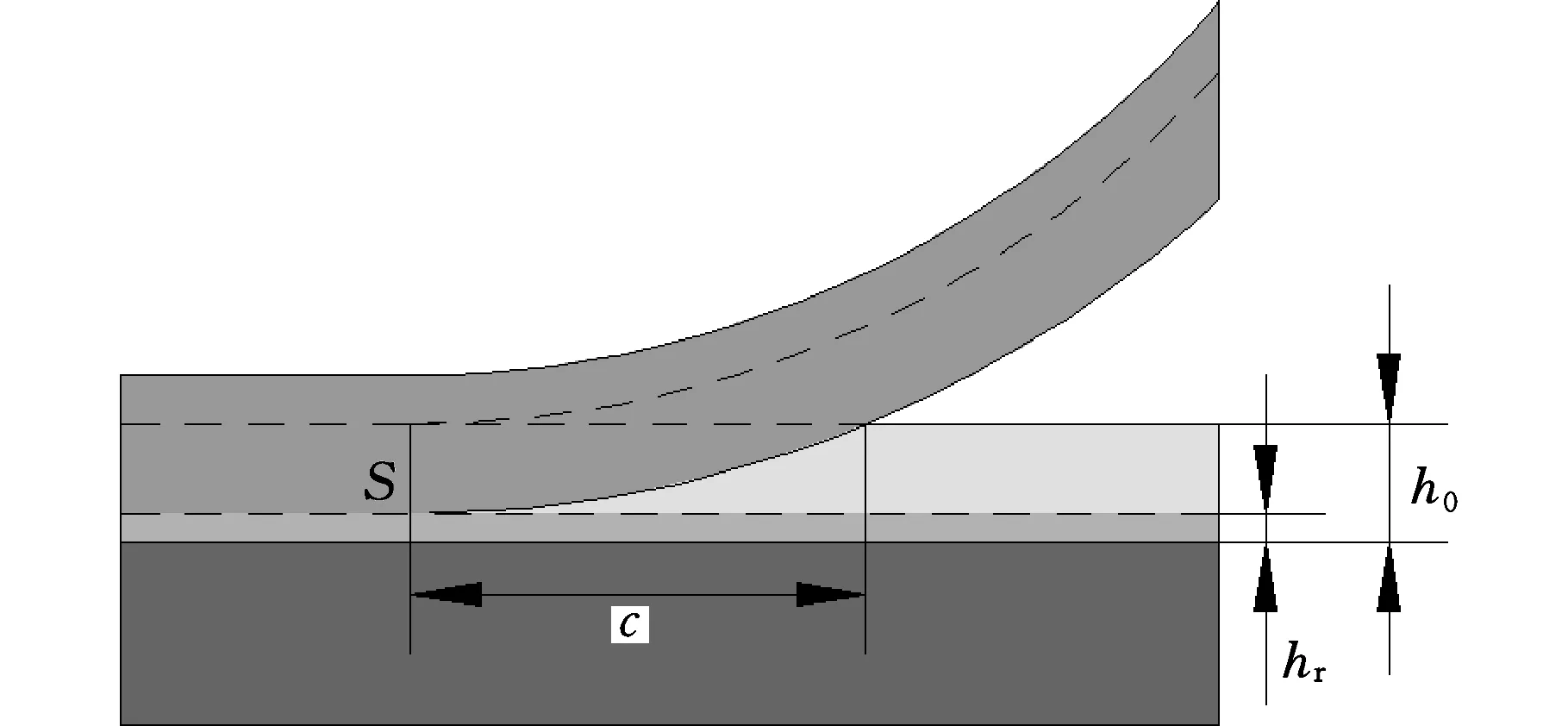
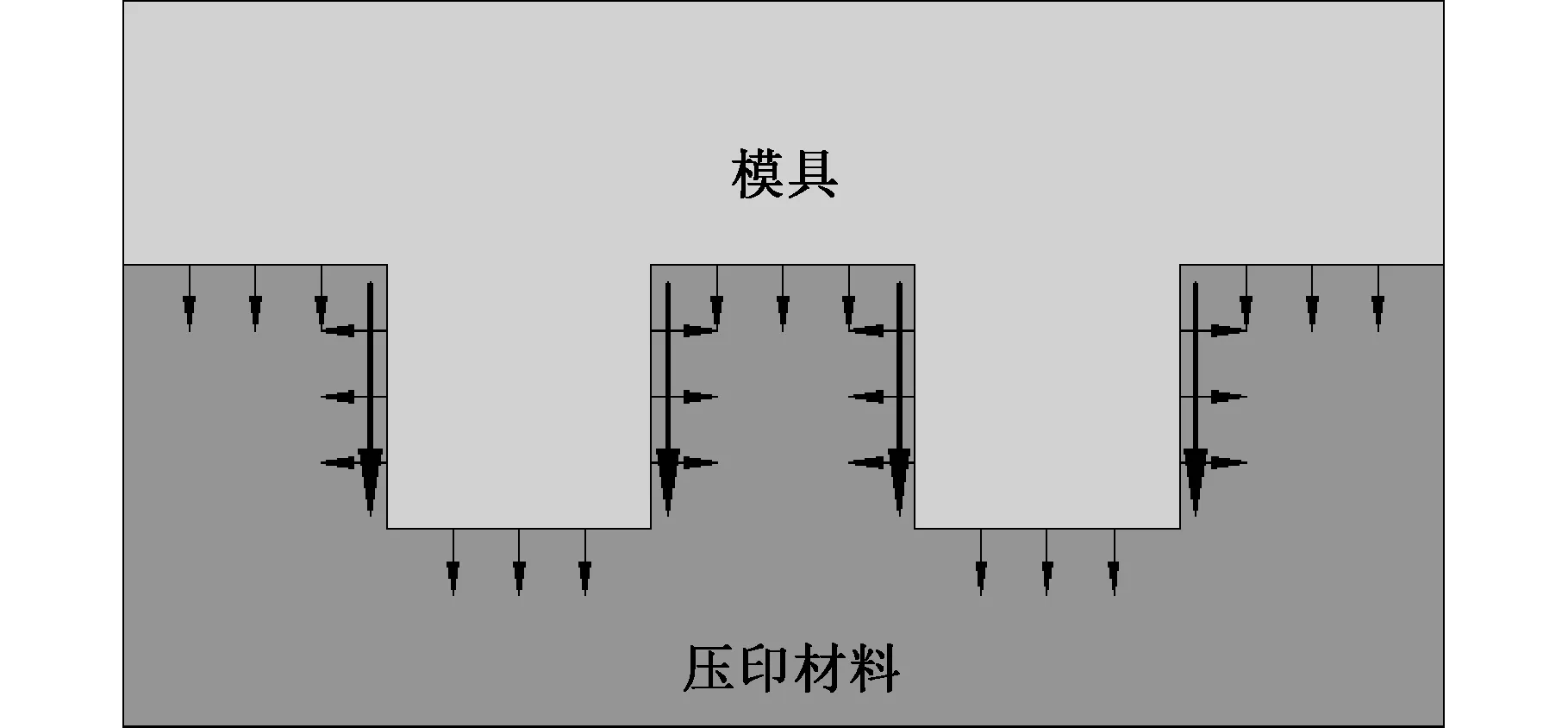
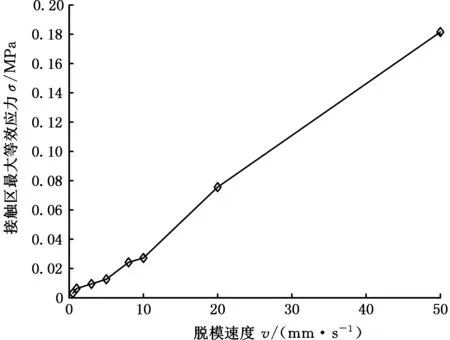
F1 (1) 其中,F1为模具与压印材料之间的界面黏附力;F2为压印材料与衬底之间的界面黏附力;F为施加在模具上的脱模力。 脱模实际上就是破坏模具与压印材料之间的黏附力,因此首先讨论界面黏附力。 1.1.1 界面黏附力 两相互接触物体的界面黏附能包含2个部分:色散分量(dispersioncomponents)和极性分量(polarcomponents),两分量遵守界面间分子力线性相加原理[6],界面黏附能表示为 (2) 由于固体的表面能难以直接测定,两接触固体的界面黏附能一般借助于固液界面黏附能间接求得:即首先通过固液界面接触角法求得两固体表面能的极性分量和色散分量,然后再获得两固体界面黏附能[7]。具体过程如下: 固液界面黏附能的色散分量和极性分量可由液体表面张力的色散分量和极性分量表示[8],即 (3) 根据Young方程[9],固液界面黏附能为 Els=γl(1+cosθe) (4) 式中,θe为固液界面接触角;γl为液体表面张力。 将式(3)、式(4)联立方程组,得 (5) 对于某种确定的固液系统,分别测量2种已知表面张力极性分量和色散分量的测试溶液在固体表面的接触角,然后将其分别代入式(5),联立方程组即可求得该固体表面能的色散分量和极性量。 对于两固体界面黏附能Eab,根据SEO等[10]的研究结果,有下列关系: (6) 则黏附力与黏附能和接触长度的关系为[11] Fab=EabD (7) 式中,Fab为两固体界面黏附力;D为两固体接触线长度。 图2 脱模微观结构示意图Fig.2 The micro-structure of demolding 因此,模具与压印材料界面黏附力F1以及压印材料与衬底界面黏附力F2分别为 (8) F2=ErsB (9) 其中,Emr为模具与压印材料的界面黏附能;Ers为压印材料与衬底的界面黏附能;Emr和Ers可以用式(6)求出。 1.1.2 气体辅助脱模力 纳米压印通常采用气体辅助式脱模,脱模力即为负压(真空吸力)所形成的气压力,因此为了与传统机械式脱模力相区别,本文所述气压式脱模力用符号P表示。 图3是揭开式脱模原理图,图中各部分及符号代表的含义如下:H为压印材料与气阀板之间的距离,L为脱模力施加长度,θ为脱模角度,R为脱模过程中的折弯半径。 图3 揭开式脱模原理图Fig.3 The schematic diagram of peel-off demolding 图4为揭开式脱模局部放大图,其中各符号含义如下:h0为压印材料初始厚度,hr为参与图形转移的压印材料残留层的厚度,c为脱模区间的长度,S为单个特征图案侧壁面积。 图4 揭开式脱模局部放大示意图Fig.4 The partial enlargement of peel-off demolding 图5 揭开式脱模微观示意图Fig.5 The micro-structure of peel-off demolding 对于揭开式脱模,主要克服上下表面和侧壁的黏附力以及侧壁的摩擦力(图5);下面分别讨论上下表面和侧壁在脱模过程的能量关系。 对于上下表面,能量守恒有下列关系: (10) 其中,Wp为脱模力对系统所做的功,Up为储存的弹性应变能,Tp为模具的动能,Ep为脱模过程中上下表面不可恢复消耗功,Ap为水平面接触总面积。上下表面所需的脱模力P1为 (11) 与上下表面作用机理不同,侧壁不可恢复的耗散功Es是由作用在侧壁摩擦耗散的功Ef和克服接触面黏附作用的功Ea两部分构成,As表示侧壁的总面积。此时侧壁的能量守恒式为 (12) 侧壁所需的脱模力为 (13) 式中,σ为表面接触应力;μ为摩擦因数。 式(11)、式(13)中的Wn表示脱模过程中压印材料与模具的界面黏附能。为了实现模具与压印材料的脱离, 脱模过程中不可耗散功E的平均能量释放率要大于Wn,即有 (14) 其中,E为脱模过程中总的不可恢复耗散功,E=Ep+Ea;A为脱模过程中模具与压印材料总的接触面积,A=Ap+As。 则揭开式脱模所需脱模力P为 (15) 1.2 脱模临界速度 MEITL等[12]通过研究发现:在脱模过程中,当脱模速度较大时,模具与压印材料有可能作为一个整体从衬底上被分离,导致脱模失败。当脱模速度降低到某一阈值时,才能确保模具与压印材料分离,并且压印材料与衬底之间不分离,实现成功脱模。为了获得高的脱模效率,希望脱模速度越快越好;但是,为了确保成功、高质量脱模,则脱模速度越慢越好。因此,对于一个确定的压印系统(模具、压印材料、衬底),存在一个临界脱模速度vc,既能保证成功脱模,又能获得最大的脱模效率。 不同的脱模速度对脱模结果的影响可以从能量释放率的角度进行解释,脱模力与能量释放率有以下关系: (16) 其中,G为压印材料与模具脱离时,不可恢复消耗功的平均能量释放速率,K为模具已脱离压印材料表面的宽度。能量释放速率G与脱模速度v的表达式为 (17) 式中,G0为初始能量释放速率;v0为初始脱模速度;n为换算因子。 临界速度vc表达式如下: (18) 脱模初始时,脱模速度趋于0,则动能为0;此时作用在模具上的脱模力没有使压印材料与模具产生分离,也没有发生弹性变形,故弹性应变能U为零。因而外力所做的功全部转化为不可恢复的耗散功E。因此对于上下表面,有下列关系: (19) (20) 和上下表面相同,压印材料与模具的侧面在初始脱模时弹性应变能U为零,外力所做的功全部转化为不可恢复的耗散功E,此时的能量守恒式为 (21) (22) 故脱模初始时,模具与压印材料分离所需脱模力P0为 (23) 则G0表达式为 (24) 在式(20)和式(22)~式(24)中,En为压印材料与模具间的黏附能;由于在速度趋于零时,压印材料与模具没有发生分离,此时的黏附能En可由式(6)进行计算。 对于脱模的任意阶段,释放速率G为 (25) 将式(24)、式(25)代入式(18),则临界速度vc为 (26) 为了进一步揭示揭开式脱模的机理和规律,下面采用ABAQUS通过数值模拟的方法研究脱模工艺参数对揭开式脱模的影响。 (1)几何建模。模具材料为PDMS,压印材料为PUA,两种材料的基本属性[13]见表1。衬底材料为蓝宝石。模具特征结构高度hf和宽度w均为2μm。 表1 模具图形层PDMS和压印材料PUA主要参数Tab.1 The main parameters of PDMS and PUA (2)载荷和边界条件。蓝宝石衬底两侧施加完全约束,压印材料与模具两侧施加X向约束;在模具上表面右上角施加脱模力。 (3)网格划分。对于模具与衬底,网格类型由平面应变族的四边形与三角形网格组合构成;对于压印材料,网格类型由黏性族的四边形网格构成。 2.1 脱模力 在模具右上角分别施加5 N、10 N、15 N、20 N、25 N、30 N 6个不同数值的脱模力。不同脱模力作用下脱模系统应力云图见图6~图11;模具与压印材料接触区域最大等效应力折线图见图12。 图6 脱模力为5 N时脱模系统应力云图(最大等效应力为1.622 kPa)Fig.6 The stress equivalent under 5 N demolding force(the max equivalent stress is 1.622 kPa) 图7 脱模力为10 N时脱模系统应力云图(最大等效应力为2.920 kPa)Fig.7 The stress equivalent under 10 N demolding force(the max equivalent stress is 2.920 kPa) 图8 脱模力为15 N时脱模系统应力云图(最大等效应力为4.542 kPa)Fig.8 The stress equivalent under 15 N demolding force(the max equivalent stress is 4.542 kPa) 图9 脱模力为20 N时脱模系统应力云图(最大等效应力为6.488 kPa)Fig.9 The stress equivalent under 20 N demolding force(the max equivalent stress is 6.488 kPa) 图10 脱模力为25 N时脱模系统应力云图(最大等效应力为9.083 kPa)Fig.10 The stress equivalent under 25 N demolding force(the max equivalent stress is 9.083 kPa) 图11 脱模力为30 N时脱模系统应力云图(最大等效应力为13.30 kPa)Fig.11 The stress equivalent under 30 Ndemolding force(the max equivalent stress is 13.30 kPa) 基于以上结果,得到以下结论:随着脱模力增大,模具与压印材料接触区域最大等效应力近似呈线性增长。当脱模力小于20 N时,接触区域最大等效应力增长较为缓慢;当脱模力大于20 N时,接触区域最大等效应力增长迅速。因此,脱模力以20 N左右最宜。 2.2 脱模角度 在模具右上角施加大小为20 N的脱模力,脱模角度分别选取0°、30°、45°、60°、90° 5个角度;不同脱模角度下脱模系统应力云图如图13~图17所示;图18为模具与压印材料接触区域最大等效应力折线图。 图13 角度为0°时脱模系统应力云图(最大等效应力为12.98 kPa)Fig.13 The stress nephogram under angle 0°demolding angle(the max equivalent stress is 12.98 kPa) 图14 角度为30°时脱模系统应力云图(最大等效应力为11.84 kPa)Fig.14 The stress nephogram under angle 30°demoldingangle(the max equivalent stress is 11.84 kPa) 图15 角度为45°时脱模系统应力云图(最大等效应力为8.091 kPa)Fig.15 The stress nephogram under angle 45°demoldingangle(the max equivalent stress is 8.091 kPa) 图16 角度为60°时脱模系统应力云图(最大等效应力为7.895 kPa)Fig.16 The stress nephogram under angle 60°demoldingangle(the max equivalent stress is 7.895 kPa) 图17 角度为90°时脱模系统应力云图(最大等效应力为3.242 kPa)Fig.17 The stress nephogram under angle 90°demoldingangle(the max equivalent stress is 3.242 kPa) 基于以上结果,得到以下结论:①随着脱模角度增大,模具与压印材料接触区域最大等效应力逐渐减小。②脱模角度由0°增大到30°以及由45°增加大60°时,最大等效应力减小较为缓慢;脱模角度由30°增大到45°以及由60°增大到90°时,最大等效应力减小较为迅速。③脱模角度为30°时,能够保证气阀板与模具有较大的接触面积(脱模气压力源于作用在模具与气阀板接触面上的压强)从而使接触区域产生较大的等效应力;因此,脱模角度以30°最为合适。 2.3 脱模速度 模具右上角施加大小为20 N的脱模力,脱模角度为30°。分别施加0.5 mm/s,1 mm/s,3 mm/s,5 mm/s,8 mm/s,10 mm/s,20 mm/s,50 mm/s不同的脱模速度,不同脱模速度下脱模系统应力云图见图19~图26,模具与压印材料接触区域最大等效应力折线图见图27。 图19 脱模速度为0.5 mm/s时脱模系统应力云图(最大等效应力为3.154 kPa)Fig.19 The stress nephogram under 0.5 mm/s demoldingvelocity(the max equivalent stress is 3.154 kPa) 图20 脱模速度为1 mm/s时脱模系统应力云图(最大等效应力为6.308 kPa)Fig.20 The stress nephogram under 1 mm/s demolding velocity(the max equivalent stress is 6.308 kPa) 图21 脱模速度为3 mm/s时脱模系统应力云图(最大等效应力为9.462 kPa)Fig.21 The stress nephogram under 3 mm/s demolding velocity(the max equivalent stress is 9.462 kPa) 图22 脱模速度为5 mm/s时脱模系统应力云图(最大等效应力为12.62 kPa)Fig.22 The stress nephogram under 5 mm/s demolding velocity(the max equivalent stress is 12.62 kPa) 图23 脱模速度为8 mm/s时脱模系统应力云图(最大等效应力为24.18 kPa)Fig.23 The stress nephogram under 8 mm/s demolding velocity(the max equivalent stress is 24.18 kPa) 图24 脱模速度为10 mm/s时脱模系统应力云图(最大等效应力为27.20 kPa)Fig.24 The stress nephogram under 10 mm/s demolding velocity(the max equivalent stress is 27.20 kPa) 图25 脱模速度为20 mm/s时脱模系统应力云图(最大等效应力为75.58 kPa)Fig.25 The stress nephogram under 20 mm/s demolding velocity(the max equivalent stress is 75.58 kPa) 图26 脱模速度为50 mm/s时脱模系统应力云图(最大等效应力为181.5 kPa)Fig.26 The stress nephogram under 50 mm/s demolding velocity(the max equivalent stress is 181.5 kPa) 图27 不同速度下接触区域最大等效应力折线图Fig.27 The max stress line chart under different demolding velocity 基于以上结果,得到以下结论:当脱模速度小于10 mm/s时,模具与压印材料接触区域最大等效应力整体较小且增大比较缓慢;当速度大于10 mm/s时,最大等效应力整体较大且增大迅速。因此,对于该脱模系统当脱模速度为10 mm/s时,脱模效率最高同时脱模效果也最好,即脱模临界速度为10 mm/s。 (1)基于界面黏附能理论,建立了气体辅助揭开式脱模力预估模型。基于应变能法和脱模过程中能量守恒定律,建立了气体辅助揭开式脱模临界脱模速度理论模型。 (2)随着脱模力的增大,模具与衬底接触区域最大等效应力近似呈线性增长,本文所述脱模系统的最佳脱模力为20 N。随着脱模角度增大,接触区域最大等效应力逐渐减小,本文所述脱模系统中,脱模角度为30°时,能够保证气阀板与模具有较大的接触面积,从而使接触区域产生较大的等效应力,因此脱模角度以30°最为合适。合适的脱模速度既能保证成功脱模,又能获得最大的脱模效率,在本文所述脱模系统中,脱模速度为10 mm/s时,能够同时保证脱模效率以及脱模质量,即脱模临界速度为10 mm/s。 [1] DIRCKX M E, HARDT D E. Analysis and Characterization of Demolding of Hot Embossed Polymer Microstructures[J]. Journal of Micromechanics and Microengineering. 2011, 21, 085024. [2] SCHICHFT H. Nanoimprint Lithography: an Old Story in Modern Times a Review[J]. Journal of Vacuum Science & Technology B, 2008, 26: 458-480. [3] TRABADELO V, SCHIFT H, MERINO S, et al. Measurement of Demolding Forces in Full Wafer Thermal Nanoimprint[J]. Microelectronic Engineering, 2008, 85: 907-909. [4] ALBORZ A, LEE J J, SUNGGOOK P. Surface Adhesion and Demolding Force Dependence on Resist Composition in Ultraviolet Nanoimprint Lithography[J]. Applied Surface Science, 2011, 258: 1272-1278. [5] DIRCKX M E. Demolding of Hot Embossed Polymer Microstructures[D]. Cambridge: Massachusetts Institute of Technology, 2010. [6] WANG Z, ZHANG J, XING R, et al. Micropatterning of and Organic Semiconductor Microcrystalline Materials OFET Fabrication by “Hot Lift Off”[J]. Journal of the American Chemical Society, 2003, 125:15278-15279. [7] HUNG Y L, CHANG Y Y, WANG M J, et al . A Simple Method for Measuring the Superhydrophobic Contact Angle with High Accuracy[J]. Review of Scientific Instruments, 2010,81(6):65-105. [8] WU S. Polymer Interface and Adhesion[M]. New York: Marcel Dekker Inc., 1982:6-104. [9] 胡福增. 材料表面与界面[M]. 上海:华东理工大学出版社, 2007: 15-18. HU Fuzeng. The Surface and Interface of Materials[M]. Shanghai: East China University of Science and Technology Press, 2007: 15-18. [10] SEO S M, PARK J J, LEE H H. Micropatterning of Metal Substrate by Adhesive Force Lithography [J]. Applied Physics Letters, 2009, 86 (13):133-114. [11] JIANG W, LIU H, DING Y, et al. Investigation of Ink Transfer in a Roller-reversal Imprint Process [J]. Journal of Micromechanics and Microengineering, 2009,19:015-033. [12] MEITL M A, ZHU Z T, KUMAR V, et al. Transfer Printing by Kinetic Control of Adhesion to an Elastomeric Stamp [J]. Nature Materials, 2006,5:33-38. [13] LAN H, LIU H. UV-nanoimprint Lithography: Structure, Materials and Fabrication of Flexible Molds[J]. Journal of Nanoscience and Nanotechnology, 2013, 13: 3145-3172. (编辑 王艳丽) Mechanism and Laws of Peel-off Demolding for Large-area Nanoimprint Lithography LI Yanqiang LAN Hongbo Nanomanufacturing and Nano-optoelectronics Lab,Qingdao Technological University,Qingdao,Shandong,266033 This paper investigated the mechanism and influencing factors of peel demolding for large-area nanoimprint lithography. A model estimating the air pressure-assisted peel-off demolding forces was established based on the interfacial adhesion energy. A model of predicting the critical speed of air pressure-assisted peel-off demolding was derived by the combination of the strain energy method and the conservation of energy in demolding stage. Furthermore, the influences and laws of the demolding process parameters(demolding force, demolding angle, demolding speed) were revealed by numerical simulation using ABAQUS software. large-area nanoimprint lithography; peel-off demolding; demolding force; demolding speed 2016-04-28 国家自然科学基金资助项目(91023023,51375250);青岛市创业创新领军人才计划资助项目(13-CX-18) TN305 10.3969/j.issn.1004-132X.2017.04.016 李延强,男,1992年生。青岛理工大学机械工程学院硕士研究生。主要研究方向为微纳米制造、纳米压印。兰红波(通信作者),男,1970年生。青岛理工大学机械工程学院教授、博士研究生导师。E-mail:hblan99@126.com。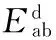
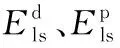
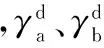

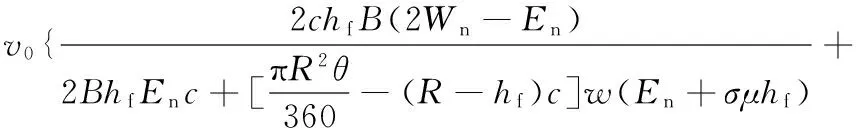
2 数值模拟




















3 结论
