三排柱式回转支承非理想Hertz接触特性分析
2017-03-09冯建有戚晓利童靳于
冯建有 戚晓利 童靳于
安徽工业大学机械工程学院,马鞍山,243032
三排柱式回转支承非理想Hertz接触特性分析
冯建有 戚晓利 童靳于
安徽工业大学机械工程学院,马鞍山,243032
传统方法对三排柱式回转支承的滚柱与滚道间的接触分析都是基于Hertz接触理论,然而滚柱与滚道的实际接触超出了Hertz接触理论的范围。针对该问题,重点研究了滚柱与滚道的非理想Hertz接触特性,得出了接触变形及接触应力沿滚柱轴向的变化规律。结合McEwen关于圆柱体法向接触理论,推导了滚柱与滚道接触区内部的应力场各应力分量解析表达式,并讨论了滚道失效与应力之间的关联。最后,建立了滚柱与滚道接触的3D有限元模型,仿真结果表明,接触区的应力分布与解析解基本吻合,结论可为三排柱式回转支承的设计与制造提供参考。
柱式回转支承;非理想Hertz接触;接触应力;应力分布
0 引言
三排柱式回转支承是盾构机、回转窑及起重机等重型工程机械所必需的重要传力元件,其运行及受力的主要特点是低速、重载[1-4]。回转支承构件一旦发生故障或失效,不仅会影响主机乃至整条生产线的生产效益,严重的还会导致重大的设备事故和人身事故以及巨大的经济损失[5-7]。回转支承的主要失效形式有两种,分别为滚道损坏和断齿,其中滚道损坏占的比例达98%以上[8]。因此,充分了解回转支承在外载荷作用下,滚动体与滚道之间的接触应力及接触区各应力分量的大小与分布特点,对合理选用及科学维护回转支承具有非常重要的意义。
当前,国内外对球式回转支承关于滚道压力分布、接触特性、承载能力及寿命等方面的研究较多[9-12],而针对三排滚柱式回转支承接触特性的研究相对较少[13-16]。KANIA[17]针对柱式回转支承,分别建立了单个滚柱与滚道接触的3D和2D有限元模型,研究了负载与接触应力及变形之间的关系,并讨论了网格密度对计算结果的影响。文献[13-16]利用有限元法建立了三排柱滚柱式回转支承静态、动态承载能力的计算模型,讨论了轴向间隙对其滚道压力分布、承载能力及寿命的影响,并研究了滚道表面接触应力及滚道潜层的应力分布规律。
上述研究大多采用有限元方法分析柱式回转支承的接触问题,能够较好地模拟滚柱与滚道的接触特性,但该方法针对不同型号的回转支承需要分别建模,计算工作量庞大。因此,研究滚柱与滚道接触特性的解析解既有理论意义,又有工程应用价值。目前,针对三排柱式回转支承的接触分析主要是基于Hertz接触理论,然而滚柱与滚道在实际接触过程中,滚柱具有有限长度这一特征超出了Hertz理论的范围。虽然Hertz理论准确地预测了滚柱大部分长度上的接触应力,但是紧靠滚柱两端处会出现明显偏差[18]。针对这一问题,本文以柱式回转支承为研究对象,讨论了回转支承中滚柱与滚道的非理想Hertz接触问题,得到了沿滚柱轴向的接触变形和接触应力的分布。在此基础上,结合McEwen关于圆柱体二维法向接触理论,本文进一步讨论了三排柱回转支承滚柱与滚道接触区的应力场分布,得到了滚道表面及潜层的Von Mises应力及最大切应力的分布特点。最后,借助有限元软件建立了回转支承滚动体与滚道的弹性接触有限元模型。
1 滚柱最大接触载荷
柱式回转结构如图1所示,其中上下两排滚柱称为轴向滚柱,中间一排滚柱称为径向滚柱,其受力状况如图2所示,从工程机械的实际工况来看,作用于回转支承的载荷有轴向载荷Fa、倾覆力矩MT及径向载荷Fr,轴向载荷和倾覆力矩由上下两排轴向滚柱承受,径向载荷由中间一排径向滚柱承受,而在实际工况中三排柱式回转支承承受的径向载荷较前两种载荷要小得多,故本文中重点讨论轴向滚柱的受力。根据文献[14,19],滚柱与滚道之间的最大接触载荷Qmax计算公式如下:
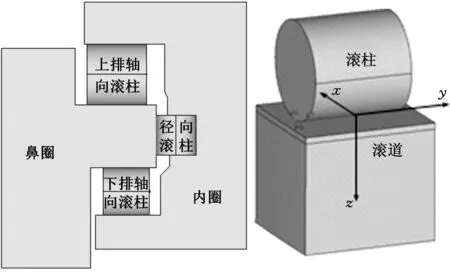
(a)横截面(b)滚柱与滚道图1 三排柱式回转支承结构简图Fig.1 Three-row roller slewing bearing
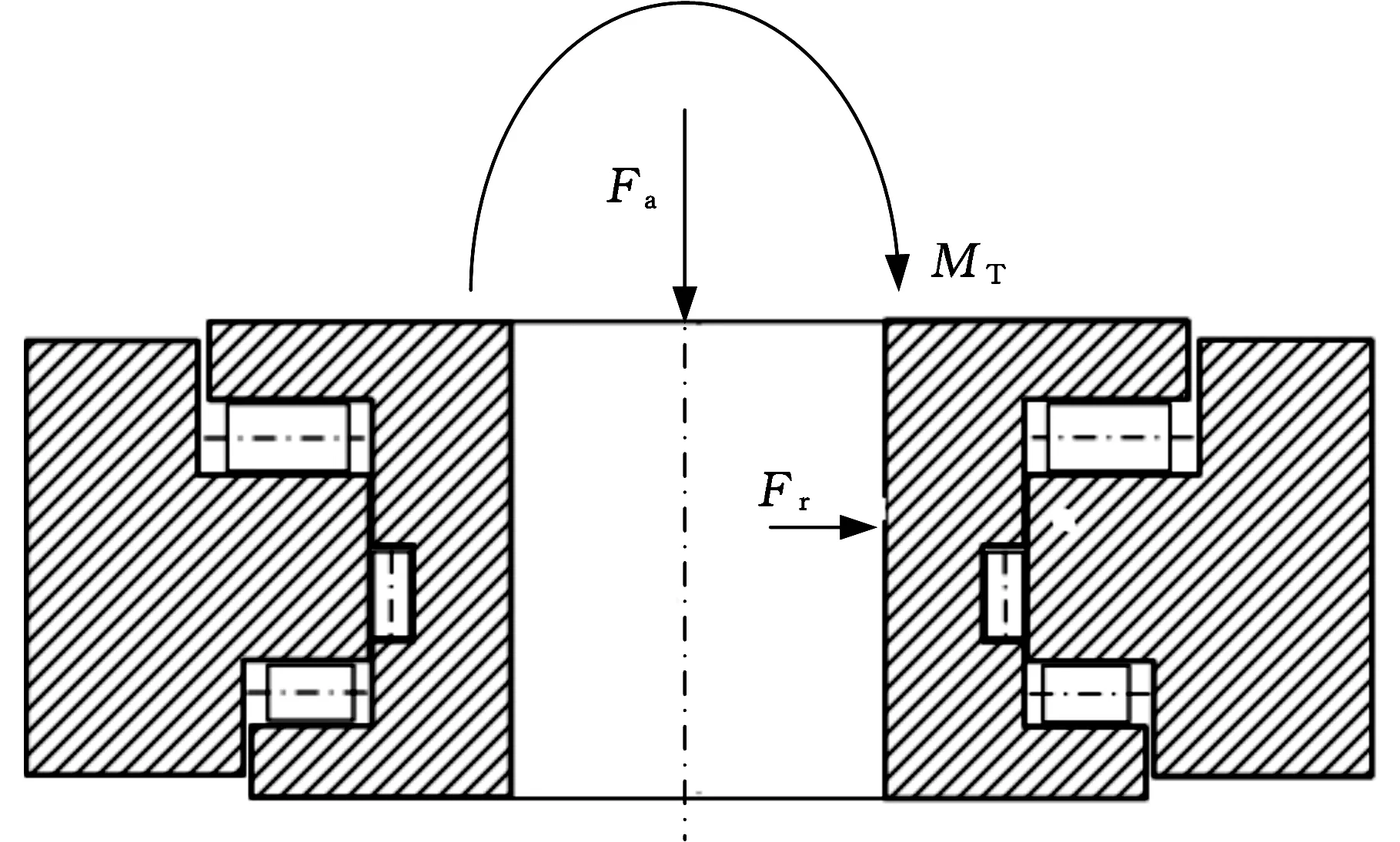
图2 回转支承受力简图Fig.2 External loads on a large roller slewing bearing
(1)
式中,n为滚柱个数;D0为滚道中心直径,mm。
2 接触变形及接触应力分布规律
2.1 接触变形沿滚柱轴向分布规律
三排柱回转支承中滚柱与滚道的线接触具有有限长度,接触变形及接触应力沿滚柱轴线方向分布并不均匀[18]。滚柱与滚道接触矩形的变形量为
(2)
(3)
式中,P为滚柱法向载荷,N;P1为滚柱中心处法向载荷集度,N/mm;a为滚柱中心处接触矩形半宽,mm;l为接触矩形半长,mm;d为滚柱直径,mm;E*为两物体当量弹性模量,MPa;E为弹性模量,MPa;μ为泊松比。
除去紧靠滚柱端头处,沿着滚柱的长度方向上的变形量与δ(0,0)之间有如下关系:
(4)
在紧靠滚柱端头处的变形量与δ(0,0)的关系式为
(5)
由式(2)~式(5)可得到滚柱与滚道沿接触方向变形量的变化规律。
2.2 接触应力沿滚柱轴向分布规律
计算滚柱与滚道的接触应力,需要知道其接触刚度,为简化计算,本文中假设沿滚柱轴向线接触刚度为常数。根据文献[20],线接触的弹性变形δk与法向载荷P之间有如下关系:
(6)
式中,le为滚柱有效接触长度,mm。
由式(6)可得到滚柱上单位长度法向载荷P1(0,y)与变形量δ的关系式为
(7)
式中,kl为滚柱与滚道的线接触刚度。
由式(2)~式(5)及式(7),可得出滚柱与滚道接触时,接触变形与接触应力沿滚柱轴向的变化规律。
3 滚柱与滚道接触区域应力场分析
3.1 法向载荷作用下应力场分析
通过第2节的分析得到了滚柱与滚道接触的法向载荷P1(0,y),则接触区半宽a1及接触区域压力分布p(x,y)可表示为[18]
(8)
(9)
(10)
式中,p0为最大接触应力,MPa;a1为法向载荷P1(0,y)作用下的接触半宽,mm。
由于滚柱与滚道的接触区尺寸远远小于滚柱的轴向长度,故可将柱式回转支承接触模型简化为平面应变问题。纯法向压力作用下接触区域应力场中,任意点(x,y,z)的应力分量如下[21]:
(11)
(12)
(13)
(14)
其中,m和n是辅助变量,表达式如下:
(15)
(16)
这里,m和n的符号分别与x和z的符号相同。
上述关于圆柱体接触应力场的求解公式只适用于纯法向载荷接触状态,但回转支承在实际工作状态下,滚柱与滚道的接触表面不可避免地会传递切向摩擦力,因此,需要考虑切向载荷作用下滚柱与滚道接触区域的应力场。
3.2 切向载荷作用下应力场分析
回转支承实际工作状态中滚动体与滚道之间不产生相对滑动,接触表面传递的切向摩擦力一般小于极限摩擦力,此处可假设滚柱与滚道的接触处于临界状态,该接触状态下切向摩擦力q(x,y)的分布可表示为
式中,fs为摩擦因数。
由于q(x,y)与p(x,y)成比例,由弹性理论可知,由切向力产生的应力与由法向力产生的应力之间有类似之处,它们的关系可表示为[18]
式中,q0为接触区中心处的最大切向力,q0=fsp0。
综上,q(x,y)单独作用下接触区内任意点(x,y,z)的应力分量可表示为
(17)
(18)
(19)
3.3 法向与切向力共同作用下应力解析
基于小变形及线弹性的前提,将上述两种状态下的各应力分量进行对应的线性叠加,可得到柱式回转支承中接触区域及滚道内部的各应力分量:
(20)
(21)
(22)
σy=μ(σx+σz)
(23)
3.4 接触区内部主应力及最大切应力
接触区内部任意一点的应力状态如图3所示,σy即为其中的一个主应力,其余两个主应力可根据应力状态理论求出。
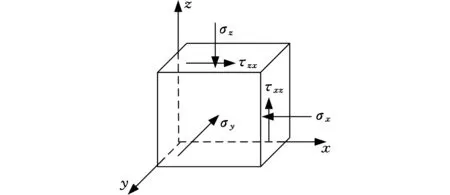
图3 点的应力状态示意图Fig.3 A given point of the stress state
根据应力状态分析中主应力计算公式:
(24)
将式(20)~式(23)计算所得到的应力分量代入式(24),即可得出其中两个主应力,至此接触区内部任意一点的三个主应力已全部求出,进而可求得Von Mises应力和最大切应力等。
4 计算结果与仿真验证
在上述理论分析的基础上,以131.32.2000.00Z型三排柱式回转支承为算例,建立了滚柱与滚道的接触有限元模型,以验证本文中解析解的合理性。计算所用的材料及载荷参数如下:弹性模量E=2.1×105MPa,泊松比μ=0.3,滚柱直径为32 mm,长度为31.3 mm,滚柱的最大法向载荷为103 400 N,摩擦因数为0.1。
4.1 有限元模型建立
滚柱与滚道均采用8节点solid185单元,接触区域网格大小控制为0.3 mm,单元总数目为263 850,滚柱与滚道的接触行为通过接触单元Conta174和目标单元Targe170来进行模拟,有限元模型如图4所示。本文中的约束及载荷处理方式如下:①对鼻圈上最左边缘的所有节点进行全约束,在滚柱与鼻圈的对称面上施加对称约束;②在滚柱上表面施加轴向载荷,并耦合其上所有节点的轴向自由度。

(a)1/4模型 (b)接触对图4 滚柱-滚道接触的1/4有限元模型Fig.4 1/4th FEM-model of roller-raceway contact
4.2 结果比较与讨论
图5和图6分别给出了接触中心(x=0,z=0)处的接触应力及Von Mises应力沿滚柱轴向的变化曲线。图5和图6显示,本文基于非理想Hertz接触计算方法获得的接触应力及Von Mises应力与有限元解基本一致,滚柱中心及滚柱端部的应力计算结果如表1所示。由表1可知,解析解与有限元解最大相对误差为6.6%,说明本文中的计算方法是有效的。
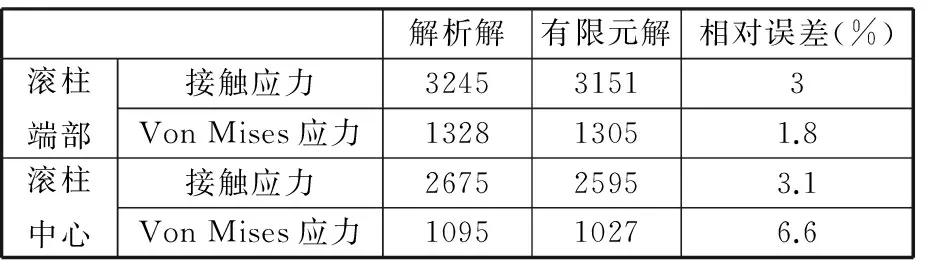
表1 滚柱-滚道接触计算结果
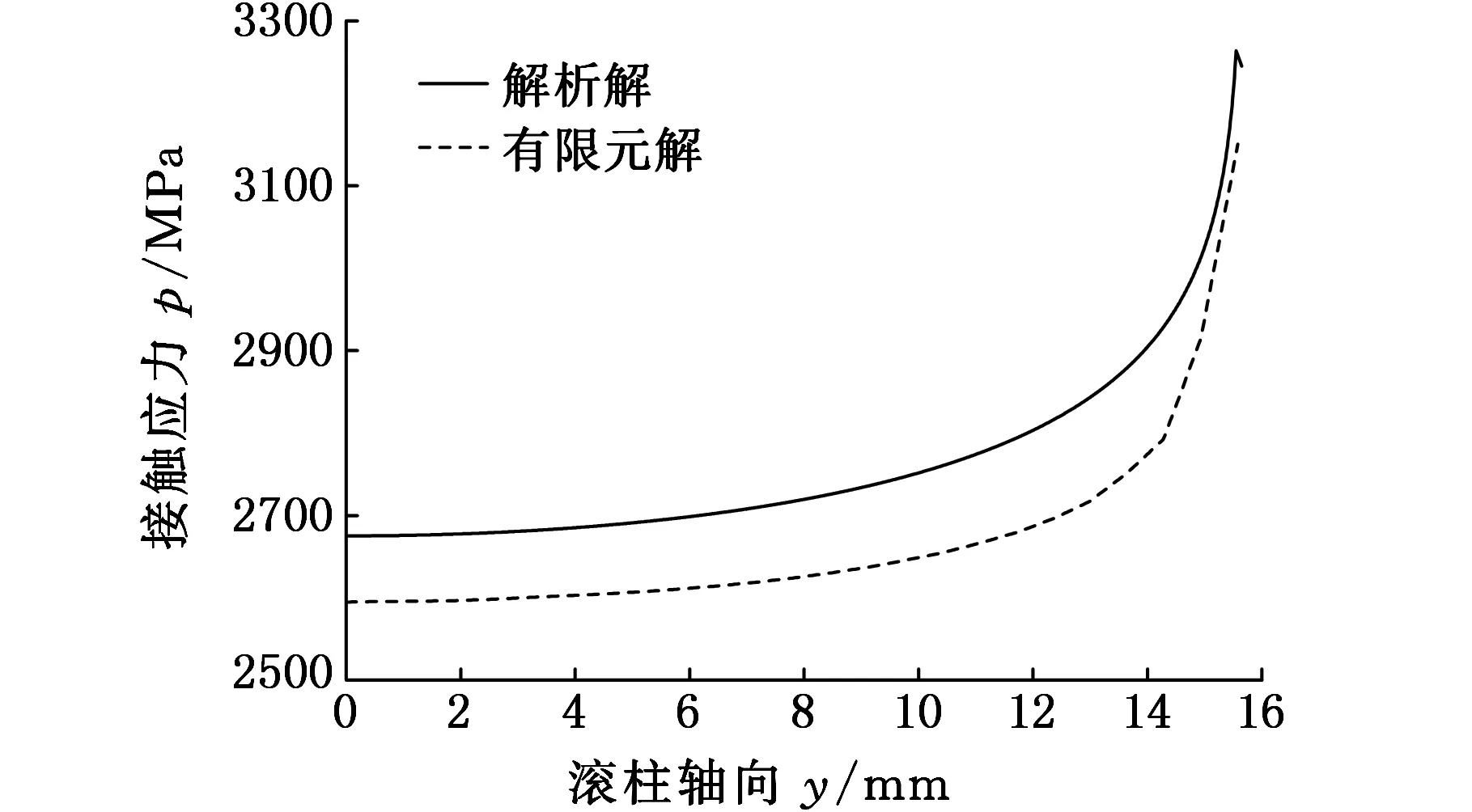
图5 接触应力沿滚柱轴向变化曲线Fig.5 Contact pressure distribution in y-direction
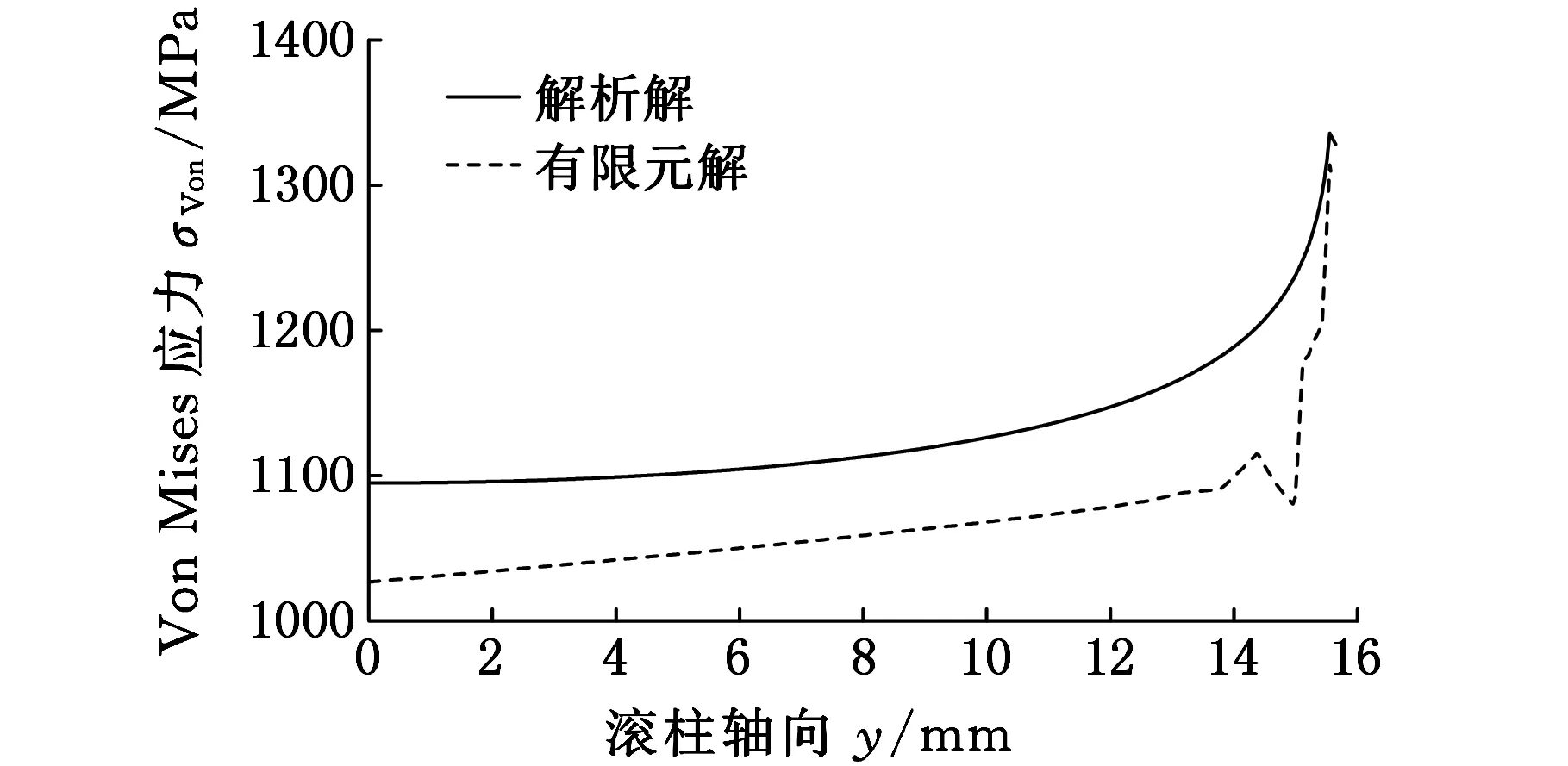
图6 Von Mises应力沿滚柱轴向变化曲线Fig.6 Von Mises stress distribution in y-direction
由图5、图6中的应力分布还可看出,沿着滚柱轴线方向应力分布并不均匀,滚柱端部区域的应力比其他区域的应力要大,而根据理想Hertz接触得出的最大接触应力为2754 MPa,Von Mises应力为1127 MPa,且沿滚柱轴线方向均匀分布,这与本文中根据非理想Hertz接触得到的解析解在除去滚柱端部外的其他区域是吻合的,但理想Hertz接触没有反映出滚柱端部区域的真实应力分布。本文中的解析解滚柱端部与中心接触应力相差约17.6%,Von Mises应力相差约21.3%;有限元解接触应力相差约17.5%,Von Mises应力相差约17.5%。由此可见,滚柱端部的应力与滚柱中心的应力差异不能忽略,它可能是引起滚道损坏的重要因素之一。
图7和图8分别给出了滚柱端部接触中心(x=0)处,滚道的Von Mises应力及最大切应力随深度z的变化曲线,由非理想Hertz接触得出的Von Mises应力最大值位于z=0.7a1处,大小为σVon=0.53p0,切应力最大值位于z=0.78a1处,大小为τmax=0.301p0。由图7和图8可看出,本文中所得出的非理想Hertz接触解析解与经典的理想Hertz接触解相比,滚道Von Mises应力及最大切应力随深度z的变化规律相似,均为由表面至滚道内部先逐渐增大至最大值,然后逐渐减小;但基于理想Hertz接触得到的应力在滚柱端部区域明显偏小,故对柱式回转支承应考虑滚柱与滚道接触的非理想特性。
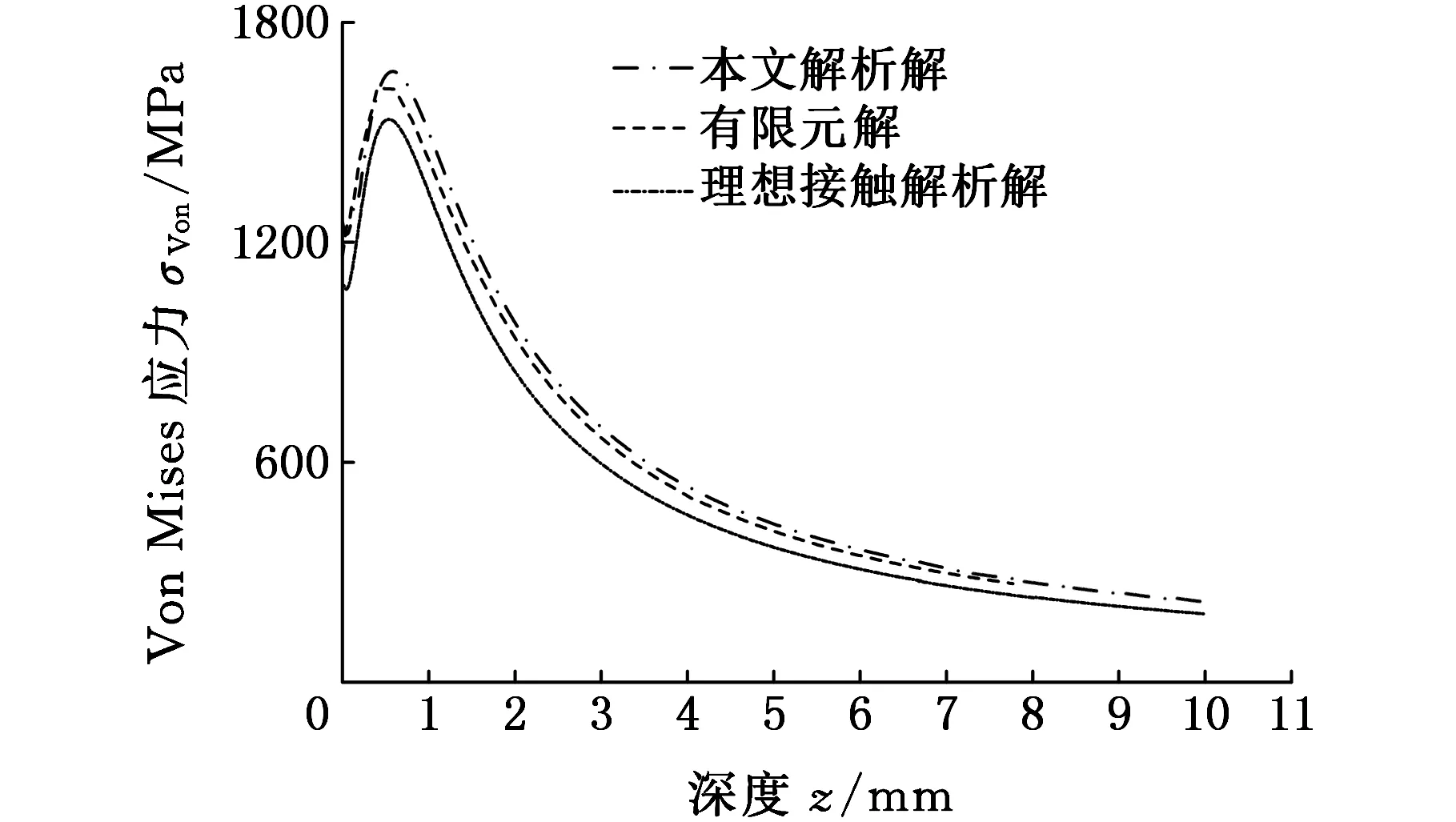
图7 滚道Von Mises应力随深度z变化曲线Fig.7 Raceway Von Mises stress distributionin z-direction
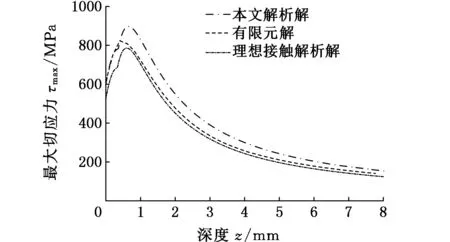
图8 滚道最大切应力随深度z变化曲线Fig.8 Raceway max shear stress distributionin z-direction
从图7和图8还可看出,回转支承在外载荷作用下,滚柱与滚道接触区的表面至潜层2 mm深度范围内,滚道表面及内部的Von Mises应力和切应力水平都较高,这正是造成回转支承在工作中,滚道产生剥落损坏的重要原因之一。滚道的剥落将导致整个回转支承的失效[8],因此,为保证回转支承工作的安全性及延长其使用寿命,回转支承所用材料在热处理过程中,应按照图7及图8中应力变化规律来保证滚道必须达到的硬度及淬硬层深度要求。
5 结论
(1)以三排柱式回转支承为研究对象,基于非理想Hertz接触分析,得出了滚柱与滚道之间的接触变形及接触应力沿滚柱轴向的分布规律,并研究了回转支承滚道内的应力场分布;同时,建立了三排柱式回转支承接触有限元模型,仿真结果与本文中基于非理想Hertz接触的解析解基本吻合,说明本文所采用的非理想Hertz接触分析得到的结果是有效的。
(2)基于理想Hertz接触得出的应力沿滚柱轴向均匀分布,不能反映出滚柱端部接触区域的应力大于中心接触区域的应力这一实际现象,若局部应力过大,则可能会引起滚道的损坏。因此,在回转支承运行过程中,考虑应力分布的不均匀性,采用非理想Hertz接触模型研究滚道的应力分布是十分必要的。
[1] 杜睿,吴志军. 单排球式回转支承的承载能力分析[J]. 机械设计与制造,2006(9):56-58.DURui,WUZhijun.AnalysisofLoadCapacityinaSingleRowSlewingBearing[J].MachineryDesign&Manufacture, 2006(9):56-58.
[2]AGUIRREBEITIAJ,ABASOLOM,AVILÉSR,etal.TheoreticalCalculationofGeneralStaticLoad-carryingCapacityfortheDesignandSelectionofThreeRowRollerSlewingBearings[J].Mechanism&MachineTheory, 2012, 48(1):52-61.
[3]KANIAL.ModellingofRollersinCalculationofSlewingBearingwiththeUseofFiniteElements[J].MechanismandMachineTheory,2006,41:1359-1376.
[4]KIMKH,SUKHG,HUHMY.DevelopmentoftheProfileRingRollingProcessforLargeSlewingRingsofAlloySteels[J].JournalofMaterialsProcessingTechnology,2007,187/188:730-733.
[5] 徐立民,陈卓. 回转支承[M].合肥:安徽科学技术出版社,1988:1-5.XULimin,CHENZhuo.SlewingBearing[M].Hefei:AnhuiScienceandTechnologyPress,1988:1-5.
[6] 汤卫斌,孙玉贤. 回转支承技术及行业发展概况[J]. 工程机械,1999,30(9):27-29.TANGWeibin,SUNYuxian.SlewingBearingTechniqueandSituationofItsIndustryDevelopment[J].ConstructionMachineryandEquipment,1999,30(9):27-29.
[7] 赵先琼,刘义伦,洪元. 回转支承构件牵引滚动接触应力解析[J]. 计算力学学报,2009,26(6):966-972.ZHAOXiaoqiong,LIUYilun,HONGYuan.ContactStressAnslysisofRotary-supportComponentunderTractiveRollingContact[J].ChineseJournalofComputationalMechanics,2009,26(6):966-972.
[8] 侯宁. 影响回转支承承载能力的四个参数[J]. 建筑机械,2002(1):21-22.HOUNing.TheFourParametersImpactofSlewingBearingCapacity[J].ConstructionMachinery,2002(1):21-22.
[9] 王燕霜,袁倩倩. 负游隙对特大型双排四点接触球轴承载荷分布的影响[J]. 机械工程学报,2012,48(21):110-115.WANGYanshuang,YUANQianqian.InfluenceofNegativeClearanceonLoadDistributionsofLarge-sizeDoubleRowFour-point-contactBallBearings[J].JournalofMechanicalEngineering,2012,48(21):110-115.
[10] 王思明. 风力发电机变桨轴承微动磨损研究[D]. 成都:西南交通大学,2007.WANGSiming.StudyonFrettingWearforWindTurbingPitchBearing[D].Chengdu:SouthwestJiaotongUniversity,2007.
[11]AMASORRAINJI,SAGARTZAZUX,DAMINJ.LoadDistributioninaFourContact-pointSlewingBearing[J].Mechanism&MachineTheory, 2003, 38(6):479-496.
[12]POTONIKR,GÖNCZP,GLODEŽS.StaticCapacityofaLargeDoubleRowSlewingBallBearingwithPredefinedIrregularGeometry[J].Mechanism&MachineTheory, 2013, 64(6):67-79.
[13]GÖNCZP,DROBNEM,GLODEŽS.ComputationalModelforDeterminationofDynamicLoadCapacityofLargeThree-rowRollerSlewingBearings[J].EngineeringFailureAnalysis, 2013, 32(9):44-53.
[14]GÖNCZP,POTOFINIKR,GLODEŽS,etal.LoadCapacityofaThree-rowRollerSlewingBearingRaceway[J].ProcediaEngineering, 2011, 10:1196-1201.
[15]GÖNCZP,POTONIKR,GLODEŽS.ComputationalModelforDeterminationofStaticLoadCapacityofThree-rowRollerSlewingBearingswithArbitraryClearancesandPredefinedRacewayDeformations[J].InternationalJournalofMechanicalSciences, 2013, 73(4):82-92.
[16]KANIAL,KRYNKEM,MAZANEKE.ACatalogueCapacityofSlewingBearings[J].Mechanism&MachineTheory, 2012, 58:29-45.
[17]KANIAL.ModellingofRollersinCalculationofSlewingBearingwiththeUseofFiniteElements[J].Mechanism&MachineTheory, 2006, 41(11):1359-1376.
[18]JOHNSONKL.ContactMechanics[M].London:PressSyndicateoftheUniversityofCambridge, 1985:27-29.
[19] 何西泠. 回转支承装置的摩擦阻力矩[J]. 中国工程机械学报,2006,4(2):183-186.HEXiling.FrictionResistanceMomentSlewingRing[J].ChineseJournalofConstructionMachinery,2006,4(2):183-186.
[20] 埃斯曼P,哈斯巴根L,韦根持K. 滚动轴承设计与应用手册[M].刘家文,译. 武汉:华中工学院出版社,1985:82-83.ESCHMANNP,HASBARGENL,WEIGANDK.ManualRollingBearingDesignandApplication[M].TranslatedbyLIUJiawen.Wuhan:HuazhongInstituteofTechnologyPress, 1985:82-83.
[21]MCEWENE.StressesinElasticCylindersinContactalongaGeneratrix[J].PhilosophicalMagazine, 1949, 40(1):454-457.
(编辑 王旻玥)
Non-Hertz Contact Characteristics Anslysis of Three-row Roller Slewing Bearings
FENG Jianyou QI Xiaoli TONG Jinyu
School of Mechanical Engineering, Anhui University of Technology,Maanshan,Anhui, 243032
The traditional contact analysis methods of the rolls and raceways of three row roller slewing bearings were based on Hertz contact theory, but the actual contact behaviors of rollers and raceways were beyond the scope of the Hertz contact theory. Aiming at this problem, focusing on the non-Hertz roller and raceway contact characteristics, the variation laws of contact deformation and contact stress along the axial direction of the rollers were found. Combined with McEwen theory on the cylinder normal contact, the analytical formula of stress components in contact filed of rollers and raceways was deduced, and the relationship among the raceway failures and stresses were discussed. Finally, the roller and raceway contact finite element model was built. The simulation results show that the contact stress distribution and the analytical solution are consistent with each other, the results may be used to provide a reference for designing and manufacturing of three-row roller slewing bearings.
roller slewing bearing; non-Hertz contact; contact stress; stress distribution
2016-03-31
安徽省科技攻关项目(12010202026)
TH133
10.3969/j.issn.1004-132X.2017.04.004
冯建有,男,1981年生。安徽工业大学机械工程学院讲师。主要研究方向为机械强度及可靠性。E-mail:fengjy509@163.com。戚晓利,男,1975 年生。安徽工业大学机械工程学院副教授、博士。童靳于,女,1987年生。安徽工业大学机械工程学院实验师。
