考虑关节摩擦的3-UPS/PU并联机构模糊自适应滑模控制

张 达 原大宁 刘宏昭

西安理工大学机械与精密仪器工程学院,西安,710048

考虑关节摩擦的3-UPS/PU并联机构模糊自适应滑模控制

张 达 原大宁 刘宏昭

西安理工大学机械与精密仪器工程学院,西安,710048

为克服3-UPS/PU并联机构关节摩擦力突变现象带来的跟踪畸变问题，设计了一种模糊自适应滑模控制方法。首先在机构动平台工作空间内建立该机构的整体动力学模型。针对切换型滑模控制驱动力抖振以及自适应滑模控制(ASMC)对摩擦突变较敏感的不足，提出一种模糊自适应滑模控制(FASMC)方法，该方法以自适应理论为基础，可以在线估计包括摩擦在内的系统模型不确定项，自适应增益通过模糊逻辑系统实现了动态调整，相比ASMC可以更准确地逼近摩擦的变化情况，从而更有效地抑制摩擦力突变影响，增强了系统鲁棒性。由于无需依赖具体的摩擦模型以及简单的控制结构，FASMC适用于并联机构这类复杂不确定系统。仿真结果显示，所采取的控制方法能有效估计并克服机构摩擦干扰，提高了机构的控制精度，而且驱动力没有出现抖振现象。

3-UPS/PU并联机构；关节摩擦；动力学模型；自适应滑模；模糊逻辑

0 引言

少自由度并联机构因精度高、结构简单、成本低的优点受到广泛关注。本文的研究对象3-UPS/PU并联机构具有动平台位姿检测方便、机架尺寸小、刚度大、实现点位能力强的特点，这为其应用在切削加工或装配等领域提供了可行性。轨迹控制对于并联机构的应用非常重要，基于机构动力学模型的控制方法考虑到机构的动态特性，可有效提高运动精度。制约该方法的主要问题是机构模型存在不确定性，而关节摩擦是导致该问题的重要因素，尤其是当3-UPS/PU并联机构的关节换向时会导致摩擦力出现正负突变现象，造成系统跟踪发生畸变，严重影响控制品质，因此研究如何抑制3-UPS/PU并联机构摩擦突变对控制的影响具有重要意义。通常针对摩擦的控制方法是基于摩擦模型的补偿控制，分为固定模型补偿和自适应补偿。固定模型补偿在模型参数的优化选择上存在困难；自适应补偿的参数通过线性迭代估计确定[1]，比如文献[2-3]将摩擦模型作线性参数化处理再通过自适应律在线辨识模型参数，文献[4]基于LuGre模型设计观测器进行补偿。但摩擦模型还没有一个统一的标准，无法确定哪个模型更适合，因此依赖于某个摩擦模型来设计控制律有一定的局限性。在机器人领域广泛应用的滑模控制(sliding mode control，SMC)[5-6]由于具备实现简单、对扰动不敏感的特点，也被用于抑制机构关节摩擦干扰[7]。近年来更为流行的是通过智能算法如模糊[8-10]、神经网络[11]、模糊神经网络[12]等技术对机器人关节摩擦进行在线逼近。文献[8]利用模糊系统的非线性函数逼近性能来辨识摩擦，但控制律中存在获取不确定的界的问题。文献[12]采用模糊神经网络来辨识机器人的关节摩擦，但参数的取值与计算过程比较繁琐。以上文献都只给出了速度稳态时的控制效果，没有说明关节过零速时摩擦突变现象对机器人控制精度的影响，对此文献[13]采用常规观测器来补偿单自由度伺服系统过零速时摩擦滞-滑现象，但在并联机构控制方面考虑摩擦突变影响的研究文献目前还很少。

本文考虑了3-UPS/PU并联机构所有移动副的摩擦力影响，推导出了系统数学模型，以滑模控制为核心，对比分析了常规滑模控制和自适应滑模控制(adaptive sliding mode control，ASMC)的效果，并设计了一种模糊自适应滑模控制(fuzzy adaptive sliding mode control，FASMC)方法。

1 3-UPS/PU并联机构

1.1 结构与自由度

如图1所示，3-UPS/PU并联机构的基座和动平台之间由3条UPS驱动支链和1条PU从动支链连接，基座、动平台上3个铰点均为正三角形布置。在基座中心o建立静坐标系oxyz。驱动支链由基座虎克铰、缸体、移动副、推杆和球铰组成，缸体上由伺服电机带动滚珠丝杠，再驱动推杆伸缩，从而驱使动平台运动。PU从动支链起到约束作用，位于基座中心并垂直于基座，在其约束下，动平台只有3个自由度：绕着从动虎克铰(下文均用Uc表示)的动轴、定轴转动，分别用欧拉角α、β表示；动平台的o′点与Uc中心重合，并随从动支链沿z轴平动，用h表示o和o′之间距离。另外动平台平面中心m与Uc之间加长一段距离以扩大动平台的工作空间。

1.虎克铰 2.缸体 3.移动副 4.推杆 5.球铰6.动平台 7.基座图1 3-UPS/PU并联机构简图Fig.1 Diagram of 3-UPS/PU parallel mechanism

1.2 动平台位姿的检测

从动支链的并联机构由于动平台位姿检测困难，更多采用关节空间控制，但因此忽略了机构的耦合特性而影响控制效果，相比之下该机构采用PU从动支链的优点是动平台(即末端操作器)的位姿检测比较方便，无需运动学正解，更容易实现工作空间的闭环控制，其中动平台姿态参数可通过编码器检测从动虎克铰Uc的转角得到，在从动支链移动副安装光栅尺可检测动平台o′点沿z轴的位移参数，与使用陀螺仪、视觉技术等复杂软硬件相比，要更加简便，有利于该机构的推广应用和实现精密控制。

2 系统数学模型

2.1 机构雅可比矩阵

在静坐标系oxyz下推导并联机构各杆件的速度雅可比矩阵。将动平台的位姿参数作为系统广义坐标，记为q=(α,β,h)T。

动平台角速度为

(1)

以下以某条驱动支链为例来说明机构运动学，故变量中暂不出现下标。基于动平台的运动可得到球铰中心的速度：

(2)

式中,vS为动平台o′点沿z轴升降速度；n为Uc中心指向球铰中心的矢量;JS为球铰中心速度雅可比矩阵。

将vS投影到驱动支链轴向，得到驱动速度:

(3)

式中,c为沿驱动支链轴向的单位向量；JL为驱动速度雅可比矩阵对应第i条驱动支链的行向量。

驱动支链绕基座虎克铰转动，推杆还可沿其轴向伸缩，则基于驱动支链的运动可得出球铰中心的速度：

(4)

式中,ω为驱动支链角速度；l为驱动支链长度。

式(4)两边同时叉乘，经整理得

(5)

式中,Jω为驱动支链角速度雅可比矩阵。

推杆质心速度为

(6)

式中,ru为推杆质心到球铰中心的距离;Ju为推杆质心线速度雅可比矩阵。

2.2 机构动力学模型

常用的机构动力学建模方法有虚功原理法[14]、牛顿-欧拉法[15]、拉格朗日法[16]，其中虚功原理法只需分析系统主动力，不必考虑关节约束反力，推导过程简明，以下基于虚功原理建立3-UPS/PU并联机构的动力学模型。由虚功原理可知，机构所受主动力做的虚功之和为零，各主动力包括各杆件的惯性力(矩)、重力(矩)、作用在推杆上的驱动力、动平台所受负载和关节摩擦，在此考虑从动支链和各驱动支链移动副的摩擦。因此有

Wd+Wl+Wp+Wo=0

(7)

式中，Wl、Wu、Wp、Wo分别为缸体、推杆、从动支链、动平台上的主动力做的虚功。

根据各杆件的运动、受力情况分别计算虚功：

(8)

(9)

(10)

(11)

δl=JLδqδφ=Jωδqδφ=Jpδqδu=Juδq

z=(0,0,1)T

式中，下标i表示第i条驱动支链，i=1,2,3；δq为广义坐标的虚位移；δl为推杆沿其轴向的虚位移；δθ为驱动支链绕基座虎克铰转动的虚位移；δφ为动平台绕从动虎克铰Uc转动的虚位移；δφ为推杆质心在空间平动的虚位移；τ为螺母作用在推杆轴向的驱动力；FE∈R3×1为作用在动平台位姿方向的广义负载；md、ml、mp、mo分别为缸体、推杆、动平台、从动支链的质量；g为重力加速度；al为推杆沿轴向的线加速度；Rn为从Uc指向动平台质心的矢量；Rd为基座虎克铰中心指向缸体质心的矢量；Ed、El、Ep分别为缸体、推杆、动平台的惯性力矩;Id为缸体关于基座虎克铰中心的惯性张量;Il为推杆关于其质心的惯性张量;Ip为动平台关于o′点的惯性张量；fl、fo分别为驱动支链、从动支链移动副摩擦力。

相比传统的静态摩擦模型，LuGre摩擦模型由于考虑了动态特性，模拟精度高，将其引入并联机构，可以更真实地模拟系统的摩擦环节，对机构的高精度控制具有重要的意义。该摩擦模型可表示为

(12)

将式(8)～式(11)代入式(7)，各雅可比矩阵JL、Jω、Jp、Ju已在2.1节中推导得到，再消去δqT，最后整理得到3-UPS/PU机构关于广义坐标的动力学模型：

(13)

式中,M∈R3×3为系统惯性矩阵，对称正定且有界；C为向心力和科氏力系数矩阵；G为重力项；f为广义坐标下的各移动副摩擦力；FE∈R3×1为作用在动平台位姿方向的广义负载；τ为驱动力，τ=(τ1,τ2,τ3)T；J为力雅可比矩阵。

3 控制方法

本文以滑模控制作为基本控制方法并加以展开，控制目标是有效抑制3-UPS/PU并联机构摩擦、负载等干扰因素，使得机构动平台的实际轨迹能准确跟踪期望轨迹，并保持系统稳定。

3.1 滑模面

(14)

为使系统的跟踪误差在有限时间内收敛，定义Terminal滑模面[17]：

(15)

式中,λ∈R3×3是正定阵；a、b均为正奇数，ab。

设定辅助控制量：

(16)

(17)

为解决该问题，采用线性滑模面和Terminal滑模面结合的方法，由于控制律奇异性是误差e为零造成的，当e接近于零时，采用线性滑模面，以避免控制系统奇异性；当e较大时，则采用Terminal滑模面，以加快控制误差的收敛速度。因此将滑模面设计为复合型滑模面：

(18)

i=1,2,3

3.2 模型不确定性

考虑机构的物理参数误差、摩擦力和外负载之后，式(13)又可以表示为

(19)

式中,下标0表示由实测参数得到的模型名义值；下标Δ表示参数测量误差所致的建模误差。

将模型参数误差、未知的摩擦和负载集中起来作为总的不确定项，记为d，即

(20)

式中,d的第i个分量|di|≤bi，bi>0是上界值，i=1,2,3。

3.3 常规滑模控制

4）胸骨固定的钢丝以及一些特殊设计的、记忆合金的胸骨柄固定器：胸骨固定钢丝是钢制的，但胸骨固定以后，是非常牢固的，不易发生移位，因此1.5T以下磁共振检查是安全的。特殊类型的胸骨柄固定器，大多都是钛金属制造，所以磁共振检查不受限制。

SMC根据滑模面的正负状态进行来回切换以实现对不确定项d的抑制。控制律如下：

τ=J-T(F0-Ks-ρsgns)

(21)

为减弱滑模面切换造成的控制输入抖振，采用饱和函数替代式(21)中的符号函数，即

(22)

i=1,2,3

式中，ε为边界层厚度，ε>0。

从图2可看出，常规Terminal滑模控制存在驱动力抖振现象，虽然已经采用饱和函数减缓滑模面正负切换带来的抖振，但是当机构的移动副过零速导致摩擦突变时，驱动力还是会发生严重的抖振，这会降低驱动电机的使用寿命，因此该方法不利于实际应用。

(a)驱动杆1的驱动力

(b)驱动杆2的驱动力

(c)驱动杆3的驱动力图2 SMC驱动力曲线Fig.2 Curve of driving force with SMC

3.4 自适应滑模控制

式(21)的滑模控制需要准确预估不确定d的上界以满足稳定性，但在实际应用中由于工况的多变性与不可测性，d的上界值很难预先确定，另外驱动力抖振也制约了该方法的应用。自适应滑模控制由于可以对系统建模误差及扰动因素进行实时估计，从而省去了切换控制，是处理驱动力抖振问题的有效方法。自适应滑模控制律如下:

(23)

考虑到d会影响轨迹误差从而影响滑模面，故从滑模面的变化中可以反映出d的信息，由李雅普诺夫函数推导可以得出自适应律[18]。此处对于d的每个分量di分别给定如下自适应律：

(24)

i=1,2,3

式中，Λi是正的自适应增益。

由于自适应增益取得过大会造成控制输入饱和，因此这里的增益大小取为适中且固定。驱动力的仿真计算结果如图3所示，ASMC可以有效克服常规滑模控制驱动力抖振的问题，说明该控制方法具有可行性。考虑到动平台h方向的运动受到各移动副摩擦力突变的影响较大，此处就以h位移的控制误差曲线为例来说明控制效果。如图4所示，当摩擦不发生突变时，控制误差可以稳定在零附近;但是当摩擦力一旦突变，控制误差会显著增大，说明ASMC对机构的摩擦突变比较敏感，很难有效地抑制摩擦对机构运动的影响。

图3 ASMC驱动力曲线Fig.3 Curve of driving force with ASMC

图4 ASMC位移h的跟踪误差Fig.4 Tracking error in h direction with ASMC

3.5 模糊自适应滑模控制

(25)

模糊规则表示为如下if-then形式：

(a)输入系统

(b)输出系统图5 模糊系统的隶属度函数Fig.5 Membership function of fuzzy system

为考察所提出的控制器的平均性能，在此引入评价指标平均绝对值跟踪误差：

表1 模糊规则

图6 FASMC系统框图Fig.6 Framework of FASMC system

(26)

式中,Tm为运行时间。

从图7的驱动力曲线可以看出，驱动力随时间的变化总体上较为平稳，没有抖振现象，这是FASMC得以应用的前提条件。从图8的轨迹跟踪误差曲线可以看出，当摩擦突变时，FASMC与ASMC相比，其跟踪畸变有了明显改善。表2是两种控制方法的平均误差指标eITA的对比，在达到稳定状态后，采用ASMC时α、β、h的平均跟踪误差分别为0.041°、0.042°、0.628 mm，相比之下，采用FASMC时对应的误差值分别为0.025°、0.023°、0.156 mm，其平均控制精度要比ASMC更高。其原因是FASMC可以更有效地抑制摩擦力突变造成的影响。图9反映了不确定项d各个分量的逼近值与实际值的对比，可以看出模糊自适应律可以准确平稳地逼近时变的不确定项d的各个分量。

4 结论

(1)建立了3-UPS/PU并联机构在其工作空间的动力学模型，为基于模型的控制提供了参考。分析对比了常规Terminal滑模控制和自适应滑模控制的效果，发现常规滑模控制带有驱动力抖振问题，而传统自适应滑模控制在机构摩擦突变时有跟踪畸变现象。

(2)在传统自适应滑模控制的基础上做了改进，通过模糊控制器实现了自适应增益的动态调整，可以更精确地估计并补偿零速下的摩擦突变问题，提高了系统鲁棒性和动态品质。所设计的模糊自适应滑模控制与摩擦模型无关，物理实现简单，没有驱动力抖振现象，适用于3-UPS/PU机构这类多输入多输出的复杂不确定系统。

图7 FASMC驱动力曲线Fig.7 Diagram of driving force with FASMC

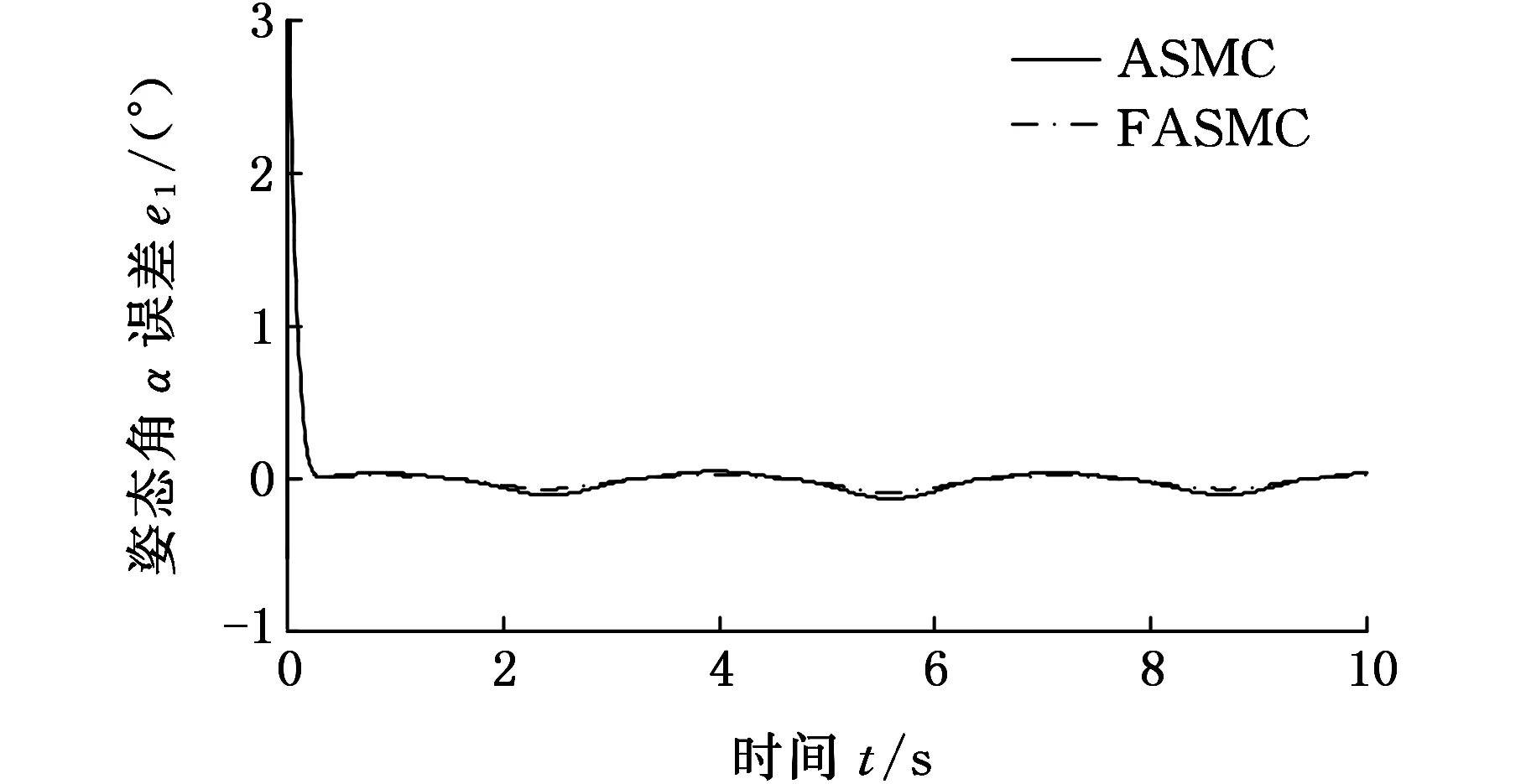
(a)姿态角α跟踪误差

(b)姿态角β跟踪误差

(c)位移h跟踪误差图8 FASMC的动平台轨迹跟踪误差Fig.8 Tracking error of platform with FASMC

姿态角α(°)姿态角β(°)位移h(mm)ASMC0.0410.0420.628FASMC0.0250.0230.156

(a)不确定项分量d1

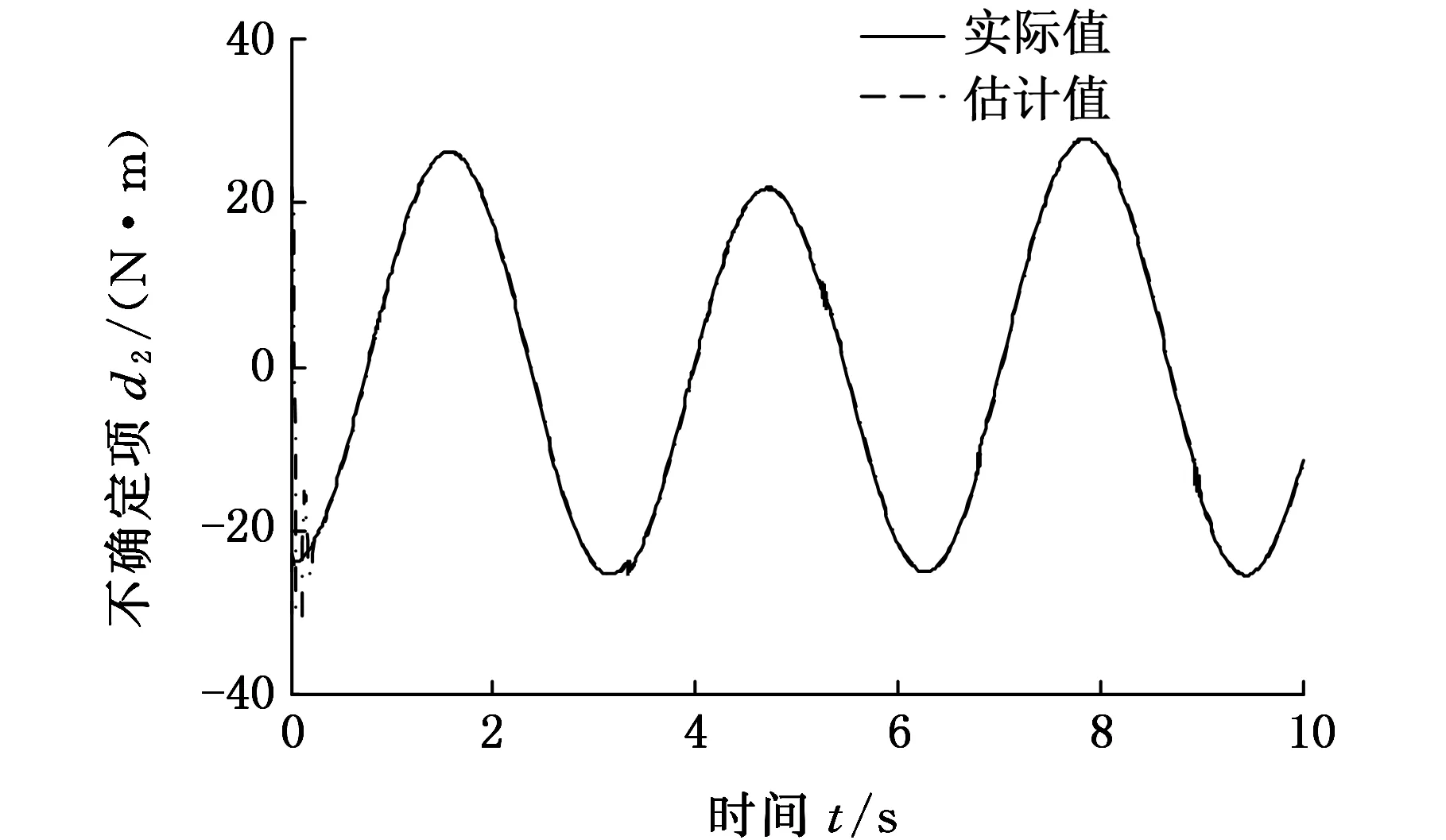
(b)不确定项分量d2

(c)不确定项分量d3图9 不确定项d的估计值与实际值Fig.9 Estimation value and actual value of uncertainty d

[1] 刘强. 高性能机械伺服系统运动控制技术综述[J]. 电机与控制学报, 2008, 12(5): 603-609. LIU Qiang. Survey on Motion Control Technologies of High Performance Mechanical Servo Systems[J]. Electric Machines and Control, 2008, 12(5): 603-609.

[2] 贺红林,占晓煌,刘文光,等.直接驱动机器人自适应-PD复合运动控制研究[J]. 农业机械学报, 2014, 45(5): 271-277. HE Honglin, ZHAN Xiaohuang, LIU Wenguang， et a1. Robot Control Using a Hybrid Controller Composed of an Adaptive Controller and a PD Controller[J]. Transactions of the Chinese Society for Agricultural Mechinery, 2014, 45(5): 271-277.

[3] MARTON L, LANTOS B. Control of Robotic Systems with Unknown Friction and Payload[J]. IEEE Transactions on Control Systems Technology, 2011, 19(6): 1534-1539.

[4] FREIDOVICH L, ROBERTSSON A, SHIRIAEV A. LuGre-model-based Friction Compensation[J]. IEEE Transactions on Control Systems Technology, 2010, 18(1): 194-200.

[5] ISLAM S, LIU X P. Robust Sliding Mode Control for Robot Manipulators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(6): 2444-2453.

[6] LI T S, HUANG Yuncheng. MIMO Adaptive Fuzzy Terminal Sliding-mode Controller for Robotic Manipulators[J]. Information Sciences, 2010, 180: 4641-4660.

[7] 季晔, 刘宏昭, 原大宁. 含驱动摩擦的四自由度并联机构动力学分析[J]. 中国机械工程, 2012, 23(8): 910-914. JI Ye, LIU Hongzhao, YUAN Daning . Dynamics Analysis of a Four-DoF Parallel Mechanism Including Driver Friction[J]. China Mechanical Engineering, 2012, 23(8): 910-914.

[8] 吴文祥，朱世强，王宣银，等. 基于摩擦模糊建模与补偿的机器人低速控制[J]. 电机与控制学报，2013，17(8): 70-77. WU Wenxiang, ZHU Shiqiang, Wang Xuanyin, et al. Slow Motion Control of Serial Robots with Friction Compensation Based on Fuzzy Logic System[J]. Electric Machines and Control, 2013, 17(8): 70-77.

[9] 王永富, 柴天佑. 机器人关节摩擦的自适应模糊补偿建模与控制[J]. 仪器仪表学报, 2006, 27(2): 186-190. WANG Yongfu, CHAI Tianyou. Compensation Modeling and Control on Robot Joint Friction Based on Adaptive Fuzzy Systems[J].Chinese Journal of Scientific Instrument, 2006, 27(2): 186-190.

[10] WANG Y F, WANG D H, CHAI T Y. Modeling and Control Compensation of Nonlinear Friction Using Adaptive Fuzzy Systems[J]. Mechanical Systems and Signal Processing , 2009, 23: 2445-2457.

[11] CILIZA M K, TOMIZUKAB M. Friction Modelling and Compensation for Motion Control Using Hybrid Neural Network Models[J]. Engineering Applications of Artificial Intelligence, 2007,20(7): 898-911.

[12] 徐智浩，李胜，张瑞雷,等.基于LuGre摩擦模型的机械臂模糊神经网络控制[J]. 控制与决策, 2014, 29(6): 1097-1102. XU Zhihao, LI Sheng, ZHANG Ruilei, et al. Fuzzy-neural-network Control for Robot Manipulators with LuGre Friction Model[J]. Control and Decision, 2014, 29(6): 1097-1102.

[13] 王毅, 何朕.伺服系统的摩擦补偿[J]. 电机与控制学报, 2013, 17(8): 107-112.WANGYi，HEZhen.FrictionCompensationforServoSystems[J].ElectricMachinesandControl, 2013, 17(8): 107-112.

[14]SOKOLOVA,XIROUCHAKISP.DynamicsAnalysisofa3-DOFParallelManipulatorwithR-P-SJointStructure[J].MechanismandMachineTheory, 2007, 42: 541-557.

[15]JANUSZF,MAREKW.OntheUniqueSolvabilityofaDirectDynamicsProblemforMechanismswithRedundantConstraintsandCoulombFrictioninJoints[J].MechanismandMachineTheory, 2011, 46: 312-334.

[16] 牛雪梅，高国琴，刘辛军,等. 三自由度驱动冗余并联机构动力学建模与试验[J]. 农业工程学报，2013，29(16): 31-41.NIUXuemei,GAOGuoqin,LIUXinjun,etal.DynamicsModelingandExperimentsof3-DOFParallelMechanismwithActuationRedundancy[J].TransactionsoftheChineseSocietyofAgriculturalEngineering, 2013, 29(16): 31-41.

[17]MANZH，PALINSKIAP，WUHR,eta1.ARobustMIMOTerminalSlidingModeControlforRigidRoboticManipulators[J].IEEETransactionsonAutomaticControl，1994，39(12)：2464-2468.

[18]ZEINALIM,NOTASHL.AdaptiveSlidingModeControlwithUncertaintyEstimatorforRobotManipulators[J].MechanismandMachineTheory, 2010, 45: 80-90.

(编辑 王旻玥)

Adaptive Fuzzy Sliding Mode Control of 3-UPS/PU Parallel Mechanisms Including Joint Frictions

ZHANG Da YUAN Daning LIU Hongzhao

School of Mechanical and Precision Instrument Engineering,Xi’an University of Technology,Xi’an,710048

In order to overcome the tracking aberration caused by joint friction mutations of a 3-UPS/PU parallel mechanism, a fuzzy adaptive sliding mode control was proposed. Firstly, dynamics model of the mechanisms with respect to platform workspaces was constructed. Considering the traditional sliding mode control(SMC) had deficiency that driving force chattering and adaptive SMC(ASMC) was sensitive to friction mutations, a fuzzy ASMC(FASMC) was proposed, which might estimate and compensate the model uncertainty including joint friction based on adaptive theory. And the adaptive gains were adjusted dynamically by means of fuzzy logic system. Consequently, FASMC may estimate the frictions more accurately and restrain friction mutations more efficiently compared with ASMC, and the system robustness was improved. This control method did not need to rely on the friction model and had a simple structure, therefore it was suitable for complicated and uncertain systems such as parallel mechanisms. The simulation results show that the proposed control method may estimate and overcome the friction disturbances efficiently and improve the control precision, the chattering problems from driving torque are also resolved.

3-UPS/PU parallel mechanism; joint friction; dynamics model; adaptive sliding mode; fuzzy logic

2016-03-25

国家自然科学基金资助项目(51275404)；陕西高校省级重点实验室科研项目(2010JS080)

TH212；TH213.3

10.3969/j.issn.1004-132X.2017.04.003

张 达，男，1990年生。西安理工大学机械与精密仪器工程学院硕士研究生。主要研究方向为并联机构动力学建模及控制。E-mail：1837099973@qq.com。原大宁，女，1957年生。西安理工大学机械与精密仪器工程学院教授。刘宏昭，男，1954年生。西安理工大学机械与精密仪器工程学院教授、博士研究生导师。