OpenBUGS软件介绍及应用*
2017-03-09兰州大学公共卫生学院流行病与卫生统计学研究所730000
兰州大学公共卫生学院流行病与卫生统计学研究所(730000)
目前国内研究较多的是沈可[1]等人实现OpenBUGS软件在网状Meta分析中的应用,郑晓鸳[7]实现OpenBUGS软件在跳扩散Shibor模型中的应用。本文利用非条件Logisitic回归模型,研究少年儿童肥胖与胆固醇、甘油三酯、年龄和性别之间的关系,来实现OpenBUGS在非条件Logisitic回归中的应用。数据[8]见表2所示。
·计算机应用·
OpenBUGS软件介绍及应用*
兰州大学公共卫生学院流行病与卫生统计学研究所(730000)
张继巍 高文龙 秦天燕 刘建正 李学朝 拉扎提木拉提 李娟生△
OpenBUGS软件是在WinBUGS软件基础上研制的一款实现贝叶斯统计推断的工具软件,它是以MCMC(Markov Chain Monte Carlo)方法为基础,将所有未知或不确定的参数都视为随机变量,并对此种类型的概率模型进行求解[1]。它广泛地应用于医学、经济学、生命科学、心理学、社会科学等多个领域[1-4]。目前已经更新到OpenBUGS3.2.3版本,可以从其官网(http://www.openbugs.net/w/Downloads)上免费下载使用[5]。但是目前国内关于这款软件的应用报道比较少,对软件的基本情况也没有一个详细的介绍。因此,本文主要对该软件的功能和具体操作做一个简单的汇总和介绍,希望有兴趣的研究者能较快掌握这个软件,并起到抛砖引玉的作用。
OpenBUGS软件及特点
1.基本原理: 通过Gibbs 抽样和Metropolis算法,从完全条件概率分布中抽样,从而生成马尔科夫链,通过迭代,最终估计出模型的参数。
2.作用及过程:OpenBUGS 软件是通过Gibbs抽样和MCMC(Markov Chain Monte Carlo)方法从任意复杂模型的后验分布中产生样本,提供了一个有效的方法估计贝叶斯统计模型,极大地推进了贝叶斯的应用。因为它将所有的未知参数都视为随机变量,故可以方便的对许多缺失数据、异常数值、小样本资料和非参数模型及分布进行Gibbs抽样,实现Gibbs抽样的建模,并对其进行拟合和分析,最终得到模型参数的估计,并给出参数的Gibbs抽样动态图、核密度图、均数及其置信区间的变化图等,使抽样结果更直观、可靠。Gibbs抽样收敛后,还可以方便地得到参数后验分布的均数、标准差、95%置信区间和中位数等信息[6]。
3.分布类型:OpenBUGS中提供了29种常用的分布(用于指定似然函数和先验分布),主要有离散型单变量分布(discrete univariate distribution)、连续型单变量分布(continuous univariate distribution)、离散型多变量分布(discrete multivariate distribution)、连续型多变量分布(continuous multivariate distribution)等四种。其中最常用的有17种,如表1所示。

表1 OpenBUGS中的常用分布
4.基本操作
OpenBUGS的基本操作主要包括Doodle、Model、Attributes、Update、Inference、Info、Stats、DIC和Log等命令。
(1)Doodle:用于构建Doodle模型图,以节点、箭头和平板的方式出现。
(2)Model:通过Specificaion用于对模型进行校验,包括模型的检查、数据的加载、编译和初始值的生成。
(3)Attributes:用于改变所选文本的字体、格式、字体的大小和颜色等。
(4)Update:用于对Doodle模型进行迭代,可以设置迭代的次数和步长。
(5)Inference:用于指定想要考察的变量和迭代计算结果的输出。
(6)Info:用于获得节点和数据的信息。
(7)Stats:用于输出参数后验分布的统计量,比如均数、标准差、95%置信区间和中位数等。
(8)DIC:用于对多个待定模型的拟合优度进行比较选择,DIC值越小,模型的拟合度越好。
(9)Log:用于查看以上所有操作的具体信息。
应用实例
目前国内研究较多的是沈可[1]等人实现OpenBUGS软件在网状Meta分析中的应用,郑晓鸳[7]实现OpenBUGS软件在跳扩散Shibor模型中的应用。本文利用非条件Logisitic回归模型,研究少年儿童肥胖与胆固醇、甘油三酯、年龄和性别之间的关系,来实现OpenBUGS在非条件Logisitic回归中的应用。数据[8]见表2所示。

表2 少年儿童肥胖危险因素调查资料表
引入自变量X1[i],X2[i],X3[i],X4[i],其中




用ri表示第i组少年儿童肥胖的阳性数,ni表示第i组观察总例数,pi表示第i组儿童肥胖的阳性率,则有ri~Binomial(pi,ni)。
建立模型 logit(pi)=β0+β1X1[i]+β2X2[i]+β3X3[i]+β4X4[i]
其中beta用β表示;β0为常数项,又称截距;βj(j=1,2,3,4)为自变量Xj的偏回归系数;模型的参数β0,β1,β2,β3和β4已经给定了独立的“non-informative”先验分布。利用OpenBUGS软件建模和抽样,步骤如图1所示:
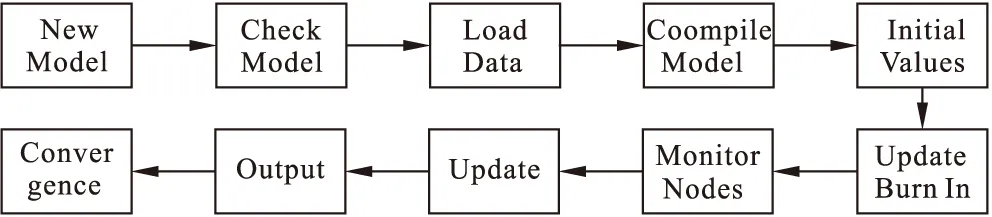
图1 OpenBUGS操作流程图
1.模型的建立(new model):通过 OpenBUGS软件进行Doodle建模,用来指定各参数的分布类型和逻辑关系,如图2所示:

图2 Doodle模型结构示意图
图2中每一个椭圆表示一个节点,矩形表示常数节点,单线箭头表示从父节点到随机型子节点,双线空心箭头表示从父节点到逻辑型子节点,边缘较粗的矩形为平板,其左下角的 “for(i IN 1:N)”表示for循环,实质是计算N个组的似然函数,从而获得整个数据的似然函数。
2.模型的检查(check model):模型设定完成后,点击Model下拉菜单Specification中的check model 按钮对模块进行检查,若检查无误,则软件窗口左下方会提示“Model is syntactically correct”,同时按钮load data和compile被激活,提示可以加载数据并进行编译。
3.数据的加载(load data)和编译(compile model):本例数据为
list(x1=c(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2),
x2=c(1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4,1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4),
x3=c(1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2,1,1,2,2),
x4=c(1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2),
r=c(8,1,0,0,12,8,1,12,5,9,2,4,22,4,0,1,7,0,2,0,12,7,2,5,2,7,2,1,4,3,0,0),
n=c(98,16,2,2,83,18,22,39,75,23,13,19,232,55,5,2,93,19,4,2,66,22,18,32,75,28,5,10,185,82,3,4),N=32)
将鼠标移到数据指示语“list”并选中,点击load data(加载数据)按钮,若左下方提示“data loaded”,则点击compile按钮进行编译,编译成功后,窗口底部左下方会提示“model compiled”,随即load-inits和gen inits按钮被激活 。
4.初始值的设定(initial values):本例初始值为
list(beta0=0,beta1=0,beta2=0,beta3=0,beta4=0)
与加载数据类似,选中指示语 “list”,点击load inits按钮加载(如果只产生一条链,此时窗口左下方出现“model is initialized”,gen inits按钮变灰,提示初始值设置完成;如果产生2条或2条以上的链,此时窗口左下方提示“initial values loaded but chain contains uninitialized variables”,继续点击gen load按钮,提示“initial values generated,model is initialized ”),初始值设定完成。
5.模型的退火(burn in):点击Inference下拉菜单中的Samples按钮,在弹出的 “Sample Monitor Tool” 对话框中的beg处输入相应的数字,如输入1000则表示抛去前1000次抽样以消除初始值对抽样的影响,实现对模型的退火,从1001次开始抽样。
6.变量的监控(monitor nodes):通过点击Inference下拉菜单中的samples,在弹出的对话框node处,添加自己想要观察的变量名(本例主要观察的变量为β0,β1,β2,β3,β4),逐一按set键确定,同时可以在percentiles下方的列表中选择给出的置信区间,默认为95%(val2.5pc,val97.5pc)置信区间。
7.模型的迭代(updates ):通过点击Model下拉菜单中的updates按钮对模型进行迭代运算,迭代的次数和步长可以自行设置。
8.结果的输出(output):通过Inference下拉菜单中Samples选项,在打开的“Sample Monitor Tool”对话框中的node处输入前面指定的观察参数,也可以直接输入“*”(“*”代表所有指定的参数),就可以获得各参数后验分布统计量,如图3~图8所示。
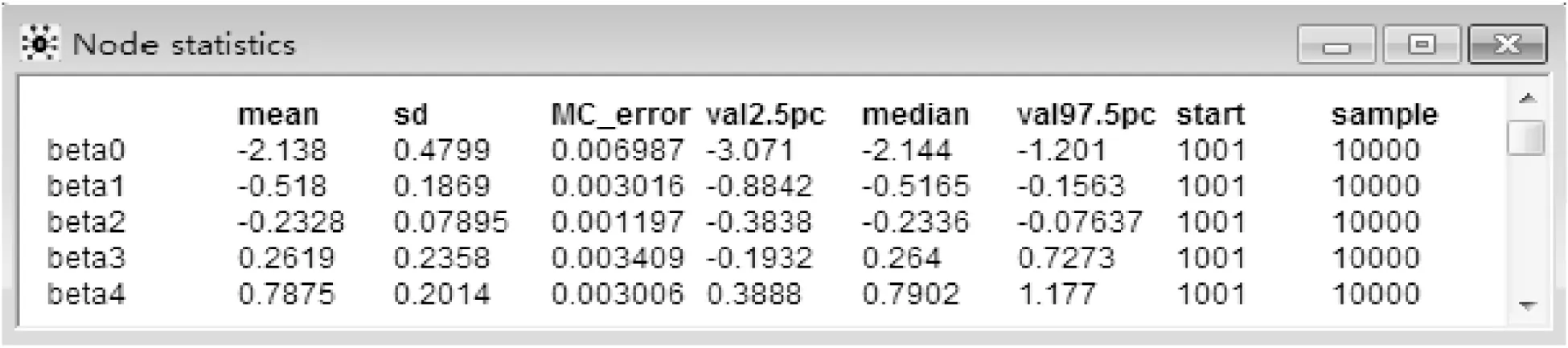
图3 各参数后验分布统计量
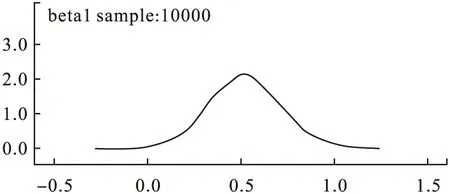
图4 核密度图
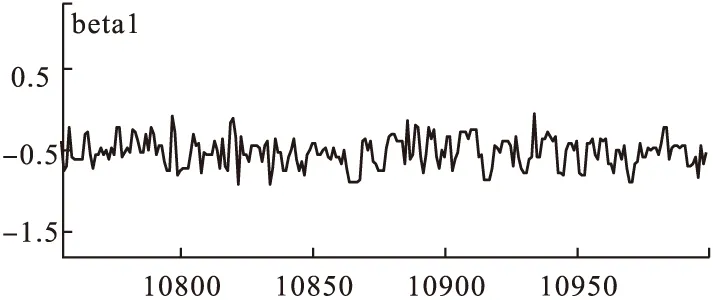
图5 迭代轨迹图
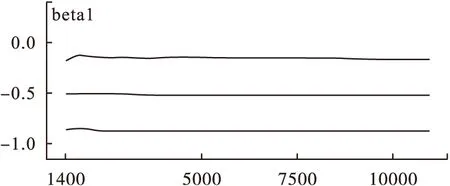
图6 分位数图
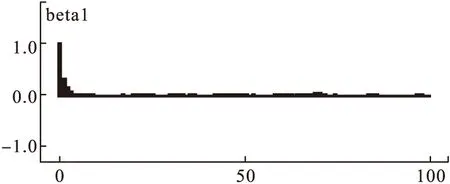
图7 自相关函数图
其中:MC_error表示蒙特卡罗模拟的误差,用来度量由模拟引起的参数均值的方差;val2.5pc和 val97.5pc分别表示中位数的95%置信区间的下限和上限;median表示中位数,通常比mean更稳定;start表示Gibbs抽样得起始点,本例抛去前1000次用于消除初始值对抽样的影响,从1001次后开始抽样;sample表示总共抽取的样本数。
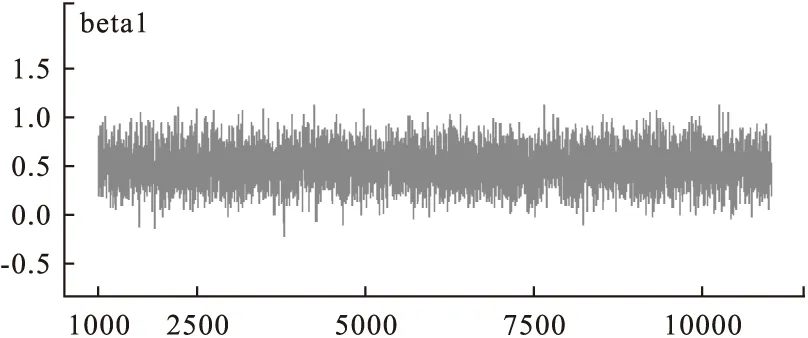
图8 迭代历史图
9.收敛性的判别(convergence):模型的收敛性可以通过观察遍历均值进行判断,在得到的链中每隔一段距离计算所观察参数的遍历均值,当这样算的均值稳定后,可认为模型收敛;也可以通过迭代轨迹图和迭代历史图来进行判断,当迭代轨迹和历史迭代趋于稳定,可以认为模型收敛[6]。 由图5,图8可知模型基本收敛,得到的回归方程为:Logit(pi)=-2.14-0.52X1-0.23X2+0.26X3+0.79X4。
讨 论
本文仅仅对OpenBUGS软件做了一个简单的介绍,通过实现OpenBUGS软件在非条件Logistic回归分析中的应用,使读者对该软件有一个初步的了解,并能掌握OpenBUGS软件的基本操作,变量的分布类型和作用以及熟悉OpenBUGS软件的操作流程。在运用该软件进行贝叶斯统计分析时,最重要的是对模型似然函数和参数先验分布的指定[9],这就要求使用者熟练掌握贝叶斯统计推断的理论知识,结合研究的具体内容,反复摸索。
OpenBUGS软件在克服WinBUGS缺点的基础上,对模型的代码和操作菜单做了相关优化和调整,使运行更加平稳,操作更为简单[1]。与其他贝叶斯分析软件(如BACC/BMA)相比,OpenBUGS软件的亮点就在于其具有很强的灵活性,能够使贝叶斯分析中复杂的数值计算简单化。但其在网状关系图、森林图等图形的绘制方面仍存在着不足[1],并且在代码建模过程中容易出现错误而不易被发现。目前,OpenBUGS还在更新和维护当中,其强大的数据分析能力,在不久的将来,会成为贝叶斯统计分析的主流软件。
[1]沈可,王芬,张超,等.应用OpenBUGS软件实现网状Meta分析.湖北医药学报,2013,32(6):476-479.
[2]Carroll R,Lawson AB,Faes C,et al.Comparing INLA and OpenBUGS for hierarchical Poisson modeling in disease mapping.Spatial and Spatio-temporal Epidemiology,2015,14(15):5-54.
[3]Lyle W,Konigsberg,Frankenberg.Bayes in Biological Anthropology.American Journal of Physical Anthropology,2013,152(57):153-184.
[4]Eitzel M,Battles J,York R,et al.Estimating tree growth from complex forest monitoring data.Ecological Applications,2013,23(6):1288-1296.
[5]OpenBUGS 3.2.3 user manual.
[6]孟海英,刘桂芬,罗天娥.Winbugs软件应用.中国卫生统计,2006,23(4):375-377.
[7]郑晓鸳.MCMC方法在跳扩散Shibor模型参数模拟中的应用.时代金融,2014,562(8):31-33.
[8]孙振球,徐勇勇,主编.医学统计学.第4版.北京:人民卫生出版社,2014,244-261.
[9]曾平,王婷,何鹏.非标准分布贝叶斯分析的WinBUGS软件实现.中国卫生统计,2012,29(4):614-617.
(责任编辑:郭海强)
教育部人文社会科学研究西部和边疆地区项目(项目批准号:15XJC910001)
△通信作者:李娟生,E-mail:ljsh@lzu.edu.cn
