壁挂式机载设备减振系统设计与分析

彭克侠，何海彬，杨 勇，胡 宇，符 浩

(北京航天控制仪器研究所， 北京 100094)

引 言

随着电子技术的不断发展，现代战争逐步向信息化、电子化作战转变，预警类特种飞机随之快速发展，其舱内设备的种类与数量不断增加，安装空间日趋紧张，因而对舱内设备的模块化和集成化要求也越来越高[1]。与此同时，现代战争环境对电子设备抵抗恶劣环境(主要包含电磁环境与力学环境)的能力也提出了较高要求。根据目前的统计数据，由振动冲击引起的电子系统的失效比例高达27%[2]。因此，设备减振系统设计的好坏在很大程度上影响着飞机整体的工作性能。

通过设计相应的转接支架，采用壁挂方式可以将舱内中小型电子设备集成于工作台，节省空间。但这种安装方式将使减振器承受切向预应力，与常规减振器设计时预应力为轴向的原则相反[1]，在振动过程中必然发生刚度耦合[3]。因此，有必要对这种安装方式的减振性能进行分析，为合理设计减振系统提供参考。

1 结构模型及有限元模型分析

1.1 结构模型分析

本文的研究对象为壁挂式机载设备减振系统，其中，设备采用壁挂式安装于工作台垂直面，如图1所示，减振器的安装方式如图2所示。

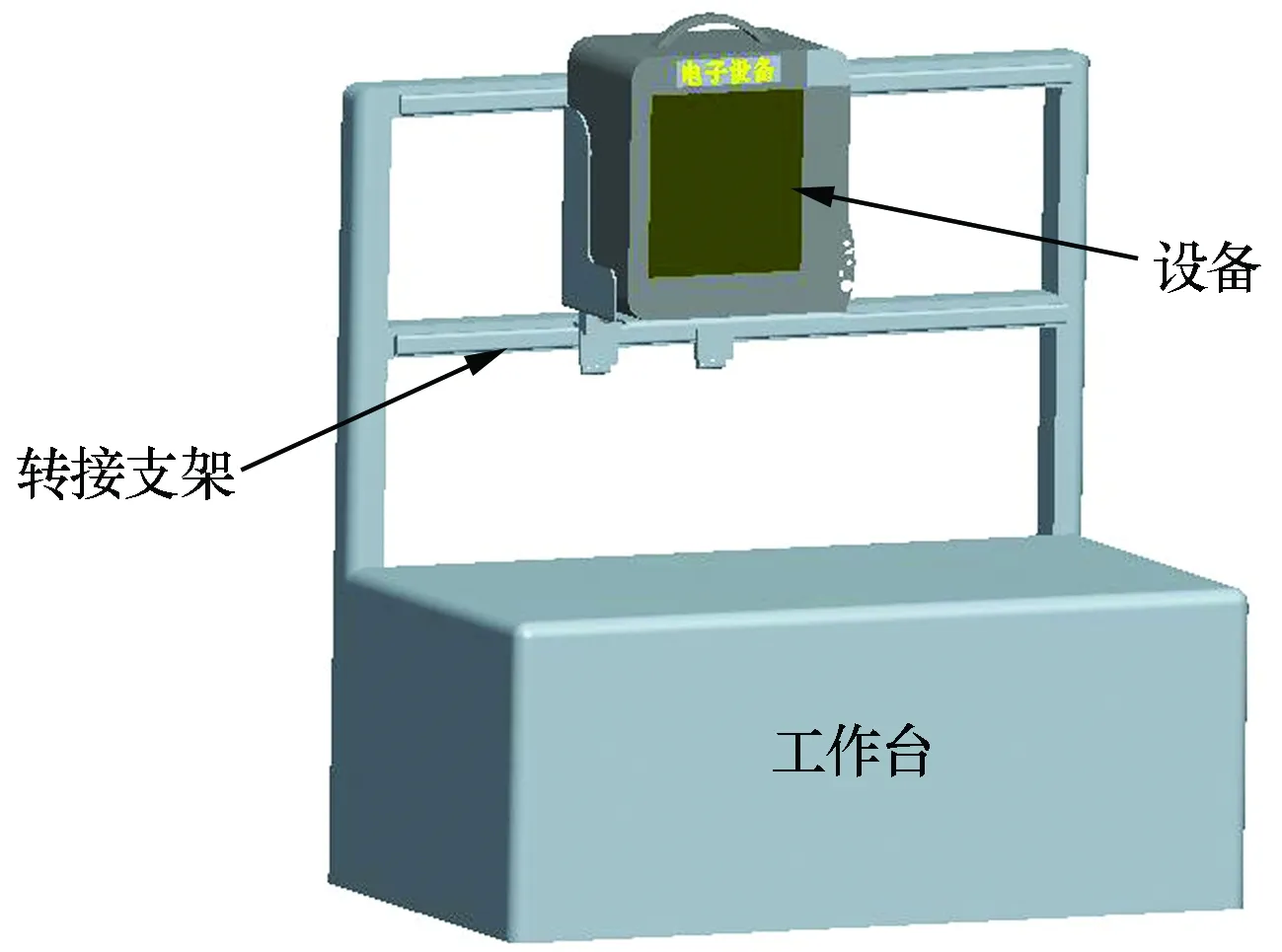
图1 设备安装方式

图2 减振器安装方式

1.2 转接支架有限元建模

壁挂式机载减振系统主要由转接支架、电子设备和减振器组件3部分组成。减振器组件为T型结构，几何模型简单。转接支架和电子设备的实际三维模型中包含圆角、斜角、螺钉孔和工艺孔等许多细微结构特征，对振动响应结果影响较小，但容易在有限元仿真分析过程中出现迭代发散。因此在保证支架整体结构刚度、强度等力学性能以及转动惯量、重心等质量特性参数基本不变的情况下，对转接支架和设备进行结构简化，并建立模型。同时为了尽可能得到质量较好、运算效率较高的六面体网格，对减振系统结构进行切割重组。最终的简化模型如图3所示，有限元模型如图4所示。

图3 简化模型

图4 有限元模型

2 基本理论

2.1 减振理论

根据阻尼振动理论及减振设计理论，可计算得到减振系统的传递率T(稳态响应幅值与激励幅值的无量纲比)[4]：

(1)

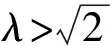
图5 减振器外形及作用方向

2.2 随机振动理论

随机振动是当系统受到随机激励时，系统激励和响应都是非确定的时间函数，不能用时间的确定性函数来描述[5]。但随机振动服从概率统计规律，因此其振动规律可以采用概率统计方法来描述[6]。通常描述随机振动响应的方式为功率谱密度函数。由力学基本理论[6]可知，动力学方程为：

(2)

响应功率谱密度函数矩阵为：

(3)

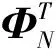
3 边界条件设置

3.1 基本假设

1)振动时设备位移较小，在仿真过程中，可以假设减振系统始终处于线性状态，不考虑非线性影响；

2)支架上下4个转接支架与工作台安装点均采用同一振动激励输入。

3.2 模型材料设置

壁挂式减振系统中转接支架与设备模型均采用铝合金材质，减振器套筒采用不锈钢材质。对于仿真过程中减振器材料的设置，可根据表1将系统阻尼比设为0.12，3种肖氏硬度的减振器弹性模量E可通过以下公式估计得出：

E= 3.57×105e0.034aN/m2

(4)

式中，a为橡胶常用肖氏硬度[2]。

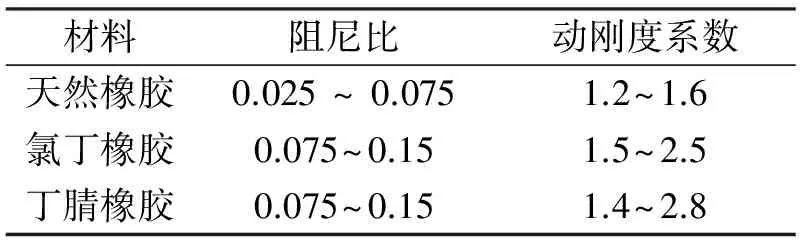
表1 橡胶材料阻尼比和动刚度系数

3.3 振动条件设置

壁挂式机载设备安装在螺旋桨飞机振动平台上，其振动环境主要包含飞机起飞、着陆、滑跑时跑道颠簸的激励、发动机振动激励、发动机喷气噪声激励、气流激励以及螺旋桨叶所带动的旋转压力场变化等多种影响因素综合产生的振动激励[7]。机舱内设备安装平台振动谱型[8]如图6所示，其中L0与设备安装位置有关。

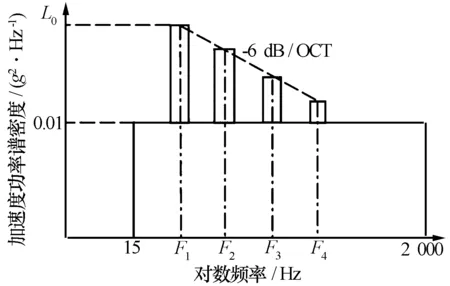
图6 螺旋桨飞机振动谱型

4 仿真运算与结果分析

通过选取不同肖氏硬度的减振器，完成壁挂式机载设备减振系统受X、Y、Z三向振动时的减振性能分析，并为减振器硬度选型提供依据。在仿真过程中，首先对减振系统进行预应力分析，得出在重力及减振器预位移作用下的动力学响应，并以此为初始条件进行预应力模态分析，得出减振系统在15～2 000 Hz内的各阶振型；然后基于模态叠加法，对减振系统进行随机振动分析，分别选取挂架与减振器直接相连的部位以及托盘与设备直接相连的部位作为监测点，其监测值即为壁挂式机载设备的输入激励和减振后的动态响应；最后通过仿真运算，得出挂架与机载设备上的振动响应曲线，通过曲线运行规律对比，完成对减振系统减振性能的分析研究。

4.1 X、Y、Z三向减振性能分析

在进行X、Y、Z三个方向上的随机振动仿真时，采用定量分析法，即受三向振动时，减振器均采用50°三向同性的丁腈橡胶减振器，轴向预位移为减振器轴向压缩量的10%，即0.5 mm。以此为初始条件，采用先预应力模态分析后振动响应分析的顺序，得出减振系统中挂架与机载设备分别受三向振动时的响应功率谱密度曲线，如图7和图8所示。

图7 X、Y、Z三向挂架响应功率谱曲线

根据壁挂式机载设备减振系统的结构形式，挂架为减振前的振动输入端，设备为输出端。由此壁挂式机载减振系统的减振效率即为设备、挂架振动量级差值与挂架振动量级的比值。结合图7和图8进行数据分析，可以得到壁挂式机载设备的减振效率，见表2。

表2 壁挂式机载设备受三向振动时的响应结果

从表2和图7所示的挂架在3个方向上的振动响应曲线可以看出：X、Z方向上的响应与输入的螺旋桨飞机原始振动谱型基本一致，而Y方向上的响应曲线变化较大，振动放大较为严重。同时从响应曲线上的多处谐振峰可以分析得出，Y方向上转接支架的结构形式对挂架的振动响应特性影响较为明显。综上所述，由于挂架在振动过程中发生共振，壁挂式机载设备转接支架在Y方向的减振响应情况较为复杂，振动环境更为苛刻。

从表2和图8中机载设备受各向振动时的响应量级可以看出：X、Z方向上的振动量级相近，Y方向上量级偏大，即在输入相同振动激励时，X、Z方向上设备所承受的振动量级低于Y方向，从而可以判定，设备在Y方向上所处的振动环境最为恶劣。根据受不同方向振动时设备的响应量级(RMS)，可计算得出X、Z方向上减振效率为74.9%，Y方向上的减振效率为67.3%，减振器在X、Z方向的减振效率高于Y方向的减振效率。

4.2 减振器硬度对减振性能的影响

由于转接支架受Y向振动时的减振响应情况相对于X、Z方向更为复杂，因此为了优化减振系统的设计，此处重点对受Y向振动时的响应情况进行分析研究。基于控制变量法，减振系统保持除减振器硬度外的其他力学参数不变，振动方向均为Y向，减振器分别选取40°、50°、60°三种不同硬度进行仿真分析。经仿真，减振系统在3种硬度条件下，挂架与设备上的振动响应功率谱密度曲线分别如图9和图10所示。

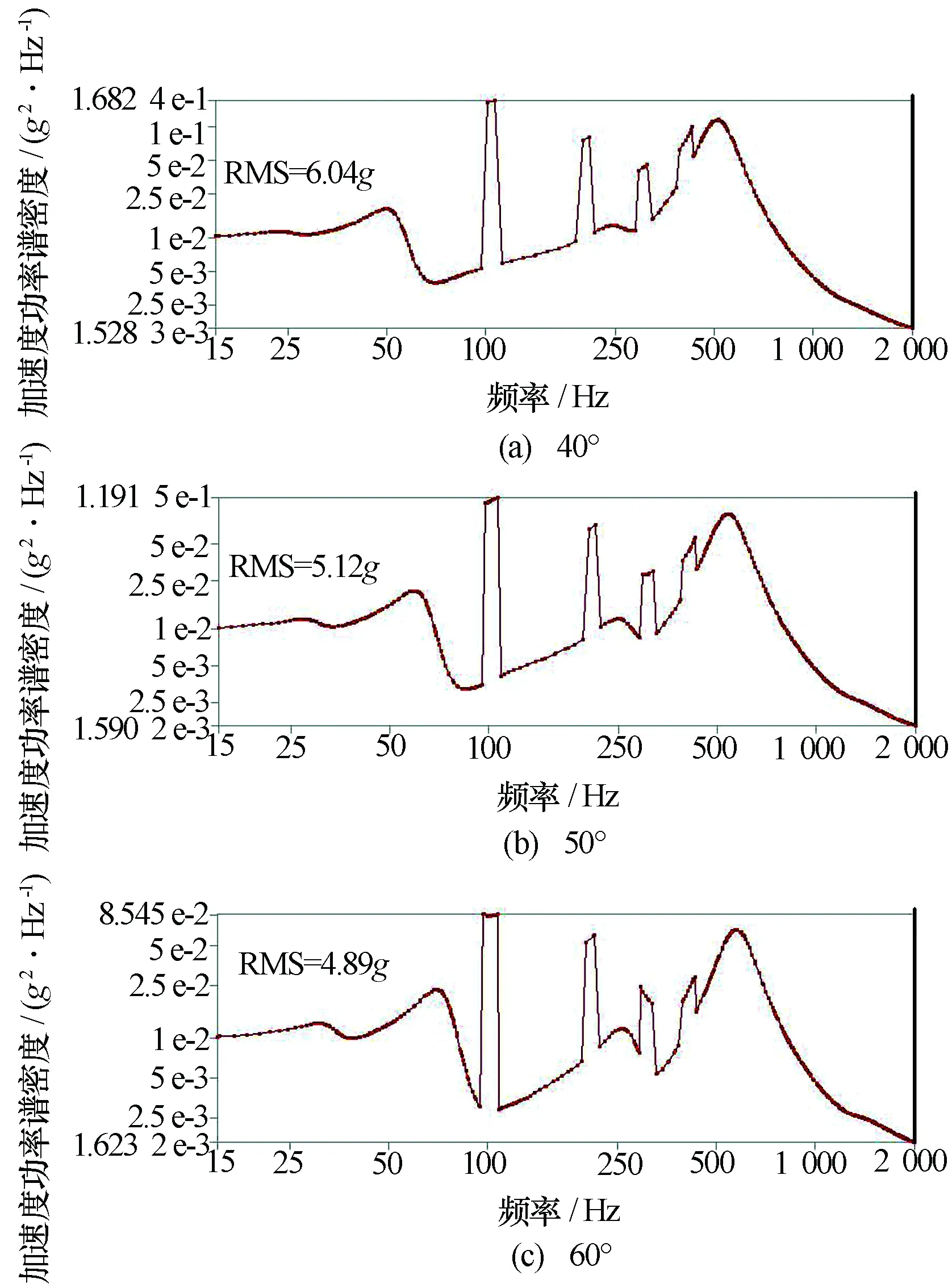
图9 40°、50°、60°减振器挂架振动功率谱曲线

图10 40°、50°、60°减振器托盘振动功率谱曲线

对图9和图10的数据进行分析处理，可得到壁挂式机载设备减振系统采用3种硬度减振器时的振动响应结果，见表3。

表3 壁挂式机载设备不同硬度振动响应结果

对图9和图10所示的3种硬度减振器的响应曲线规律进行对比发现：在减振系统结构形式相同的条件下，采用不同硬度减振器时，对应响应曲线的谐振点数量相同，曲线规律基本一致，但谐振频率有所不同。根据挂架与设备的振动量级(RMS)可计算得出：单纯考虑减振器效率时，40°减振效率为68.9%，50°为67.3%，60°为45.4%。随着减振器硬度升高，减振效率降低，并且减振器硬度越大，其减振效率降低越快，这与传统减振理论一致。

从图9所示的采用不同硬度减振器时减振系统在挂架部位的响应量级(RMS)可以看出，随着减振器硬度的升高，挂架响应量级反而降低。也就是说，虽然减振器硬度越大，减振效率越低，但由于挂架部位作为减振器的振动激励输入端，其振动量级随硬度降低而放大，两种规律叠加，最终导致整体设备转接支架减振效率在50°时振动响应量级最低。同时，从图10所示的采用不同硬度减振器的减振系统在托盘位置的振动量级(RMS)可以看出，减振器硬度为50°时设备的响应量级最低，40°其次，60°最低。

对减振系统振动响应功率谱密度曲线进行对比分析发现，设备整体转接支架减振效率复杂多变的关键原因是挂架受Y方向振动时的响应规律与减振器的减振规律正好相反。挂架受Y向振动时的响应规律之所以与减振器的减振规律正好相反，其原因是挂架在Y方向的刚度不强，自身可以等效为一组减振器，与其后连接的橡胶减振器形成多级减振形式。因此在后期减振设计过程中，需综合考虑挂架的刚度和减振器的硬度。

5 结束语

通过对减振器受X、Y、Z三向振动时的减振性能进行的仿真分析发现，减振器在X、Z方向的减振效率高于Y方向，X、Z方向上的曲线值与输入的螺旋桨飞机振动谱型基本一致，而Y方向上的功率谱曲线变化较大，减振响应情况较为复杂；通过对受Y向振动时不同减振器硬度对壁挂式机载设备减振性能的影响进行的仿真分析发现，挂架部位作为减振器的振动激励输入端，其振动量级随硬度降低而放大，这与减振器两者相互叠加，致使转接支架的减振效率复杂多变。

挂架受Y向振动时的刚度不强，会与橡胶减振器构成多级减振系统。因此在进行减振设计过程中，需结合挂架刚度参数，完成减振器硬度选型，为后期壁挂式机载设备减振设计提供参考。

[1] 季凡渝. 壁挂式隔振器弹性特性设计[J]. 电子机械工程, 2012, 28(6): 1-4.

[2] 邱成悌. 电子设备结构设计原理[M]. 南京: 东南大学出版社, 2001.

[3] 任娟. 减振器布局和跨度对捷联惯组振动的影响[J]. 导航与控制, 2015, 14(5): 105-106.

[4] 刘治虎. 某机载电子设备结构随机振动分析[J]. 航空计算技术, 2011, 41(4): 91-93.

[5] 杨斌. 电子设备的随机振动仿真分析[J]. 电子工艺技术, 2013, 34(5): 299-302.

[6] 杨文芳. 基于有限元分析的机载电子设备减振设计[J]. 振动与冲击, 2010, 29(5): 230-234.

[7] 李沅. 弹载制导系统抗振动与高过载冲击设计仿真[J]. 中北大学学报(自然科学版), 2014, 35(3): 293-297.

[8] 国防科学技术工业委员会. GJB 150.15A—2009军用设备环境试验方法[S]. 北京: 军标出版发行部, 2009.