机械产品装配精度可靠性评估软件开发与应用
2017-03-08罗宏亮胡祥涛陈帝江
罗宏亮,胡祥涛,苏 春,陈帝江
(1. 东南大学, 江苏 南京 211189; 2. 中国电子科技集团公司第三十八研究所, 安徽 合肥 230088)
引 言
飞机、雷达、工程机械、风力机等工程装备结构功能复杂,对装配精度提出了很高要求。因此,装配精度是机械产品的重要技术指标[1]。目前,装配精度主要依赖于设备的精度和相关人员的经验,通过测量和微调工艺手段来改善装配精度,尚缺少有效的精度分析理论与决策支持工具。
整机的装配精度由零件的制造误差和装配误差在装配工序中不断累积而形成。因此,装配精度可靠性评估应建立在装配误差传递累积规律分析的基础之上。根据装配对象不同,误差传递模型可以分为柔性薄板件的误差传递模型和刚性零部件的误差传递模型。柔性薄板件的装配误差传递研究常采用的方法包括误差流法[2]和状态空间法[3];刚性零部件的装配误差传递研究常采用的方法包括多体系统理论方法[4]、矢量法[5]等。在机械精度可靠性领域,文献[6]以曲柄滑块机构为研究对象,推导出弹性机构运动精度的可靠性数学模型,并采用响应面与重要抽样方法求解模型。文献[7]针对某大型龙门磨床,提出基于可靠性分析的精度分配方法,并采用响应面法计算精度可靠度。
目前,装配精度及其可靠性分析领域已形成较为丰富的研究成果,但是还缺少通用的装配精度可靠性理论。此外,现有的装配精度可靠性评估理论及流程复杂,增加了工程应用的难度。因此,开发通用的装配精度可靠性评估软件具有重要意义[8]。
本文结合某天线阵子模块装配精度评估的工程需求,考虑产品结构、尺寸、装配工序以及误差传递等因素,建立产品整机装配误差传递模型,评估装配精度可靠性。在理论模型的基础上,简化并固化分析流程,开发装配精度可靠性评估软件,并完成案例分析。
1 装配精度可靠性评估方法
1.1 装配误差状态空间模型
1.1.1 状态空间法
状态是指系统变量的一种有序组合,状态空间是指特定系统的状态集合。状态空间法是通过描述系统状态变量及其变化规律,开展系统分析和综合的一种方法。
对于多工序装配系统,其状态数与工序数对应,即每个工序对应一个状态变量。因此,可以利用状态空间模型描述多工序装配过程,计算装配误差,分析装配中误差的传递与累积过程,完成装配精度的计算与分析。
1.1.2 装配误差传递模型构建
由于装配误差是微小变动,可以采用小位移旋量(Small Displacement Torsor, SDT)描述误差源。旋量表示法可以转换为传递矩阵形式,通过状态空间坐标转换建立误差源与目标精度间的对应关系。
采用小位移旋量描述误差源时,将误差用沿x轴、y轴、z轴的位置误差矢量和绕x轴、y轴、z轴的方向误差矢量表示。例如:对于零件D,误差矢量包括零件上关键点d(一般选取零件装配表面的几何中心)沿各坐标轴的微小移动量以及绕各坐标轴的微小转动量,表达式为:
(1)
式中:D(d)为零件的位置误差矢量;D′为零件的方向误差矢量;ΔXd(D)、ΔYd(D)、ΔZd(D)分别是零件上点d沿x轴、y轴和z轴的微小移动量;Δα(D)、Δβ(D)、Δθ(D)分别表示零件绕x轴、y轴和z轴的微小转动量。
如图1所示,将装配过程视作一个系统,每个装配工序对应一个状态变量,该变量受到内部状态变量与外部输入变量的共同作用。本文将当前工序的总误差作为状态变量,制造误差作为内部状态变量,装配误差作为装配过程的外部输入变量,随着装配过程一同输出到下一道工序的状态变量,直至装配完成。
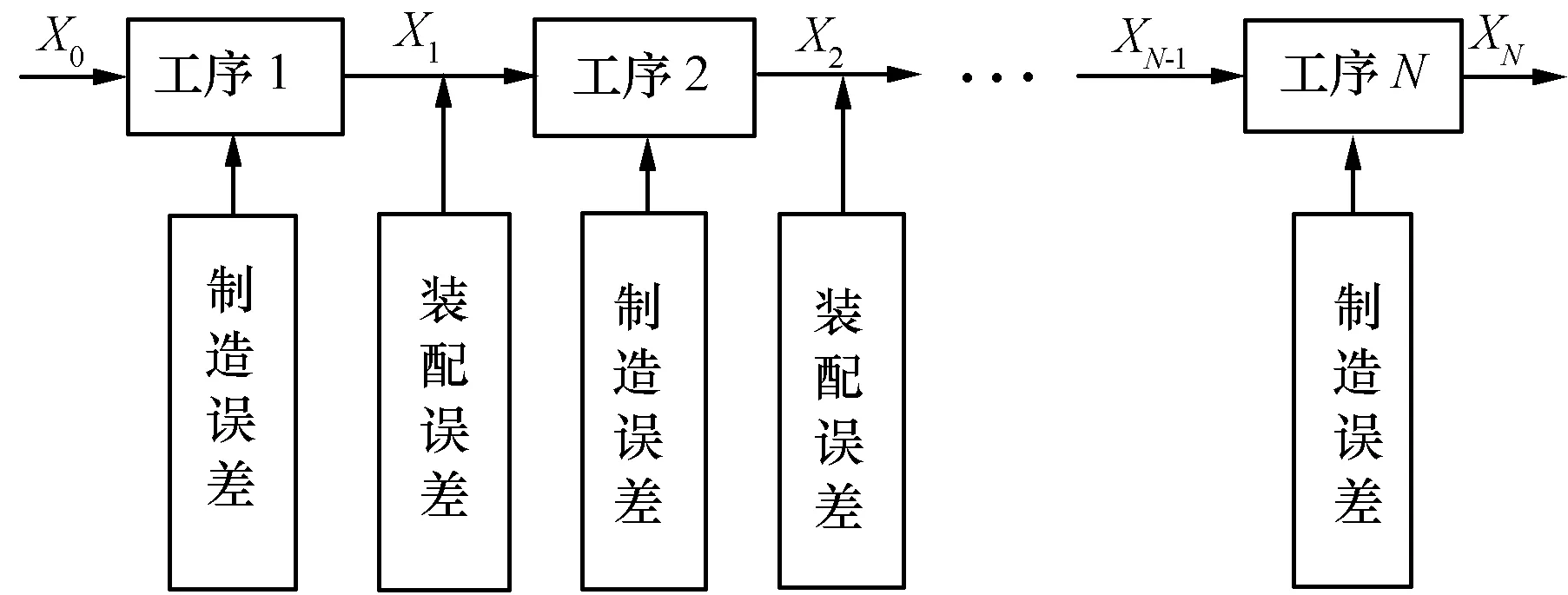
图1 装配误差传递示意图
因此,装配系统第i个装配工序的状态空间方程可以表示为:
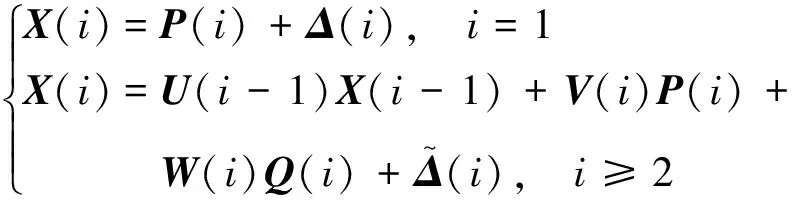
(2)
式中:X(i)是工序i(i=1, 2, … ,N)的误差状态矢量;U(i-1)表示工序i-1和工序i之间的误差传递矩阵;P(i)和Q(i)是工序i的制造误差矢量和装配误差矢量;V(i)和W(i)是控制矩阵,表示制造误差和装配误差对工序i误差的影响程度;Δ(i)和Δ(i)表示工序i的随机误差矢量。
1.1.3 关键点间误差传递矩阵
由式(1)可知,零件的误差矢量可以由零件上关键点的位置误差矢量和零件的方向误差矢量表示。当零件的方向误差Δα、Δβ、Δθ较小时,同一零件上除关键点A(xA,yA,zA)以外任意一点B(xB,yB,zB)的误差矢量与A点的误差矢量的关系可以由以下公式表示:
XB=GB,AXA
(3)
将GB,A定义为关键点间误差传递矩阵:
(4)
式中:Lx(B,A)=xB-xA;Ly(B,A)=yB-yA;Lz(B,A)=zB-zA。
对于相邻工序装配的2个零件,在配合面处分别选择关键点,建立误差传递矩阵,即可完成装配误差在工序间的传递。
与传统的位姿变换矩阵相比,本文构建的误差传递矩阵避免了多次建立零件坐标系的繁琐以及坐标系之间的复杂转化,可以高效地求解装配误差传递问题。
1.1.4 基于关键点误差传递矩阵的状态空间模型
结合关键点误差传递矩阵可以对状态空间方程进行简化,将式(2)转化为:
(5)
式中:G1是工序i-1与工序i的配合面关键点间的误差传递矩阵,表示工序间的误差转换关系;G2是工序i上制造误差的控制矩阵,通常为单位矩阵E;G3是工序i上装配误差的控制矩阵。
1.2 装配精度可靠性计算
装配精度可靠性是指产品在规定的装配条件下,实际装配精度能够满足设计精度要求的能力[9]。当以概率来度量时,即为装配精度可靠度。以s表示研究对象的实际装配精度,[s]表示目标装配精度,考虑零部件在加工、装配等环节的误差因素,以随机事件Ω表示实际装配精度s满足[s]的精度要求,则产品的装配精度可靠度可以表示为:
R=P(Ω)=P(s<[s] )
(6)
假设计算得到的实际装配精度为ΔS,目标装配精度范围为[ΔS-, ΔS+]。若ΔS满足ΔS-≤ΔS≤ΔS+,则认为装配精度符合要求,否则不符合要求。考虑到单次计算结果难以反映产品的真实装配精度,设共开展L次装配计算,其中符合精度要求的次数为M,则机械装配精度可靠度R可表示为:
(7)
1.3 装配精度可靠性分析基本步骤
综上所述,装配精度可靠性分析的步骤如下:
1)分析研究对象的结构组成和装配过程,确定装配工序和误差源。
2)设置精度目标。根据工艺设计文件或实际需要,明确研究对象的精度要求。
3)建立基准坐标系,确定装配过程中各零件的位置和方向。
4)选取关键点。确定各工序中用以描述误差传递和误差源的关键点。
5)绘制装配体各工序的误差传递流程图,建立装配过程的状态空间方程;得到装配过程中误差的变化趋势、误差范围及误差分布。
6)计算装配精度可靠度,评估最终装配精度可靠性。
2 装配精度可靠性评估软件开发
为固化繁琐的理论计算,便于装配精度计算方法的工程应用。本节基于上述方法并在对计算方法、过程做必要简化的基础上,开发了机械产品装配精度可靠性评估软件。
2.1 技术架构
装配精度可靠性评估软件包括数据层、工具层和应用层,系统架构如图2所示。数据层提供支撑装配精度可靠性评估软件所需的各类数据库,并用于管理可靠性评估过程数据和结果数据;工具层是指开发软件使用的主要工具,本软件开发以Visual Studio C++为核心,采用Qt开展界面设计,嵌入Creo接口用于三维模型显示,调用Matlab引擎完成数据计算,并以Office作为报表生成和相关数据管理的工具;应用层提供软件与用户交互的接口。
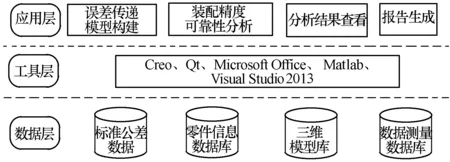
图2 装配精度可靠性评估软件架构
2.2 开发环境
2.2.1 三维模型环境配置
软件开发需要调用Creo 3.0。开展软件设计时,加载“QAxWidget”控件,在该控件中选择“Creo Control Active”控件,控件的SLSID为{F07443A6-02CF-4215-9413-55EE10D509CC}。控件设置完成后,通过设置控件的相关属性,实现三维模型的数据读取、移动、旋转、放大、缩小等操作。
2.2.2 计算环境配置
软件开发的计算机上需安装Matlab。软件通过Matlab引擎实现对Matlab的调用和操作。在软件开发过程中,需要配置项目环境,选择项目“属性”按钮,在C/C++常规选项的附加包含目录选项中添加Matlab安装路径下的include相关根路径,在链接器常规选项的附加库目录选项中添加Matlab安装路径下的lib和win相关根路径,在链接器输入选项的附加依赖项中添加libeng.lib、libmat.lib、libmex.lib、libmx.lib、mclmcrrt.lib和mclmcr.lib,至此完成计算环境配置。
2.2.3 报表环境配置
本软件提供分析数据保存和分析报告生成功能,因此需要实现软件与Excel和Word数据间的交互。Qt提供与Office的数据接口,在程序头文件中添加
2.3 软件主界面
装配精度可靠性评估软件界面主要包括标题栏、工具栏、状态栏、功能区和工作区等,状态栏提示用户界面当前位置及相关操作,主界面如图3所示。

图3 装配精度可靠性评估软件主界面
2.4 软件分析流程
装配精度可靠性评估软件主要功能模块包括:装配误差传递建模、可靠性分析、分析结果查看和分析报告生成。图4为装配精度可靠性评估流程。
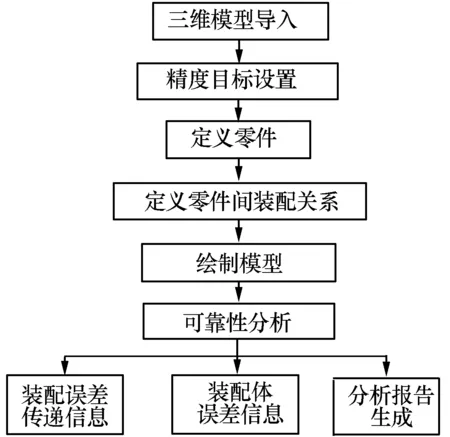
图4 装配精度可靠性评估流程
2.4.1 装配误差传递建模
装配误差传递建模是本软件的核心模块,主要包括模型导入、精度目标设置和误差传递模型构建3部分。模型导入用于导入分析对象的三维模型;精度目标设置用于设置精度上下限;误差传递模型构建主要包括定义零件、定义零件间装配关系、绘制模型3个步骤,完成定义零件(零件间装配关系)所需的零件关键点坐标(装配关键点坐标)、尺寸误差类型、尺寸误差上下限、角度误差类型、角度误差上下限等,完成分析对象物理模型和精度分析模型的构建。
2.4.2 装配精度可靠性计算
可靠性分析模块主要由可靠度计算部分组成,通过相关参数设置开展分析对象的装配精度可靠性分析,并得出可靠度及误差传递过程的相关结果。
2.4.3 分析结果查看
该模块包括误差传递信息和装配体误差信息2部分。“误差传递信息”可以查看装配体在装配过程各道工序中的尺寸、角度误差、误差分布及均方差变化情况;“装配体误差信息”可以查看装配体的相关尺寸、角度误差和误差分布情况。
2.4.4 分析报告生成
该模块用于生成机械产品装配精度可靠性分析详细报告,并提供阅览功能。分析报告内容包括:各零件详细信息、零件间装配信息、仿真基础参数信息、误差传递信息结果、装配体误差信息结果。
2.5 软件功能实现
2.5.1 误差传递模型构建功能
可靠性建模是软件的核心模块,其核心是误差传递模型的构建。软件界面左侧是误差传递模型构建区域,由定义零件、定义零件间装配关系和绘制模型3部分组成。界面右侧是分析对象的三维模型图,如图5所示。
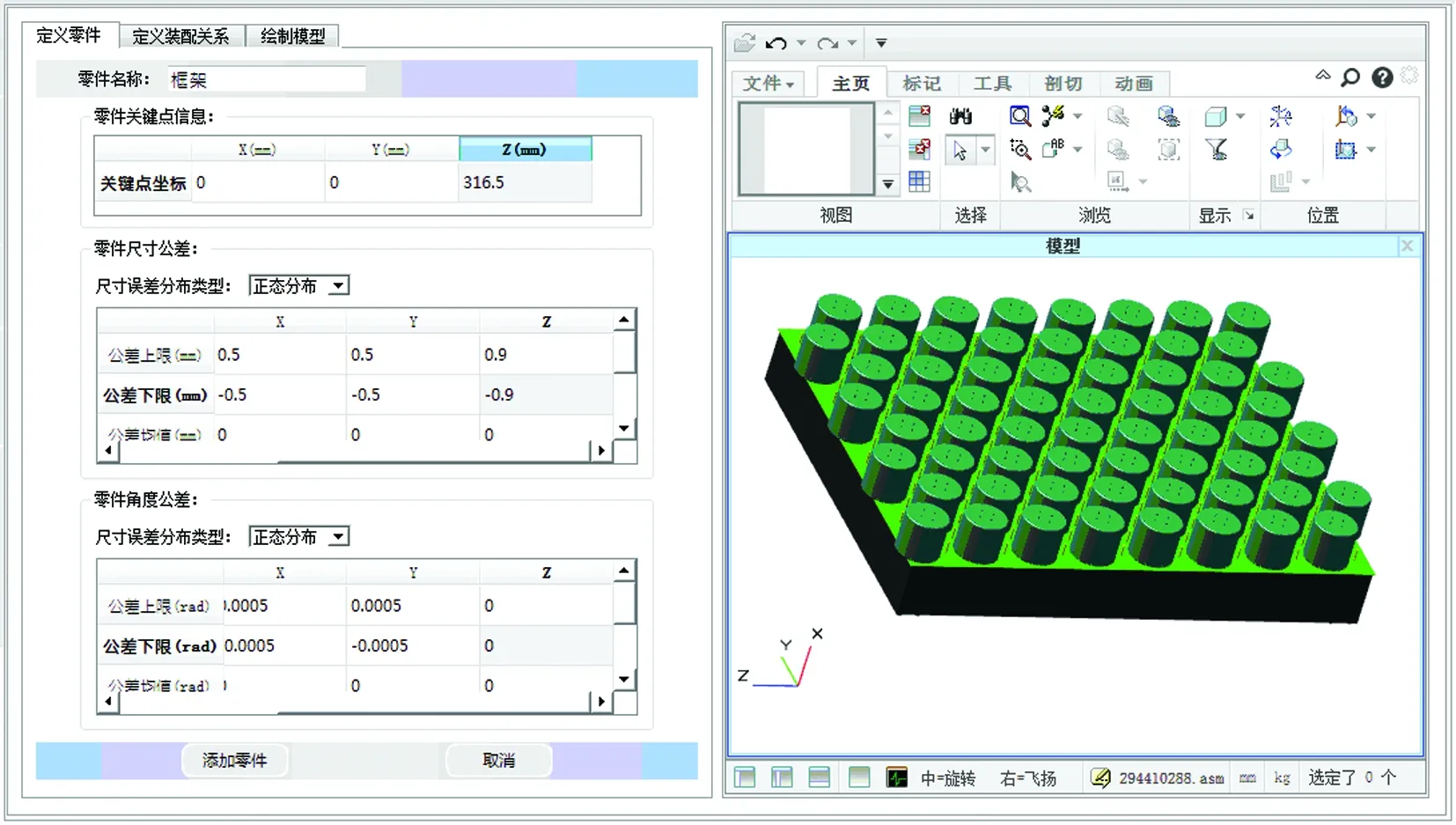
图5 零件定义界面
(1)定义零件
用户根据分析对象的零件组成(参考界面右侧的三维模型图)依次定义各零件。定义零件时需输入零件的关键点坐标(也可通过鼠标在三维模型中点击零件关键点自动输入),选择零件尺寸误差的分布类型(包括正态分布、瑞利分布和均匀分布),输入零件在x、y、z三个方向的尺寸误差上下限,选择零件角度误差的分布类型,输入零件在x、y、z三个方向的角度误差上下限(弧度制),信息输入完成后点击“添加零件”按钮,局部界面如图5所示。
(2)定义零件间装配关系
零件定义完成后,已定义的零件将自动加载到零件名称组合框。用户依次选择各零件为当前零件,未选中的零件将自动加载到可装配件列表框中,根据装配体的装配关系选择当前零件的前后装配件,关键点坐标、尺寸误差和角度误差的输入与定义零件时相似,信息输入完成后点击“确定”按钮,局部界面如图6所示。

图6 装配关系定义界面
(3)绘制模型
零件和零件间装配关系定义完成后,工作区左侧的绘制模型区将显示已经定义的零件,用户可用鼠标选中零件任意拖动,根据装配关系将零件放置在合适的位置,以便于查看零件间的装配关系。工作区右侧为装配体的三维模型图,局部界面如图7所示。

图7 模型绘制界面
2.5.2 可靠性分析功能
在三维模型导入、装配精度设置和误差传递模型构建完成后,装配精度可靠性评估模型构建完成,用户输入仿真次数,点击“可靠性计算”按钮即可得出装配精度可靠度,并显示在工作区右上侧。工作区左侧显示构建的误差传递模型,工作区右侧动态显示可靠性分析的计算进度,如图8所示。

图8 可靠性分析界面
2.5.3 分析结果查看功能
装配体装配精度可靠性建模和分析之后,即可查看可靠性分析结果。分析结果由误差传递信息和装配体误差信息2部分组成。
(1)误差传递信息
用户可通过组合框选择查看的误差方向和类型。工作区左上侧显示误差在各工序的均方差及均方差变化趋势,工作区左下侧显示相应方向、相应类型各工序误差的分布图形,工作区右侧显示相应方向、相应类型各工序每次仿真的误差值,如图9所示。
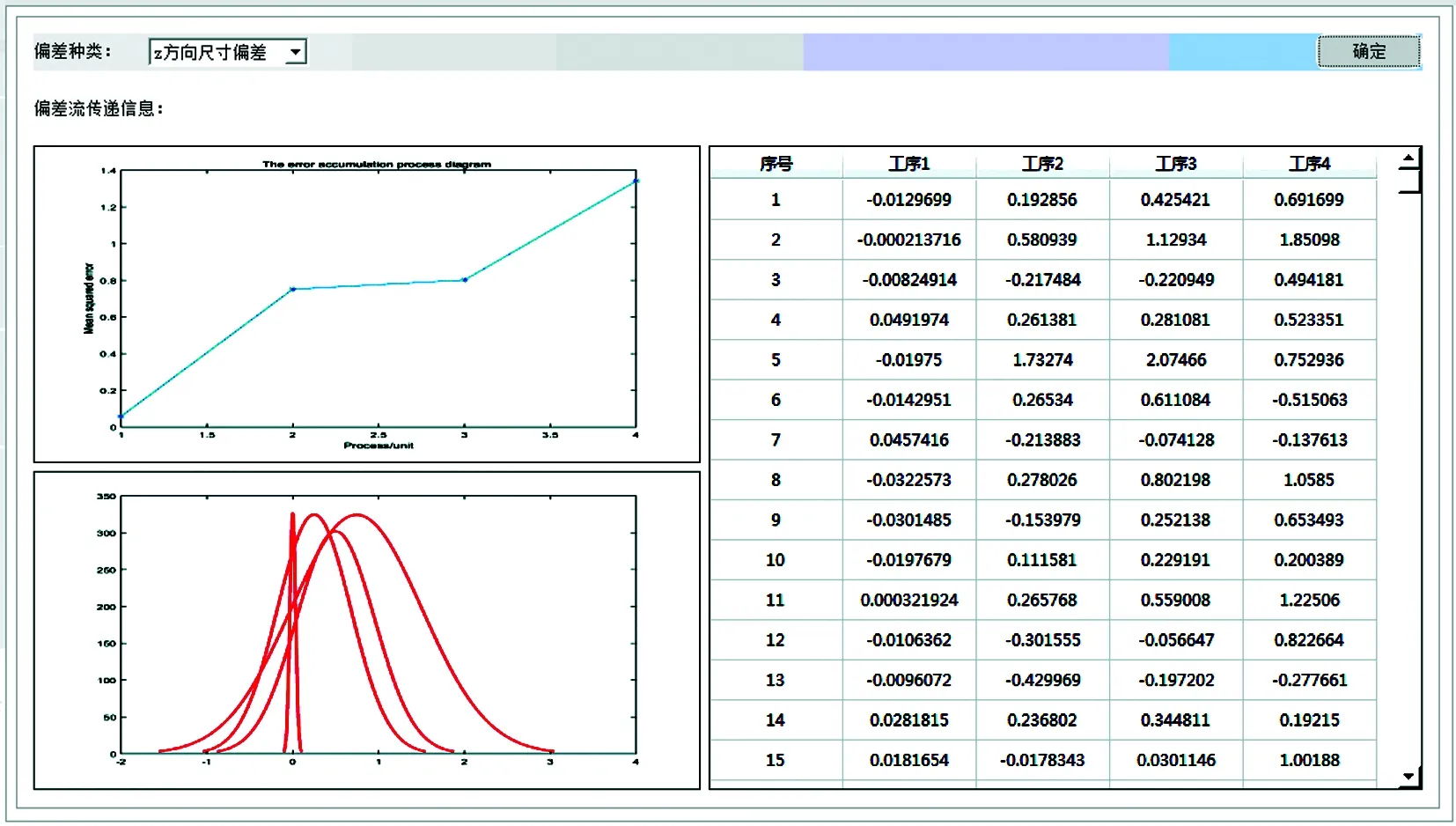
图9 误差传统信息界面
(2)装配体误差信息
用户可通过组合框选择查看的误差方向和类型,工作区左侧显示相应方向、相应类型的天线阵子模块误差分布图形,工作区右侧显示相应方向、相应类型天线阵子模块每次仿真的误差值,如图10所示。

图10 天线阵子模块误差信息界面
2.5.4 案例分析结果
本文以某型天线阵子模块为例,根据实际参数,验证天线阵子模块装配精度可靠性评估软件的功能。天线阵子模块由4个铰链、框架、反射板和64个天线阵子单元组成。通过导入三维模型,设置天线阵子模块精度上下限,输入各零件及装配的关键点信息、尺寸误差和角度误差信息,建立天线阵子模块装配精度可靠性分析模型并开展可靠性分析,得出该天线阵子模块装配精度可靠度为0.832 4,并得出x、y、z三个方向误差在各工序的分布图以及装配过程中x、y、z三个方向误差在各工序之间的积累和传递情况。
天线阵子模块设计者根据本软件的分析结果,对各零件和装配处的误差开展优化和再分配,提高了天线阵子模块的装配精度可靠性,取得了良好的应用效果。
3 结束语
本文在装配精度及其可靠性评估理论研究基础上,开发机械产品装配精度可靠性评估软件,有效地减少了装配精度可靠性评估的难度及工作量。所开发的软件具有一定的通用性,案例研究验证了软件功能的有效性。
后续研究内容包括机械产品装配精度分配以实现装配体精度改善,装配精度薄弱环节识别等功能模块。
[1] 杨叔子. 机械装配[M]. 北京: 机械工业出版社, 2012.
[2] HU S J, KOREN Y. Stream-of-variation theory for automotive body assembly[J]. CIRP Annals - Manufacturing Technology, 1997, 46(1): 1-6.
[3] JIN J H, SHI J J. State space modeling of sheet metal assembly for dimensional control[J]. Journal of Manufacturing Science and Engineering, 1999, 121(4): 756-762.
[4] CHEN J S. Computer-aided accuracy enhancement for multi-axis CNC machine tool[J]. International Journal of Machine Tools and Manufacture, 1995, 35(4): 593-605.
[5] ASANTE J N. A small displacement torsor model for tolerance analysis in a workpiece-fixture assembly[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2009, 223(8): 1005-1020.
[6] 毛英泰. 误差理论与精度分析[M]. 北京: 国防工业出版社, 1982.
[7] 余治民, 刘子建, 艾彦迪, 等. 大型数控龙门导轨磨床几何误差建模与基于可靠性理论的精度分配[J]. 机械工程学报, 2013, 49(17): 142-151.
[8] 张可欣, 万其, 李忱. 雷达系统中的印制板可靠性预计分析软件设计[J]. 电子机械工程, 1998(5): 43-46.
[9] 贺鹏. 机械可靠性及其在雷达结构设计中的应用[J]. 电子机械工程, 2010, 26(5): 7-9, 12.
