平面阵雷达振动变形特性分析
2017-03-08侯守武
侯守武
(1. 中国电子科技集团公司第三十八研究所, 安徽 合肥 230088; 2. 国家级工业设计中心, 安徽 合肥 230088)
引 言
平面阵天线定向性强,易于根据实际需求形成单波束、多波束、赋形波束和锥状波束,还可以通过扫描的方式使其主波瓣指向空间的任一方向,现已广泛应用于雷达跟踪、制导、地物测绘、气象探测和导航等军民雷达领域[1]。为保证平面阵天线的电性能指标,单元的安装精度具有较高的要求。在振动、重力、温度等环境载荷下,雷达阵面的变形误差引起天线单元的相对位置发生变化,影响天线的增益、旁瓣电平和指向精度[2]。因此,在设计过程中需要对雷达天线在振动载荷下的变形进行分析,严格控制天线变形量。文献[3]利用有限元法分析了某相控阵天线在重力和温度载荷下的变形,基于最佳吻合平面算法获得天线阵面的静态平面度误差和方位指向误差。文献[4]通过建立随机振动对机载雷达阵列天线电性能影响的数学模型,分析了随机振动对雷达天线电性能的影响,提出了一种考虑随机振动影响的机载雷达机电综合设计方法。
本文提出利用最小二乘法评定平面度来分析平面阵的变形误差,采用坐标变换方法获得变形平面的转动角度和平动位移,评估平面阵的变形特性。通过计算某平面阵雷达的振动变形,提取雷达阵面的变形位移,利用最小二乘法拟合变形后的平面,获得阵面的平面度,并进一步分析雷达阵面的整体转动角度和平动位移,全面评估雷达在振动环境下的变形特性。
1 最小二乘法评定平面度
最小二乘法评定平面度的方法是采用实际测量平面的最小二乘中心平面作为理想基准平面,平面度为实际平面相对理想平面的变动量[5]。
平面方程的表达式为:
z=ax+by+c
(1)
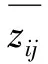
(2)
根据极限定理,有:
(3)
简化式(3)并写成矩阵形式:
AT=B
(4)
式中:
则:
T=A-1B
(5)
根据点到平面距离公式:
(6)
可以计算出所有测点到最小二乘中心平面的距离,中心平面一侧的点的距离为正值,另一侧为负值,实际平面的平面度为max(d)-min(d)。
2 空间坐标变换方法评定平面刚性位移
2.1 空间坐标变换
平面变形前后的坐标值均在全局坐标系中得到,变形后平面转动的评定基于变形前平面的坐标系,因此,评定平面转动角度时,首先将变形前后平面的全局坐标值变换到变形前平面的局部坐标系中。
设全局坐标系和局部坐标系分别为O-XYZ和O′-X′Y′Z′(见图1),点O′在全局坐标系中的坐标为(x0,y0,z0),设局部坐标系相对于X、Y、Z轴按右手定则旋转的角度分别为α、β、γ,则由O-XYZ变换到O′-X′Y′Z′的变换公式为:
P=RP′+T
(7)
式中:全局坐标P=[xyz]T,局部坐标P′=[x′y′z′]T,平动向量T=[x0y0z0]T,旋转矩阵:
式中:
r11=cosβcosγ
r12=-cosαsinγ+sinαsinβcosγ
r13=sinαsinγ+cosαsinβcosγ
r21=cosβsinγ
r22=cosαcosγ+sinαsinβsinγ
r23=-sinαcosγ+cosαsinβsinγ
r31=-sinβ
r32=sinαcosβ
r33=cosαcosβ
当转角α、β、γ均很小时,r11=1,r12=-γ,r13=β,r21=γ,r22=1,r23=-α,r31=-β,r32=α,r33=1,α、β、γ的单位为弧度。
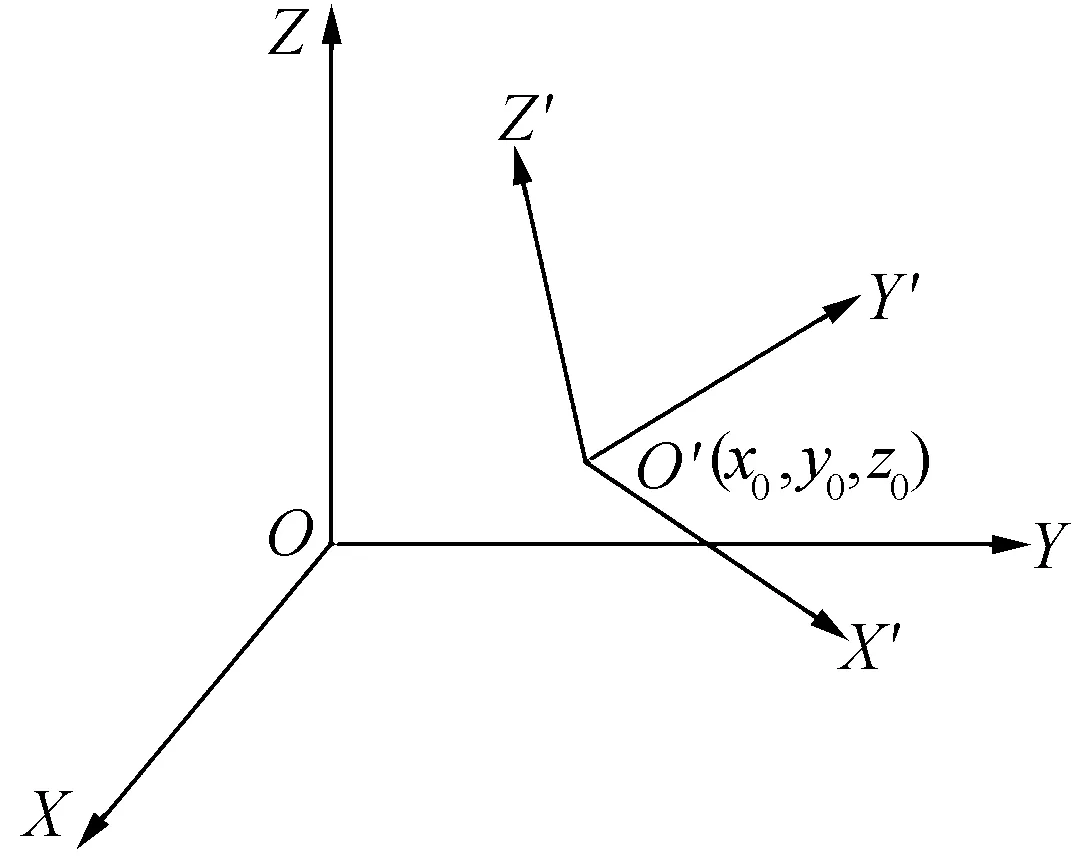
图1 空间坐标变换
2.2 变形平面的转动角度

(8)
(9)
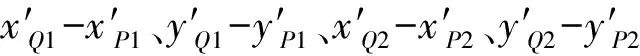
n1和n2与X′轴正方向的夹角:
(10)
(11)
则n1至n2的转角:
θZ′=θ2X′-θ1X′
(12)
同理可以求得绕X′轴和Y′轴的转角θX′和θY′。
2.3 变形平面的平动位移
变形后平面上各点均产生了相应的位移,每个测点的位移值也不尽相同,为考察平面的平动位移,以平面的形心在局部坐标系中的平动位移作为平面刚性变形量。
首先利用插值方法确定未变形平面形心PC的坐标(xC,yC,zC),或者将测点选定在平面形心,过形心且与最小二乘拟合平面垂直的直线方程为:
(13)
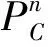
(14)
3 平面阵雷达振动变形特性分析
3.1 平面阵雷达分析模型
某平面阵雷达结构如图2所示,由机械结构和阵面构成,其中机械结构包括支架、旋转部件、框架。在有限元分析模型中,支架和阵面采用壳单元,框架和旋转部件采用实体单元,框架上的负载以集中质量模拟。定义模型坐标系原点位于旋转部件转轴中心,阵面法向为z轴方向,坐标系符合右手定则,坐标系方向如图中所示。
3.2 雷达结构振动变形
雷达结构振动试验条件:20~500 Hz恒加速度正弦振动,加速度幅值为2g。正弦振动时,当激励频率与固有频率吻合时,结构的振动变形最大。以振动试验载荷施加于支架安装位置,计算雷达结构的振动响应。
图3给出了激励载荷分别沿x、y、z向时,结构发生主方向一阶共振时的位移分布,最大位移分别为11.37 mm、1.797 mm和11.59 mm。最大变形均发生在远离支架一侧的阵面端部,其中x向激励时阵面绕z轴转动,y向激励时阵面绕x轴转动,z向激励时阵面绕x轴转动。
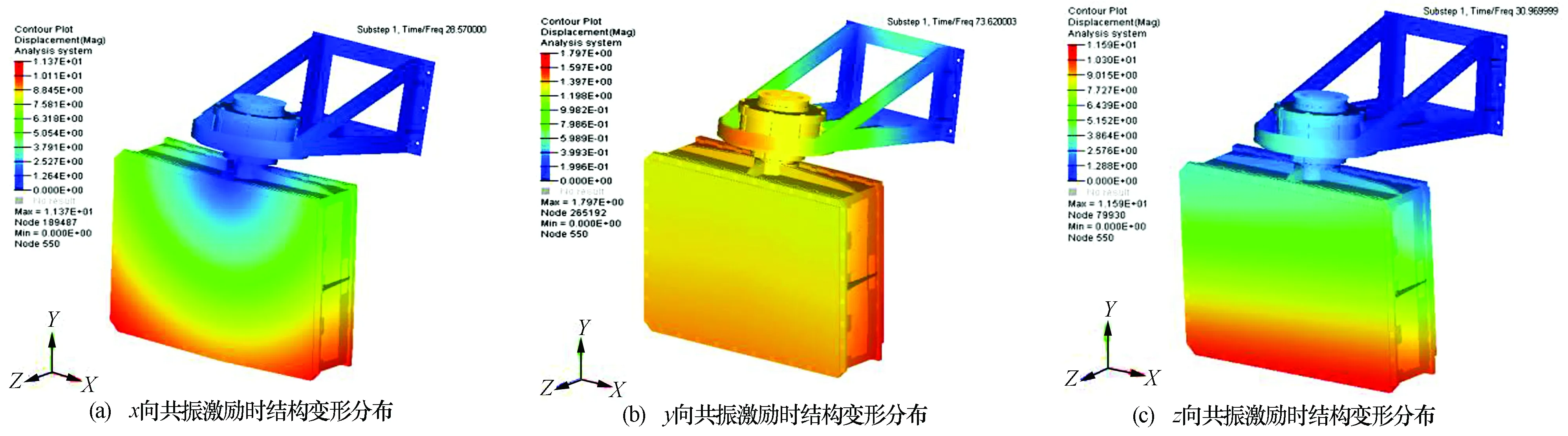
图3 结构共振时的变形分布
3.3 阵面变形特性分析
提取雷达阵面的振动位移,利用最小二乘法评定阵面平面度,利用空间坐标变换方法计算阵面的刚性位移。为全面反映雷达阵面的变形特性,在阵面表面选取均布的9行9列共81个节点。
图4给出了雷达阵面变形平面与拟合平面的空间位置,各阶模态共振时的平面度分别为0.25 mm、0.03 mm、0.16 mm,可见x向激励共振时平面度最大,为0.25 mm。从图中可以看出,x向激励时阵面发生了沿对角的翘曲,y向激励时阵面四角向下弯曲,z向激励时阵面沿短边向下弯曲。


图4 不同方向激励共振时阵面变形平面与拟合平面
x向激励共振时,阵面绕各坐标轴转动的角度分别为0.234 6°、0.066 4°、1.652°,形心平动位移分别为0.009 mm、0.003 3 mm、0.806 9 mm。y向激励共振时,阵面绕各坐标轴转动的角度分别为0.134 6°、0.002 1°、0.000 7°,形心平动位移分别为0 mm、0.001 mm、0.409 9 mm。z向激励共振时,阵面绕各坐标轴转动的角度分别为1.778 2°、-0.010 7°、0.222 4°,形心平动位移分别为0.000 5 mm、0.191 4 mm、6.169 1 mm。从雷达阵面变形前后的相对位移(图5)可以明显看出,x向激励共振时,阵面表现为绕z轴转动的同时绕x轴转动,y向和z向激励共振时,阵面表现为绕x轴转动的同时沿z轴上移。
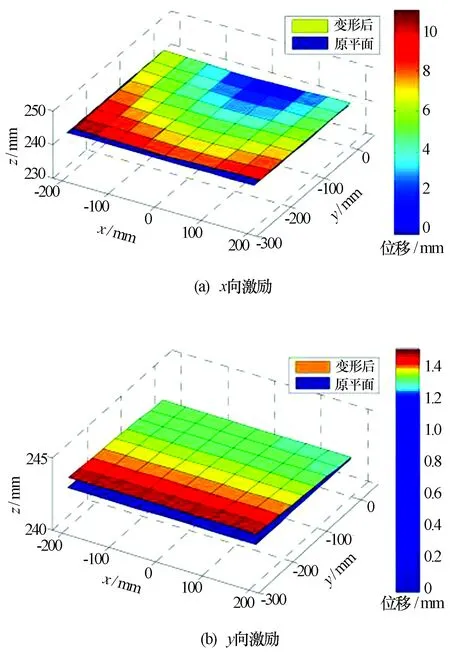
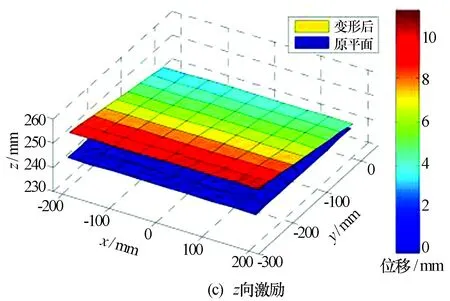
图5 不同方向激励共振时阵面变形平面与原始平面
4 结束语
本文利用最小二乘法拟合变形平面的理想平面,评定变形平面的变形误差,采用坐标变换方法计算变形平面的刚性位移,获得变形平面相对于原始平面的转动和平动量,评估平面阵雷达在振动环境下的变形。通过计算某平面阵雷达的平面度、刚性转动角度和平动位移,全面分析了平面阵雷达在振动环境下的振动变形特性。
[1] 高慧莲. 相控阵天线阵面热变形规律研究[D]. 西安: 西安电子科技大学, 2009.
[2] 矫志宁. 某机载雷达发射机的随机振动分析[J]. 电子机械工程, 2013, 29(2): 18-20, 23.
[3] 王昭. 某相控阵天线阵面静态仿真分析[J]. 电子机械工程, 2012, 28(6): 23-26.
[4] 郭睿. 机载雷达阵列天线随机振动分析与机电综合设计[D]. 西安: 西安电子科技大学, 2014.
[5] 周景亮, 林志熙. 大型平面平面度误差的可视化数据处理[J]. 机床与液压, 2009, 37(10): 130-132, 136.
