基于稀疏先验和相对总变分的图像盲去模糊*

姚若河 饶敬松 刘伟俭

(1.华南理工大学 电子与信息学院, 广东 广州 510640; 2.广东威创视讯科技股份有限公司， 广东 广州 510670)

图像运动模糊是现实中常见的问题，在过去的几十年里受到了广泛的关注.模糊过程的数学模型可描述为:模糊图像是清晰图像与模糊核卷积再加上噪声的结果[1- 2].噪声是零均值高斯噪声.其中模糊图像是已知量，模糊核和清晰图像是未知量.图像去模糊就是从模糊图像复原出清晰图像.根据模糊核是否已知,图像去模糊问题分为盲去模糊和非盲去模糊[3].在图像盲去模糊中,从单一模糊图像估计模糊核是个严重不适定问题.早期的图像盲去模糊主要是估计小尺度的模糊核,Chan等[4]采用总变分正则化方法估计模糊核,You等[5]提出一种变分架构估计小尺度高斯模糊核.但当模糊核呈现出复杂结构和图像有噪声时,上述方法估计出的模糊核不准确，且复原出的图像出现严重的振铃现象.

近年来,图像盲去模糊由于涉及正则化和优化问题而在数字图像领域被广泛研究.Fergus等[6]提出用零均值混合高斯模型拟合自然图像梯度的重尾分布,并采用变分贝叶斯算法进行图像盲去模糊;Levin等[7- 8]给出了最大后验概率方法的限制,并提出一种有效的边缘概率近似的方法,但估计出的模糊核含有噪声,不能很好地恢复图像细节;Krishnan等[9- 10]引入L1/L2稀疏图像正则项用于模糊核估计,并采用快速超拉普拉斯方法估计清晰图像.

另一类图像盲去模糊方法是基于显著边缘预测估计模糊核[11- 16].显著边缘通常用冲击滤波器对模糊图像的边缘进行增强[11],然后通过边缘选择算子得到.Cho等[12]用双边滤波和冲击滤波器得到锐利边缘,并采用高斯先验约束快速求解模糊核,但得到的模糊核常含有噪声且不是稀疏的，复原的图像出现振铃现象.Xu等[13]提出一种边缘选择准则得到不含小尺度物体(窄条)边缘的显著边缘,且在模糊核估计时采用迭代支持检测算法[14]去除模糊核的噪声.Pan等[15]在提取边缘前运用自适应TV预处理图像,减少噪声和小尺度物体边缘对模糊核估计的干扰.Xu等[16]运用广义L0稀疏先验得到阶跃边缘，并结合高斯先验约束估计模糊核.

文中提出用权值L0自适应地提取图像主体结构，剔除图像中的噪声、细节和小尺度物体边缘等不利于模糊核估计的因素.针对稀疏先验作为正则项估计模糊核的不准确性问题[9，12，17],提出相对总变分对模糊核进一步修正,改善模糊核的稀疏性和连续性.

1 显著边缘提取

基于显著边缘估计模糊核的图像盲去模糊方法的边缘提取至关重要,图像的噪声和细节会严重破坏模糊核的估计.为了排除噪声和细节的干扰,文中采用权值L0范数对图像进行预处理,剔除噪声和小尺度细节,得到主体结构.权值L0梯度平滑优化模型为

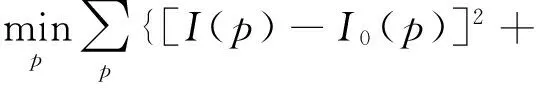
(1)

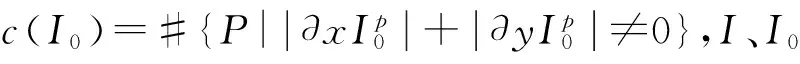
(2)

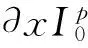
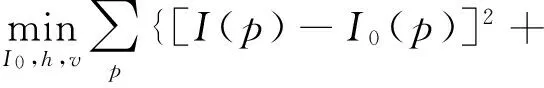
(3)

其中c(h,v)=#{p||hp|+|vp|≠0},参数β控制辅助变量和对应梯度的相似度.通过交替能量最小化求解模型(3).

(1)求解I0.由式(3)去除不含I0的项得到:

(4)

通过快速傅里叶变换进行加速求解：

I0=

(5)

式中，F表示傅里叶变换,F(·)*表示傅里叶变换复数共轭.

(2)求解h、v.由式(3)去除不含h、v的项得到：

(6)

因为c(h,v)在梯度不为0时为1,在梯度为0时为0,所以可以证明得到

(7)

权值L0得到的主体结构和文献[15]得到的主体结构如图1所示.由图1可见，用权值L0得到的主体结构能更好地去除细节和小尺度物体边缘,有利于模糊核的估计.

图1 图像主体结构结果Fig.1 Results of image main structure

得到主体结构I0后,阶梯型边缘有利于模糊核估计,进一步用冲击滤波器增强边缘,产生阶梯型边缘:

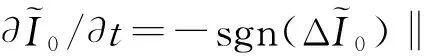
(8)

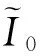
(9)

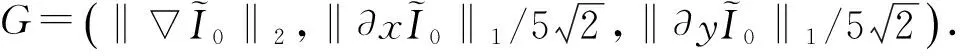
(10)

其中，Gi为G中一个梯度算子.

2 模糊核估计

从单幅模糊图像中估计出模糊核是个严重的不适定问题,为了使问题适定,需要引入模糊核的先验知识进行约束求解.图像的形成是光子(能量)的累积过程,所以模糊核满足非负性,更为重要的是模糊核通常满足稀疏性.运动模糊图像是由运动造成的模糊,而运动是连续的,所以模糊核也应该满足连续性.为了保证模糊核的稀疏性和连续性,用L1/2超拉普拉斯先验和相对总变分共同求解模糊核:

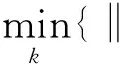
(11)

s.t.k(x)≥0;∑k(x)=1.

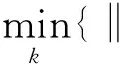
(12)

s.t.k(x)≥0;∑k(x)=1.

(13)

其中:

(14)

k0表示修正后的模糊核;ε为常数,保证c1(k0)分母不为0;R(p)表示中心在p点的矩形窗口;gp,q是高斯函数,决定着p、q点的空间关联:

(15)

其中,σ控制着窗口的空间尺度.

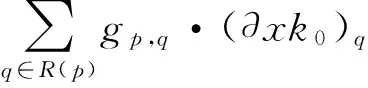
先用迭代重加权最小二乘方法[19]求解式(12),得到了一个含有噪声的模糊核,再用式(13)对模糊核进行平滑和修正,其中，式(13)可采用数值分析方法[20]求解.

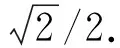
文中得到的模糊核与其他文献方法得到的模糊核进行对比,结果如图2所示.由图2可见：文献[9]采用稀疏先验正则项估计模糊核,得到的模糊核具有较多噪声；文献[16]虽然得到了结构较好的模糊核,但是模糊核中仍然含有孤立点；文中算法得到的模糊核更好地保持了连续性和稀疏性.

得到的模糊核 得到的模糊核 得到的模糊核

图2 模糊核估计结果
Fig.2 Results of kernel estimation

3 清晰图像复原

有效的非盲去模糊算法能够很好地解决由不准确模糊核估计带来的噪声和振铃现象.总变分正则化方法[21- 22]和稀疏先验正则化方法[23]经常被用于复原图像.总变分方法由于“阶梯效应”不能很好地保护复杂结构区域的细节和纹理，但研究发现超拉普拉斯先验更符合自然图像梯度分布规律，复原得到的清晰图像具有很好的主体结构和较少的振铃现象，所以采用超拉普拉斯先验来恢复清晰图像:

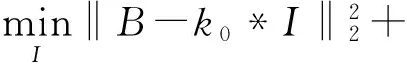
(16)

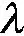
输入:模糊图像B和模糊核的大小.

将图像分成n层

fori=n:-1:1

设图像每一层图像为Bi;

forj=1:1:iter

通过式(1)得到主要结构I0;

通过求解式(12)、式(13)估计出模糊核k0;

估计清晰图像通过求解模型(16);

阈值t=0.9×t;

end

放大图像得到新的Ii用于下一级模糊核估计

end

输出:模糊核k0和清晰图像I.

4 实验结果

对3组图像进行实验.在提取显著结构中参数β初始值设为105,其每次迭代放大的比例取值为2,h取值为5.阈值t初始值设为1,在每次迭代后乘以0.9.在求解模糊核中,窗口尺度σ一般设为0～3之间.

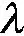
图3 图像去模糊结果(第1组)Fig.3 Results of image deblurring(First group)

图4 图像去模糊结果(第2组)Fig.4 Results of image deblurring(Second group)

图5 图像去模糊结果(第3组)Fig.5 Results of image deblurring(Third group)

5 结论

文中针对单幅运动模糊图像盲去模糊,提出权值L0自适应地提取图像的主体结构,剔除图像中的噪声、细节和小尺度物体边缘等不利于模糊核估计的因素.为了保证模糊核的稀疏性和连续性,采用超拉普拉斯先验和相对总变分估计模糊核,相对总变分能很好地克服稀疏先验作为正则项估计模糊核的不准确性.在图像非盲去卷积时,采用符合自然图像梯度分布的超拉普拉斯先验作为正则项复原出清晰图像,得到的图像具有更好的结构和更少的伪迹.

[1] LU Qing-Bo,ZHOU Wen-Gang,FANG Lu,et al.Robust blur kernel estimation for license plate images from fast moving vehicles [J].IEEE Transactions on Image Processing,2016,25(5):2311- 2323.

[2] CAI Jian-Feng,JI Hui,LIU Chao-Qiang，et al.Framelet based blind motion deblurring from a single image [J].IEEE Transactions on Image Processing,2012,21(2):562- 572.

[3] JIA J.Mathematical models and practical solvers for uniform motion deblurring(in Motion Deblurring:Algorithms and Systems) [Z].Hongkong:Cambridge University Press,2014.

[4] CHAN T,WONG C.Total variation blind deconvolution [J].IEEE Transactions on Image Processing,1998,7(3):370- 375.

[5] YOU Y L,KAVEH M .Blind image restoration by anisotropic regularization [J].IEEE Transactions on Image Processing,1999,8(3):396- 407.

[6] FERGUS R,SINGH B,HERTZMANN A,et al.Removing camera shake from a single photograph [J].ACM Trans-actions on Graphics,2006,25(3):787- 794.

[7] LEVIN A,WEISS Y,DURAND F,et al.Understanding and evaluating blind deconvolution algorithms [C]∥Proceedings of 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.Miami,FL:IEEE Computer Society,2009:1964- 1971.

[8] LEVIN A,WEISS Y,DURAND F,et al.Efficient marginal likelihood optimization in blind deconvolution [C]∥Proceedings of 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.Providence,RI:IEEE Computer Society,2011:2657- 2664.

[9] KRISHNAN D,TAY T,FERGUS R.Blind deconvolution using a normalizedsparsity measure [C]∥Proceedings of 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.Providence,RI:IEEE Computer Society,2011:233- 240.

[10] KRISHNAN D,FERGUS R.Fast image deconvolution using hyper-laplacian priors [C]∥Proceedings of Confe-rence and Workshop on Neural Information Processing Systems.Whistler,BC:NIPS,2009:1033- 1041.

[11] OSHER S,RUDIN L.Feature-oriented image enhancement using shock filters [J].SIAM Journal on Numerical Analysis,1990,27(4):919- 940.

[12] CHO S,LEE S.Fast motion deblurring [J].ACM Transactions on Graphics,2009,28(5):89- 97.

[13] XU L,JIA J.Two-phase kernel estimation for robust motion deblurring [C]∥Proceedings of European Confe-rence on Computer Vision.Heraklion,Crete:ECCV,2010:157- 170.

[14] WANG Y,YIN W.Compressed sensing via iterative support detection [J].SIAM Journal on Imaging Sciences,2009,4359(3):462- 491.

[15] PAN Jin-Shan,LIU Ri-Sheng,SU Zhi-Xun,et al.Kernel estimation from salient structure for robust motion deblurring [J].Signal Processing Image Communication,2013,28(9) :1156- 1170.

[16] XU L,ZHENG S,JIA J.Unnatural l0 sparse representation for natural imagedeblurring [C]∥Proceedings of 2013 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops.Portland,OR:IEEE Computer Society,2013:1107- 1114.

[17] SHAN Q,JIA J,AGARWALA A.High-quality motion deblurring fromasingle image [J].ACM Transactions on Graphics,2008,27(3):15- 19.

[18] XU L,LU C,XU Y,et al.Image Smoothing via L0 gra-dient Minimization [J].ACM Transaction on Graphics,2011,30(6):61- 64.

[19] DAUBECHIES I,DEVORE R,FORNASIER M,et al.Iteratively re-weighted least squares minimization for sparse recovery [J].Communication on Pure & Applied Mathematics,2010,63(1):1- 38.

[20] XU L,YAN Q,XIA Y,et al.Structure extraction from texture via relative total variation [J].ACM Transaction on Graphics,2012,31(6):439- 445.

[21] HE Chuan,HU Chang-Hua,ZHANG Wei,et al.Fast total-variation image deconvolution with adaptive parameter estimation via split bregman method [J].Mathematical Problems in Engineering,2014,2014(1/2/3/4):1- 9.

[22] WANG Y,YANG J,YIN W,et al.A new alternating minimization algorithm for total variation image reconstruction [J].SIAM Journal on Imaging Sciences,2008,1(3):248- 272.

[23] YANG J,ZHANG Y,YIN W.An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise [J].SIAM Journal on Scientific Computing,2009,31(4);2842- 2865.

[24] LEVIN A,FERGUS R,DURAND F,et al.Image and depth from a conventionalcamera with a coded aperture [J].ACM Transactions on Graphics,2007,26(3):70.