雷击特高压直流线路行波保护误动分析与优化策略*

蔡泽祥 田得良 梁益 李晓华 李书勇

(1．华南理工大学 电力学院， 广东 广州 510640； 2．中国南方电网电力调度控制中心， 广东 广州 510623； 3.中国南方电网科学研究院有限责任公司， 广东 广州 510080)

±800 kV特高压直流输电线路是目前世界上电压等级最高的直流输电线路,在跨区域电网间互联与大容量远距离输电中获得了广泛应用[1- 4].基于暂态电气量变化的行波保护是直流输电线路的主保护，其算法简单且动作迅速，行波保护的正确动作对保障特高压直流系统的稳定运行有重要意义.

特高压直流线路遭受雷击在实际运行中屡见不鲜[5]，加之特高压直流线路的两极间电位差很大，电磁耦合强度高，电网运行中已出现多起由雷击导致的行波保护误动事故.运行分析表明，发生频率最高的情况为较小幅值的雷电流绕过避雷线直接击中直流线路的一极，引起对极非雷击线路行波的保护误动，进而导致特高压直流系统双极相继闭锁的事故[6].因此，有必要开展雷击情况下非雷击线路的误动机理的分析、梳理，以提高特高压直流系统的运行可靠性.

目前，国内外学者已经对雷击情况下行波保护的响应特性以及误动机理展开了研究.文献[7]在实时数字仿真仪(RTDS)上用线路接入电压源的方式模拟了南方电网楚穗直流“6·5”行波保护误动事件，并提出了提高行波保护特征量门槛值的改进方法；文献[8]分析了行波保护的影响因素，提出了采用方向行波的新原理；文献[9]对不同故障情况下行波保护的整定方法进行了分析和改进.但是，以上研究仍限于针对具体事故的定性分析与反措，而且反措策略又往往带来保护动作的其他问题.例如，提高行波保护判据的门槛值会使线路在发生高阻、远距离接地故障时保护的灵敏性不足，从而造成保护拒动概率的增加.

文中以某实际特高压直流工程为背景，在EMTDC中搭建雷击模型并结合现场录波对模型的正确性进行了验证.在此基础上分析了行波保护误动时3个保护特征量的动态响应特性，并结合特征量在时序上的逻辑配合关系，指出在雷击故障发生后直流系统非雷击极恢复的过程中，导致行波保护误动发生的原因.基于以上分析提出了行波保护电压判据的闭锁逻辑，优化了行波保护判据间的时序配合.

1 雷击特高压直流线路暂态过程仿真

1.1 雷电流模型的建立

大量观测结果表明[10],自然界的雷电流随时间以近似指数关系上升至峰值,然后又以近似指数关系下降,如图1所示.

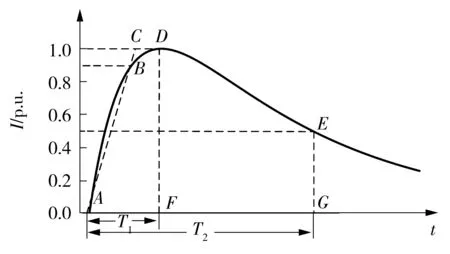
图1 雷电波波形Fig.1 Thunder current represented

图1中，T1和T2分别表示波头和波尾参数，在EMTDC雷电仿真模型中，通过双指数函数精确控制雷电流的波头时间和波尾时间[11]，得到雷电流解析式：

I=I0(e-αt-e-βt)

(1)

式中：t为雷电流进程时间；α和β分别是决定雷电流电流上升和衰减的时间常数，α=-1/T2，β=-1/T1；I0为受控电流源的电流，可以借此控制雷电流幅值.

1.2 研究系统概述

文中基于EMTDC[12]搭建了某特高压直流输电一次系统及其完整的控制保护系统，研究系统的参数如表1所示.

表1 研究系统基本参数Table 1 Basic parameters of primary system

1.3 特高压直流线路雷击暂态分析

在前文建立的雷电流模型基础上，以实际运行的某特高压直流工程在发生雷击线路一极，非雷击线路行波保护发生误动时的线路电气量现场录波为切入点，寻求雷击过程和线路暂态电气量变化过程之间的联系，进而为研究行波保护误动的机理提供依据.

雷电流在击中线路后形成幅值很高的冲击电压波[13]，同时交变的暂态电流在周围的空间形成交变的磁场，从而在非雷击线路上也感应出冲击电压波.因此，从线路遭受雷击后的暂态电压过程可以更精确地反映雷击线路的暂态响应特征.图2所示为某特高压直流线路一极遭受雷击时，行波保护安装处对直流线路电压UdH的现场录波图.

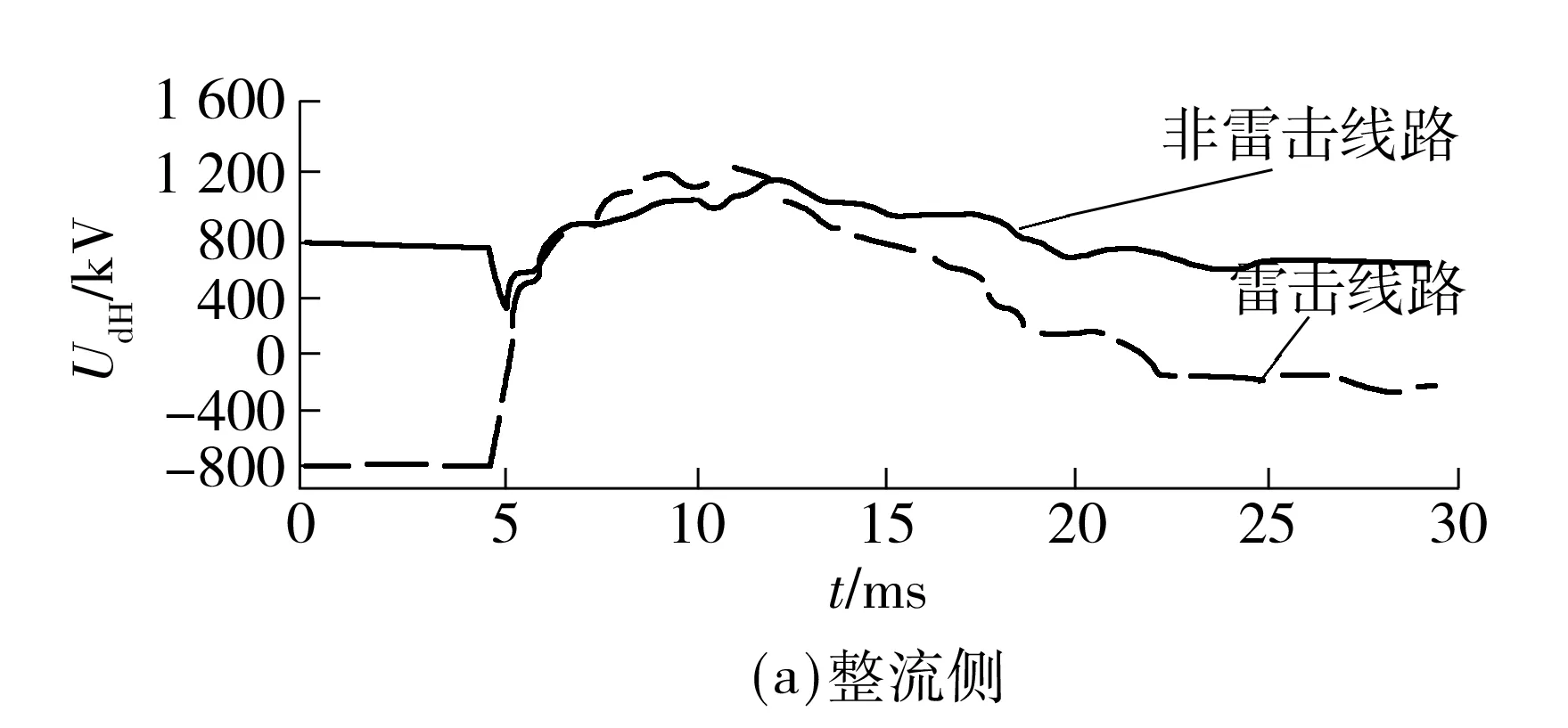
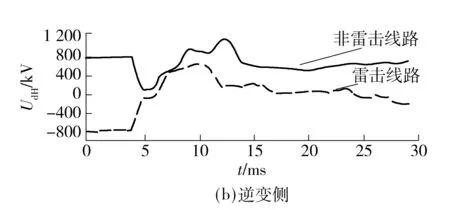
图2 雷击后保护安装处电压暂态过程录波

Fig.2 Voltage transient process of relay location after thunderstruck

从线路的电压暂态过程可以看出在负极线路遭受雷击后，雷击线路整流侧、逆变侧电压迅速反冲至正的+1 200 kV和+800 kV附近，表明负极线路遭受到了正极性的雷电流.在雷击发生后的大约5 ms后，正极和负极的电压再次明显升高至最大幅值，在此之后负极线路电压下降至0附近，正极线路电压逐渐恢复到正常状态.这表明线路遭受雷击后，在冲击电压波快速上升的过程中，当线路电压大于绝缘子闪络电压时，绝缘子被击穿，随后发展成线路接地故障，负极线路电压行波被截断，由此导致负极电压迅速衰减至0，正极线路电压则逐渐恢复.

在前文建立的EMTDC特高压直流线路雷击模型基础上，通过逐步增大雷电流、改变雷击点位置等方法重现上述线路电压暂态变化的特征.仿真结果表明，在雷电流增大到32 kA以上时出现了和实际现场录波相似的电气量变化特征，非雷击线路的行波保护发生了误动，同时观测到雷击线路绝缘子发生闪络，此时保护安装处直流线路电压UdH的仿真结果如图3所示.

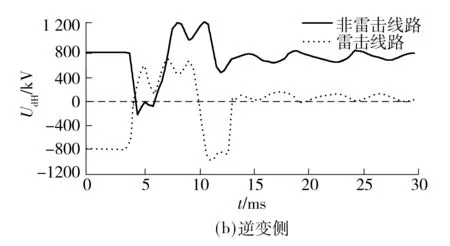
图3 雷击后保护安装处电压暂态过程仿真结果

Fig.3 Simulation results of voltage transient process of relay location after thunderstruck

与此同时，将图3和图2对比可以看出，在EMTDC中仿真的线路电压暂态过程和故障现场的录波变化趋势相吻合，从而验证了上述雷击建模和所选参数的正确性.

2 行波保护原理与雷击误动分析

在确定雷击模型的基础上，研究雷击一极而非雷击线路行波保护发生误动这一情况，分析当非雷击线路行波保护发生误动时保护特征量电压变化率dU/dt、电压变化量ΔU、电流变化量ΔI的动态响应特性，并结合3个特征量的时序逻辑关系，从特征量之间的时序配合的角度揭示行波保护发生误动的机理.

2.1 行波保护原理

典型特高压直流输电线路行波保护是取线路末端的电压、电流经过计算得到3个保护特征量，分别是dU/dt、ΔU以及ΔI.dU/dt的基本计算方法是对线路电压进行微分，结果表征线路电压波动速率，ΔU和ΔI的基本计算方法都是用当前时刻的电压、电流减去一段时间之前的电压、电流，结果表征线路电压、电流波动的剧烈程度[14].每一个特征量都有与之对应的门槛值，当故障行波沿线路传播至保护安装处时，如果特征量达到既定门槛值则认为满足了幅值条件[15- 16].但是，为了避免行波保护3个特征量偶然满足导致的保护误动，特高压直流线路行波保护引入特征量在时序上的配合，只有当3个特征量在满足了幅值条件的基础上又满足保护特定的时序关系时，行波保护才得以最终出口[17].

图4给出了某特高压直流线路行波保护3个特征量在时序上的简要逻辑关系图.其中，电压判据和电流判据同时对故障做出响应，如果以电压判据满足的时刻t0为参考，只要保证电压判据满足后展宽的12 ms和电流判据满足后展宽的6 ms在时间上有重叠，即电流判据满足时刻在tA和tB之间，行波保护便最终出口，如图5所示.对于电压判据，首先由特征量dU/dt达到幅值条件，在6 ms内只要特征量ΔU也满足其幅值条件，电压判据就得到满足；对于电流判据，整流侧的幅值条件是大于其门槛值，逆变侧则相反 .

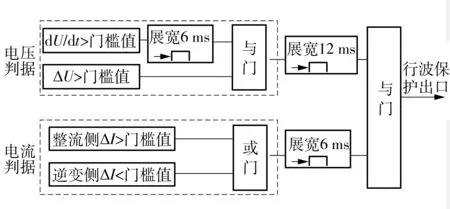
图4 某特高压线路行波保护特征量逻辑关系Fig.4 Logical relationship of characteristics of WFPDL

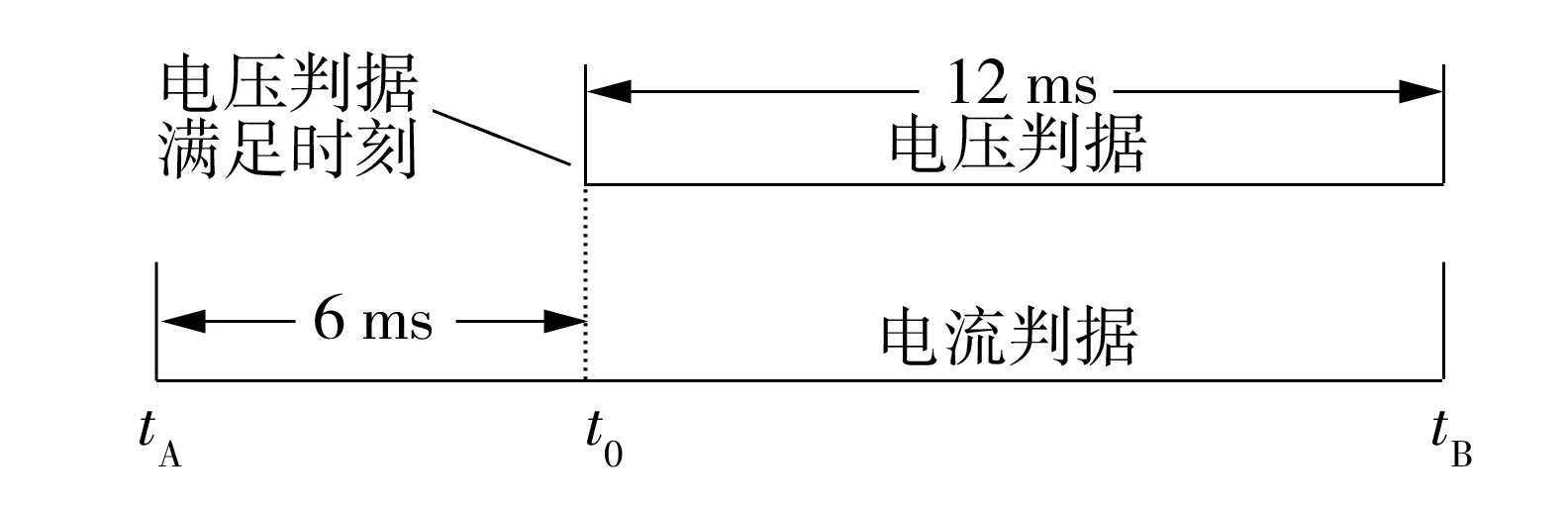
图5 行波保护电压判据和电流判据时序配合情况

Fig.5 Sequential coordination between voltage and current of WFPDL

2.2 行波保护误动分析

以上述的EMTDC仿真实例为背景，研究线路遭遇雷击导致行波保护误动情况下3个保护特征量dU/dt、ΔU、ΔI的动态响应特性以及在时序上的配合情况.以非雷击线路整流侧为例，图6给出了非雷击线路行波保护误动时3个特征量的暂态响应特性及其出口情况，同时分别表示了行波保护电压判据和电流判据的满足情况及行波保护最终出口动作情况.

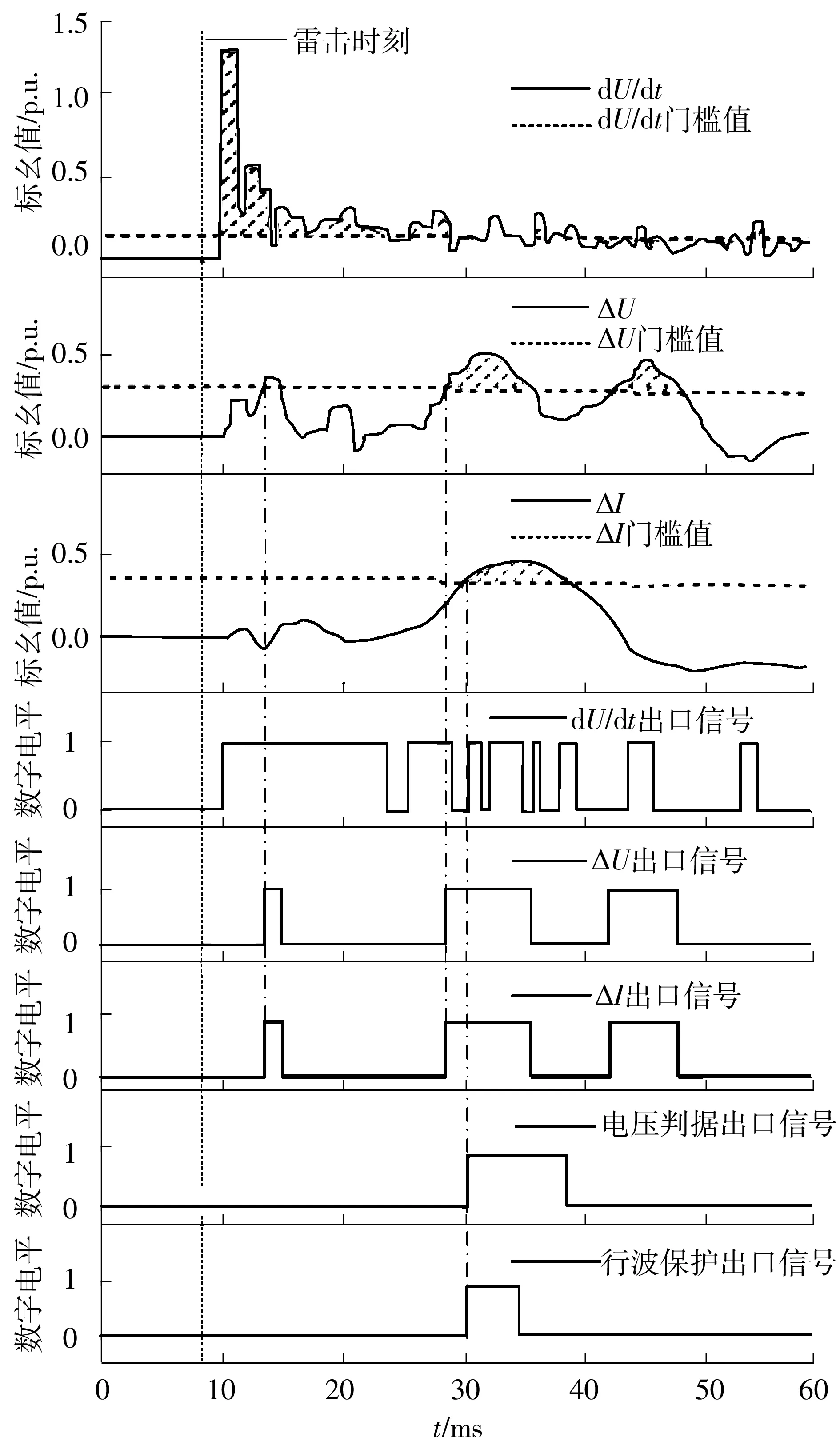
图6 非雷击线路整流侧行波保护误动时的响应情况

Fig.6 Response of WFPDL maloperation on non-lightening line in rectifier

结合1.3节中雷击暂态过程可以得出，在线路一极发生雷击事件后，由于强烈电磁耦合作用，非雷击线路电压也发生剧烈波动，特征量dU/dt迅速达到门槛值，考虑到其满足后展宽的时间，特征量dU/dt大约有15 ms的时间满足了幅值条件.在雷击事件发生大约5 ms后由于电压突变量达到峰值，特征量ΔU满足幅值条件，此时行波保护电压判据得到满足.但是由于线路遭受雷击后，绝缘子发生闪络使得线路通过杆塔接地，雷击线路中大量的能量通过杆塔向大地释放，直流线路两极间的电磁耦合强度也因此下降，非雷击线路电流变化量ΔI未满足门槛值，行波保护不满足出口条件.

雷击过程结束后，非雷击极在直流系统控制环节的作用下重新建立，由于线路电压的波动，特征量dU/dt仍会不断满足门槛值，加之其自身有6 ms的出口展宽时间，可以认为特征量dU/dt在雷击后较长时间内会一直满足幅值条件，即电压判据的满足情况只由特征量ΔU决定，如图6电流判据的出口情况所示.因此，在雷击后的19 ms左右时电压迅速回升使得特征量ΔU满足门槛值，行波保护电压判据随之满足，并延长高电平时间12 ms.在雷击后的21 ms左右时线路电流的持续上升使电流判据也得到满足，如图6电压判据的出口情况所示.此时，行波保护动作的时序条件满足，保护出口.逆变侧的特征量动态响应特性和整流侧相似，在此不再赘述.

由以上分析可以看出，在非雷击极受扰后的恢复阶段，随着线路输送功率的恢复，两极线路间的电磁耦合作用得以加强，使得非雷击线路电压、电流仍继续波动，因此会出现特征量ΔU和ΔI在雷击较长一段时间后仍能满足门槛值的情况.可见，雷击情况下非雷击线路行波保护误动的机理是直流线路一极遭受雷击后，非雷击极在恢复过程中，线路两极间强烈的电磁耦合致使非雷击线路电气量剧烈波动，引起保护特征量的响应特性改变使得恰好满足其既定的时序关系.

3 雷击情况下行波保护优化策略

3.1 电压判据优化策略的提出及分析

根据前文对某特高压直流线路行波保护误动的分析，并结合此工程实际运行中所发生的行波保护误动事件，可以看出行波保护误动发生的时刻都是发生在雷击事件后较长时间，如表2所示，此时直流系统非雷击极正处于受扰后的恢复阶段.由仿真分析(见图6)可知非雷击线路在雷击事件发生6、19、34 ms后电压判据都得到满足，考虑到行波保护的速动性，电压判据只有在第一次满足时才可能正确反应故障特征.因此，保证电压判据的正确满足就成为行波保护优化的一个思路.

表2 不同事故背景下非雷击线路行波保护误动情况

Table 2 Lightning line traveling wave protection misoperation under different accident background

事故背景误动状况误动位置事故结果实际事故1实际事故2EMTDC仿真算例雷击25ms后误动雷击15.5ms后误动雷击21ms后误动整流侧逆变侧整流侧逆变侧整流侧逆变侧双极闭锁双极闭锁双极闭锁

如前所述，特征量ΔU在受到雷击线路扰动后多次满足门槛值直接导致了电压判据的重复满足，因此，提高ΔU的门槛值成为最简单的方法.但是，提高门槛值必定会影响区内故障情况下保护的灵敏性，不能作为优化行波保护的最佳措施.下面讨论通过引入电压判据闭锁逻辑，使电压判据可以正确区分故障和扰动的工况，在不牺牲行波保护灵敏性的前提下提升保护选择性.

在现有行波保护电压判据中，特征量dU/dt和ΔU之间的配合逻辑处于开环状态，从而导致电压判据动作特性仅仅取决于特征量的动态响应.因此，可通过延长电压判据动作特性的下降沿延时，实现电压判据在第一次满足后Td时间内的闭锁，有效防止非雷击线路行波保护电压判据受到雷击线路的扰动后多次满足条件，优化后的电压判据逻辑如图7所示.

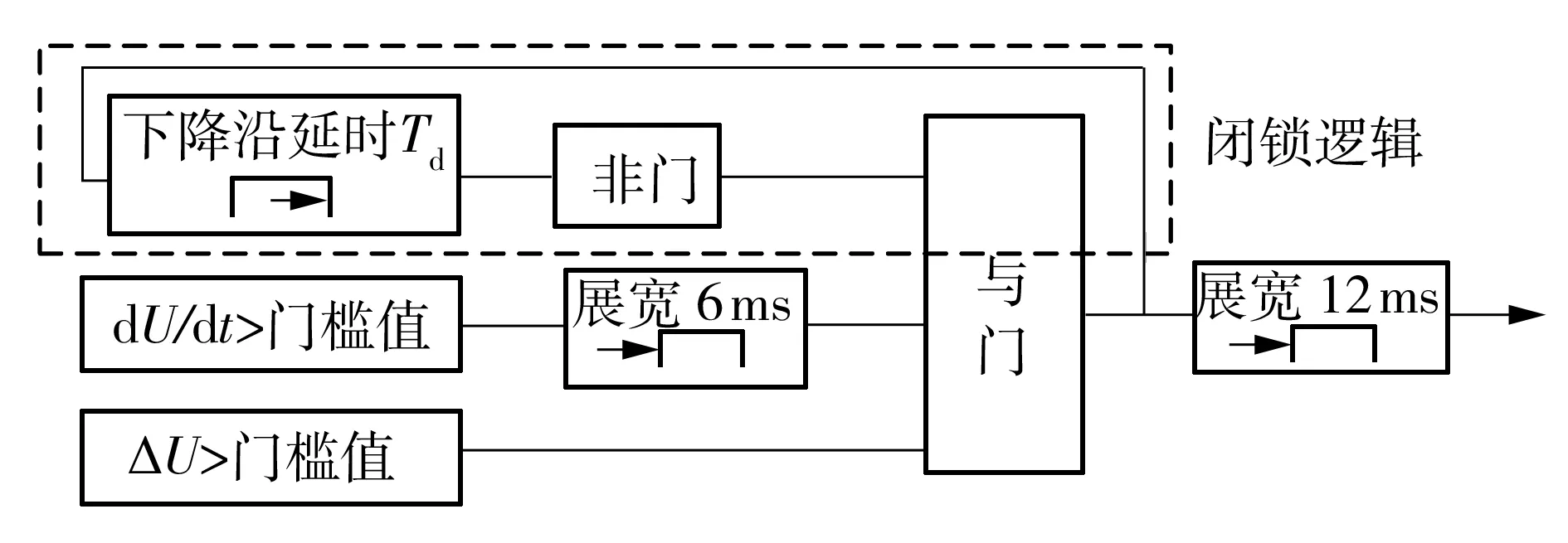
图7 优化后的行波保护电压判据Fig.7 Voltage criteria of WFPDL by optimization

3.2 电压判据闭锁逻辑Td的整定优化策略的提出及分析

在电压判据闭锁时间Td内行波保护要求能够充分反映故障特征，同时，应躲过由直流系统控制响应引起的特征量剧烈波动的时间，并留有相应的裕度，因此，需要根据行波保护的响应时间和直流控制环节的作用时间进行闭锁时间Td的整定.

首先，行波保护本身不带延时，行波保护的动作所需要的时间仅仅是由故障行波传递至保护安装处的时间TL和行波保护判据之间时序配合所需要的时间TP之和.因此，得到电压判据闭锁时间Td的一个边界为

Td1=TL+TP

(2)

其中，当直流线路中点发生故障时，故障行波沿线路传递至整流侧或者逆变侧所需要的最短时间最大.在本特高压直流工程中，线路长度的一半取707 km，故障行波传递速度取光速，故TL取值为2.4 ms.同时，根据2.1节所述，行波保护各判据在时序配合上所需的最长时间TP为18 ms.因此，在最不利的情况下确定Td1边界为20.4 ms.

下面，根据躲过控制环节响应的时间再次求取Td的边界值.在直流线路受扰动后，通过增大触发角α0使整流站直流电压UdH1迅速下降，控制系统起动低压限流环节(VDCOL)，直流电流迅速减小，等大扰动结束后，再逐步减小触发角α0，使直流系统恢复到故障前的直流电压和电流.整流侧电压和线路电流变化关系如式(3)、(4)所示：

(3)

(4)

式中：Ud0为整流侧换流母线电压；Xr1为整流侧换相电抗；R为直流线路电阻；UdH2为逆变侧直流线路电压.

低压限流环节的基本控制策略如图8所示，Iref、Uref分别为直流系统的参考电流和电压，与经过的实际电流和电压Ireal、Ureal在一段时间内求平均后的结果作差后取其较小值，经过比例积分环节求得触发角α0，再经过惯性环节作用于换流阀.控制环节响应的时间主要体现在电压、电流求平均的时间TA和触发角α0作用到换流阀的惯性环节滞后时间TG上.电压判据闭锁应躲过低压限流环节调整触发角α0先减小再增大的时间，因此，电压判据闭锁时间Td的另一边界为

Td2=TL+2(TA+TG)

(5)

其中，TA为5 ms，惯性环节的时间常数为0.5 s，结合仿真分析取TG为8 ms，TL取值仍为2.4 ms.因此，确定Td2的边界为28.4 ms.

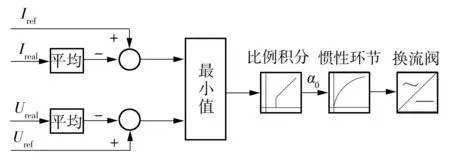
图8 低压限流环节的基本控制策略Fig.8 Basic control strategy of VDCOL

基于以上分析，取以上两个边界Td1和Td2的较大值并考虑相应裕度，最终取Td=35 ms进行下文优化策略的有效性验证.

3.3 电压判据优化策略的有效性验证

经过上述优化后的行波保护必须同时确保在非雷击情况下的不误动以及故障雷击情况下的不拒动.下面将分析优化后的行波保护是否会带来灵敏性以及新的选择性问题.

3.3.1 雷击故障情况

大量工程数据表明[18]，随着特高压直流线路电压等级提高，相应的绝缘水平增强，90%以上的雷击故障是由雷电直接绕击造成的.避雷线对较大幅值雷电流具有良好的屏蔽作用，因此只有极少一部分雷电流能够绕击直流线路，且雷电流幅值都较小，一般为40 kA以下，一次放电即可完成全部能量向线路的释放[19- 20].实际运行表明，在数十毫秒的短时间内发生两次及以上小幅值雷电流绕击线路的概率很小.因此，可以认为没有因为Td时间内电压判据的闭锁引入带来雷击情况下新的行波保护选择性问题.

在前文所述的雷击情形下，将优化后的行波保护进行仿真验证，雷击极线路行波保护正常动作，3个保护特征量间的配合符合行波保护快速动作的要求，如图9所示.非雷击线路行波保护电压判据没有在雷击发生后重复满足，保护没有误动，如图10所示.

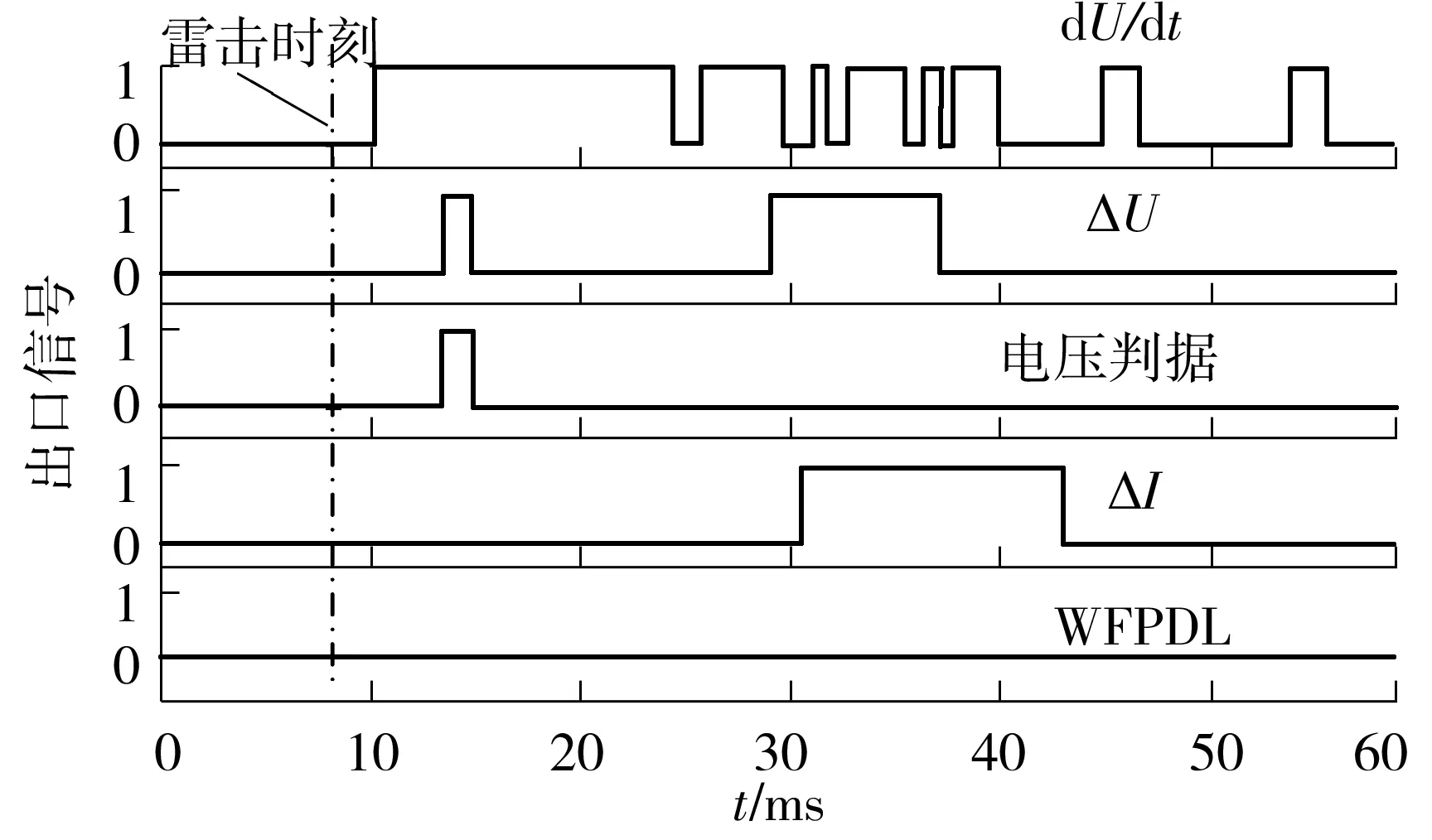
图9 优化后的非雷击线路行波保护特征量响应情况

Fig.9 Protection criteria respective of the non-lightning line of WFPDL after optimization

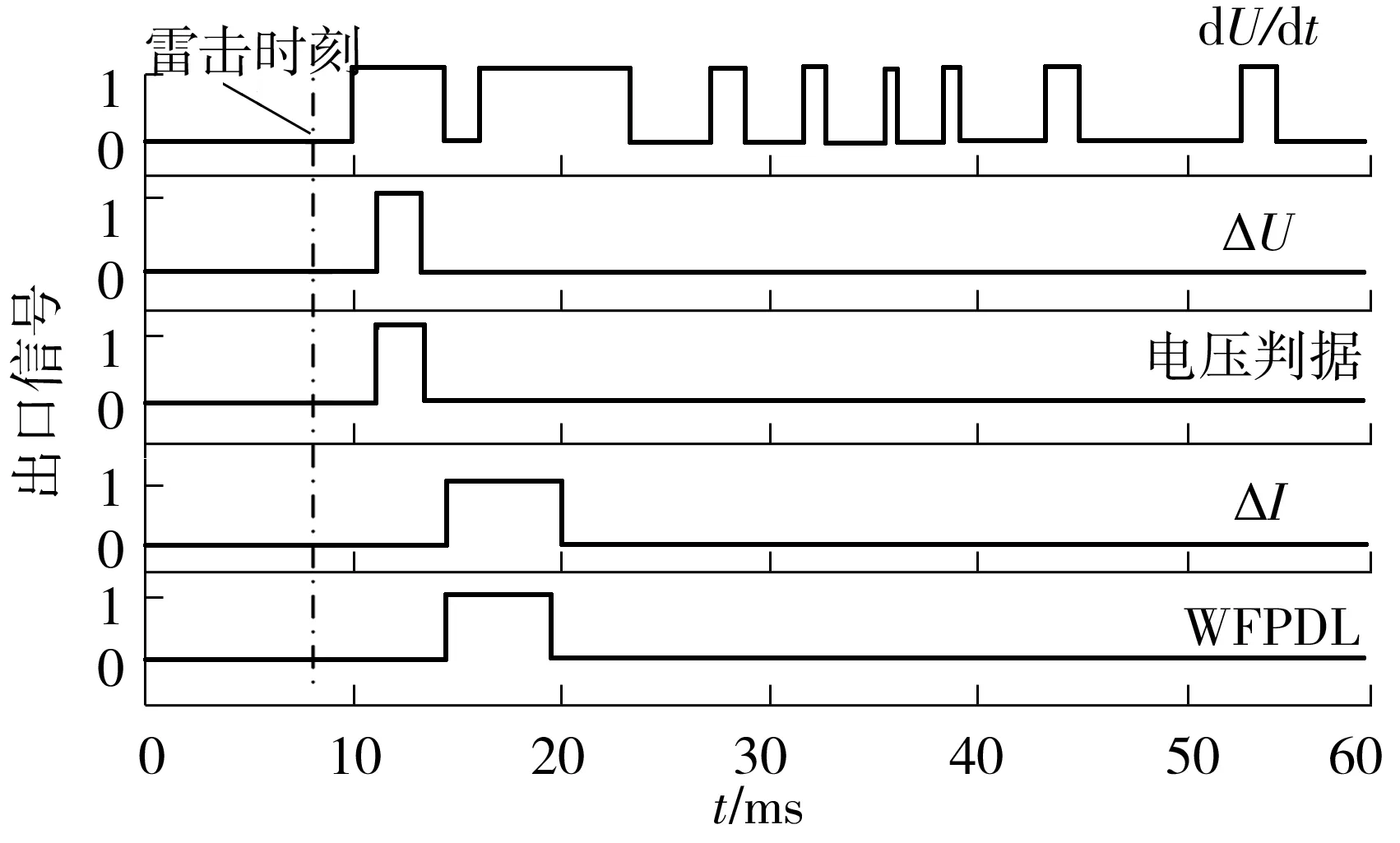
图10 优化后的雷击线路行波保护特征量响应情况

Fig.10 Protection criteria respective of the lightning line of WFPDL after optimization

然后，进一步在优化后的模型中通过改变雷电流的幅值和雷击线路的位置，观察行波保护的动作情况，结果如表3所示.

表3 不同幅值雷电流绕击线路的不同位置时的行波动作情况

Table 3 WFPDL action under different amplitude and location lightning current

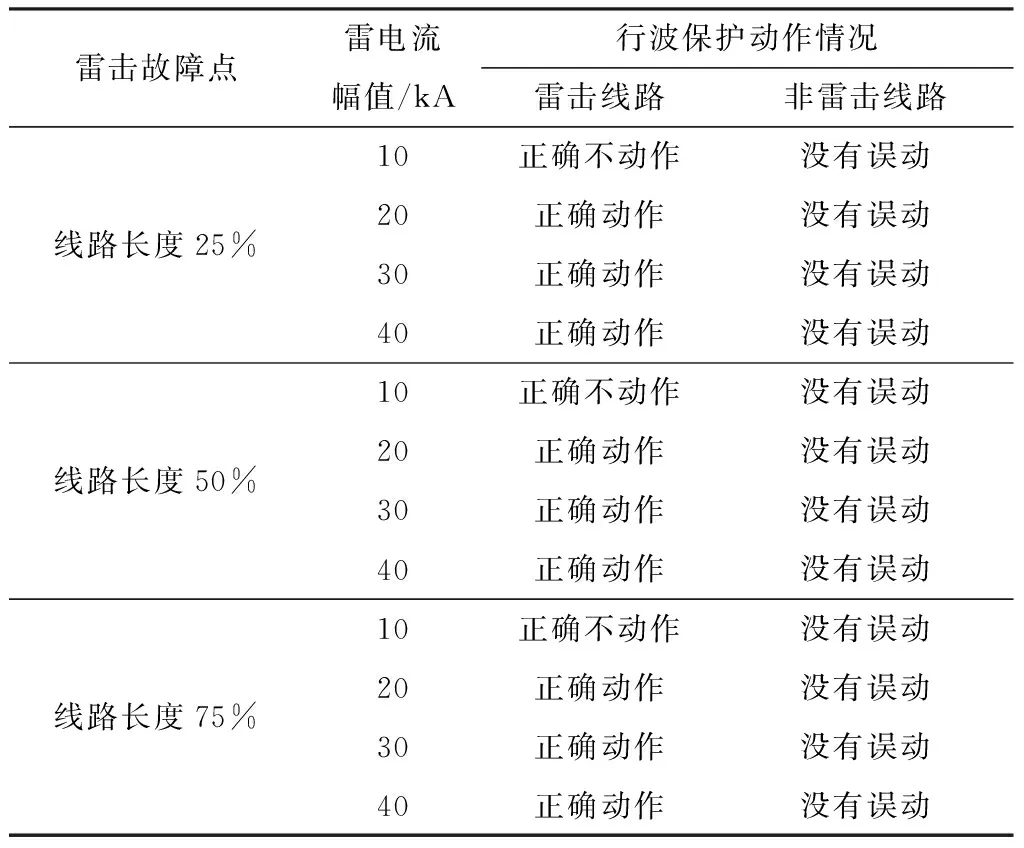
雷击故障点雷电流幅值/kA行波保护动作情况雷击线路非雷击线路线路长度25%线路长度50%线路长度75%10正确不动作没有误动20正确动作没有误动30正确动作没有误动40正确动作没有误动10正确不动作没有误动20正确动作没有误动30正确动作没有误动40正确动作没有误动10正确不动作没有误动20正确动作没有误动30正确动作没有误动40正确动作没有误动

通过上面的仿真结果可以看出，绕击的雷电流在10 kA时雷击线路和非雷击线路的行波保护均没有动作，观察到3个保护特征量没有全部满足幅值条件，同时雷击线路在雷击结束后迅速恢复至正常状态，因此可判断行波保护动作正确.当雷电流达到20 kA以上时，雷击线路行波保护迅速动作，非雷击线路行波保护没有发生误动.

3.3.2 雷击发生后非雷击线路接地故障情况

为了进一步验证所提出的优化策略的可靠性，考虑到在线路一极遭受雷击后，非雷击线路受到来自雷击线路的扰动可能出现在Td时间内行波保护发生闭锁的情况下，如果此时恰好非雷击线路发生接地故障，是否会出现行波保护拒动的情况进而使得直流系统发生闭锁事故.

直流线路发生接地故障的原因是因为污秽或树枝等环境因素造成线路绝缘水平降低而产生的对地闪络.瞬时接地故障的持续时间一般为100 ms以上，远大于行波保护电压判据的闭锁时间Td.因此，在行波保护电压判据闭锁解除后，故障仍未结束，行波保护会正确判断故障并动作.

另一方面，直流线路保护还配置了微分欠压保护和差动保护作为行波保护的后备保护，微分欠压保护的延时在90 ms以上，大于行波保护电压判据闭锁时间Td.由于电压判据的闭锁逻辑没有使特征量的响应情况发生改变，因此，即使行波保护出现拒动，微分欠压保护也会正确动作.

表4 雷电流绕击和接地故障分别作用于直流线路两极时的行波动作情况

Table 4 WFPDL action under location lightning and different position of ground fault

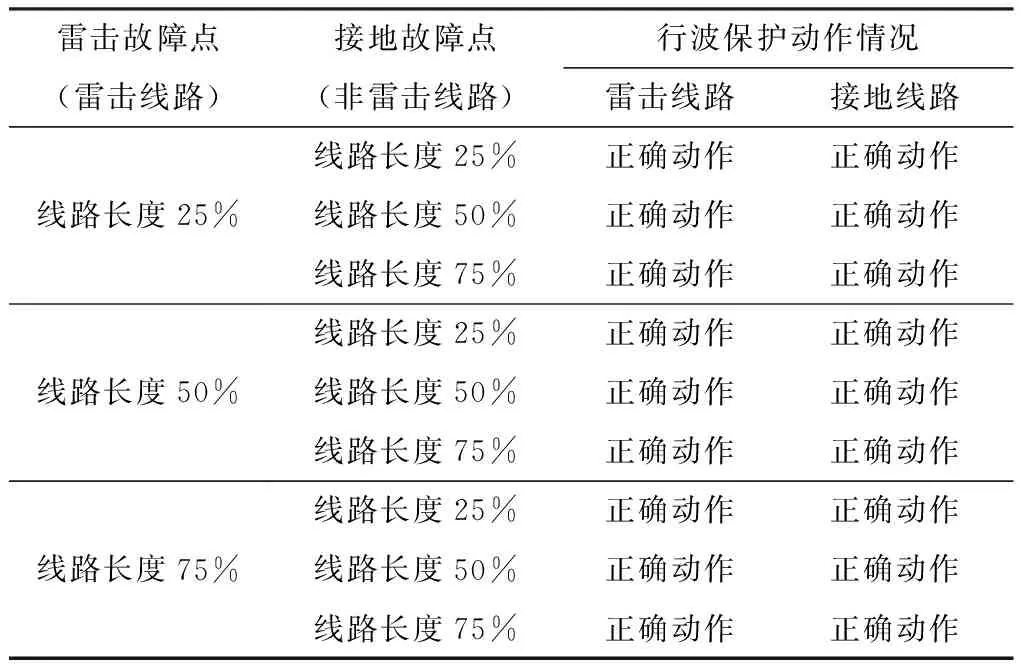
雷击故障点(雷击线路)接地故障点(非雷击线路)行波保护动作情况雷击线路接地线路线路长度25%线路长度50%线路长度75%线路长度25%正确动作正确动作线路长度50%正确动作正确动作线路长度75%正确动作正确动作线路长度25%正确动作正确动作线路长度50%正确动作正确动作线路长度75%正确动作正确动作线路长度25%正确动作正确动作线路长度50%正确动作正确动作线路长度75%正确动作正确动作

基于以上分析，所提的通过增加辅助闭锁逻辑的优化策略本质上是对线路受扰动和真正故障状态下进行区分，闭锁逻辑在故障状态下不起作用，能有效改善非雷击线路行波保护的误动情况，同时并没有牺牲保护的灵敏性和速动性.

4 结论

文中以实际直流工程为背景，正确建立了特高压直流线路雷击模型，分析了非雷击线路行波保护误动情况下的线路暂态过程.基于此，从保护特征量的响应和时序逻辑配合上阐述了非雷击线路行波保护误动的原理，并在此基础上提出了不牺牲行波保护灵敏性和速动性的电压判据优化方法，得出以下结论：

(1)在雷电流绕击直流线路一极时，由于线路间的电磁耦合，非雷击线路会感应出相应的电气突变量可能使得非雷击线路的行波保护特征量满足其对应的门槛值.

(2)直流系统在遭受雷击后，在非雷击极受扰恢复过程中，非雷击线路行波保护特征量多次满足门槛值并恰好满足特征量间既定的延时逻辑关系是行波保护在对极故障发生数十毫秒后误动的重要原因.

(3)通过计算故障行波的传递以及直流控制系统的响应时间，提出在现有电压判据处理方式的基础上，引入时长Td=35 ms的辅助闭锁逻辑，可以防止电压判据在雷击后多次错误出口，能有效改善行波保护的误动情况.

[1] 饶宏，张东辉，赵晓斌，等.特高压直流输电的实践和分析 [J].高电压技术,2015，41(8)：2481- 2488.

RAO Hong,ZHANG Dong-hui,ZHAO Xiao-bin,et al.Practice and analyses of UHVDC power transmission [J].High Voltage Engineering,2015,41(8)：2481- 2488.

[2] 马为民，樊纪超.特高压直流输电系统规划设计 [J].高电压技术，2015，41(8)：2545- 2549.

MA Wei-min,FAN Ji-chao.Planning and design of UHVDC transmission system [J].High Voltage Engineering,2015,41(8)：2545- 2549.

[3] 梁旭明，张平，常勇．高压直流输电技术现状及发展前景 [J]．电网技术，2012，36(4)：1- 9．

LIANG Xu-ming,ZHANG Ping,CHANG Yong.Recent advances in high-voltage direct-current power transmission and its developing potential [J]．Power System Technology,2012，36(4)：1- 9．

[4] 张文亮，汤涌，曾南超．多端高压直流输电技术及应用前景 [J]．电网技术，2010，34(9)：1- 6．

ZHANG Wen-liang，TANG Yong，ZENG Nan-chao．Multi-terminal HVDC transmission technologies and its application prospects in China [J]．Power System Technology，2010，34(9)：1- 6．

[5] 李书勇，郭琦，崔柳，等.特高压直流输电线路雷击暂态过程与行波保护响应特性分析 [J].电网技术,2015，39(10):2830- 2835.

LI Shu-yong,GUO Qi,CUI Liu,et al.Thunderstruck transient process of UHVDC transmission line and response characteristic of traveling wave protection [J]．Power System Technology，2015,39(10):2830- 2835．

[6] 隋国平.云广特高压直流输电线路双极闭锁时安稳装置的动作分析 [J].高电压技术,2012,38(2):421- 426.

SUI Guo-ping.Power safe system analysis of ±800 kV Yun-Guang UHVDC when bipole blocking [J].High Voltage Engineering，2012,38(2):421- 426.

[7] 李书勇，郭琦，韩伟强,等，云广直流“6·5”行波保护动作RTDS仿真分析 [J].南方电网技术，2011,5(z2):47- 50．

LI Shu-yong，GUO Qi，HAN Wei-qiang,et al.RTDS analysis of “6·5”RTDS wave protection trip in Yunnan-Guangdong DC transmission system [J]．Southern Power System Technology，2011,5(z2):47- 50．

[8] 李爱民，蔡泽祥,任达勇，等.高压直流输电控制与保护对线路故障的动态响应特性分析 [J].电力系统自动化，2009,33(11):72- 75.

LI Ai-min，CAI Ze-xiang，REN Da-yong,et al.Analysis on the dynamic performance characteristics of HVDC control and protections for the HVDC line faults [J]．Automation of Electric Power Systems，2009,33(11):72- 75.

[9] 李爱民，蔡泽祥，李晓华，等.高压直流输电线路行波保护影响因素分析及改进 [J].电力系统自动化，2010,34(10):76- 80.

LI Ai-min，CAI Ze-xiang，LI Xiao-hua,et al.Analysis on influence factors and improvement of traveling wave protections for HVDC line [J]．Automation of Electric Power Systems，2010,34(10):76- 80.

[10] 王祎菲，仇一凡，冯世涛，等.雷电流特性及其波形分析 [J].黑龙江电力，2010,32(6)：404- 407.

WANG Yi-fei,QIU Yi-fan,FENG Shi-tao,et al.Chara-cteristics and wave form analysis of lightning current [J].Heilongjiang Electric Power,2010,32(6)：404- 407.

[11] 石光其，方厚辉.雷电电流数学模型的仿真分析 [J].湖南工程学院学报,2004,14(2):14- 16.

SHI Guang-qi，FANG Hou-hui．Simulation and analysis of lighting current mathematic models [J]．Journal of Hunan Institute of Engineering，2004，14(2):14- 16．

[12] 邓军，肖遥，楚金伟，等.±800 kV云广特高压直流线路合成电场仿真计算与测试分析 [J].电力自动化设备，2015,35(2):138- 144.

DENG Jun，XIAO Yao，CHU Jin-wei,et al.Simulative calculation and measurement analysis of total electric field for ±800 kV Yunnan-Guangzhou UHVDC transmission lines [J] ．Electric Power Automation Equipment，2015,35(2):138- 144.

[13] 董杏丽，葛耀中，董新洲.行波保护中雷电干扰问题的对策 [J].中国电机工程学报，2002,28(9):75- 79.

DONG Xing-li，GE Yao-zhong，DONG Xin-zhou．Effect of lightning on protection ased on travelling waves [J]．Proceedings of the CSEE，2002,28(9):75- 79．

[14] 韩昆仑，蔡泽祥，贺智,等.高压直流输电线路故障行波传播特性及其对行波保护的影响 [J].电力系统保护与控制，2013,41(21):20- 25.

HAN Kun-lun,CAI Ze-xiang,HE Zhi,et al.Propagation characteristic of fault traveling wave on HVDC line and its influence on HVDC line traveling wave protection [J]．Power System Protection and Control，2013,41(21):20- 25．

[15] 郑伟，武霁阳，李海锋，等.特高压直流线路自适应行波保护 [J].电网技术,2015,39(7):1995- 2001.

ZHENG Wei，WU Ji-yang，LI Hai-feng,et al.Research on adaptive gavelling wave based protection for UHVDC transmission line [J]．Power System Technology，2015,39(7):1995- 2001．

[16] 韩昆仑.高压直流输电系统换流器与线路保护动态特性分析与整定研究 [D].广州:华南理工大学,2013.

[17] ELSEROUGI A A，ABDEL-KHALIK A，MASSOUD A，et al．A new protection scheme for HVDC converters against DC-side faults with current suppression capability [J]．IEEE Transactions on Power Delivery，2014，29(4)：1569- 1577．

[18] 莫付江，陈允平，阮江军.架空输电线路雷击感应过电压耦合机理及计算方法分析 [J].电网技术,2005,29(6):72- 77.

MO Fu-jiang,CHEN Yun-ping,RUAN Jiang-jun.Analysis on coupling mechanism and calculation method of lightning induced surge on overhead transmission lines [J].Power System Technology,2005,29(6):72- 77.

[19] 杨光亮，邰能灵，郑晓冬，等.±800 kV特高压直流输电控制保护系统分析 [J].高电压技术, 2012，38(12):3277- 3283.

YANU Guang-liang，TAI Neng-ling，ZHENG Xiao-dong,et al．Discussion of ± 800 kV UHVDC transmission control and protection system [J]．High Voltage Engineering，2012，38(12):3277- 3283.

[20] 刘剑，邰能灵，范春菊，等.柔性直流输电线路故障处理与保护技术评述 [J].电力系统自动化,2015，39(20):158- 167.

LIU Jian，TAI Neng-ling，FAN Chun-ju，et al．Comments on fault handling and protection technology for VSC-HVDC transmission lines [J]．Automation of Electric Power Systems，2015，39(20):158- 167.