基于混沌Hamilton振子的QAM接收机设计与实现

陈利民，付永庆

(哈尔滨工程大学 信息与通讯工程学院，哈尔滨 150001)

基于混沌Hamilton振子的QAM接收机设计与实现

陈利民，付永庆

(哈尔滨工程大学 信息与通讯工程学院，哈尔滨 150001)

引入时空混沌Hamilton振子，该振子具有呈平面多吸引子分布，且吸引子之间的轨迹互不干扰.为实现基于混沌Hamilton振子的多进制数字通信，引用区域分割思想. 根据初值映射方法，提出了多进制数字信息的混沌调制系统和解调系统的理论模型.设计了混沌Hamilton振子QAM接收机，并为验证该接收机的性能设计了QAM发射机.整个混沌Hamilton振子通信系统主要由基带调制、射频调制、天线、射频解调、区域分割解调等单元组成.硬件采用FPGA开发平台完成调制、解调算法，软件采用Verilog语言进行编程.完成基于混沌的Hamilton振子的发射机和接收机系统硬件设计，并对设计的结果、性能进行验证.

混沌通信；Hamilton振子；多进制通信； 区域分割；接收机；FPGA

在传统通信系统中，发往信道的模拟采样信号是正弦信号的加权和并且是线性的，然而在混沌通信系统中，其信道采样信号为混沌波形的片段并且是非线性的.混沌信号的这种非线性，不稳定并且非周期的特点使得其在通信上的应用具有众多优势.

混沌参数调制方式利用了混沌的初值敏感性，即差别细微的不同初值会对混沌系统的动力学行为造成很大的、不可预测的影响，通常在混沌振子的相轨迹上可以表现出不同的迁徙状态它们的轨道将很快变得互不相关，这使得混沌信号具有长期不可预测性和抗截获能力.

在通信技术方面，混沌信号的非周期性连续带宽频谱，类似噪声的特性，使它在保密通信方面显示出得天独厚的优越性.同时混沌系统本身又是确定性的，由非线性系统的方程、参数和初始条件完全确定，因此又使得混沌信号易于产生和复制.因此，可以利用相轨迹呈现出不同状态来表示不同的初值信息，从而实现了数字信息到混沌振子的调制[1].

混沌信号的隐蔽性、不可预测性、高复杂度和易于实现都特别适用于保密通信.

本文将Hamilton振子应用于多进制数字通信，采用非常普及的多进制数字通信，目的是与常规多进制通信方式相比较，无需混沌同步，在保证具有保密性的同时提高信息的传输速率和频带利用率.

1 混沌Hamilton振子通信系统模型

1.1 混沌Hamilton振子数学理论模型

Hamilton振子属于时空混沌模型，其数学表达式由如下映射表示：

xk+1=xk+f(yk)

yk+1=g(xk+1)+yk

(1)

其中：f和g的取值是任意的，当f和g取值对称时，其混沌振子相轨迹是对称的.在f()=g()=psin()，p=0.1时，并进行坐标变换后，其相轨迹如图1所示.

从图1可以看出，Hamilton振子的相轨迹由多个分布在不同区域的细胞流组成.细胞流内部形成闭环，之间互不干扰，且都分布在同一平面上，适合混沌多进制调制.具备多吸引子，且分布在同一个平面上， Hamilton模型相轨迹呈平面分布，自由度大，算法实现简单.选用Hamilton振子实现混沌多进制调制解调[2].

图1 Hamilton模型局部细胞流相轨迹

Hamilton振子相轨迹由多个指纹区域组成，指纹区域间由于其规则整齐的分布可以由边界线区分开来；每个指纹区域由一组环状相轨迹(环集)组成，而环集是由初值对Hamilton振子迭代得到，因此可以利用指纹区域携带数字信息，并建立初值与环状相轨迹与指纹区域的映射关系，以此进行混沌多进制数字信息调制.进一步通过建立M进制信息与Hamilton振子初值(决定其相轨迹处于该子区域的初值)的对应关系[3]，即可实现数字信息对Hamilton映射的调制.

Hamilton振子相轨迹是围绕其中心的一条近似圆形环线，且全部落入了某方形子区域内，因此，为降低其计算复杂度，可将Hamilton振子的单环相轨迹用圆环线近似为：

u(t)=J+Acos(2πf0t)

v(t)=K+Asin(2πf0t)

(2)

其中：J，K∈±0.5,A为0.25.分别为圆形相轨迹中心点的横、纵坐标.A为圆线相轨迹的半径.取f0为M进制数字信号的符号速率，设置f0=10KB/s，保证在每一个数字符号周期内生成一个完整的圆形相轨迹.此时，Hamilton振子调制的基带信号带宽Bω=f0.

1.2 混沌Hamilton振子通信系统理论实现模型

采用Hamilton振子简化处理模型进行通信系统的设计带通调制采用4QAM的调制方式.

混沌通信系统框图设计框图如图2.原始数字多进制信息调制到Hamilton振子的相空间的子区域中，完成数字多进制信息的混沌调制，其中包括数字多进制信息到Hamilton振子的初值映射.射频调制模块功能是将混沌基带连续时间多进制信号用较高的载波进行发送传输.接收机接收到的发射信号首先要进行射频解调，其主要功能是对混沌通信系统发射信号进行降频.混沌基带多进制解调模块主要功能是对射频解调后的基带混沌信号进行解调，以恢复出原始多进制信号.区域分割器解调Hamilton振子相空间子区域信息，恢复出原始信号.

图2 基于Hamilton振子的四进制混沌通信系统框图

2 混沌Hamilton振子发射机设计

2.1 基带信号的调制

原始二进制数据源经过串并转换变为四进制信息，用四进制信息驱动混沌模型得到混沌基带信号，对Hamilton振子进行离散化处理后，运用DDS得到两路进行信号的调制[4]，之后进行数据锁存和D/A转换，经差分放大后外接低通滤波器，得到要求的两路模拟基带信号.

由FPGA产生的信号为两路正交的数字基带模拟信号，通过DAC904将数字信号转换成模拟信号，经过OPA690差分放大电路，然后经过低通滤波器输出后，得到四进制混沌Hamilton振子基带调制信号.得到整个Hamilton振子基带信号硬件实现结构如图3所示.

图3 Hamilton振子基带信号硬件实现结构

输出两路Hamilton基带调制信号，分别为坐标系的横纵坐标可得到Hamilton振子四进制的相轨迹图.以I路基带信号、Q路基带信号分别就示波器的Y轴输入端和X轴输入端，构建李萨如图，见图4.这与混沌Hamilton振子模型是一致的.

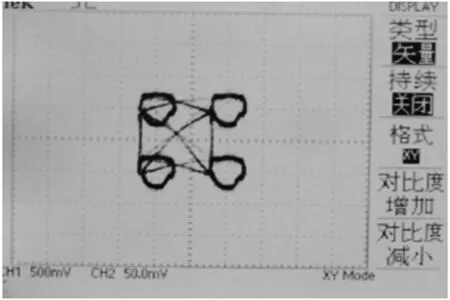
图4 两路混沌Hamilton振子基带调制信号李萨如图

2.2 射频调制模块的设计

根据国家对无线带频谱的管制，144～145 MHz为空闲业余频段，本文选择甚高频VHF频段、米波段进行射频发射，载频为145 MHz.射频发射机的选择ADI公司生产的ADRF6755射频发射芯片来实现，发射机硬件结构如图5所示.

图5 Hamilton振子发射机硬件结构图

FPGA数据输出，使两路DAC904输入基带数字信号，数据经DAC904转换变为基带模拟信号，ADRF6775接入生成的两路混沌Hamilton振子基带信号，完成对载波的调制.天线经过SMA接口与电路板相连，外接天线后接口完成基带信号的射频发射，进而完成射频调制模块的设计.

3 混沌Hamilton振子接收机的设计

3.1 射频解调电路的设计

载波恢复电路采用同相正交环法，即科斯塔斯(costas)环法.ADRF6850集成有costas环，因此可以直接使用芯片完成载波恢复电路的设计.

在FPGA芯片IO口引出SDA和SCL线，通过编程将寄存器数据内容写入ADRF6850芯片[5]，使其按照设定的参数和要求进行工作，完成射频信号的解调工作，得到两路基带模拟信号.

3.2 基带信号采集电路的设计

射频已信号经过ADRF6850解调芯片后，再经过两路低通滤波器，得到两路模拟基带信号[6].为了解调所嵌入的信息，模拟基带信号必须经过区域分割器进行相应的解调工作，首先利用数模转换芯片AD7899将两路模拟基带信号数字化，进一步将数据传入FPGA芯片进行解调处理.

3.3 基带信号解调器的设计

域分割思想是在混沌振子相轨迹上划分区域，以检测相轨迹的相变状态.其划分区域的输出电平可以将二维相图信息转变成一维的时间序列输出，而Hamilton混沌多进制信息是嵌入在Hamilton振子相轨迹所在的指纹区域中，倘若对指纹区域建立区域边界进行划分，通过判断划分的区域内有无环状相轨迹输出不同的电平，则可以实现对Hamilton振子多进制调制信号的解调.

根据区域分割解调思想，完成区域分割解调器的FPGA算法实现，该方法将二维平面轨迹变量转换成一维变量，不仅可以进行实时解调，而且硬件实现简单，无需混沌同步.Hamilton振子接收机硬件实现结构如图6所示.

3.4 混沌Hamilton振子发射机、接收机的整体联调

为了验证整个通信系统的设计的正确性实现与否必须将发射机和接收机同时通电工作，外接天线后，设置接收机的增益[7-9]为60 dB.

将发射机发射的二进制数据，通过接收机解调电路得到的二进制数据对比可知，发射数据和接收数据之间仅有几个时钟的延迟.发射数据与接收数据对比波形如图7所示.

图6 Hamilton振子接收机硬件实现结构

图7 发射数据与接收机数据对比波形

4 结 语

本文以混沌Hamilton振子多进制数字通信作为研究的重点，提出了相应的多进制调制解调方法并进行通信应用，完善了混沌通信技术的相关理论[10-11].根据理论模型，进行混沌Hamilton振子发射机、接收机的设计.验证了Hamilton振子用于混沌通信的可行性、实用性.根据区域分割思想，完成区域分割解调器的FPGA算法实现，在信号解调过程中无需复杂的混沌同步，且在通信中具有较高信息的传输速率、频带利用率和较高的保密性，显示出Hamilton振子在保密通信领域具有强大的生命力.

[1] 禹思敏. 混沌系统与混沌电路[M].西安: 西安电子科技大学出版社, 2011. 10-18.

[2] FU Y, LI X, LI Y,etal. Chaos M-ary modulation and demodulation method based on Hamilton oscillator and its application in communication [J]. Chaos, 2013, 1(23): 013111-013111-12.

[3] 张 芳. 混沌振子多进制调制解调技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. 16-31.

[4] 张春生, 苏开友. 数字信号处理与工程应用实践[M]. 北京: 中国铁道出版社,2013. 149-151.

[5] 韩 彬, 于潇宇. FPGA设计技巧与案例开发详解[M]. 北京: 电子工业出版社, 2014. 459-466.

[6] 段吉海, 黄智伟. 数字通信系统建模与设计[M]. 北京: 电子工业出版社, 2004. 78-80.

[7] 聂春燕. 混沌系统与弱信号检测[M]. 北京: 清华大学出版社, 2004. 19-20.

[8] 邓 洋, 赵民建, 王 匡, 等. QAM 全数字接收机载波相位恢复环路[J]. 电路与系统学报, 2002(2): 105-109.

[9] 杨小牛, 楼才义. 软件无线电技术与应用[M]. 北京: 北京理工大学出版社, 2010. 365-373.

[10] 关新平, 范正平, 陈彩莲, 等. 混沌控制及其在保密通信中的应用[M]. 北京: 国防工业出版社, 2002. 23-26.

[11] 顾成虎，袁梦云.七通道360MHz高速采样接收机设计[J].哈尔滨商业大学学报：自然科学版，2016，32(3)：321-325.

Research on design and implementation of QAM receiver based on chaos Hamilton oscillator

CHEN Li-min, FU Yong-qing

(School of Information and Communication Engineering,Harbin Engineering University, Harbin 150001, China)

The spatiotemporal chaos Hamilton oscillator was introduced in this paper, which has planar multiple attractors distribution, and the attractor trajectories between each other. For the realization of the multi-band digital communication based on chaos Hamilton oscillator, ideas of regional segmentation were introduced. The multi-band digital information theory model of the chaotic modulation and demodulation system was put forward based on the initial value mapping method. The Hamilton chaos oscillator QAM receiver was designed, and to test and verify the performance of the receiver QAM transmitter was also designed. The chaotic communication system consists of baseband modulation, RF modulation, antennas, RF demodulation and regional segmentation demodulation unit. Modulation and demodulation algorithms were implemented on FPGA, while Verilog was used as the programming language. The transmitter and receiver system hardware design were finished based on chaotic Hamilton oscillator, and results and performance of the design were validated.

chaos communication; Hamilton oscillator; multi-band communication; region segmentation; receiver; FPGA

2015-12-03.

国家自然科学基金(61172038)

陈利民(1989-)，硕士,研究方向：通信与信息系统.

TN851

A

1672-0946(2017)01-0077-05