基于混合分块DMICA-PCA的全流程过程监控方法

江伟，王振雷，王昕

(1化学工程联合国家重点实验室，华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237；2上海交通大学电工与电子技术中心，上海 200240)

基于混合分块DMICA-PCA的全流程过程监控方法

江伟1，王振雷1，王昕2

(1化学工程联合国家重点实验室，华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237；2上海交通大学电工与电子技术中心，上海 200240)

分块策略被广泛运用于全流程过程监控领域，以解决全流程过程变量关系复杂性较高的问题，但传统的分块策略与子块建模方法都未考虑过程的动态性问题，并且传统的分块策略都片面依赖于过程知识或过程数据信息，影响了过程监控的效果，为此提出了一种基于混合分块DMICA-PCA的过程监控方法。在分析过程的动态性后，先利用已知的部分过程知识进行变量的初步分块，接着利用各分块变量之间改进的广义Dice's系数(MGDC)进行进一步的分块。然后采用DMICA-PCA方法对每个子块进行建模得到子块的统计量，并通过加权方法得到总的联合指标进行故障检测。同时对每个子块采用改进的故障诊断方法，提高了诊断效果。最后将该方法应用在TE过程的过程监控中，证明了该方法的有效性。

主元分析；过程控制；过程系统；混合分块；全流程；改进的广义Dice's系数

引 言

随着现代工业生产过程对产品质量和安全性的要求日益提高，过程监控正在起着越来越关键的作用[1-2]。其中，基于多变量统计过程监控(multivariate statistical process monitor, MSPM)的方法是过程监控领域的研究热点[3-4]。而在所有的MSPM方法中，主元分析(principal component analysis, PCA)是一种被广泛运用的方法[5-6]，它能对过程数据进行有效降维，并消除了变量之间的相关性，从而获得较好的过程监控效果，但该方法仍存在着不能提取过程数据非高斯信息的问题。为此，基于独立成分分析(independent component analysis, ICA)的过程监控方法被提出[7]，该方法不仅能够提取过程数据的非高斯信息，还能提取过程数据的高阶统计量信息[8]。但是，对于具有多个操作单元、大量过程变量、变量关系复杂等特点的全流程过程来说，这些传统的MSPM方法都不能实现有效的监控[9]。

为了克服全流程过程变量关系复杂性较高的问题并提取全流程过程数据的局部变量信息，提高过程监控效果，分块方法被提出[10-11]。Westerhuis等[12]和Cherry等[13]分别提出了多块PCA与多块PLS及其改进的全流程过程监控方法，这类方法虽然提高了全流程过程的监控效果，但这些分块方法过于依赖过程知识，不能应用于对过程知识了解不足的全流程过程。为此，基于数据驱动的分块方法被提出，Ge等[14]和衷路生等[15]首先提出了一种基于分布式PCA的全流程过程监控方法，将在同一主元方向上贡献度高的变量自动划分在同一子块中。然而基于分布式PCA的分块方法只考虑了过程变量的均值与方差信息，却忽视了变量的其他概率分布信息，影响了子块的监控效果。为此Jiang等[16-17]又先后提出了基于变量之间的Hellinger距离(Hellinger distance, HD)或者互相关信息(mutual information, MI)进行分块的办法，考虑了变量之间的概率分布信息，降低了子块变量之间的非线性关系，提高传统MSPM方法对每个子块的监控效果。另外，针对全流程过程数据分布的特点，Wang等[18-19]提出了利用过程数据的PCA建模后的负荷矩阵P和ICA建模后的混合矩阵W的信息进行分块，分别提高了对变量数据高斯和非高斯分布的全流程过程监控效果。然而这些分块方法都是假设某一时刻的观测数据与过去时刻的观测数据序列无关，即过程是静态的。但是在实际复杂工业过程特别是化工过程中过程变量普遍存在动态关系，即某些变量现在的观测数据与其他变量的过去时刻的观测数据具有相关性，如果在分块与建模中不考虑这一问题，往往得不到好的监控效果，如文献[20]说明对于简单的化工过程，考虑其动态性进行过程监控的效果要更好，而对全流程过程则更需要考虑其动态特性。另外，大部分的全流程过程都能知道部分过程知识，如果在分块中只考虑变量数据信息而不考虑这部分过程知识信息，将有可能导致许多过程上毫不相关的变量被划分到一个子块中，进而影响子块的监控效果。

为此，本文提出了一种基于混合分块动态改进的ICA(dynamic modified ICA,DMICA)-PCA的全流程过程监控方法。在确定全流程过程的具体时滞后，首先根据已知的过程知识进行第一次分块，然后根据各分块变量数据之间改进的广义Dice's系数(modified general Dice's coefficient, MGDC)进行进一步的分块。为了解决过程的动态性以及过程数据存在的高斯与非高斯混合分布的问题，本文对各子块采用DMICA-PCA方法进行建模，获得每个子块的统计量，并对每个子块的统计量进行加权得到总的联合指标实现对实际工业过程的在线监控。另外，本文将采用改进的主元方向贡献度方法进行故障诊断。最后，通过TE过程的仿真实验说明所提方法的有效性。

1 过程的动态性分析

在传统的过程监控方法中，各变量被认为在时间上不相关。然而，在许多化工过程中，由于产品生产流程较长，过程变量之间普遍存在着动态关系，即某些变量与其他变量存在时间上的延迟。如果在对全流程过程的分块与建模过程中不考虑这一特性，将会影响过程监控的效果。为了解决这一问题，本文通过分析过程动态性得到过程的时滞值τ。在确定过程的时滞后，对过程变量进行分块与建模时，都需要考虑当前时刻以及过去τ时刻内的数据信息，以此消除过程的动态性问题，为此每个变量x可以扩展为x(τ)

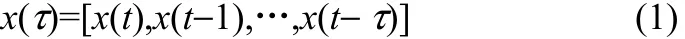
其中，本文采用平行分析法来计算时滞值τ，具体公式见文献[21]。

2 分块方法

传统的分块方法只考虑了当前时刻变量之间的相关关系进行分块，而对于动态过程则需要考虑变量的当前时刻与过去时刻的相关关系进行分块。并且为了解决传统分块方法完全依赖于过程知识导致应用对象不具有普遍性，或完全依赖于数据驱动而造成子块变量过程不相关的问题。本文提出了混合分块的策略，先利用已知的部分过程知识进行分块，接着利用变量数据之间的MGDC值进行进一步的分块。

2.1 基于过程知识的分块方法

对于大部分全流程过程，都可以知道其部分过程知识，本文利用已知的部分过程知识，特别是生产过程及装置的过程知识对原有的过程变量进行分块。因此，对于给定的数据集X(X∈RN×m，其中N为采样个数，m为变量个数)，可以根据过程知识将其首先分块为

2.2 基于MDGC的分块方法

为了进一步降低全流程过程的复杂性，并解决按照部分过程知识进行分块存在的不足，需要对分块后的过程变量进行进一步的分块。主要对各变量之间的MGDC进行子块的划分，GDC是衡量两变量相似性的系数，具体两变量xr与xq之间的GDC值为[22]

而对于动态全流程过程需要考虑变量与其他变量的过去时刻的相关性，因此第k个分块Xk(Xk∈RN×mk)中的变量xkr与其他任意变量xkq的MGDC值为

式中，考虑到了时滞τ的影响。而对分块中各变量之间的MGDC值计算，可以得到一个矩阵Qk

透过矩阵Qk值的分析可以对分块中的变量进行进一步的分块，本文采用K均值聚类的方法，通过对矩阵Qk进行K均值聚类[23]，可以将数据集Xk进一步分为

另外，由于对过程知识不能完全了解，基于部分过程知识进行分块后，不同分块中的变量可能依然存在着相关性，需要根据各变量对其他分块中变量的MDGC值，将系数值较大的变量补充到该子块中，因此最终数据集X可分为

3 建模方法

在对过程变量的分块完成以后，需要对每个子块进行建模获得相应的统计量以及统计监控限，以实现对每个子块的在线监控。为了简化过程监控的步骤，本文通过对子块统计量进行加权得到总的联合指标，并获得相应的统计监控限，以实现对整个全流程过程的在线监控。

3.1 基于DMICA-PCA的建模方法

为了描述每个子块的过程动态信息，在对子块数据进行建模时，需要构建子块的增广矩阵进行建模，对第k个子块Xk(Xk∈RN×mk)来说，其增广矩阵为

本文采用MICA-PCA方法对增广矩阵进行建模，由文献[24]可知该方法可以有效解决过程数据存在的高斯与非高斯混合分布的问题。

其中，lT2和lSPE为相应的统计量T2和SPE的统计监控限，具体公式见文献[27]。通过KDE方法可以得到相应的统计监控限。对MICA统计量和PCA统计量进行加权得到新的统计量，通过KDE方法可得相应的统计监控限，即

3.2 总的联合指标的建立

本文使用一个总的联合指标进行过程监控，定义该指标G2为

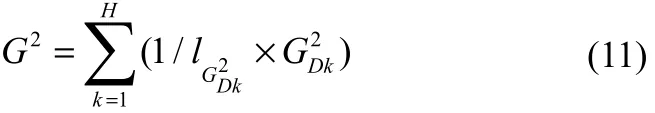
通过对正常工况数据得到的总的联合指标G2进行KDE分析，即可求得总的统计监控限lG2。

4 故障检测与诊断步骤

4.1 故障检测步骤

本文的监控方法可分为离线建模和在线监控，离线建模主要为了获得各子块的统计监控限和总的联合指标的统计监控限，而在线监控主要是为了在线监控系统的运行状态，具体步骤如下。

（1）离线建模

① 首先对正常工况下的样本数据集X∈Rm×n进行均值中心化以及标准化的数据处理。

② 利用平行分析法对标准化后的数据集进行过程动态性分析，得到时滞值τ。

③ 利用已知的部分过程知识对标准化后的数据集进行初步分块，接着利用MDGC方法进行进一步的分块。

④ 采用DMICA-PCA方法对各子块数据集进行建模，得到相应的监控统计量，并计算出子块的统计监控限。

⑤ 对各子块的统计量进行加权得到总的联合指标G2，并计算出联合指标的统计监控限lG2。

（2）在线监控

① 在线获取实时数据，进行数据均值中心化及标准化的数据处理。

② 根据离线建模子块的划分结果，进行子块划分。

③ 计算出各子块的统计量，实施加权后得到总的联合指标，判断是否超限。

4.2 故障诊断步骤

在本文方法中，当故障发生后，各子块将被分为两类：监控效果较好的子块和监控效果较差的子块。因为存在故障相关变量的子块能够提取更多的故障信息，所以与故障相关的变量在监控效果较好的子块中的概率比在监控效果较差的子块中的概率要高。因此可以基于监控效果较好的子块进行故障诊断，该子块中贡献度最高的几个变量即为引起故障或受故障影响的变量。

式中，λ(i)是第i个特征值，pi,j是负荷矩阵P的一个元素。如果有d个失控状态，则第j个变量总的贡献度之和为

由于是对增广矩阵进行主元方向贡献度求解，因此最终第j变量的总的贡献度为

5 TE过程仿真实验

5.1 TE过程

TE过程是由伊斯曼化学公司创建的，其目的是为评价过程控制和监控方法提供一个现实的工业过程。TE过程包括5个主要单元，分别为反应器、冷凝器、压缩机、分离器和汽提塔。该过程包括41个测量变量(包括22个连续测量变量和19个成分测量值)和12个控制变量。TE过程的详细描述可见文献[29]，TE过程的流程如图1所示[30]，图中1～13分别对应于物料流程1～13。TE过程变量数与生产单元数较多，变量之间关系较为复杂，变量还存在着高斯与非高斯混合分布以及非线性相关的问题，另外TE过程还具有动态性问题，该过程较为符合本文所研究的全流程过程特点。文献[14-19]中全流程监控方法都是基于此对象进行研究，因此本文也采用该对象进行相应的仿真研究。

5.2 基于混合分块DMICA-PCA的TE过程仿真

在仿真实验中，首先选取52维的960组正常数据进行标准化处理，之后采用平行分析法获得TE过程的时滞值τ，τ=2。然后计算出各变量与其他变量当前及过去两个时刻数据的GDC值，发现有些变量与其他变量过去时刻数据的GDC值较大，如变量1前一时刻的值与变量44当前时刻值的GDC为0.99(最大为1)，即变量44与变量1前一时刻的相关度较大。因此存在部分变量与其他变量的过去时刻的相关性较高，对TE过程进行分块与建模时需要考虑其动态特性。为此，本文首先根据TE过程已知的部分过程知识，即TE过程已知的生产单元，将与反应器和冷凝器相关的变量、压缩机和分离器相关的变量、汽提塔相关的变量分别划分到3个分块中，具体分块结果如表1所示。为了进一步降低TE过程的复杂性，本文采用MGDC方法对各分块进行进一步的分块，并利用K均值聚类方法将同一分块中MGDC值相近的变量划分到一个子块中，同时为了补充对过程知识了解的不足，将其他分块中与该子块变量的MGDC值较大的变量也添入该子块(如变量7和变量13)，最终的分块结果如表2所示。文献[20]通过J-B检测的方法得出TE过程52个变量中34个变量为高斯分布，18个变量为非高斯分布，而采用文献[24]中的MICA-PCA方法可以有效处理TE过程数据存在的高斯与非高斯混合分布的问题。为了处理TE过程存在的动态性问题，本文则采用DMICA-PCA方法得到各子块相应的统计量与统计监控限，各子块各自的统计监控限分别为1.79、1.89、2、3、1.6。再运用加权方法计算得到总的联合指标并估计出总的统计监控限(3.05)，以此进行TE过程的故障检测。

图1 TE过程流程[30]Fig.1 Flow chart of TE process[30]

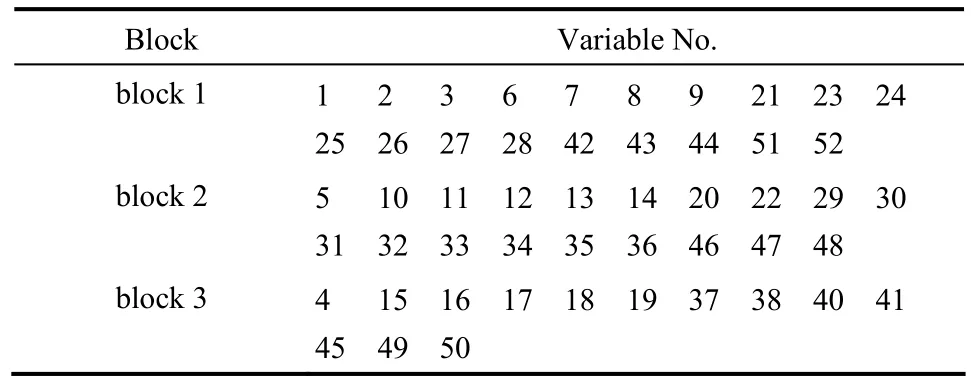
表1 基于部分过程知识的分块结果Table 1 Block results based on partial process knowledge

表2 最终的分块结果Table 2 Final block results

在线监控时，选用960组过程数据进行仿真，故障是在第161个数据时刻引入的。采取本文所用方法得到总的联合指标，并与统计监控限比较，判断其是否超限。经多次实验，得到的检测率与其他方法进行对比，在21种故障中，本文的方法都不差于文献[24]的方法，表3给出了部分故障的检测率对比结果。同时为了证明基于过程动态性进行分块与建模方法的有效性，表3还给出了基于静态混合分块的过程监控方法的检测率，即对利用过程知识分块后的子块基于其GDC进行进一步的分块，并对子块采用MICA-PCA方法进行建模，得到联合指标D2进行监控。由表3可以看出，静态混合分块方法的监控效果要优于传统方法，但本文提出的基于混合分块DMICA-PCA的过程监控方法对于这几类故障要比静态方法有更好的监控效果。

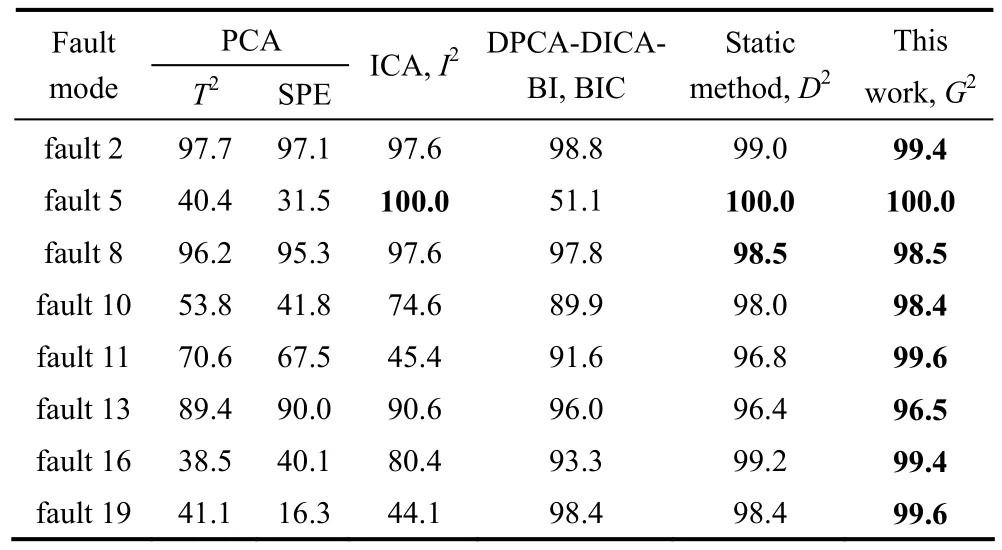
表3 TE过程故障2、5、8、10、11、13、16、19的检测率对比Table 3 Detection rate comparison of fault 2, 5, 8, 10, 11, 13, 16, 19 in TE process/%

故障10是流4段C(图1)的进料温度发生随机波动引起故障，根据表3与图2，可以看出本文的故障检测效果比PCA与文献[24]中的方法都要好。图3给出了故障11部分子块的监控图，除了第5子块的监控效果较好，其他子块的监控效果与图3(a)、(b)类似，因此对该子块进行故障诊断，其他子块的变量的贡献度设为0，得出的结果如图4(a)所示，发现变量4[总进料(流4)]、18(汽提器温度)与故障相关。图4(b)给出的传统方法的诊断结果，可以看出变量3(E进料)、19(汽提器流量)、38(成分E)的贡献度的值最高。而实际上52个变量中与该故障关系最相近的是变量4和18，因此传统方法的诊断效果不如本文的方法。而分布式PCA方法虽然也得出了变量18与故障相关，但是还得出了变量19、变量46(压缩机再循环阀)与故障相关，影响了故障的定位。基于MI的方法的诊断结果为变量18、19与故障相关，同样存在定位困难的问题，因此本文的方法对故障10的诊断效果更好。

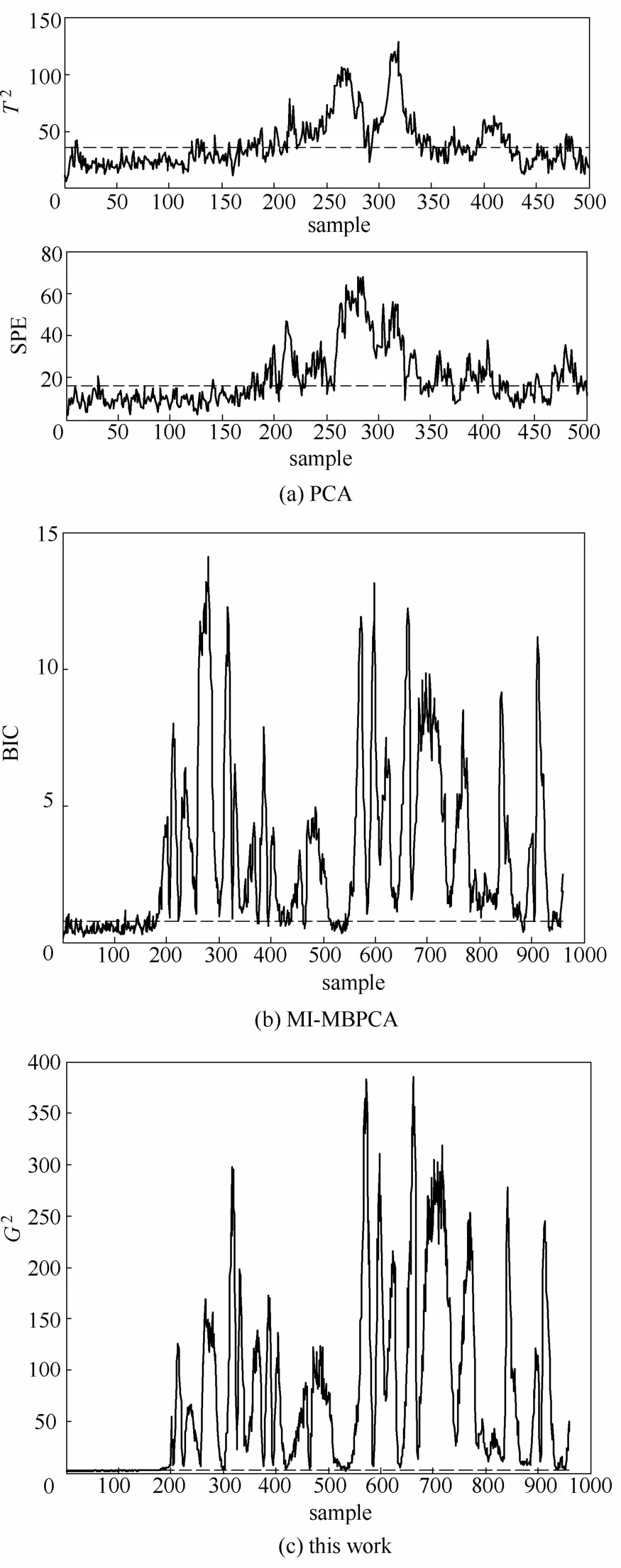
图2 TE过程故障10的监控图对比Fig.2 Comparison of monitoring for fault 10 of TE process

通过TE过程的仿真实验，可以看出本文提出的基于混合分块DMICA-PCA方法，不仅在故障检测效果上优于传统的PCA与ICA及文献[24]的方法，而且本文提出的方法在一些故障中定位故障变量的精确度上要优于传统方法与其他分块方法，因此本文提出的方法对TE过程可以实现较好的监测和诊断。由于本文方法在分块与建模过程中都考虑了过程的动态特性，并采用高斯与非高斯联合指标进行监控，因此本文提出的过程监控方法适合于具有动态特性、数据分布复杂的全流程化工过程的过程监控，由TE过程仿真实验结果可以证明这一特点。

图3 TE过程故障10部分子块的监控图对比Fig.3 Comparison of monitoring of partial sub blocks for fault 10 of TE process

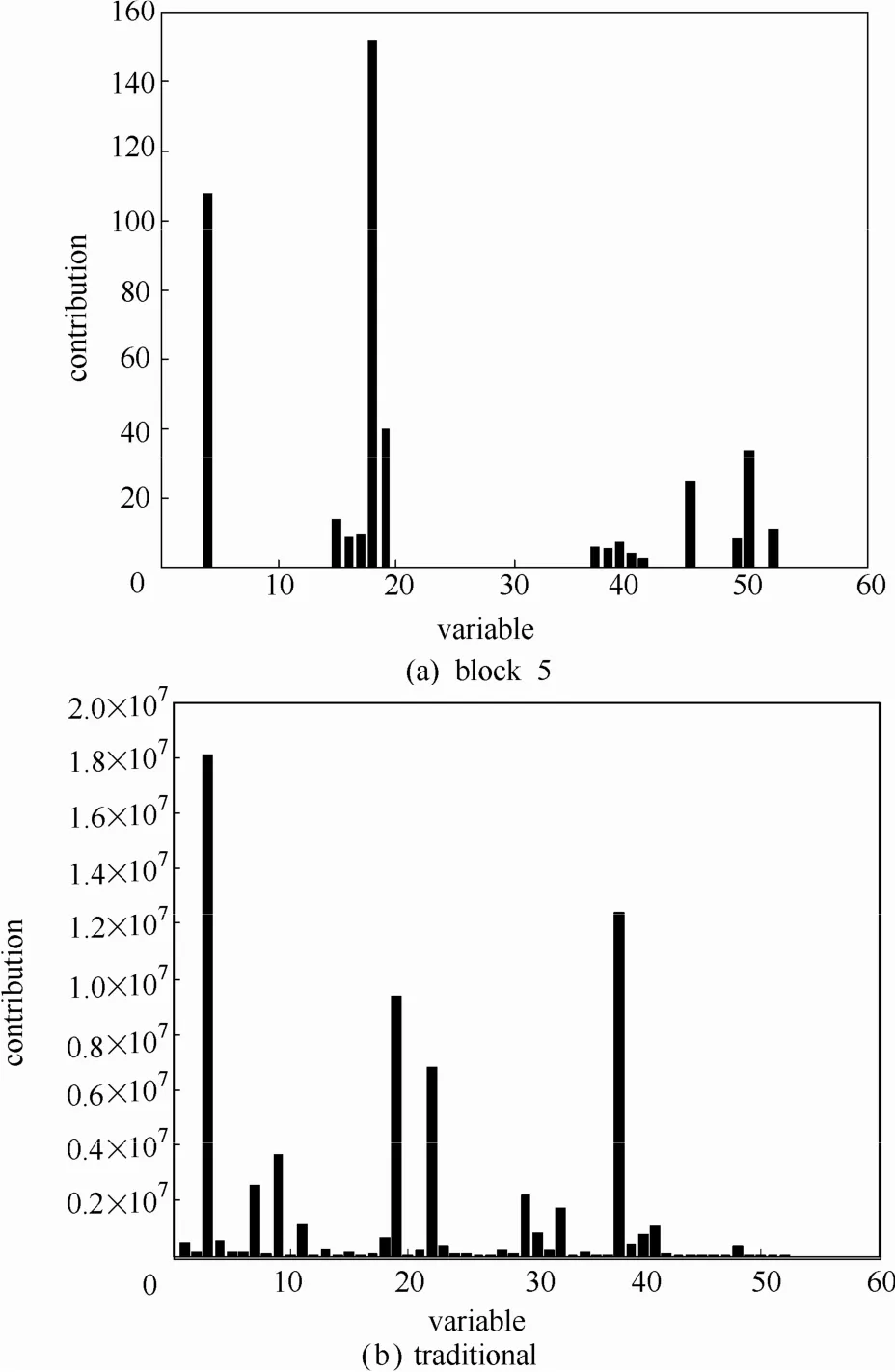
图4 TE过程故障10的贡献图对比Fig.4 Comparison of contribution for fault 10 of TE process

6 结 论

本文提出了一种基于混合分块DMICA-PCA的全流程故障检测与诊断方法，有效地降低了全流程过程的复杂性。该方法利用变量当前时刻的值与其他变量过去时刻的值存在相关性，首先利用平行分析法得到全流程过程的时滞值。接着利用复杂工业过程已知的部分过程知识进行分块，并利用变量之间的MGDC值进行进一步的分块。并通过DMICA-PCA方法对每个子块进行建模，解决了子块数据存在的高斯与非高斯混合分布以及过程变量数据存在的动态性问题。通过构建联合指标进行故障检测，并通过对每个子块进行故障诊断，提高了故障检测与诊断的效果，最后通过对TE过程的仿真实验证明了该方法的有效性。

[1] JIA Q L, ZHANG Y W. Quality-related fault detection approach based on dynamic kernel partial least squares[J]. Chemical Engineering Research and Design, 2016, 106: 242-252.

[2] WANG T, WU H, NI M,et al. An adaptive confidence limit for periodic non-steady conditions fault detection[J]. Mechanical Systems and Signal Processing, 2016, 72: 328-345.

[3] SONG B, TAN S, SHI H. Process monitoringviaenhancedneighborhood preserving embedding[J]. Control Engineering Practice, 2016, 50: 48-56.

[4] LI N, YANG W, YANG Y. Spatial-statistical local approach for improved manifold-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2015, 54(34): 8509-8519.

[5] LI W, YUE H H, VALLE C S,et al. Recursive PCA for adaptive process monitoring[J]. Journal of Process Control, 2000, 10(5): 471-486.

[6] 童楚东, 史旭华. 基于互信息的 PCA 方法及其在过程监测中的应用[J]. 化工学报, 2015, 66(10): 4101-4106. TONG C D, SHI X H. Mutual information based PCA algorithm with application in process monitoring[J]. CIESC Journal, 2015, 66(10): 4101-4106.

[7] HYVARINEN A, OJA E. Independent component analysis: algorithms and applications[J]. Neural Networks, 2000, 13(4): 411-430.

[8] ZHANG Y W, ZHANG Y. Fault detection of non-Gaussian processes based on modified independent component analysis [J]. Chemical Engineering Science, 2010, 65: 4630-4639.

[9] WANG B, JIANG Q C, YAN X F. Fault detection and identification using a Kullback-Leibler divergence based multi-block principal component analysis and bayesian inference[J]. Korean Journal of Chemical Engineering, 2014, 31(6): 930-943.

[10] MACGREGOR J F, JAECKLE C, KIPARISSIDES C,et al. Process monitoring and diagnosis by multiblock PLS methods [J]. AIChE J., 1994, 40: 826-838.

[11] GE Z Q, SONG Z H. Two-level multiblock statistical monitoring for plant-wide processes [J]. Korean J. Chem. Eng., 2009, 26: 1467-1475.

[12] WESTERHUIS J A, KOURTI T, MACGREGOR J F. Analysis of multiblock and hierarchical PCA and PLS models[J]. Journal of Chemometrics, 1998, 12(5): 301-321.

[13] CHERRY G A, QIN S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis[J]. IEEE Transactions on semiconductor manufacturing, 2006, 19(2): 159-172.

[14] GE Z Q, SONG Z H. Distributed PCA model for plant-wide process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(5): 1947-1957.

[15] 衷路生, 何东, 龚锦红, 等. 基于分布式 ICA-PCA 模型的工业过程故障监测[J]. 化工学报, 2015, 66(11): 4546-4554. ZHONG L S, HE D, GONG J H,et al. Fault monitoring of industrial process based on distributed ICA-PCA model[J]. CIESC Journal,2015, 66(11): 4546-4554.

[16] JIANG Q C, WANG B, YAN X F. Multiblock independent component analysis integrated with Hellinger distance and Bayesian inference for non-Gaussian plant-wide process monitoring[J]. Industrial & Engineering Chemistry Research, 2015, 54(9): 2497-2508.

[17] JIANG Q C, YAN X F. Plant-wide process monitoring based on mutual information multiblock principal component analysis[J]. ISA Transactions, 2014, 53(5): 1516-1527.

[18] WANG B, YAN X F, JIANG Q C,et al. Generalized Dice's coefficient based multi-block principal component analysis with Bayesian inference for plant-wide process monitoring[J]. Journal of Chemometrics, 2015, 29(3): 165-178.

[19] WANG B, YAN X F, JIANG Q C. Independent component analysis model utilizing de-mixing information for improved non-Gaussian process monitoring[J]. Computers & Industrial Engineering, 2016, 94: 188-200.

[20] HUANG J, YAN X F. Dynamic process fault detection and diagnosis based on dynamic principal component analysis, dynamic independent component analysis and Bayesian inference[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 148: 115-127.

[21] 钟丽丽. 基于动态主元分析的故障诊断研究[D]. 青岛: 青岛科技大学, 2013. ZHONG L L. Research on fault diagnosis of dynamic principle component analysis[D]. Qingdao: Qingdao University of Science and Technology, 2013.

[22] ZHANG Y, LIU Y, JI Z. Vector similarity measurement method[J]. Technical Acoustics, 2009, 4(5): 532-536.

[23] 张子羿, 胡益, 侍洪波. 一种基于聚类方法的多阶段间歇过程监控方法[J]. 化工学报, 2013, 64(12): 4522-4528. ZHANG Z Y, HU Y,SHI H B.Multi-stage batch process monitoring based on a clustering method [J]. CIESC Journal, 2013, 64(12): 4522-4528.

[24] 江伟, 王昕, 王振雷. 基于 LTSA 和 MICA 与 PCA 联合指标的过程监控方法及应用[J]. 化工学报, 2015, 66(12): 4895-4903. JIANG W, WANG X, WANG Z L. LTSA and combined index based MICA and PCA process monitoring and application [J]. CIESC Journal, 2015: 66(12):4895-4903.

[25] LI X, YANG Y, ZHANG W. Statistical process monitoringviageneralized non-negative matrix projection[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 121: 15-25.

[26] 杨正永, 王昕, 王振雷. 基于 LTSA 和联合指标的非高斯过程监控方法及应用[J]. 化工学报, 2014, 66(4): 1370-1377. YANG Z Y,WANG X,WANG Z L. LTSA and combined index based non-Gaussian process monitoring and application[J].CIESC Journal, 2014: 66(4):1370-1379.

[27] YUE H H, QIN S J. Reconstruction-based fault identification using a combined index[J]. Industrial and Engineering Chemistry Research, 2001, 40(20): 4403-4414.

[28] XIE L, LI Z, ZENG J,et al. Block adaptive kernel principal component analysis for nonlinear process monitoring[J]. AIChE Journal, 2016, 62(12): 4334-4345.

[29] CHIANG L H, RUSSELL E L, BRAATZ R D. Fault Detection and Diagnosis in Industrial Systems [M]. Berlin: Springer, 2001.

[30] JIANG Q C, YAN X F. Probabilistic weighted NPE-SVDD for chemical process monitoring[J]. Control Engineering Practice, 2014, 28: 74-89.

Plant-wide process monitoring based on mixed multiblock DMICA-PCA

JIANG Wei1, WANG Zhenlei1, WANG Xin2
(1State Key Laboratory of Chemical Engineering,Key Laboratory of Advanced Control and Optimization for Chemical Processes,East China University of Science and Technology,Shanghai200237,China;2Center of Electrical & Electronic Technology,Shanghai Jiao Tong University,Shanghai200240,China)

Multiblock strategy is widely used in plant-wide process monitoring to solve problems with complicated relationships between process variables. Traditional multiblock strategies and sub-block modeling methods are not effective in plant-wide process monitoring, because dynamic characteristics of the process have not been considered and knowledge or data information of the process is exclusively exploited. A mixed multiblock DMICA-PCA method was proposed to improve process monitoring performance. First, variables were sliced into initial sub-blocks by obtained process knowledge after analysis of process dynamics and further sliced into final sub-blocks by modified general Dice's coefficient (MGDC) between variables of initial sub-blocks. Then, the DMICA-PCA method was used to establish model and acquire statistical values of variables in final sub-blocks and a combined overall index from weighted sum was developed for fault detection, which improved performances by simultaneous diagnosis on each sub-block. Effectiveness of the proposed method was validatedon monitoring the Tennessee-Eastman (TE) process.

principal component analysis; process control; process systems; mixed multiblock; plant-wide process; modified general Dice's coefficient

Prof. WANG Zhenlei, wangzhen_l@ecust.edu. cn

TP 277

：A

：0438—1157（2017）02—0759—08

10.11949/j.issn.0438-1157.20161309

2016-09-19收到初稿,2016-12-05收到修改稿。

联系人：王振雷。

：江伟(1991—)，男，硕士研究生。

国家自然科学基金重点项目(61134007)；国家自然科学基金青年项目(61403141)；上海市“科技创新行动计划”研发平台建设项目(13DZ2295300)；上海市自然科学基金项目(14ZR1421800)；流程工业综合自动化国家重点实验室开放课题基金资助项目(PAL-N201404)。

Received data: 2016-09-19.

Foundation items: supported by the Key Program of National Natural Science Foundation of China (61134007), the Youth Program of National Natural Science Foundation of China (61403141), the Shanghai “Technology Innovation Action Plan” Development Platform for Building Projects (13DZ2295300), the Natural Science Foundation of Shanghai (14ZR1421800) and the State Key Laboratory of Synthetical Automation for Process Industries (PAL-N201404).