直觉模糊多核聚类算法及其在乙烯原料属性聚类中的应用

崔兴华，杜文莉，赵亮，李江利，池亮

(1化学工程联合国家重点实验室，华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237；2中国石油天然气股份有限公司吉林石化分公司，吉林省 吉林市 132000)

直觉模糊多核聚类算法及其在乙烯原料属性聚类中的应用

崔兴华1，杜文莉1，赵亮1，李江利2，池亮2

(1化学工程联合国家重点实验室，华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237；2中国石油天然气股份有限公司吉林石化分公司，吉林省 吉林市 132000)

随着乙烯裂解原料种类的日益增多，原料分析仪价格昂贵，因此根据乙烯裂解原料属性进行在线聚类，对实现乙烯收率建模，优化乙烯产率、节能减耗具有重要现实意义。为了提高原料在聚类的准确性，提出了一种基于直觉模糊集理论的核聚类算法。即在定义直觉模糊集隶属度时通过引入犹豫度来表征数据的不确定信息，同时利用直觉模糊熵对多核聚类算法的损失函数重新定义，使类簇中的数据点最优化；进一步地，使用随机森林对裂解原料属性进行特征选择，依据对乙烯产率的贡献度选取聚类的主要特征属性。最后根据实际工业裂解的石脑油数据验证了所述算法的有效性。

算法；熵；优化；直觉模糊；乙烯裂解

引 言

在乙烯生产过程中[1]，乙烯收率不仅受到裂解过程中的操作条件如温度、压力、停留时间等影响，其裂解原料属性也是决定收率的重要因素，然而裂解原料仅石脑油类别就有上百种不同的油品属性，其馏程范围为30～220℃，考虑针对所有不同油品属性进行产率的建模不仅模型规模大，油品属性的频繁变化也导致在线实施困难[2]。因此需要结合工业实际检测指标，然而工业现场提供的密度测定法、馏程测定法等检测指标不能明确裂解原料的组成，其相对应的裂解产物收率无法准确建模，因此对不同裂解原料进行聚类，为每类油品选择能够代表该簇特征属性的聚类中心，并根据代表该簇特征属性的聚类中心选择裂解产率模型[3]，进而调整运行条件。

聚类算法作为非监督的学习方法在识别数据的内在结构方面具有极其重要的作用。聚类算法是根据数据的特征属性，对目标进行分类，致使一个类簇内的数据具有较高相似性，不同类簇之间具有较低的相似性。

在过去数十年间，许多聚类算法被提出，包括k-means[4]、混合模型聚类[5]、谱聚类[6]等聚类。这些方法中的大多数都属于硬聚类，对类别的归属是严格的，只能分配每一个对象单个类簇，对于类簇紧凑，类别明显的数据会产生很好的聚类效果。然而，在现实世界中，类簇之间有重叠，当一个对象属于两个或多个簇时，模糊聚类算法将会取得更好的效果。

模糊C均值聚类算法[7]以算法收率速度快、算法简易能够处理大量数据[8]等优点成为模糊聚类中采用最主要的算法。它定义隶属度，表明数据属于不同类别的程度。然而，就和大多数其他聚类方法一样，模糊C均值聚类算法是基于欧式聚类，在对于球形簇，将会取得较好的效果，而对于更一般的簇，FCM不适宜处理。因此基于核函数[9]的聚类方法被提出，其通过核函数将数据进行非线性映射到高维空间来处理非球形簇问题。文献[10]提出的多核聚类算法用多个核函数进行加权，动态的调整权重使其避免对于特定任务选择核函数的难题[11]。

在实际裂解过程中，乙烯原料特征属性众多，综合分析比较复杂，相关学者针对裂解原料属性[12]存在模糊边界的问题，采用隶属度信息对裂解原料进行了聚类划分，如文献[13]引入了混合概率模型的模糊隶属度设置方法，从而充分利用裂解原料的先验知识进行更加有效的模糊聚类；文献[14]指出由于在工业中石脑油原料组分复杂，油品特性波动大，致使乙烯裂解深度建模精度不高，为解决此问题，采用模糊核聚类对石脑油数据库进行最优划分，同时用最小二乘支持向量机对每个聚类做非线性回归的方法来提高模型精度。文献[15]通过采用一种基于核函数的动态聚类方法，以广义的欧氏距离作为高维特征空间的相似性度量，进而提高聚类的准确性，优化乙烯裂解过程中操作模式。

本文相较于以上算法的创新之处在于，将直觉模糊集[16]应用到多核模糊聚类算法上，提出了直觉模糊多核聚类算法（IKFC）。在以往的模糊聚类算法中，模糊集只定义了隶属度、非隶属度，描述了对象“亦次亦彼”的模糊概念，在缺少先验知识的情况下，隶属度的定义是不准确的，会出现不确定信息。借助于文献[17]提出的直觉模糊集理论，在IKFC算法中引入新的属性参数-犹豫度来表示这种不确定性。使得直觉模糊集在处理具有不确定信息[18]的决策时比传统的模糊集具有更强的表示能力，且更具灵活性。同时在聚类的损失函数上引入直觉模糊熵，降低数据所属类别的不确定性，最优化聚类中的数据点，从而更善于处理乙烯裂解原料中的不确定信息。

在以往对乙烯裂解原料进行聚类时，均是根据先验知识选取影响裂解乙烯产率的原料特征属性，本文提出利用随机森林[19]对乙烯裂解原料属性进行特征选择，将每个特征对乙烯产率的贡献度量化，相对于文献[13-15]的方法，更利于分析哪些特征属性对乙烯产率起主导作用。并且和主成分分析、线性判别分析和逐步回归等特征选择方法相比较，随机森林方法不仅能够将贡献度量化，同时也避免了过拟合的难题。

1 多核模糊聚类算法

1.1 模糊C均值聚类算法

在传统的模糊C均值聚类算法(fuzzy C-means clustering, FCM)中，给定聚类的类别C，数据集X={x1,x2,…,xn} 包含N个l维向量xi。定义隶属度uic表示数据xi属于类别C的能力，最小化目标函数

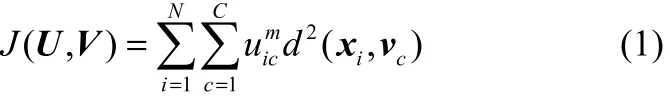
式中，d是欧氏距离；m是隶属度的加权指数，m＞1；Uic是N×C的隶属度矩阵，i=1,…,N;c=1,…,C；vc是聚类中心。

1.2 多核模糊聚类算法

传统的核聚类算法通常使用一个核函数，这样对于特定任务，特定模型需要选用相应的核函数才能很好地处理问题，而如何选择核函数一直是研究的难点，文献[10]提出的多核模糊聚类算法(multiple kernel fuzzy clustering, MKFC)采用多个核函数加权，并动态的调整各个核函数的权重，使其能够聚集成更一般的簇，并解决了核函数[20]选择的难题。定义其损失函数

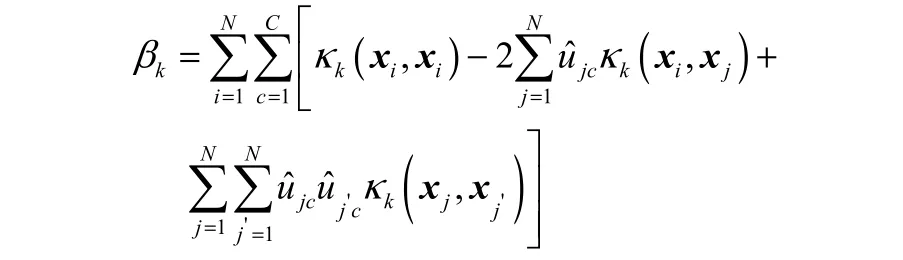
2 直觉模糊多核聚类算法

2.1 直觉模糊集的定义

传统的聚类算法采用的是集合论，集合论只能描述非此即彼的分明概念；在模糊理论[21]中，引入隶属度，从而可以描述亦此亦彼的模糊概念。在直觉模糊集理论增加一个新的属性参数——犹豫度，进而还可描述非此非彼的中立状态[22]，它是对模糊集理论的一种扩充和发展。

定义1(直觉模糊集)：设X是一个给定论域，则X上的直觉模糊集为A={x,uA(x),vA(x)|x∈X}。其中分别表示隶属度uA(x)和非隶属度vA(x)。对于A上x∈X，满足0≤uA(x)+vA(x)≤1。同时定义隶属度函数πA(x)=1-uA(x)-vA(x)，0≤πA(x)≤1。

Pal等[23]分析经典的香农信息论和熵指数，得出对于一个概率分布：p=p1,p2,…,pn，其指数熵定义为。在模糊集中，定义直觉模糊程度。

2.2 构建犹豫度

由Yager[24]生成函数定义：直觉模糊泛函(fuzzy complement functional)

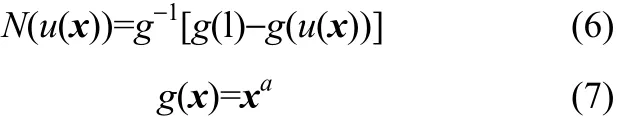
式中，g(·)为增函数。

直觉模糊补集

式中，N(1)=0,N(0)=1。

由式（6）、式（7）、式（8）得出直觉模糊集

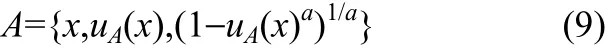
从而确定犹豫度

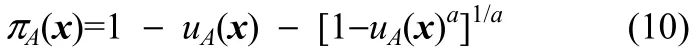
2.3 直觉模糊多核聚类算法

在本文提出的直觉模糊多核聚类算法(IKFC)中，损失函数最小化包含两部分:（1）基于犹豫度多核聚类算法的损失函数；（2）直觉模糊熵。

2.3.1 定义直觉模糊隶属度 犹豫度由式（10）计算得到，则重新定义的直觉模糊隶属度

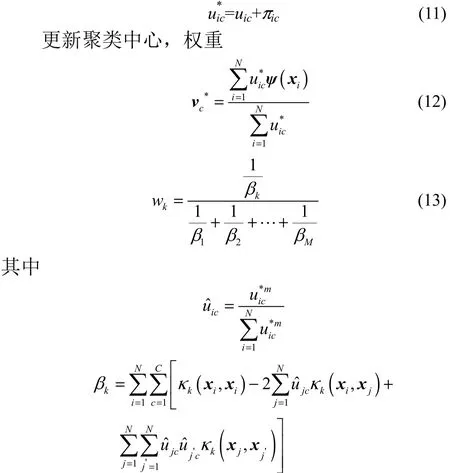
2.3.2 定于犹豫度的熵 犹豫度熵代表的是数据点的不确定程度，引入犹豫度[25]熵的目的是使类簇中的数据点达到最优，不确定性降低。

犹豫度的熵定义为

最终的损失函数定义为

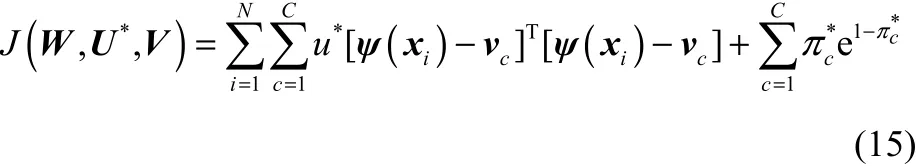
3 随机森林特征选择

3.1 随机森林回归

随机森林（random forest, RF）回归是由Brieman[26]于2001年提出一种集成机器学习方法，它在分类、回归和特征选择方面均被广泛的采用。随机森林方法采用随机重采样(bootstrap)技术和节点随机方法生成多个回归树组成随机森林，生成的随机森林为多元非线性回归分析模型。它可以看成是由很多弱预测器（回归树)集成为强预测器的方法。其特征和数据选取的双重随机性保证了回归树选择的多样性，避免了过拟合的现象。

设数据集X包含N个L维向量xixi，X={x1,x2,…,xN}。随机森林回归算法的流程如下。

（1）采用bootstrap有放回从数据集X中随机抽取n个自助样本集，并由此构建n棵回归树，每次未被抽样的样本组成n个袋外数据(out-of-bag，OOB)。

（2）从L维输入特征中随机挑选l维特征(l＜＜L)，遍历每个特征l，以及每个特征的取值s，计算每个切分点的损失函数如式（16）所示，选择损失函数最小的切分点。得到的切分点将输入空间划分为两部分，递归进行步骤（2），直至不能继续划分。

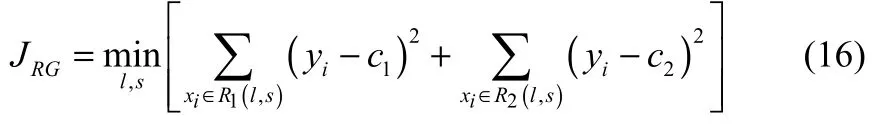
（3）将输入空间划分为m个区域R={R1,R2,…,Rm}生成回归树

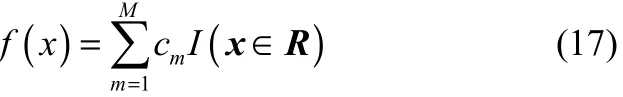
（4）将生成的回归树组成随机森林，采用袋外数据(OOB)残差的均方值和，如式（18）作为预测结果的评价标准。

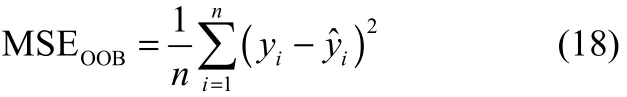
式中，cm为所在区域输出值的平均值；I(·)为指示函数，当括号内成立返回1，否则返回0；yi为袋外数据中目标的实际值；yˆi为随机森林的预测值。

3.2 贡献度评价标准

特征属性对目标值贡献度评分采用Permutation Test[27]方法。Permutation Test的方法是通过将第l维特征的所有数据重新随机调整位置，然后比较原始数据和调整之后数据表现的差距，从而评价这个维度的特征的重要性。

（1）对n个自助样本建立回归模型，并对相应的袋外数据进行预测，得到n个残差均方：MSE1，MSE2，…，MSEn。

（2）特征属性l上的数据在n个袋外数据样本中随机置换，产生新的测试样本，并得到新的袋外残差均方

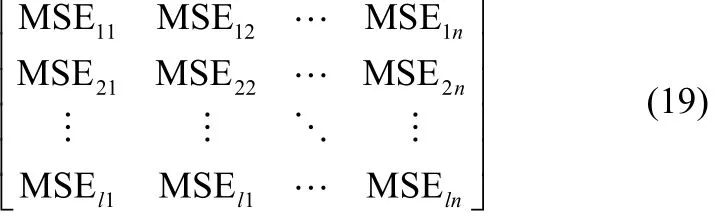
（3）将MSE1，MSE2，…，MSEn与矩阵式（19）对应的第i行相减，取均值后再除以标准误差SE即为特征属性对目标值的贡献度

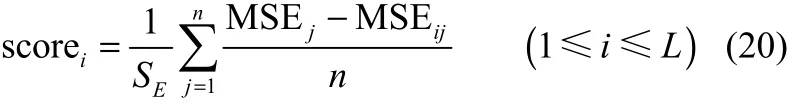
4 仿真实验

为验证IKFC算法对聚类效果的改进及其在乙烯裂解原料中的应用，首先使用经典的Iris和Seeds数据集进行算例比较，之后使用石脑油数据表1作为测试数据，验证算法在实际工业中的应用效果。

4.1 Dunn聚类评价指标

Dunn[28]指标利用簇间距离和簇内直径之比的非线性组合来评价聚类结果。其定义为

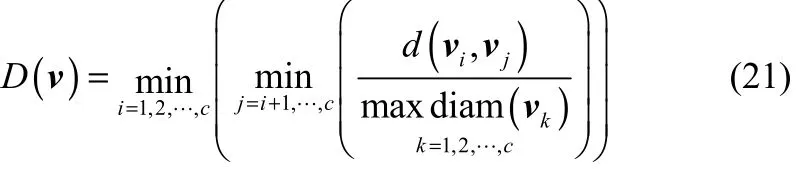
式中，d(vi,vj)表示类vi和类vj之间的距离；表示簇内最大距离，当有紧密分布的数据集中在一个类中，而类与类之间比较分离，那么此时类内直径比小，而类间距离大，根据式（21）表明Dunn指标越大，则聚类效果越理想。

4.2 Iris和Seeds数据集测试

为验证直觉模糊多核聚类算法(IKFC)在聚类效果上的改进，首先使用IKFC算法，模糊C均值聚类算法(FCM)，多核模糊聚类算法(MKFC)在经典的Iris[29]和Seeds[30]数据集上进行算例比较。如图1和图2所示，其中纵坐标Dunn是聚类的评价指标，横坐标m为隶属度的加权指数，随着m值的增大，数据的模糊划分程度越大。

从图1、图2中可看出，在m＞1.35时，IKFC算法在Iris和Seeds数据集的Dunn指标大于FCM算法和MKFC算法的Dunn指标，表明使用IKFC算法进行聚类使得不同类簇的间距变大，簇内直径变小，数据分布更加紧凑，即取得比FCM和MKFC更好的聚类效果。

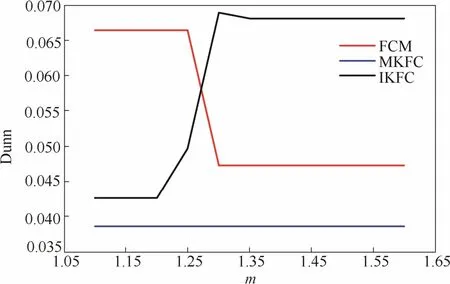
图1 鸢尾花 Dunn数据指标对比Fig.1 Comparison of Iris Dunn index

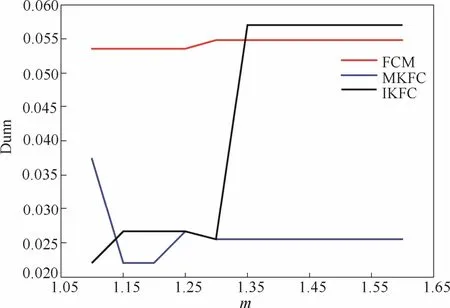
图2 种子 Dunn数据指标对比Fig.2 Comparison of Seeds Dunn index

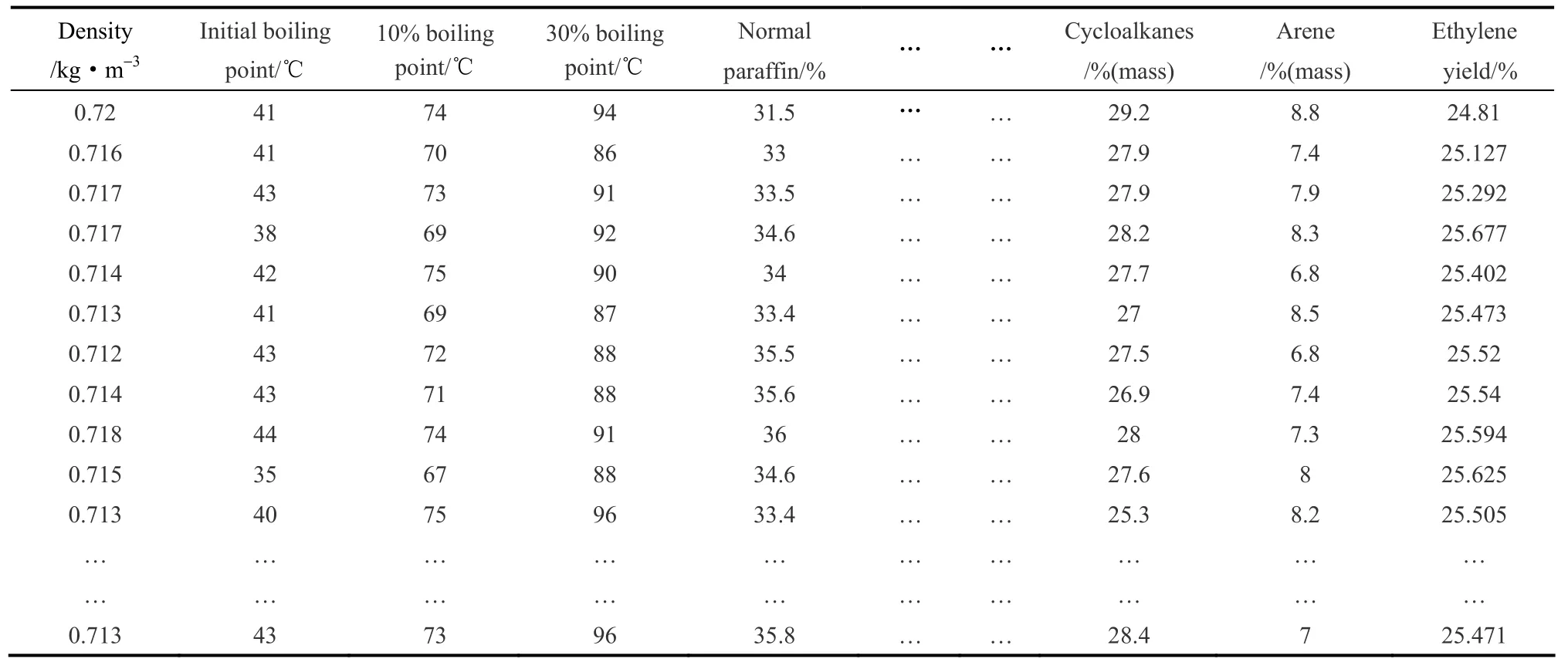
表1 某厂石脑油原料数据Table 1 Naphtha oil property data

4.3 油品数据测试

在过去的很多文献中，通常根据反应机理判断和先验经验选择正构烷烃质量分数与异构烷烃质量分数作为影响乙烯收率原料的特征变量。在表2中FCM和EM_FCM[13]两行数据展示了选取石脑油中正构烷烃和异构烷烃的质量分数作为特征属性的聚类结果。

表2 聚类有效性指标Table 2 Cluster validity index

本文利用随机森林方法对石脑油油品特征进行特征选择，展示不同特征属性对乙烯收率的贡献度。如图3所示，纵坐标为石脑油特征属性对乙烯收率的贡献度，从图中可以看出正构烷烃质量分数、10%镏点、密度、初馏点、30%镏点的贡献度要大于其余属性，经实验验证，选取前4种特征属性取得较好的效果，如表3所示。特征属性的贡献度为正值表明对目标值具有很强的正面影响，负值代表特征属性对目标为负面影响。

在表2中，聚类类别数C=4，对数据迭代50次取均值得到最后的Dunn评价指标。可以看出本文选择影响乙烯收率的主要特征属性：正构烷烃质量分数，10%镏点，密度，初馏点作为石脑油的特征属性进行聚类，结果如图4所示，要明显高于文献[13]中所提出的利用EM_FCM算法选择正构烷烃质量分数和异构烷烃质量分数作为主要特征属性的结果如表2所示。本文结果相较于文献[13]的聚类效果更好是因为在代入算法前，利用随机森林算法对石脑油的特征属性进行特征选择，选择那些对乙烯产率贡献度大的特征作为石脑油代入聚类算法的特征，同时IKFC算法中引入直觉模糊集理论定义犹豫度及其熵，使其相比较FCM、EM_FCM和MKFC算法更善于处理数据集中不确定信息，如图5所示。

图3 特征属性的贡献度Fig.3 Contribution degree of attribute

表3 前4种与5种特征属性聚类结果对比Table 3 Comparison of four kinds with five kinds of attributes

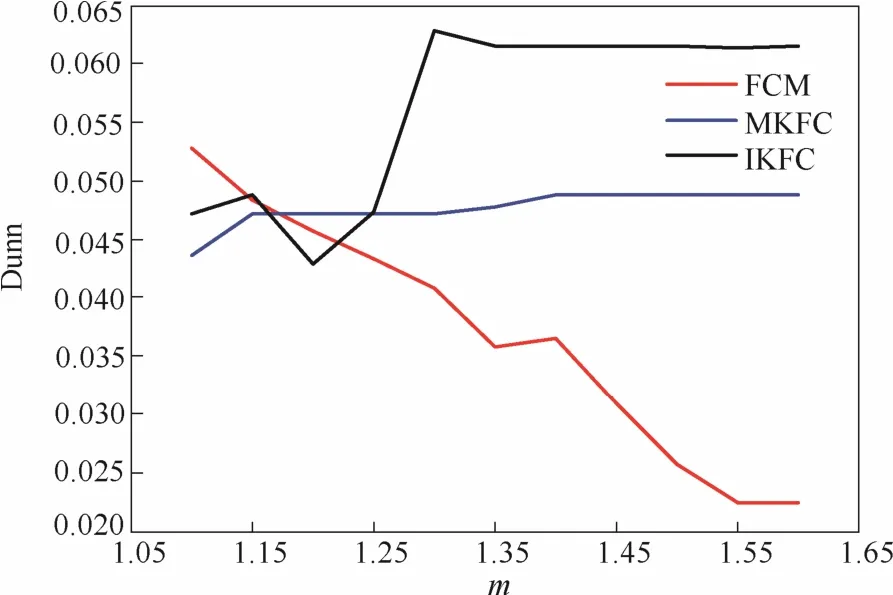
图4 石脑油Dunn数据指标对比Fig.4 Comparison of naphtha oil index

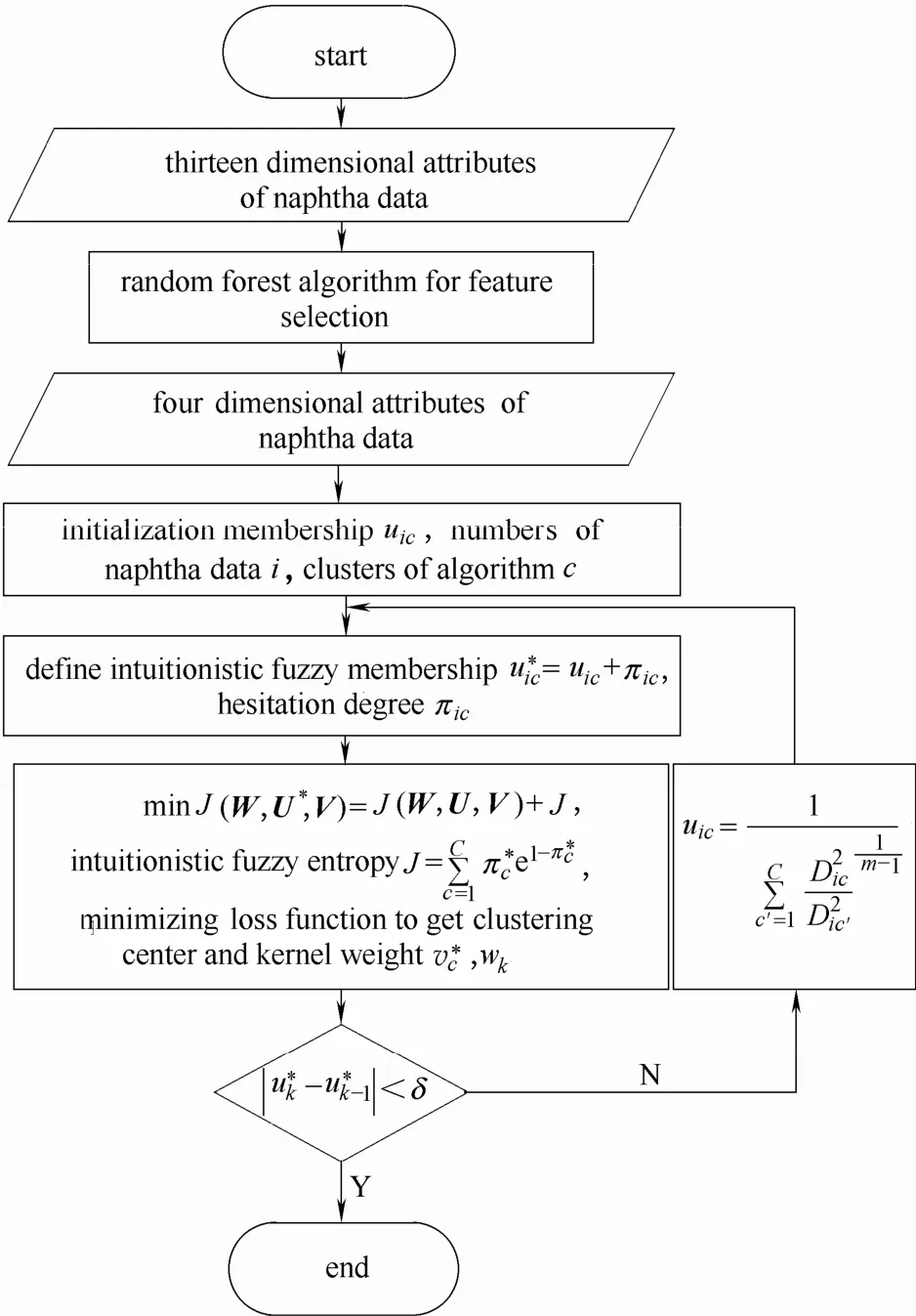
图5 随机森林和直觉模糊多核聚类算法流程Fig.5 Flowchart of random forest and IKFC algorithm

IKFC算法通过提高乙烯裂解原料属性的聚类精度，能够更加准确的确定模型数量，提高模型精度，从而能有效地指导原料-产率多模型的建立。

5 结 论

本文基于直觉模糊集理论，将犹豫度和直觉模糊熵引入到多核聚类算法上，解决了由于缺少先验知识致使隶属度定义不准确的问题。并利用随机森林算法进行特征选择，表示出石脑油不同属性对乙烯产率的贡献度。最后用石脑油数据进行仿真，验证了IKFC算法的精确性。然而该算法对隶属度的加权指数m的选择依赖性较大，如何确定m将是以后研究的重点。

[1] SONG G, TONG Q, CHEN B. Improved resource-task network-based flare minimization model for ethylene plant start-up: rigorous treatment of cracking furnace and high-pressure steam[J]. Industrial & Engineering Chemistry Research, 2015, 54(24): 6326-6333

[2] 彭辉, 张磊, 邱彤, 等. 乙烯裂解原料等效分子组成的预测方法[J].化工学报, 2011, 62(12): 3447-3451. PENG H, ZHANG L, QIU T,et al. Method of predicting equimolecular mixture of ethylene cracking feedstock[J]. CIESC Journal, 2011, 62(12): 3447-3451.

[3] 李平, 李奇安, 雷荣孝, 等. 乙烯裂解炉先进控制系统开发与应用[J]. 化工学报, 2011, 62(8): 2216-2220. LI P, LI Q A, LEI R X,et al.Advanced control system development and application of ethylene cracking furnance[J]. CIESC Journal, 2001, 62(8): 2216-2220.

[4] XU R, DONALD C W. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 645-678.

[5] MCLACHLAN G J, BEAN R W, PEEL D. A mixture model-based approach to the clustering of microarray expression data[J]. Bioinformatics, 2002, 18(3): 413-422.

[6] LUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416.

[7] KANNAN S R, DEVI R, RAMATHILAGAM S,et al.Effective FCM noise clustering algorithms in medical images[J]. Computers in Biology and Medicine, 2012, 43(2): 73-83.

[8] HAVENS T C, BEZDEK J C, LECKIE C,et al.Fuzzy c-means algorithms for very large data[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(6): 1130-1146.

[9] ZHANG D Q, CHEN S C. Clustering incomplete data using kernel-based fuzzy c-means algorithm[J]. Neural Processing Letters, 2003, 18(3): 155-162.

[10] HUANG H C, CHUANG Y Y, CHEN C S. Multiple kernel fuzzy clustering [J]. IEEE Transactions on Fuzzy Systems, 2012, 20(1): 120-134.

[11] ZHANG L, HU X. Locally adaptive multiple kernel clustering[J]. Neurocomputing, 2014, 137(11): 192-197.

[12] CORMA A, MENGUAL J, MIGUEL P J. Im-5 zeolite for steam catalytic cracking of naphtha to produce propene and ethene. An alternative to zsm-5 zeolite[J]. Applied Catalysis A: General, 2013, 460(11): 106-115.

[13] 李嘉雯, 杜文莉, 李进龙, 等. 基于改进模糊C均值聚类算法的乙烯裂解原料识别[J]. 化工学报, 2013, 64(12): 4366-4372. LI J W, DU W L, LI J L,et al. Feed property identification of ethylene cracking based on improved fuzzy c-mean clustering algorithm[J]. CIESC Journal, 2013, 64(12): 4366-4372.

[14] 陈贵华, 王昕, 王振雷, 等. 基于模糊核聚类的乙烯裂解深度DE-LSSVM多模型建模[J]. 化工学报, 2012, 63(6): 1790-1796. CHEN G H, WANG X, WANG Z L,et al. Multiple DE-LSSVM modeling of ethylene cracking severity based on fuzzy kernel clustering[J]. CIESC Journal, 2012, 63(6): 1790-1796.

[15] GENG Z Q, ZHU Q X. Dynamic kernel clustering algorithm and its application in optimal pattern recognition of ethylene production[J]. Control and Instruments in Chemical Industry, 2005, 32(2): 5-8

[16] CHAIRA T. A novel intuitionistic fuzzy c means clustering algorithm and its application to medical images[J]. Applied Soft Computing, 2011, 11(2): 1711-1717.

[17] LAKSHMANA G N V, SIVARAMAN G. Ranking of interval-valued intuitionistic fuzzy sets[J]. Applied Soft Computing, 2011, 11(4): 3368-3372.

[18] CHAIRA T, RAY A K. A new measure using intuitionistic fuzzy set theory and its application to edge detection[J]. Applied Soft Computing, 2008, 8(2): 919-927.

[19] LAKSHMANA G N V, SIVARAMAN G. Ranking of interval-valued intuitionistic fuzzy sets[J]. Applied Soft Computing, 2011, 11(4): 3368-3372.

[20] CHEN L, CHEN C L P, LU M. A multiple-kernel fuzzy c-means algorithm for image segmentation[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics, 2011, 41(5): 1263-74.

[21] WEI Z Z, FENG P. Analysis of rainfall-runoff evolution characteristics in the Luanhe River basin based on variable fuzzy set theory[J]. Journal of Hydraulic Engineering, 2011, 42(9): 1051-1057.

[22] XU Z, CHEN J, WU J. Clustering algorithm for intuitionistic fuzzy sets[J]. Information Sciences, 2008, 178(19): 3375-3790.

[23] PAL N R, PAL S K. Entropy: a new definition and its applications[J]. IEEE Transactions on Systems Man & Cybernetics, 1991, 21(5): 1260-1270.

[24] YAGER R R. On the measure of fuzziness and negation(Ⅰ): Membership in the unit interval[J]. International Journal of General Systems, 1979, 5(4): 221-229.

[25] CHAIRA T. A rank ordered filter for medical image edge enhancement and detection using intuitionistic fuzzy set[J]. Applied Soft Computing, 2012, 12(4): 1259-1266.

[26] BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32.

[27] BELMONTE M, YURGELUNTODD D. Permutation testing made practical for functional magnetic resonance image analysis[J]. IEEE Transactions on Medical Imaging, 2001, 20(3): 243-8.

[28] LUNA-ROMERA J M, GARCÍA-GUTIÉRREZ J, RIQUELME- SANTOS J C. An approach to silhouette and dunn clustering indices applied to big data in spark[M]//Advances in Artificial Intelligence. Berlin: Springer, 2016: 160-169.

[29] KOTSIANTIS S B, PINTELAS P E. Logitboost of simple Bayesian classifier[J]. Informatica, 2010, 29(1): 53-59.

[30] CHARYTANOWICZ M, NIEWCZAS J, KULCZYCKI P,et al.Complete gradient clustering algorithm for features analysis of X-ray images[M]//Information Technologies in Biomedicine. Berlin: Springer, 2010: 15-24.

Intuitionistic set theory based multiple kernel fuzzy clustering and its application of ethylene raw material properties

CUI Xinghua1, DU Wenli1, ZHAO Liang1, LI Jiangli2, CHI Liang2
(1State Key Laboratory of Chemical Engineering,Key Laboratory of Advanced Control and Optimization for Chemical Processes,East China University of Science and Technology,Shanghai200237,China;2PetroChina Jilin Petrochemical Company,Jilin132000,Jilin,China)

Along with the increasing types of ethylene cracking materials and expensive feed analyzer, clustering of ethylene cracking materials which is to improve ethylene yield modeling, ethylene yield and energy consumption has very important practical significance. In order to improve the accuracy of online identification of raw materials, an intuitionistic fuzzy kernel clustering algorithm based on the theory of intuitionistic fuzzy sets is presented. In the definition of membership, membership considers uncertain information which is the hesitation degree. At the same time, intuitionistic fuzzy entropy is incorporated in the loss function of multiple kernel clustering algorithm. That is to optimize the data points in the class. Further, the cracking material attribute feature selection using random forest, based on the main attributes of contribution of ethylene yield. Finally, the actual ethylene cracking naphtha data of industry is used to verify the effectiveness and superiority of the algorithm.

algorithm; entropy; optimization; intuitionistic fuzzy; ethylene cracking

Prof. DU Wenli, wldu@ecust.edu.cn

TP 227

：A

：0438—1157（2017）02—0739—07

10.11949/j.issn.0438-1157.20161069

2016-07-28收到初稿，2016-10-08收到修改稿。

联系人：杜文莉。

：崔兴华（1989—），男，硕士研究生。

国家自然科学基金重点项目（61590923）；国家自然科学基金优秀青年基金项目；国家自然科学基金青年科学基金项目（61422303，61403141）；上海市教育委员会和上海市教育发展基金会“曙光计划”资助项目。

Received date: 2016-07-28.

Foundation item: supported by the Key Program of National Natural Science Foundation of China (61590923), the National Science Fund for Excellent Young Scholars, the Young Scientists Fund of the National Natural Science Foundation of China (61422303, 61403141) and the Shanghai Municipal Education Commission and Shanghai Education Development Foundation “Dawn Project”.