石油供应链计划层优化与不确定性风险管理模型

赵用明，罗祎青，袁希钢

（化学工程联合国家重点实验室，天津大学化工学院，天津化学化工协同创新中心，天津 300072）

石油供应链计划层优化与不确定性风险管理模型

赵用明，罗祎青，袁希钢

（化学工程联合国家重点实验室，天津大学化工学院，天津化学化工协同创新中心，天津 300072）

提出了一种基于有限场景的两阶段随机混合整数线性规划(MILP)模型，来优化不确定条件下多周期、多层级的石油工业供应链的计划层管理。模型以碳排放税的形式将减少CO2排放的环境目标融入到经济目标之中。供应链的各级节点均以黑箱的形式存在，使模型得以简化，在时间尺度相对较长的计划层获得优化结果，为供应链的计划与管理提供指导方案。并且分析了算例最优期望收益的风险性，在此基础上引入风险管理约束，得到了带有风险管理约束的供应链计划层优化模型。该模型的结果与原模型相比，期望收益附近的收益风险性降低。

石油供应链；优化；不确定性；风险管理；系统工程

引 言

在经济全球化与信息技术快速发展的今天，企业的传统管理模式逐渐无法满足商业竞争的需要，供应链管理的概念日益受到关注[1]。与传统管理模式相比，供应链管理从系统的角度出发，协调与整合上下游各级企业，实现了全局利益的最大化。一般情况下，可以将其描述为从原材料的获取到产品输送到终端客户的全生命周期过程，涉及原材料供应商、产品制造商、分销商、零售商以及终端消费者等多个层级，是集成资源与生产的复杂网络。目前，供应链的相关研究受到广泛关注，Nickel等[1-4]对其进行过相关综述。

石油工业是国民经济的基础，具有投资大、能耗高、生产过程复杂等特点，从供应链的角度，合理地做出最优的各项决策对于企业的经济效益，乃至节能减排的环境效益都具有重大意义。按照决策的时间尺度，供应链的研究可以分为3个层次：战略层、计划层以及操作层[5]。本文关注的是石油工业供应链的计划层优化问题。

该层次的研究一般采用数学规划的方法，选择适当的优化目标进行最优化计算，可以得到最优的采购方案、生产方案、运输方案、库存方案以及销售方案等。Neiro等[6]提出了一种石油工业供应链建模的一般框架，以混和整数非线性规划(MINLP)模型来处理供应链的计划决策问题，模型细化了炼油厂的部分，为之后的石油工业供应链建模提供了范本。Chang等[7]将供应链模型的炼油厂部分更加细化，明确规定了炼油厂内部的单元与结构，并将模型简化为混合整数线线性规划(MILP)模型，在满足可靠性的基础上，缩短了优化时间。

在供应链进行优化管理时，由于信息无法完全掌握，会存在不确定情况，如原料的价格、产品的价格以及产品的需求等。Chen等[8]就以炼油厂为研究对象，以原油价格波动作为不确定情况，优化了采购方案。目前，针对石油工业供应链存在不确定情况的问题，主要有以下4种处理方法：随机规划[9]、机会约束规划[10]、鲁棒优化[11]以及模糊规划[12]。其中，基于有限场景的随机规划，可以依据经验，以概率的形式表示不确定性，是不确定条件下石油工业供应链优化的常用方法。

在使用该方法处理不确定情况的时候，可以采用风险管理技术[13]对优化目标的风险性进行管理，在获得最优目标的同时降低其风险性。Gebreslassie等[14]、Bagajewic等[15]以及Hamacher等[16]采用下游风险理论、风险价值理论(VaR)以及条件风险价值理论(CVaR)等对石油工业供应链的战略层等优化问题进行了风险管理研究。

在文献[7,11,17-18]中，在进行计划层的优化时，通常也会把操作层的部分结构，即各个节点内部的情况（尤其是炼厂内的部分内容）考虑在内。这种混淆计划层和操作层区别的建模思路虽然理论上可以获得更加实际可行的结果，但由于计划层和操作层所考虑的时间尺度上的差距，以及操作层在较小时间尺度上存在不确定性这一显著特征，必然会导致计划层的优化结果可行性的降低。因此原本复杂的建模思路其实并不能提高结果的可行性，是不需要的。本文放弃了现有的这种建模思路，在避免模型的复杂性的同时保持了其可行性，同时有助于供应链计划层和操作层的概念区分。本文的模型将石油工业供应链的各级节点假设为黑箱的形式，输入与输出的关系可以依据具体工业收集的数据来确定。在目标函数中以碳排放税的形式将减少二氧化碳排放的环境目标与企业的经济目标相结合，以提高环境质量的绿色红利与改善经济效率的蓝色红利[19]。这种形式可以依据相关部门对于碳排放量的限制程度而设定不同的税率，同时也符合企业的经济利益优先的思考角度，通过权衡经济收益和碳排放的经济惩罚做出最符合企业经济利益的计划方案。在处理不确定性时采用的是基于有限场景的随机规划方法，并且加入风险管理分析。最终得到了考虑风险性的石油工业供应链计划层优化模型，对于石油企业制定时间尺度相对较长的计划层管理方案具有一定的指导意义。

1 问题描述

图1为所研究的石油工业供应链模型的超结构，空间上是供应链的中游和下游的整合，包括原材料供应商、产品制造商、分销商、终端消费者4个层级，不涉及供应商原料获取的上游内容。其中原材料供应由本地油田(of1)和进出口码头(te1)两个部分组成，进出口码头内可包含多个不同的供应商。产品制造由3个操作模式不同的炼油厂(r1/r2/r3)组成，分销由3个分销中心(b1/b2/b3)和进出口码头完成，终端消费者包括两个海外消费者(oc1/oc2)和5个国内消费者(c1/c2/c3/c4/c5)。图中各个层级的节点数量可以根据情况进行增减。整体过程可以描述为原油等原料从码头或本地油田运输到炼油厂、炼油厂生产各种石化产品、产品输送到分销中心和进出口码头再分别输送给国内客户和海外客户。此外，模型允许为满足消费者订单而从外购买产品的情况发生，这一过程通过从进出口码头进口产品输送到分销中心和就地输送给海外消费者来实现。

在进行石油工业供应链计划层的优化时，目的是在满足客户订单的基础上，尽量提高整体的经济效益，并将降低碳排放量的环境目标融入其中。在完成优化之后，可以得到最优目标下的原油采购计划、炼厂生产计划、产品分销计划、节点间的运输计划以及仓储计划。由于供应链的结构已经固定，所以在进行优化时有些内容是确定的，如下：

图1 石油工业供应链超结构Fig.1 Schema of petroleum supply chain superstructure

（1）供应链的物理结构，如原料供应商、炼油厂、分销中心、固定客户的数量，位置以及各自之间的连接关系；

（2）供应链的内部信息，如原料的种类、性质，供应商可以提供的原料量上限，炼油厂的操作模式及其碳排放系数，生产的产品种类、性质以及产品在炼厂中的总体收率，炼油厂原料处理能力的上下限，炼油厂的原料库存量上限，分销中心和进出口码头的产品库存量上限，为补足订单可以购买的产品量上限，各个节点间的运输方式以及各种方式的运输量上限，生产过剩和订单不满足情况的产品量上限；

（3）供应链的成本系数，如炼油厂的操作费用单价，库存费用单价，运输费用单价，碳排放税率，生产过剩和订单不满足的惩罚费用单价。

而供应链的外部信息，如在计划层优化时需考虑的原料的价格、产品的价格、产品的需求以及为补足订单而购买的产品的价格不是供应链自身固有的信息，这些信息是存在不确定性的。在石油工业供应链计划层的研究中，制定计划前通常是可以得到供应商的原料报价的，所以在此假设原料的价格是确定的，而可能存在的不确定情况为产品的价格与需求。

除了假设原料的价格确定以外，为简化模型还需做出其他假设：

（1）在进行计划层的优化管理时，各时间周期内供应链的结构和内部信息是固定的，即不存在中途改造供应链的情况；

（2）包括炼油厂在内的各个节点都以黑箱的形式存在，进出口关系是可以通过数据分析获取的；

（3）原料的库存集中在炼厂内而产品的库存集中在分销中心和进出口码头内；

（4）存在不确定情况的部分，其可能的情况和发生概率是可以预测的；

（5）各种产品价格与需求的不确定情况变化是一致的，为补足订单而购买的产品价格因运费等原因比销售价格高，但不确定性的分布情况与其一致。

对于产品价格和需求的不确定情况采用基于有限场景的随机规划方法进行处理，将各种不确定情况的发生概率设为定值，并对两种不确定情况进行耦合得到如图2所示的不确定场景分布情况。

图2 不确定情况的场景及概率分布Fig.2 Scenariotree with probability under uncertainties of product price and demand(Pi,Pj,Psare probability of different condition of product price, demand and integration of them respectively)

2 数学模型

为解决上述石油工业供应链的计划层优化问题，建立了一个基于有限场景的两阶段随机规划模型。其一般形式[20]可表述为

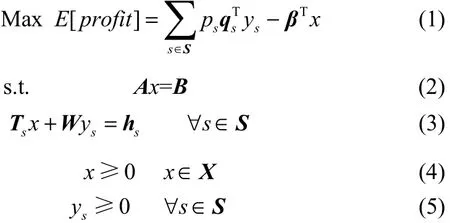
其中，x代表第1阶段决策变量，ys代表与场景s有关的第2阶段决策变量，而场景s的发生概率由ps来表示，目标函数是第2阶段收益减去第1阶段成本的净收益最大化。β、A、B、W为确定性的参数，qs、Ts、hs为与场景有关的不确定参数。

2.1 石油工业供应链计划层优化的目标函数

建立的两阶段随机规划模型的目标函数为期望经济收益的最大化，具体是指产品销售的收益Profits减去供应链整体运行成本的期望值，成本的内容包括原料采购费用Cmp，为补足订单额外购买产品费用Cpps，炼油厂的操作费用Cros，原料运输费用Cmtr，产品运输费用Cptrs，库存费用Cins，碳排放税Cctaxs，生产过剩惩罚费用Csurs，未满足订单惩罚费用Cbcks。其中只有原料购买费用和原料运输费用与不确定的场景无关，为目标函数的第1阶段部分，其余组成与场景有关的第2阶段部分。具体的数学形式表达如下

在此，以碳排放税的形式将石油工业供应链运行的环境影响中CO2的排放量考虑到了目标函数当中，式中的TAXC为单位CO2排放的税率，其具体数值目前尚有争论。在我国，一般建议为10 CNY·t-1或20 CNY·t-1。ECr表示的是不同结构和操作的炼油厂的CO2排放系数，即单位原料处理量的CO2排放量，在工业实际中，其具体数值可以通过相关的计算方法[21]进行数据分析获得。在本文中，采用陈宏坤等[22]计算的碳排放系数近似地进行优化研究。若遇到CO2排放量有硬性约束的情况，可以考虑在目标函数中去除该部分，改为增加约束条件

生产过剩惩罚费用和未完成订单惩罚费用可以表示为

2.2 石油工业供应链计划层优化的约束条件

依据既定的石油工业供应链网络，其存在的约束条件可以分为以下几类：物料平衡约束；产品性质约束；采购、库存、运输以及生产的能力约束；生产过剩与订单不满足协调的需求约束。

2.2.1 物料平衡约束 物料平衡约束包括原料的物料平衡约束和产品的物料平衡约束以及进出各个节点的混合与分布约束。原料的物料平衡约束可表示为

在产品的物料平衡约束中，式(20)、式(21)、式(22)、式(23)分别以炼油厂、分销中心、进出口码头为核心。

各个节点的混合与分布约束可以表示为

2.2.2 产品性质约束 石油产品在性质上可能会有一些限制规定，如含硫量、含蜡量等。在此加入产品性质约束以满足相关规定。此约束会对不同性质的原料采购选择和不同操作模式的炼油厂选择产生影响。其数学形式表达如下

RRPRr,m表示炼油厂r对于原料m的某性质的改变比例，如对于硫的脱除比例。

2.2.3 能力约束 采购能力约束包括原料的采购量上限和为补足订单购买产品的采购量上限。表达如下

2.2.4 需求约束

对于同一种产品来说，生产过剩和订单未满足这两种情况是不能同时存在的，且这两种情况都应存在一定的限度，所以增加以下约束

2.3 带有风险管理约束的计划层优化模型

在进行石油工业供应链计划层优化时，目的是使期望收益最大化，当某种情况得到的收益比期望收益低时，就说明这种情况存在风险，因此可以采用风险管理技术对优化结果进行分析。风险管理经常与二阶段随机规划结合在一起进行研究。风险的定义如下

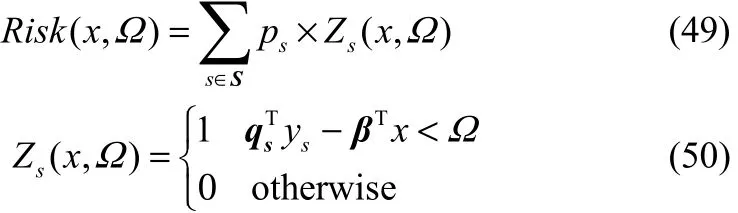
Us表示一个数值很大的正数，保证上述的式(52)和式(53)只有一个成立。对于多目标优化模型，可以采用引入权重系数的方法，将多目标转化为单目标形式，进行求解。式(51)的形式变为

ω为权重系数，是一个正数。

3 算例研究

采用文献[23]中的算例进行计算，具体内容进行了一定的调整和修改，算例的供应链结构与图1一致。原料包括本地油田(of1)提供的两种原油，进出口码头(te1)内包含3个供应商提供的6种原油和轻石脑油、重石脑油、混合二甲苯。3个炼厂的产品略有不同，具体产品及其总体收率如表1所示。选择的时间周期为1个月，共3个时间周期，为一个季度的计划优化。存在4种运输方式，进出口码头到海外客户为海运；码头、油田与炼油厂之间，炼油厂与分销中心之间以及码头与分销中心之间为管道和公路两种运输方式；分销中心与国内客户之间为公路和铁路两种运输方式。由于篇幅所限，其他已知参数不予列出。

表1 3个炼厂的产品及基于炼厂的整体收率Table 1 Products and yield ratio in three different refinery

3.1 不确定场景的确定

不确定场景及其概率分布基于文献[18]的讨论来确定。产品价格和需求各分为3种情况，耦合得到9种情况。预测的产品一般价格和需求的场景概率均设定为50%，并将低于一般情况20%的低水平情况和高于一般情况20%的高水平情况的发生概率都定为25%，最终场景及概率分布情况如图3所示。

图3 算例的不确定场景及概率分布Fig. 3 Scenariotree with probability under uncertainties of case

3.2 结果分析与讨论

将算例的已知参数以及不带风险管理约束的计划层优化模型输入到GAMS软件中进行优化。模型为混合整数线性规划(MILP)，选择CPLEX求解器进行优化求解。模型计算参数如表2所示。优化目标是期望收益的最大化，优化得到的最优期望收益以及场景平均的各项成本花费如表3所示。成本的组成分析如图4所示。从图中可以看出，在该供应链计划层管理的各项成本中原料的采购成本占比最大，超过了一半，其次为炼油厂的操作费用，生产过剩的惩罚、库存费用以及碳排放税相对占比较低。各种成本的占比情况与算例的已知参数有关，更改参数会导致成本的占比发生变化。除此之外还可以得到最优期望收益下供应链计划层的各种决策方案，具体如表4所列，在此只把原料采购方案的数据列出，如表5所示。

表2 GAMS模型参数统计Table 2 GAMS model statistics

表3 最优期望收益和相应的成本花费Table 3 Optimal expected profit and cost/ USD

由于存在不确定场景，所以在得到最优期望收益的同时也会得到9个不同场景下的收益，结果如表6所示。收益的相对高低与对应的场景在经验上的判断是一致的。依据表6所示的不同概率情况下的收益，可以根据风险的定义绘制风险曲线如图5所示。图中的横坐标为不同的目标收益Ω，纵坐标为该目标收益下的风险。虚线表示的是该两阶段随机规划计算的最优期望收益5.439×107USD，与风险曲线的交点对应的纵坐标为该期望收益的风险，约为37.8%，即在上述不确定场景分布的情况下，有37.8%的可能性获得的收益低于优化得到的期望收益。如果将优化目标改为不存在不确定性的一般情况，即场景5的收益，计算结果是在优化目标中不考虑产品价格和需求存在不确定性而得到的，该结果可以重新绘出一条风险曲线，两种情况的对比如图6所示。可以看出，考虑不确定情况的随机优化模型得到的收益要比不考虑优化目标存在不确定情况的模型在风险性上具有较大的优势，有利于决策者做出较低风险的计划层决策。

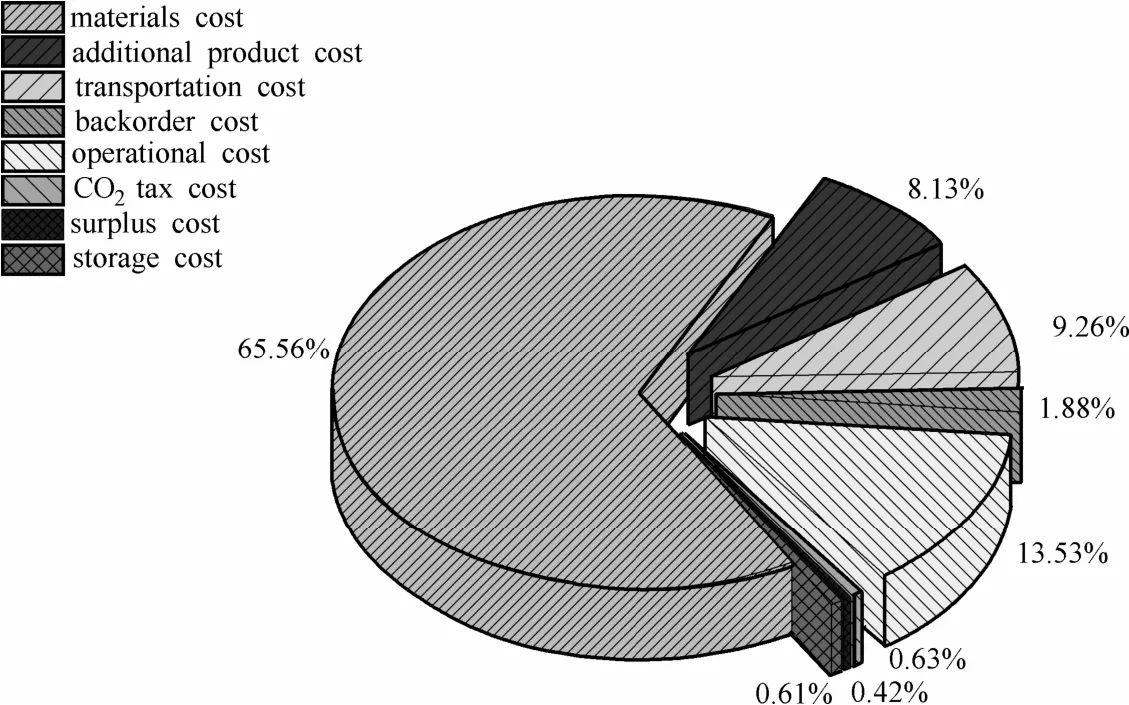
图4 最优期望收益下的成本分析Fig. 4 Cost analysis of optimal expected profit

表4 优化后可以得到的决策方案Table 4 Decision scheme of optimal objective

表5 最优期望收益下的原料采购计划方案Table 5 Scheme of raw material purchasing of optimal expected profit

表6 9种不确定场景下的收益及其发生概率Table 6 Profit of nine scenarios with different probabilities

图5 最优期望收益的风险曲线Fig.5 Risk curve of optimal expected profit

图6 不同优化目标的风险曲线对比Fig.6 Comparison of risk curve with different objective

虽然随机规划模型的风险性比确定性的低很多，但得到的最优期望收益仍然存在37.8%的风险。为此，在优化模型中增加风险管理约束，使优化目标在最大化期望收益的同时降低目标收益的风险。模型如2.3节所示，风险在优化目标中的权重尽量选大一点，选择增加到约束中的目标收益为最优期望收益附近的5.5×107、5.6×107、5.7×107USD，结果的风险曲线如图7所示。可以看出，在优化模型中增加风险管理约束，会降低目标收益附近区域收益的风险。而相对应的计划决策方案也发生了变化，不增加风险约束的模型和目标收益定为5.7×107USD的带有风险管理约束约束的模型的优化原料采购方案的对比如表7所示。

（4）采取增强安全措施：可将OPC服务器隔离到只包含授权设备的唯一分区中，并采用“分区加固、身份认证”技术，达到纵深防御的目的。

图7 加入不同目标收益风险管理约束后的风险曲线Fig.7 Risk curve of adding risk constraints with different target profit [(b) is partial enlarged view of (a)]

4 结 论

（1）本文提出了一种基于有限场景的两阶段混合整数线性随机规划模型来对石油工业供应链的计划层进行决策优化。模型将其中的节点以黑箱的形式处理，在时间尺度相对较长的计划层研究中，简化了供应链操作层面的复杂结构，使决策者可以较为简便地对中长期的计划进行决策判断。在模型的优化目标函数中，以碳排放税的形式将减碳的环境目标与原本的经济目标进行了结合。对模型进行了算例分析，选择的不确定场景耦合了产品价格低中高3种情况与产品需求低中高3种情况，共生成了9种不同的场景。并对模型得出的优化结果进行了风险性分析，通过对比发现考虑不确定性的随机规划较确定性模型整体风险性更低。之后在随机规划模型中加入了风险管理约束，计算结果表明加入风险管理约束后的优化模型的优化结果在目标收益附近的风险有所降低。提出的模型对于石油工业供应链的计划层优化管理具有一定的指导意义。

（2）本文只研究了石油工业供应链计划层的优化问题，做出的是时间尺度相对较长的计划层优化方案。但是由于信息的偏差与操作层可能存在的不确定情况，计划层的方案可能会在操作层次上无法完全实现。因此，考虑在之后的研究中把操作层的优化与本文中的计划层优化进行集成，得到计划层与操作层的集成优化模型，得出更加准确可行的计划层管理方案和操作层的调度方案。

表7 有无风险管理约束的最优原料采购计划方案对比Table 7 Comparison of scheme for raw material purchasing between original model and model with risk management

符 号 说 明

A——第一阶段约束确定性参数矩阵

B——第一阶段约束确定独立向量

BCK——未满足订单的单位惩罚费用

BDQ——未满足订单的上限

bdq——未满足订单的量

Cbck——未满足订单惩罚费用

Cctax——碳排放税费用

Cin——库存成本费用

Cmp——原料采购成本费用

Cmtr——原料运输成本费用

Cpp——产品采购成本费用

Cptr——产品运输成本费用

Cro——炼油厂操作成本费用

Csur——生产过剩惩罚费用

DEM——需求量

DIS——任意两节点间的距离

E——期望收益

EC——炼油厂的二氧化碳排放系数

h——第二阶段约束独立随机向量

ibdq——0-1变量，表示生产不足情况是否存在

isdq——0-1变量，表示生产过剩情况是否存在

MCC——原料价格

mf——任意两节点间的原料运输量

MOFU——本地油田的采购量上限

MTEU——进出口码头的采购量上限

OCA——炼油厂处理原料的单位操作费用

p——概率

pf——任意两节点间的产品运输量

pfbi——进口的产品输送到分销中心的量

pfro——炼油厂的产品输出量

pfrob——炼油厂输送到分销中心的产品量

pfrote——炼油厂输送到进出口码头的产品量

pftei——从进出口码头进口的产品量

PP——进口的产品价格

PR——物料的性质

Profit——销售收益

PTEU——额外产品的采购量上限

q——递归矩阵的随即参数

qmf——原料采购计划量

qout——分销到客户的产品实际到货量

qrmf——炼油厂实际处理的原料的量

RRPR——性质的改变比例

SDQ——生产过剩的上限

sdq——生产过剩的产品量

SP——产品价格

SUR——生产过剩的单位惩罚费用

T——第二阶段约束矩阵

TAXZC——单位二氧化碳排放的税率

TC——单位距离单位物料的运输费用

TCAU——运输量上限

TCO2——二氧化碳排放量硬性要求上限

U——一个极大数

VC——库存单价

vm——原料库存量

VMU——原料库存量上限

vp——产品库存量

VPU——产品库存量上限

W——确定性递归矩阵

x——第一阶段决策变量

y——第二阶段决策变量

YDR——整体收率

Z——0-1变量，表示小于目标收益的情况是否存在

β——第1阶段约束确定参数变量

ω——风险在优化目标里的权重

Ω——目标收益

下角标

b——分销中心

c——国内客户

i——产品价格场景

j——产品需求场景

m——原料

oc——海外客户

of——本地油田

p——产品

r——炼油厂

te——进出口码头

tp——时间周期

s——不确定场景

上角标

s——不确定场景

T——转置符号

[1] SAHEBI H, NICKEL S, ASHAYERI J. Strategic and tactical mathematical programming models within the crude oil supply chain context—a review[J]. Computers & Chemical Engineering, 2014, 68: 56-77.

[2] BARBOSA-PÓVOA A P. Process supply chains management—where are we? where to go next? [J]. Frontiers in Energy Research, 2014, 2: 23.

[3] PAPAGEORGIOU L G. Supply chain optimization for the process industries: advances and opportunities[J]. Computers & Chemical Engineering, 2009, 33(12): 1931-1938.

[4] GARCIA D J, YOU F. Supply chain design and optimization: challenges and opportunities[J]. Computers & Chemical Engineering, 2015, 81: 153-170.

[5] SHAH N. Process industry supply chains: advances and challenges[J]. Computers & Chemical Engineering, 2005, 29(6): 1225-1235.

[6] NEIRO S M S, PINTO J M. A general modeling framework for the operational planning of petroleum supply chains[J]. Computers & Chemical Engineering, 2004, 28(6/7): 871-896.

[7] KUO T H, CHANG C T. Optimal planning strategy for the supply chains of light aromatic compounds in petrochemical industries[J]. Computers & Chemical Engineering, 2008, 32(6): 1147-1166.

[8] CHEN R, DENG T, HUANG S,et al. Optimal crude oil procurement under fluctuating price in an oil refinery[J]. European Journal of Operational Research, 2015, 245(2): 438-445.

[9] AL-OTHMAN W B E, LABABIDI H M S, ALATIQI I M,et al. Supply chain optimization of petroleum organization under uncertainty in market demands and prices[J]. European Journal of Operational Research, 2008, 189(3): 822-840.

[10] YOU F, GROSSMANN I E. Design of responsive supply chains under demand uncertainty[J]. Computers & Chemical Engineering, 2008, 32(12): 3090-3111.

[11] LUO C P, RONG G. A strategy for the integration of production planning and scheduling in refineries under uncertainty[J]. Chinese Journal of Chemical Engineering, 2009, 6(1): 113-127.

[12] 王继帅, 荣冈, 冯毅萍. 不确定条件下石化企业供应链计划优化[J]. 化工学报, 2011, 62(8): 2157-2163. WANG J S, RONG G, FENG Y P, Optimization for petrochemical supply chain planning under uncertainty[J]. CIESC Journal, 2011, 62(8): 2157-2163.

[13] ANDRES B, BAGAJEWICZ M J. Managing financial risk in planning under uncertainty[J]. AIChE Journal, 2004, 50(5): 963-989.

[14] GEBRESLASSIE B H, YAO Y, YOU F. Design under uncertainty of hydrocarbon biorefinery supply chains: multiobjective stochastic programming models, decomposition algorithm, and a comparison between CVaR and downside risk[J]. AIChE Journal, 2012, 58(7): 2155-2179.

[15] LAKKHANAWAT H, BAGAJEWICZ M J. Financial risk management with product pricing in the planning of refinery operations[J]. Industrial & Engineering Chemistry Research, 2008, 47(17): 6622-6639.

[16] CARNEIRO M C, RIBAS G P, HAMACHER S. Risk management in the oil supply chain: a CVaR approach[J]. Industrial & Engineering Chemistry Research, 2010, 49(7): 3286-3294.

[17] ROCHA R, GROSSMANN I E, ARAGÃO M V S P D. Petroleum allocation at PETROBRAS: mathematical model and a solution algorithm[J]. Computers & Chemical Engineering, 2009, 33(12): 2123-2133.

[18] LEIRAS A, RIBAS G, HAMACHER S,et al. Tactical and operational planning of multirefinery networks under uncertainty: an iterative integration approach[J]. Industrial & Engineering Chemistry Research, 2013, 52(25): 19-26.

[19] 吴建军, 吴永刚, 常娟. 碳税和碳交易的应用现状分析[J]. 能源技术经济, 2012, 24(1): 10-13. WU J J, WU Y G, CHANG J. Study on current application of carbon tax and carbon trading [J]. Energy Technology and Economics, 2012, 24(1): 10-13.

[20] BIRGE J R, LOUVEAUX F. Introduction to Stochastic Programming[M]. Springer Science & Business Media, 2011: 182.

[21] 蒋庆哲, 马敬昆, 陈高松, 等. 炼油厂二氧化碳排放估算与分析[J].现代化工, 2013, 33(4): 1-4. JIANG Q Z, MA J K, CHEN G S,et al. Estimation and analysis of carbon dioxide emissions in refineries[J]. Modern Chemical Industry, 2013, 33(4): 1-4.

[22] 陈宏坤, 田贺永, 肖远牲,等. 我国炼油行业碳排放估算与分析[J].油气田环境保护, 2012, 22(6): 1-3. CHEN H K, TIAN H Y, XIAO Y S,et al. The Estimation and analysis of carbon emission in the oil refining industry of China[J]. Environmental Production of Oil & Gas Fields, 2012, 22(6): 1-3.

[23] AND T H K, CHANG C T. Application of a mathematic programming model for integrated planning and scheduling of petroleum supply networks[J]. Industrial & Engineering Chemistry Research, 2008, 47(6): 1935-1954.

An optimization model for tactical decision-making level and uncertainty risk management in petroleum supply chain

ZHAO Yongming, LUO Yiqing, YUAN Xigang
(State Key Laboratory of Chemical Engineering,Collaborative Innovation of Chemical Science and Engineering(Tianjin),School of Chemical Engineering and Technology,Tianjin University,Tianjin300072,China)

A finite-scenario-based two-stage stochastic mixed integer linear programming (MILP) model was proposed to optimize tactical decision-making level of multi-period and multi-echelon petroleum supply chains under uncertain circumstances. In the model, environmental objective of CO2emission reduction was added to economic objective by collecting carbon tax, and each entity in the supply chain was considered as a “black box”to simplify the complicated system. A relatively reliable optimal result was obtained from the model over a considerably long duration to facilitate plan and management of petroleum supply chain. Further, risks to achieve the optimal outcome were analyzed and the model was revised with risk management constraints. Compared to the original model, the proposed model with risk management constraints could lower risks for the expected profit.

petroleum supply chain; optimization; uncertainty; risk management; system engineering

Prof. YUAN Xigang, yuanxg@tju.edu.cn

TQ 021.8

：A

：0438—1157（2017）02—0746—13

10.11949/j.issn.0438-1157.20160909

2016-07-04收到初稿，2016-12-04收到修改稿。

联系人：袁希钢。

：赵用明（1991—），男，硕士研究生。

中国工程院重点咨询研究项目：天津滨海新区建设循环经济示范区的发展战略咨询研究（2014-XZ-9）。

Received date: 2016-07-04.

Foundation item: supported by the Key Consulting Research Program of Chinese Academy of Engineering: the Consulting Research of the Development Strategy of Constructing Circular Economy Demonstration area in Tianjin Binhai New Area (2014-XZ-9).