基于神经网络的系泊系统主动式截断试验仿真

张隆辉，魏纳新，匡晓峰，范亚丽

(中国船舶科学研究中心，江苏 无锡 214082)

基于神经网络的系泊系统主动式截断试验仿真

张隆辉，魏纳新，匡晓峰，范亚丽

(中国船舶科学研究中心，江苏 无锡 214082)

系泊系统主动式截断试验技术对缆索数值模型的求解速度有着较高的要求，而基于集中质量模型或有限元模型的缆索数值模型在计算时需要在每个时间步内迭代求解，因此求解速度缓慢；为解决此问题，采用神经网络辨识得到缆索上端点与截断点运动的时域等价近似模型；该等价模型在每个时间步内无需迭代求解，因此求解速度快于传统的缆索数值模型；同时利用商软OrcaFlex以及Matlab搭建了系泊系统主动式截断试验的仿真平台，将离线辨识得到的神经网络模型代替集中质量模型对缆索截断点运动进行求解；通过对比截断水深以及全水深下张力以及运动结果，说明了神经网络模型代替传统数值模型进行截断点运动计算的可行性。

主动式截断；神经网络；系泊系统；缆索动力学

0 引言

海洋平台的系泊及其立管系统模型试验是系泊/立管系统设计的重要组成部分。然而随着海洋平台的工作水深不断增大，目前现有的海洋工程试验水池的大小难以满足采用常规比尺的海洋平台及其系泊/立管模型的试验要求[1]。为解决海洋工程试验水池尺度小于模型尺度的问题，研究人员提出了两种解决问题的方法，即被动式模型截断试验方法与主动式模型截断试验方法[2]。其中被动式模型截断试验方法是目前所广泛采用的方法，但是该方法忽略了缆索的动力学特征，仅能实现截断水深与全水深系泊系统的静力等价相似，并且需要引入数值计算过程得到最后的试验预报结果，因此被认为是一种间接获取试验结果的试验手段[3]。

相比于被动式模型截断试验方法，主动式模型截断试验方法考虑了缆索的动力学特征，能够试验截断水深与全水深系泊系统的动力学相似，并且直接通过模型试验获得预报结果。主动式模型截断试验方法的基本原理如图1所示，被截断的系泊缆索与安放于水池底部的伺服机构相连，伺服机构则根据上位计算机所发出的控制指令执行运动。上位计算机中存储有可靠的缆索数值模型(如集中质量模型、有限元模型)，其计算边界条件通过传感器实时采集获得，并实时计算缆索截断点的运动信息，从而发出控制指令对伺服机构实施控制。

图1 主动式技术基本原理图

目前国内外的主动式模型截断试验技术仍处于初始研究阶段，国内高文军、洪文渊等人[4-5]针对系泊缆索的上端点与截断点的运动建立了相应的传递函数，从频域上探讨系泊缆索截断点处的动力响应的规律。国外Buchner等人[6]提出了发展主动式模型截断技术的初步计划；Yuson Cao等人[7]则在假设计算机计算能力足够的情况下，对正弦工况下的主动式模型截断试验进行仿真，通过使用PID算法对位移偏差进行修正，仿真结果良好。以上研究工作皆提到计算机的实时计算能力对主动式模型截断试验技术的重要性，这是因为如基于集中质量模型或有限元模型的缆索数值模型在每个时间步的计算中需采用牛顿迭代法求解其非线性约束方程，故甚为费时。本文中，通过采用神经网络对缆索截断点运动进行离线模型辨识得到缆索上端点与截断点传递关系的时域运动模型，并代替传统缆索数值模型进行在线缆索截断点运动计算。由于辨识得到的网络模型不需要采用牛顿迭代法进行在线迭代求解，因此较传统数值方法有更快的求解速度。

1 神经网络

神经网络具有良好的非线性映射能力、自学习适应能力和并行处理信息的能力，因此常用于未知不确定的非线性系统模型的辨识工作[8]。近年来神经网络亦被广泛地应用于解决海洋平台运动预报及其系泊系统张力预报的问题中，如R. Guarize等人[9]将神经网络应用于某FPSO的运动与系泊系统的张力预报，通过将有限元方法计算得到的FPSO运动时历作为训练数据代入创建的神经网络进行训练，再利用训练好的神经网络预报得到FPSO的运动以及系泊系统导缆孔处的张力时历。MA Uddin等人[10]则将Narx网络应用于SPAR平台运动及其系泊系统的张力预报中，同样也获得了良好的预报结果。神经网络在这些问题中的成功应用，说明了采用网络对缆索模型进行辨识的可行性。

1.1 NARX网络

采用MATLAB中的神经网络工具箱创建辨识所用的神经网络模型。网络的基本结构如图2所示，其中未知动态系统为基于集中质量模型的缆索动力学数值模型[11]，u为缆索上端点的位移输入，y为缆索截断点的位移输出，n为时间步，q为延迟阶数，则NARX网络的基本表达式可以表示为：

(1)

式中f(·)为神经网络模型所表示的非线性函数，此处采用两层神经网络结构，故其可以表示为：

(2)

其中(y(n),…,y(n-q+1),u(n),…,u(n-q+1))∈xl，φj为S形激活函数，Fi为线性函数，Wi,j以及wj,l为各层未知权系数值，可采用贝叶斯正则化误差反向传播算法确定[12]。由于网络的输入不仅包含了当前时刻的输入信息，也包含了过去时刻的输入、输出信息，因此又称该神经网络为NARX网络，即带有外部输入的非线性自回归神经网络。

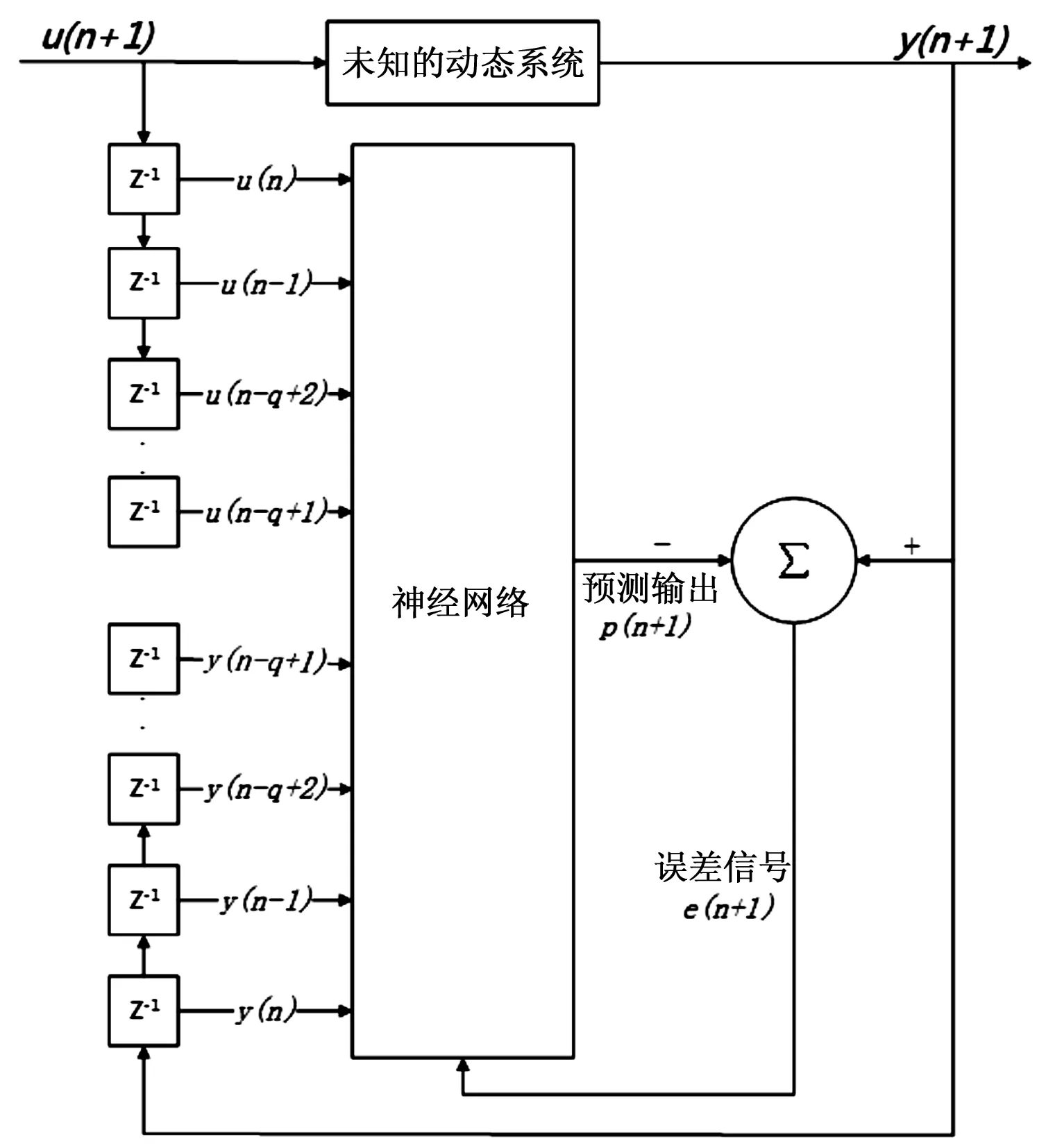
图2 NARX网络结构示意图

1.2 数据准备与网络训练

以工作于320米水深的半潜平台及其系泊系统为研究对象，其系泊系统布置图如图3所示，为四根多组分缆索呈近45°角对称布置。系泊系统缆索参数可见表1。

图3 系泊系统布置图

项目上端中间下端长度/m08742直径/m49×10-3355×10-349×10-3轴向刚度/N82402177558240线密度/(kg/m)011500660115

考虑试验水池的尺度，取缆长4米处对缆索进行截断。文中仅对图3中的4号缆索(Line4)进行截断分析，并设置3个工况如表2所示。其中工况1为训练工况，提供网络的训练数据；工况2、3为验证工况，用于验证网络在非训练工况下的推广性能，工况1～3所对应的海况依次减小。

表2 不同工况下海浪谱参数

在对NARX网络进行训练前需确定网络中的神经元数目以及延迟阶数，并选取适当的训练样本。通过试凑法选取网络的延迟阶数为40，并根据公式确定网络的神经元数目为15。对工况1总共计算了3 600秒时长缆索上端点以及截断点的运动数据，取其中的350秒为训练数据，150秒数据为训练验证数据。

(3)

其中：l为隐含层神经元数，m为输入层节点数，n为输出层节点数，a为1～10间的常数。

1.3 网络离线训练结果检验

工况1条件下的网络截断点位移离线计算结果如图4所示，由图4(a)～(c)的局部时历结果可以看到网络计算结果与集中质量法计算结果基本符合；由图4(d)～(f)的相关性分析结果可以看到X,Y,Z三个方向的位移相关性分析R值分别为0.999，0.999以及1，说明神经网络于截断点计算结果在整个3 600秒的时长内与集中质量法计算结果符合良好。因此可将离线训练得到的网络NET_0.12_2.15(其中0.12为波高，2.15为谱峰周期)用于主动式模型截断试验的在线仿真中。

图4 工况1截断点离线计算情况

2 主动式模型截断试验仿真

2.1 仿真平台基本原理

利用海洋平台及其系泊系统动力学分析软件OrcaFlex以及其所提供的外部Python函数接口，实现了OrcaFlex与Matlab两款软件之间数据传递，从而搭建主动式模型截断试验的在线仿真平台。仿真平台基本结构如图5所示，通过Python函数接口，每个时间步内Line4的上端点(即平台导缆孔处)位移信息实时传递到MATLAB中的NARX网络模型进行截断点的运动计算，再通过Python函数接口返回OrcaFlex中，对OrcaFlex中的虚拟机构实施位移控制。图6为OrcaFlex中的海洋平台及其系泊系统模型，其中左下的方块为OrcaFlex中的虚拟执行结构，其位置在每个计算时间步内都将根据神经网络的计算结果而实时更新。

图5 仿真平台基本工作流程

图6 OrcaFlex中平台及其系泊系统模型

2.2 主动式模型截断试验仿真结果与分析

将主动式混合模型试验仿真结果记为截断水深结果，全水深模型的耦合分析计算结果为全水深结果，截断水深以及全水深情况下的平台受到的波浪时历是一致的。

1)工况1结果：

图7 工况1 截断水深与全水深张力对比

工况1条件下的Line4相关时历结果可见图7，由图(a)、(b)上可以看到，缆索张力结果基本一致，但截断水深的结果的最值与全水深情况下差异较大，最大值以及最小值的相对误差分别为3.13%以及23.07%(张力的相关统计结果可见下表3)。同时由张力时历的局部放大图可以看到，截断水深张力的高频“毛刺”要较全水深情况下的更为明显；产生的原因则可能是由于截断点处的执行机构运动位移量由于无法完全与全水条件下缆索对应点处的位移量相同，因此截断点处的运动偏差所导致的缆索拉伸变形在一定程度上对缆索的张力造成了影响，故出现了较多“毛刺”。

表3 缆索Line4张力值统计结果(模型尺度)

缆索上端点(即导缆孔)处的运动统计结果如表4所述，截断水深以及全水深情况下3个方向上的位移量统计结果符合良好，其最大相对误差不超过8%，为7.53%，最小相对误差为0.01%。因此可以认为即使考虑平台与缆索之间的耦合，采用NARX网络进行截断点的计算对位移的统计值也不会造成太大的影响。

2)工况2、3结果：

验证工况2、3的张力计算结果如图8所示。可以看到，利用工况1数据离线训练得到NARX网络NET_0.12_2.15并将其应用于工况2中的截断点位移量计算，由此所得的Line4缆索张力与全水深情况下Line4张力亦基本一致；从图8(a),(b)可以看出工况2条件下的截断水深的缆索张力中也存在明显“毛刺”。另一方面，工况3条件下由于有义波高与谱峰周期与工况1条件相差较大，NARX网络性能下降明显，故相应的可由图8(c),(d)中可以看到截断水深缆索张力较全水深缆索张力差异很大。

工况2、3条件下的Line4上端点位移统计结果如表6所示。工况2条件下位移量最大相对误差4.73%，最小相对误差为0.09%，因此可以认为截断水深位移结果与全水深位移结果符合良好。但工况3条件下的Line4上端点位移相对误差则较大，基本都超出了工程精度20%的要求，故网络在工况3条件下代替集中质量法进行缆索截断点运动计算基本不可行。

表4 缆索Line4上端点位移统计结果(模型尺度)

图8 工况2、3 截断水深与全水深张力对比

工况2缆索Line4张力值统计结果(模型尺度)项目平均值最大值最小值标准差全水深结果(N)837E+00130E+01651E+00795E⁃01截断水深结果(N)833E+00145E+01577E+00829E⁃01相对误差046%1125%1142%422%工况3缆索Line4张力值统计结果(模型尺度)项目平均值最大值最小值标准差全水深结果(N)7817E+001015E+016785E+004278E⁃01截断水深结果(N)7680E+001652E+013758E+008612E⁃01相对误差175%6282%4461%10131%

表6 工况2、3缆索Line4上端点位移统计结果(模型尺度)

3 结论

结合主动式模型截断试验仿真的结果可以得到以下结论：

1)由工况1数据离线训练得到的NARX网络在工况1以及工况2下有着很好的性能，截断情况下用其代替集中质量法进行缆索截断点的在线运动计算，所得缆索张力及运动的统计结果与全水深情况下的结果基本相同。

2)工况3由于在波高以及谱峰周期与训练工况1相差较远，因此造成截断水深结果与全水深结果差异较大，由此可见NARX网络不能完全适用于所有工况下截断点运动的计算。

3)由于NARX网络计算所得位移与集中质量法结果存在偏差，从而使得截断水深情况下的缆索张力较全水深情况不能完全相同。截断点位移偏差也造成缆索张力存在明显的高频“毛刺”，而在实际试验中即使数值计算结果十分精确，截断点的执行机构存在的机械间隙也不能保证位置命令的精确执行，因此在实际中还需要引入相应的位置修正，使位移偏差尽量减小。

[1]Stansberg C T, Ormberg H, Oritsland O. Challenges in deep water experiments: Hybrid approach [J]. Journal of Offshore Mechanics and Arctic Engineering, 2002, 124(2): 90-6.

[2]Stansberg C, Karlsen S, Ward E, et al. Model testing for ultradeep waters[A]. proceedings of the Offshore Technology Conference, F, 2004[C].

[3]杨建民, 肖龙飞, 盛振邦. 海洋工程水动力学试验研究 [M]. 上海:上海交通大学出版社, 2008.

[4]洪文渊, 张火明, 管卫兵, et al. 系泊缆等效水深截断点处动力响应 [J]. 舰船科学技术, 2015(1):23-28.

[5]高文军. 深海系泊缆等效水深截断点处运动和受力的仿真及控制 [D].杭州：中国计量学院, 2012.

[6]Buchner B, Wichers J, De Wilde J. Features of the State-of-the-art Deepwater Offshore Basin[A]. proceedings of the Annu Offshore Technil Conf, F, 1999[C].

[7]Cao Y, Tahchiev G. A Study on an Active Hybrid Decomposed Mooring System for Model Testing in Ocean Basin for Offshore Platforms[A]. proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, F, 2013 [C]. American Society of Mechanical Engineers.

[8]王 琳, 马 平. 系统辨识方法综述 [J]. 电力科学与工程. 2001: 63-6.

[9]Guarize R, Matos N, Sagrilo L, et al. Neural networks in the dynamic response analysis of slender marine structures [J]. Applied Ocean Research, 2007, 29(4): 191-198.

[10]Uddin M, Jameel M, Razak H, et al. Response Prediction of Offshore Floating Structure Using Artificial Neural Network [J]. Advanced Science Letters, 2012, 1): 186-9.

[11]Walton T S, Polachek H. Calculation of transient motion of submerged cables [J]. Mathematics of computation, 1960, 14(69): 27-46.

[12]Mackay D J C. Bayesian Methods for Backpropagation Networks [J]. Physics of Neural Networks, 1996, 211-54.

Simulation of Active Truncated System Based on Neural Network

Zhang Longhui,Wei Naxin,Kuang Xiaofeng,Fan Yali

(China Ship Scientific Research Center, Wuxi 214082, China)

A cable numerical model with fast solution speed is required in active truncated system. Because of intermediate equilibrium iterations, numerical model based on lumped-mass method’s solution speed is slow. To solve this problem, neural network was used to get equivalent model in time domain which reflects the motion relationship between upper point and truncated point of cable. This network model do not need iterative process so its solution speed can be more faster than lumped-mass method. A simulation platform was built by using Orcaflex and Matlab. In the process of simulation, lumped-mass method was replaced by neural network which is got off-line to do on-line computation. Comparison with results between full-depth system and truncated-depth system, it shows neural network is feasible in active truncated system.

active truncated system; neural network; mooring system; cable dynamic

2016-07-28；

2016-08-31。

张隆辉(1990-)，男，福建福州人，助理工程师，主要从事试验检测技术方向的研究。

1671-4598(2017)01-0232-04DOI：10.16526/j.cnki.11-4762/tp

TP

A