基于改进权值和TOPSIS质量评估方法

孙希彤，刘秋生，王乐军

(1.军械工程学院三系，石家庄 050003；2.中国人民解放军66435部队，河北 承德 067000)

基于改进权值和TOPSIS质量评估方法

孙希彤1，刘秋生1，王乐军2

(1.军械工程学院三系，石家庄 050003；2.中国人民解放军66435部队，河北 承德 067000)

针对武器电子系统质量评估过程中客观性不强、实用度较差的问题，引入评估指标的区分度与重要度概念，提出基于DSmT改进权值的TOPSIS质量评估方法；首先，从主客观角度构建指标重要度和区分度作为广义信度赋值；然后采用DSmT(Dezert-Smarandache Theory)理论融合不同冲突证据源的广义信度赋值，消除证据源间的冲突，得到改进权值；接着构造基于改进权值的TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法隶属贴近度；最后，以某型感应装定器为例进行实验验证，结果表明，该方法确定的指标权重具有更高可信度，对系统的质量评估更加准确，符合装备实际情况，具有较好的工程应用价值。

改进权值；质量评估；隶属贴近度

0 引言

武器电子系统质量评估是一个选择指标、划分权重、给出评判的过程。现代质量评估中，指标权重确定一直是一个难以解决的问题，也是多决策领域专家关注与研究的重点。比较常用的权重确定方法[1]有主成分分析法、灰色关联度分析法[2]、粗糙集理论分析法、聚类分析法、信息熵权法和层次分析法[3]。不论何种方法，主要分为两大范畴。一类是基于人因的主观权重确定，一类是基于源数据的客观权重确定。诸如基于数据源信息熵的客观权重充分发挥了指标数据本身信息有效性，但缺乏人因指导。采用引入专家评判的模糊综合评估或层次分析法来获取指标权重，受主观臆测影响，一旦评判失误，会出现极大偏差。即便是主客观方法共同确定，也是人为主导，对于主客观指标权值结果的机械分配。

质量评估的另一个难点是如何准确合理的给出评估结果，评估结果能够符合评估对象实际。在心电、桥梁、电子系统、航空航天等领域已经开展了较多质量评估的研究，各类评估方法大多是针对评估对象的特点采用特定的评估方法，应用范围有限，移植扩展较难。其中，比较常用的评估方法有综合指数法、功效评分法、支持向量机、层次分析法、模糊综合评估法、聚类分析法、灰色关联度评估法[2]和人工神经网络法[4]。不同的评估对象，究竟采用何种算法评估需要工程试验，通过结果分析不断的反馈调整。缺乏一种适用范围广，通用性的质量评估方法。

针对指标权重缺乏科学的评判依据，质量评估方法普遍适用性不强的问题。现提出利用DSmT信息融合理论进行指标权重的确定，把指标权重看作高度冲突的证据源，按照证据源原有信度比例关系，将冲突信度重新分配组合，构建指标权重，实现基于信息熵的数据有效性和基于专家评判的专业知识性高效融合。提出利用TOPSIS法构造隶属贴近度，确定评估系统指标理想点和临界点，依据对理想点和临界点贴近度，实现质量评分，以此来判断武器电子系统是否可靠。该方法适用度大，通过理想点和临界点的调整，实现移植。

1 基于DSmT指标权重改进

基于信息熵的指标区分度确定，对数据源进行预处理，求取熵权值，获得指标间有用信息的相对大小；基于层次分析法(AHP)的指标重要度确定，充分发挥专家知识度优势，通常在相关领域内获得一致认可。两种证据源各有侧重，通过DSmT融合规则进行广义基本信度赋值合成，得到最优指标权值。

1.1 指标区分度确定

熵的概念最初是在热力学中提出，用于表示物质系统状态的物理量，表示该状态可能出现的程度，用来说明热学过程不可逆性的一个比较抽象的物理量。在信息论里则叫信息量，信息熵越大，数据提供信息就越多，即熵是对不确定性的度量[5]。熵可以表示为

(1)

式中，pi为对应概率。

在装定器评价指标中，各指标的竞争激烈性，可以用信息论中有用信息多少来确定各个指标的权重关系，即熵值越大，指标指向性越差，可用性越低，熵权越小，反之亦然。因此可用信息熵所获系统信息的有序度来确定指标权重，它能消除各指标权重计算时的人为干扰，使评价结果更客观。

在有n个实施方案，m个评估指标的评估问题中，原始数据矩阵X=(xij)n×m为

式中，xij为第i个方案的第j个评价指标。

为消除评价指标间的量纲影响，保证数据之间具有可比性，对原始数据进行标准化处理。以下是4种常用的归一化方法

Z-score标准化方法：

(2)

越大越优型标准化：

(3)

越小越优型标准化：

(4)

偏差型标准化：

(5)

式中rij为第i个方案的第j个评价指标标准化值，rij∈[0,1]；

xmax为指标的上限值或警戒值；

xmin为指标的下限值或警戒值；

xmav为指标的最优值；

xmean为指标样本数据均值；σx为指标样本数据标准差。

原始数据标准化后的矩阵R=(rij)n×m为

在n个方案，m个评价指标的评估问题中，第j个评价指标的熵定义为

(6)

式中

(7)

规定当fij=0时，fijlnfij=0。

求得每个指标的熵值之后，我们可以根据熵值计算指标熵权值。第j个指标熵权值定义为

(8)

熵权值表示采集数据的有效信息量，即指标区分度。当系统向着某个态势发展时，其指标变化越大，熵值越小，熵权值越大。因此熵权值能够反映该指标提供有用信息的多少。但是，指标区分度仅从客观数据的角度反映了有效信息量的多少。整个感应装定系统质量评估需要考虑架构设计、效能、结构功能等诸多因素。因此，对系统的评估需要多方面考量，下面基于层次分析法，从专家评判的角度，主观评定评价指标，进一步完善评价方法。

1.2 指标重要度确定

层次分析法(AHP)是美国运筹学家Saaty等于二十世纪70年代提出的一种多目标决策法。针对感应装定评价指标多、区分难度大的特点，采用0.5～0.9标度法[6] [3]，下表1列出了0.5～0.9标度的含义。

表1 判断矩阵0.5～0.9标度法含义

按照表1-1，n个实施方案，m个评估指标两两比较得到的判断矩阵A=(aij)m×m

式中，aij为第i个评价指标与第j个评价指标的标度值。

(9)

针对获得的判断矩阵A，计算最大特征根λmax及其对应的特征向量为

从式(9)得到的特征向量作为评价指标的权重向量。

判断矩阵的一致性检验采用K因子检验法，它是由Herman于1996年提出，该方法排除随机因素的影响，简洁有效。定义计算因子K(A)为

(10)

若K(A)≥K0，则A=(aij)m×m具有一致性。

基于层次分析法的指标重要度确定，依据专家对指标重要性的主观评判来进行评定，合理的确定了指标相互间的重要程度。但是，该算法受专家主观意识影响较大，一旦某位专家出现评判偏差，将造成评估结果的失真。为了减小评估失真，对各类赋权算法得到的权值进行数据融合，得到改进后的最优权值。

1.3DSmT融合理论

美国FlorentinSmarandache和法国JeanDezert于20世纪初提出的DSmT理论，是对经典的DST理论的扩展。两位作者将似是而非与自相矛盾的推理方法运用在信息融合领域[7]。为了使读者更加清楚的认识DSmT理论，便于合理的解决问题，由文献[8]给出DSmT理论的基本定义。

定义1 ：超幂集DΘ概念。

在DSmT框架中，Θ是一个包含n个完备命题{θ1,…,θn}的集合(也称为框架)。Dedekind格子模型，即DΘ，在DSmT框架中，称为超幂集。它是由Θ中命题，以及通过∪和∩的运算组成的所有的复合命题的集合，形式如下：

1)φ,θ1,…,θn∈DΘ；

2)如果A,B∈DΘ，则A∩B∈DΘ,A∪B∈DΘ；

3)除了(1)和(2)中包含的命题，再没有其他命题属于DΘ。

定义2 ：广义信度函数。

在广义框架Θ中，定义一组映射m(·):DΘ→[0,1]，它与证据源本身相关，具体满足下式：

(11)

式中，m(A)为A的广义基本信度赋值(GBBA)。

基于广义基本信度赋值m(A)，对于任何命题集，定义信度函数的概念为

(12)

定义3： 广义似然函数。

信度函数Bel(A)仅能描述我们对命题A信任程度，不能反映对A的怀疑程度。因此，定义似然函数Pl(A)为

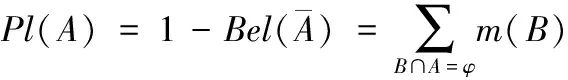
(13)

定义4 ：DSmT融合规则。

DSmT融合规则包含经典DSmT融合规则(DSmClassicrule)、混合DSmT融合规则(DSmHybridrule)和比例冲突分配原则(ProportionalConflictRedistributionRule)。比例冲突分配原则中，又包含五种PCR规则——PCR1～PCR5。目前公认的分配精度最高的是PCR5，因此，选取PCR5作为数据融合的原则是比较合理、准确的[9]。

DSm模型μf(Θ)解决融合问题时，独立证据源S1和S2经典DSm组合规则是mμf(Θ)(·)≡m(·)。它们的广义基本信度赋值为m1(·)和m2(·)，可作如下定义：

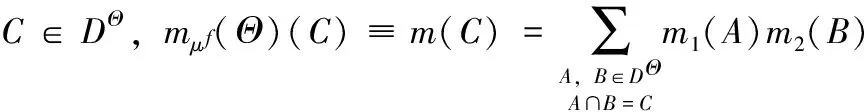
超幂集DΘ在∪和∩运算下是封闭的，其个数随着Θ势的增多而急剧增加。指标权重融合中，超幂集DΘ不需要过于精细的分类。利用PCR5分配理论进行冲突再分配再合适不过，其定义为

(14)

证据1的X1和证据2的X2的冲突，证据1的X2和证据2的X1的冲突，是证据间的两类冲突。按X1、X2原有信度的比例关系，PCR5将上述冲突信度分配到X1和X2的组合信度上[10]。

传统的权值确定，通常只是将客观权值与主观权值进行加性或乘性组合，组合过程也是以人为偏好来主导。该方法缺乏理论依据，易因人因而误导。DSmT理论可对冲突信度再分配，信息熵得到的指标客观权值和层次分析法获得的主观权值作为广义基本信度赋值，属性上存在冲突性。利用DSmT理论融合，获得兼有主观属性和客观属性的组合权值，实现权值优化。

2 TOPSIS法质量评估模型

C.L.Hwang和K.Yoon于20世纪80年代提出TOPSIS法[1]。它是根据各个评估指标值与理想化指标值的接近程度来进行评判的方法，实现现有系统相对优劣的评价。该方法只要求各效用函数具有单调递增(或递减)性即可。TOPSIS法常用于多目标决策分析中，又称优劣解距离法[11]。

确定评估指标最优解和最劣解，通过检测指标值与最优解、最劣解的欧氏距离来进行排序。

2.1 指标理想点与临界点确定

设评估方案为n，评估指标个数为m，则每个方案指标值为

qi=(qi1,qi2,…,qim),i=1,2,…,n

初始决策矩阵为

对初始决策矩阵归一化处理，得到无量纲规范化决策矩阵。

根据规范化决策矩阵每列指标值，确定每个指标的最优解和最劣解。通常每列最大值或系统指标实际能达到的极大值为理想值，每列最小值或系统指标实际能达到极小值为临界值。记理想点u+和临界点u-为

2.2 隶属贴近度排序

隶属贴近度是一个表征测量值靠近理想值并远离临界值的数学量。通过计算隶属贴近度，可以确定各个决策方案的优劣程度。

测量值到理想点的距离为

(15)

测量值到临界点的距离为

(16)

式中，ωj为DSmT融合最优权值；

(17)

3 实例分析

3.1 构建评估指标体系

针对信息化弹药感应装定器，构建各级指标体系。针对该系统特点，确定质量评估从信号特性和内部电源特性两大方面进行评价，信号特性和电源特性再细分成各项具体参数，如图1所示。

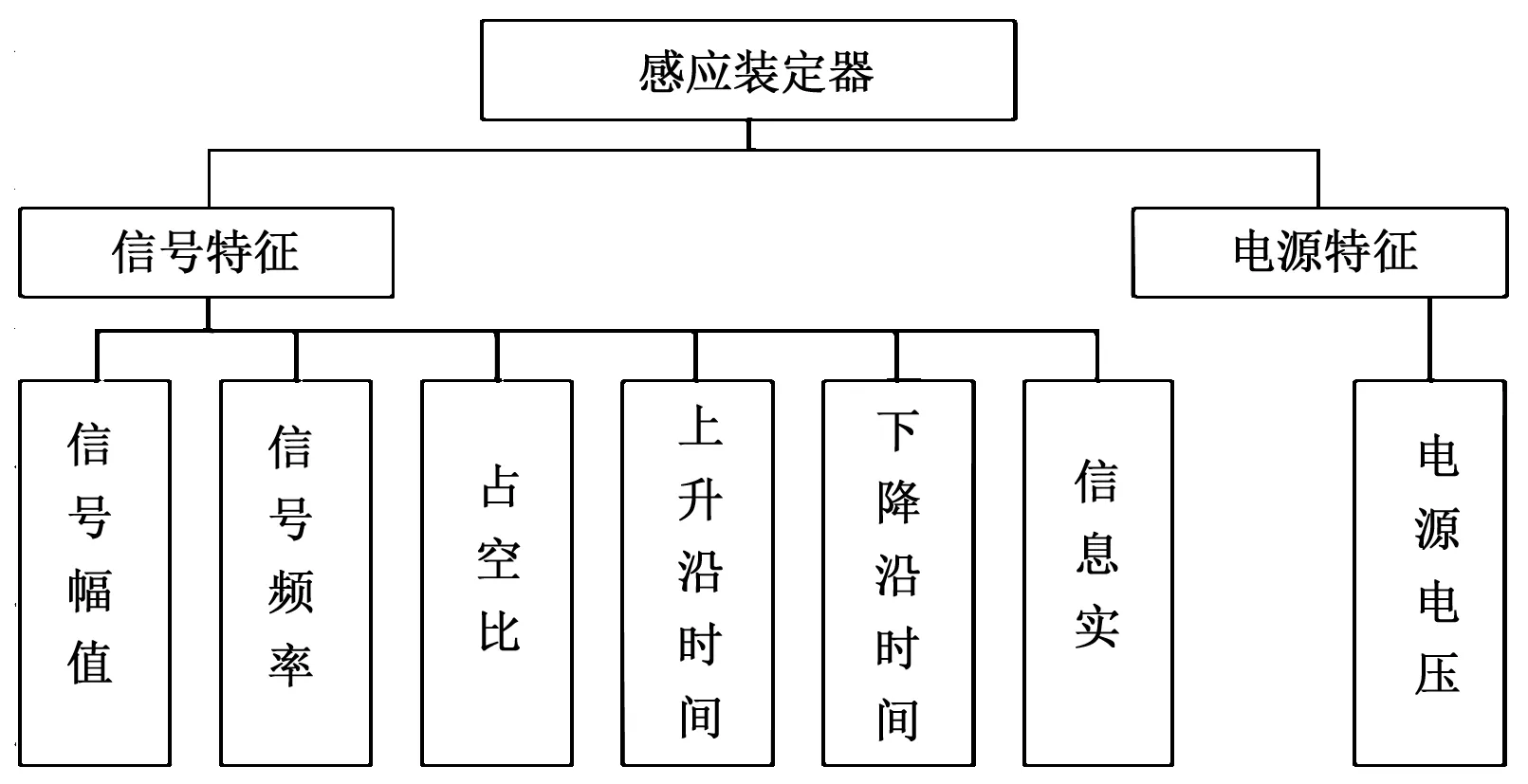
图1 质量评估指标体系

从图中看出，感应装定器质量评估因素集为：U={u1,u2}={信号特性，电源特性}，为一级评估因素集；每个一级因素集元素ui又包含n个指标，即ui={ui1,ui2,…,uin}，其中uij为第i个一级元素的第j个评价指标，为二级评估因素集。

3.2原始数据标准化

对感应装定器进行质量评估的评价指标值单位量纲不同，为便于不同量纲指标值融合，保证质量评估的可行性，需要将采集系统采集到的原始数据按式(2)～(5)进行归一化处理，将有量纲数据转换成[0,1]范围内的无量纲数据。每隔相同时间，采集一次数据。对每次采集的数据进行编号，按时间由近及远依次编为1、2、3、4。归一化处理后的数据列于如下表2中。

表2 质量评估指标归一化数据

3.3 权重确定

从感应装定器综合评估的角度，利用信号特征和电源特征的指标共同确定各评价指标的权重。首先对各评价指标数据进行归一化，得到各个指标处理后的信息量组成的矩阵F：

由计算公式(6)、(7)计算可得评价指标熵值，即区分度为：

根据式(8)求得指标熵权值为：

由多年从事该武器系统研究的专家对评判指标进行相对重要性比较，得到判断矩阵为：

从判断矩阵中可以得出，武器电子系统评价指标的重要性排序为u21>u11>u16>u13>u14>u15>u12。根据判断矩阵，由公式(9)计算最大特征值为λmax=3.1867，特征向量W=(0.4754,0.1964,0.3571,0.2990,0.2495,0.

4117,0.5356)T，一致性检K(A)=1.769。

对于判别阈值K0，Herman及业界专家通常取0.9，因此本文也取0.9。K(A)≥0.9，满足一致性。

特征向量W归一化，得感应装定器各指标权重为：

利用式(14)融合感应装定器评价指标权值，得到最优权值如下：

ω=(0.1905,0.0438,0.1266,0.0917,0.0895,0.1768,0.2811)T

3.4 可靠性确定

感应装定系统指标归一化处理满足单调递增性。当系统工作在最佳状态时，各个指标值归一化数据为1；当单一指标恰好使系统不能工作时，指标值归一化数据为0。因此，确定感应装定器理想点和临界点为：

u+=(1,1,1,1,1,1,1)

u-=(0,0,0,0,0,0,0)

由公式(15)(16)(17)，分别计算感应装定器指标测量值与理想点、临界点以及隶属贴近度结果。在装定器的每个采集阶段，邀请行业内从事多年装定器研究的专家对装定器整体质量评分。所得数据如表3所示。

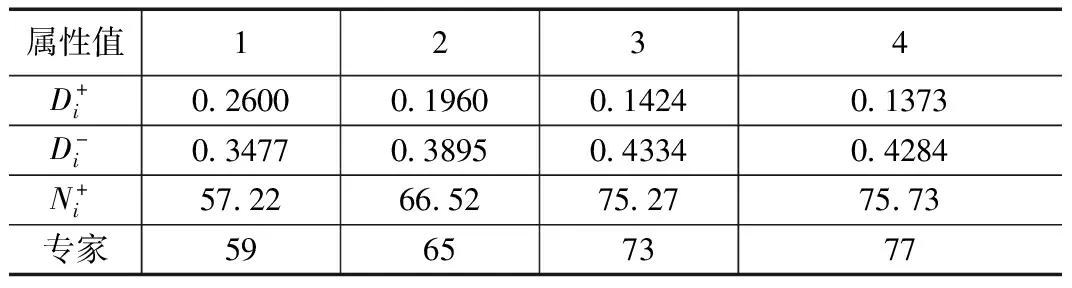
表3 感应装定系统距离值及隶属贴近度

由TOPSIS法得到的感应装定器隶属贴近度与专家评分按时间由远及近(即4、3、2、1的顺序)绘制于折线图2中。隶属贴近度即感应装定器质量评估得分。

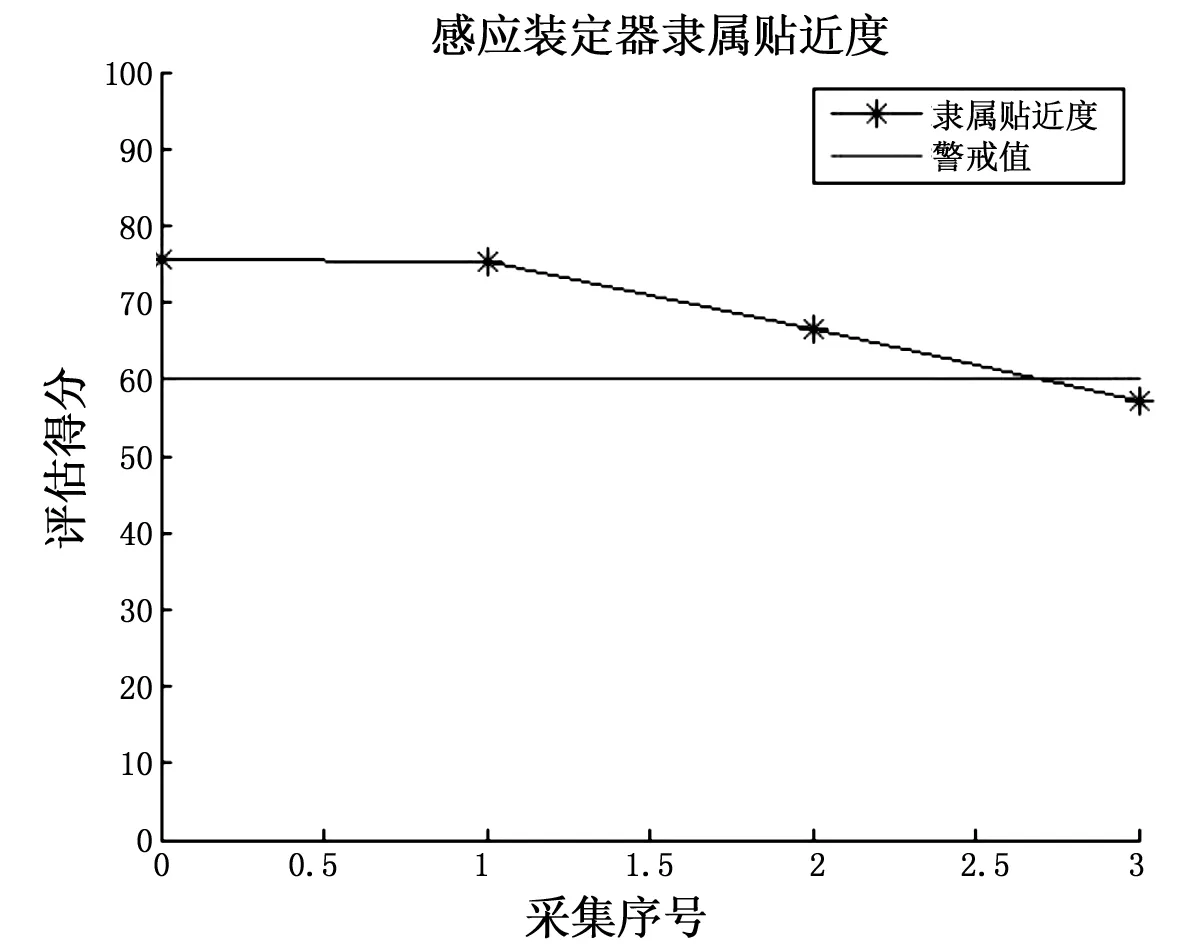
图2 感应装定器隶属贴近度

从折线图可以看出，最初，质量恶化速度缓慢，随后恶化速度加快，最终感应装定器质量得分低于警戒值，系统不能可靠使用。这一结果也符合事实情况。感应装定器质量变差的过程是缓慢的，一旦恶化到一定程度，达到某个临界状态，恶化程度会明显加速，最终报废失效。经过检查，最终评分低于警戒值的原因为感应装定器长时间使用，电量不足，指标值低于阈值。评估结果与实际一致。

4 结论

在研究武器电子系统质量评估过程中，提出了指标融合权值的概念，利用DSmT理论对指标区分度和重要度优化，实现了主观权值和客观权值相互冲突再分配。提出使用TOPSIS法进行武器电子系统质量评估，该方法普适性强。实例验证表明，本文提出的质量评估方法客观合理地评估装定器质量状态，评估结果符合装定器实际状态，对装定器失效状态判定准确，具有良好的工程应用价值。同时，该方法计算量小，移植性好，可用于多种系统质量评估。

[1] Abdou,Samir,Savoy,Jacques.Statistical and comparative evaluation of various indexing and search models[J].Lecture Note in Computer Science,2006:362-373.

[2] 邓聚龙.灰色理论基础[M].武汉：华中科技大学出版社，2002.

[3] 巩在武.不确定模糊判断矩阵理论方法研究[D].南京:南京航空航天大学,2006.

[4] 尚 鑫，徐 岳，马保林，等.基于神经网络的混凝土斜拉桥健康状态评估[J].武汉理工大学学报,2011,33(8):80-83.

[5] Shamilov,Aladdin.A development of entropy optimization methods[J].WSEAS Transactions on Mathematics,May,2006:568-575.[6] 曹 菲，曹 海，朱晓菲，等.武器电子系统质量评估[M].西安:西安电子科技大学出版社，2014.1:19-22.

[7] Dezert J.,Foundations pour une nouvelle theorie du raisonnement plausible et paradoxal[Z]. ONERA Tech.Rep.RT 1/06769/DTIM,Jan.2003.

[8] Dezert J,Smarandache F.Advances and Applications of DSmT for Information Fusion(collected works) [M]. America: University of Microfilm International,2004. 18-25.

[9] 于小红，周庆军，李艳丽，等.DST与DSmT自适应融合算法研究[J].计算机与数字工程，2013,41(1):35-37.

[10] 邱文昊，连光耀，张西山，等.基于DSmT和模糊综合评判的健康状态评估方法[J].计算机测量与控制，2015,23(11):3697-3700.

[11] 韩晓明，吴振亚，甘林海，等.改进型TOPSIS在航空动力系统质量评估中的应用[J].数学的实践与认识，2015,45(10):69-76.

Method of Quality Assessment Based on Improved Weight and TOPSIS

Sun Xitong1，Liu Qiusheng1，Wang Lejun2

(1.Third Department, Ordnance Engineering College,Shijiazhuang 050003,China；2. 66435 Troop,Chengde 067000,China)

Considering the problem of lower applicability and objectivity of Quality assessment for weapon electronic systems,the paper proposed a new method of quality assessment based on TOPSIS and index weight improved by DSmT.Firstly, discrimination and importance degree of index are as the basic belief assignment from the subjective and objective point of view.Then the basic belief assignment was combined to get the optimal weight by using DSmT. Membership of TOPSIS is constructed based on the optimal weight.Finally,the new method was used to evaluate a induction setter.The results indicate that the method can get good efficiency on the system quality assessment and it is in line with the actual situation of equipment.The improved weight is more credible.The method has great value in engineering application.

improved weight;quality assessment; membership

2016-05-12；

2016-08-24。

军内科研(ZS2014070132A12006)。

孙希彤(1991-)，男，山东滨州人，硕士研究生，主要从事信息感知与控制方向的研究。

1671-4598(2017)01-0228-04

10.16526/j.cnki.11-4762/tp.2017.01.063

TP306

A