改进的SURF彩色遥感图像配准算法

李少毅，王晓田，杨 开

(西北工业大学 航天学院，西安 710072)

改进的SURF彩色遥感图像配准算法

李少毅，王晓田，杨 开

(西北工业大学 航天学院，西安 710072)

为了进一步提高彩色遥感图像的配准精度，针对遥感图像配准过程中色彩信息利用率低以及误匹配率高的问题，提出一种改进的SURF(Speeded Up Robust Feature)彩色遥感图像配准算法;该算法首先在对彩色遥感图像进行特征点检测基础上，对特征点描述算子进行改进，以使颜色空间变换后得到的特征点色彩信息添加到原描述算子中,并对特征点描述算子进行归一化处理，以增加算子的独特性和对旋转、尺度、光照的鲁棒性；其次，结合单向匹配和双向匹配的比值，提出了一种最优化阈值选择准则，如果欧氏距离比率小于最优化阈值，完成特征点匹配，得到正确匹配点对，再通过变换矩阵得到配准图像;实验结果表明，在保证实时性的条件下，该算法相比于原SURF算法，准确性和稳定性都有一定提高，具有一定的理论和应用价值。

图像配准；改进描述符；最优阈值

0 引言

随着对遥感数据需求的急剧增加，与之密切相关的遥感图像配准技术也逐渐成为研究的热点，并已被广泛应用于遥感图像处理、目标识别、医学影像分析、机器视觉、以及三维重建等诸多学科和领域[1]。

目前，图像配准算法分为两类：基于区域灰度的配准方法和基于特征的配准方法。基于区域灰度的配准方法计算复杂，对图像平移、旋转、仿射变换都比较敏感，而基于特征的配准方法有效克服了以上缺点，尤其点特征在配准实时性和精确性方面具有明显优势，成为研究的热点。近几十年来，研究者们在基于特征点图像配准研究中取得了巨大突破，相继提出了Moravec算法[2]、Harris算法[3]、SUSAN算法[4]和SIFT(scale invariant feature transform)算法[5-6]。SIFT算法不仅对于旋转、平移、缩放等变换具有不变性，对于仿射变换模型也具有很强的鲁棒性，而且可以在多尺度空间进行特征点检测，可以消除尺度变化对配准的影响，同时光照对其影响也较小，在配准实时性和精确性方面明显优于其他算法[6]。2006年，在SIFT算法研究的基础上，Bay[7]等人引入了积分图像[8](Integral Image)和盒子滤波[9](Box Filters)的概念，提出了SURF(speed up robust features)算法，该算法的主要优点是保持了SIFT高鲁棒性的同时，使得配准时间在很大程度上得到优化，它实际上是SIFT的加速版。然而，基于特征点的配准算法对于彩色图像的配准大部分是将彩色图像变换成灰度图像，仅利用图像的亮度信息进行配准，没有充分利用图像的色彩信息。文献[10]提出了将RGB分量的强度归一化后再用SURF算法来处理彩色图像，此算法具有部分几何不变性，但描述色彩不变特征时仍有局限性。文献[11]提出了一种基于颜色不变量的SURF配准算法，此算法充分利用了图像的颜色信息，但算法耗时较长，实时性差，没有考虑特征点自身的色彩信息。

本文针对遥感图像配准过程中色彩信息利用率低以及误匹配率高的问题，提出一种改进的SURF彩色遥感图像配准算法，克服了原SURF算法特征点少和没有充分利用色彩信息的问题，在保证实时性的条件下，准确性和稳定性得到了一定的提高。

1 经典SURF算法原理

SURF算法包括特征点检测、特征点描述和特征点匹配三部分。

特征点检测是SURF算法的基础，特征点检测是在尺度空间金子塔的基础上，对DoH(determinant of hessian)进行简化和近似，并利用积分图像快速提取图像中的特征点的过程。

DoH特征点检测原理如下：设X=(x,y)为图像I(x,y)中的某一点，它在尺度σ上的Hessian矩阵定义为：

(1)

(2)

为了降低特征点提取过程的复杂度，提高实时性，采用盒子滤波和积分图像的概念，对Lxx(X,σ)、Lxy(X,σ)和Lyy(X,σ)进行简化和加速。盒子滤波近似地代替高斯二阶微分，用Dxx(X,σ)、Dyy(X,σ)、Dxy(X,σ)简化模板分别代替x方向、y方向和xy方向的高斯二阶微分滤波结果。下面给出对于σ=1.2高斯二阶微分滤波对应的大小为9*9的xy方向盒子滤波，如图1所示。

图1 盒子滤波简化xy方向滤波示意图

Hessian矩阵的行列式：

(3)

特征点由尺度空间金字塔中局部极值点组成，具有尺度不变性。

特征点描述是利用特征点周围邻域的梯度方向分布特性，为每个特征点指定方向参数，从而使描述子对图像具有旋转不变性。

像素点的梯度分布特性和描述向量构造通过进行Haar小波响应计算，Haar小波响应示意如图2所示。

图2 Haar小波响应和Haar小波模板

选定特征点主方向后，沿主方向将特征点周边矩形区域划分4*4=16个子块，利用Haar模板进行响应值计算，得到沿主方向的dy和垂直于主方向的dx，对每个子块的响应值进行统计，得到对每个子块的矢量：

(4)

如图3所示，描述符向量由特征点周围所有子块的向量构成，特征描述符向量长度便为4*4*4=64维，生成的描述符向量记为：

(5)

其中:Vi(i=1,2,3,...,15,16)表示16个子块所对应的描述向量。

图3 特征描述符的构造

特征点匹配过程是在两个特征点集中按照某种相似性度量准则搜索相互距离最近的特征点的过程。本文所使用的相似性度量准则为最近欧氏距离与次近欧氏距离比值的度量准则。

对于目标集中每一个特征点，在基准集中查询得到它的最近邻disnt和次近邻dissnt，若满足：

(6)

则保留这个特征点与其最近邻构成的匹配点对，否则剔除这个匹配点对。公式中的T是判断阈值，一般在0.4-0.8之间取值，多数算法中选择0.8。

最后采用随机抽样一致性算法(RandomSampleConsensus,RANSAC)提纯匹配点对，求取满足最小二乘意义下误差最小的变换矩阵，得到精确的图像变换模型，实现配准。

2 SURF算法的改进

SURF算法在对特征点进行描述时，仅利用特征点周围邻域的灰度信息进行描述，忽略了它自身色彩信息，为提高配准精度，需将色彩信息加入描述向量，以提高特征点差异性。

2.1 特征点描述向量的改进

特征点自身色彩信息根据颜色空间不同参数值也不相同。颜色空间中最为经典的颜色模型即为RGB模型。彩色遥感图像一般被分成R、G、B的成分并加以保存的。然而，在自然环境下获取的一些彩色遥感图像对亮度比较敏感，即RGB颜色空间的分量与亮度密切相关。即只要亮度改变，3个分量都会随之相应地改变。所以，RGB颜色空间适合于显示系统，却并不适合于图像处理。如果用它来表述特征点色彩信息，亮度差异造成配准误差较大。

HSV模型属极坐标空间定义的颜色模型，是以近似于人心理上能感知的特性作维数形成的空间，如色度、饱和度、亮度。该模型可以适应光照强度不断变化的场合，因此能够有效地用于彩色图像处理。

RGB颜色空间转换到HSV颜色空间的变换为：

(7)

下面对改进具体过程进行介绍，坐标为(x,y)特征点，其在RGB颜色空间表示为R(x,y)、G(x,y)、B(x,y)，将其进行颜色空间转换，转换到HSV颜色空间为H(x,y)、S(x,y)、V(x,y)。

将其增加到原始算法描述符中，得到新的彩色描述符如下：

(8)

为使表述更加清晰，将(4)式进行简单变换:

(9)

随后对公式(8)式进行重新定义如下：

(10)

为了对旋转、尺度、光照有更好的鲁棒性。需对得到的改进描述向量进行归一化处理：

(11)

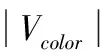
(12)

从公式(11)中可以看到，特征点自身的彩色信息被加载进来，构成了67维的描述向量，和原来的算法相比，时间上没有太大变化，但性能上因为考虑色彩信息，差异性增加，使得精度会进一步提升。

2.2 特征点匹配阈值的优化

考虑到现实生活中处理的图像种类繁多，不尽相同，因此对阈值T的需求也会有所差别，阈值设置为固定值便会显得不太合理，没有普遍的实用性，因此这里我们提出一种最优化阈值选择准则，使其对不同种类图像都有一定通用性。在保证特征点对足够多的基础上，错误匹配点对最大程度上被压制，从而提高配准精度。

大量学者采用最近邻/次近邻方法匹配，可以得到单向匹配特征点对，但会导致多对一的匹配，随着特征点数量的增加，误匹配率也增加。

双向匹配可以很好的剔除误匹配点对，主要思想是基于最近邻/次近邻匹配的基础上，从图像image1到图像image2对特征点进行遍历搜索匹配，然后从图像image2到图像image1进行遍历搜索匹配，将检测结果一致点对保留下来，否则，将其删除，从而实现特征点一对一的匹配。

本文将双向匹配点对/单向匹配点对比值作为最优化阈值选择的准则，在判断阈值T(0.4～0.8)选定时，单向匹配点对足够多，双向匹配检测到的误匹配点对足够少时，选定的阈值即为最优阈值，具体步骤如下：

首先，结合判断阈值T选取范围确定搜索区间为0.4～0.8，根据实验经验，实际中公差选为0.02效果最佳。

然后，对于任意选定的阈值T0=0.4+0.02*k(k=1,2,...20),计算双向匹配点对数N与单向匹配点对数M的比值。

最后根据双向匹配点对数M与单向匹配点对数N的比值，最大值对应的T0即为最优阈值，记作：Toptimal=T0，由此，就得到最优阈值。

2.3 基于改进SURF算法的遥感图像配准

改进算法流程图如图4所示：

实现步骤如下：

1)利用Hession矩阵的行列式对参考图像和待配准图像进行特征点检测，同时对于所找到的特征点进行描述，形成64维描述向量；

2)特征点自身色彩信息加入描述向量中，利用颜色空间变换将特征点R、G、B分量值转换成H、S、V分量，构成67维包含色彩信息的描述向量，增加差异性；

3)对特征点描述向量归一化，增加鲁棒性；

4)利用单向匹配点对和双向匹配点对的比值，作为最优化阈值选择的准则，在保证特征点对足够多的基础上，最大程度上压制错误匹配点对，从而提高配准精度。结合最近邻与次近邻比值小于最优阈值的度量准则实现特征点匹配；

5)RANSAC算法提纯匹配点对，求取变换矩阵，实现配准。

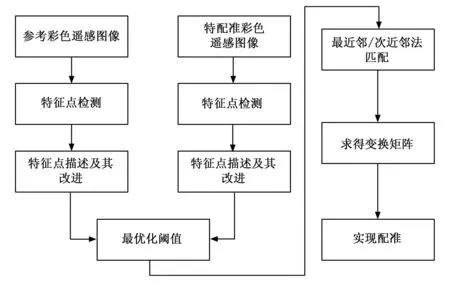
图4 改进SURF算法流程图

3 仿真分析与比较

为了证明算法的可行性及其性能，本文用彩色遥感图像对其进行仿真验证。试验中仿真平台的硬件环境为：AMDA8-4500MAPUwithRadeon(tm)HDGraphics，2.00GHz，4.0GB内存的PC机；软件开发工具为：Windows7操作系统，MATLAB2013a。

实验参数特征点检测阶段尺度空间构建为5组，高斯模板为0.33。

3.1 实验及结果

如图5所示的两幅遥感图像，image1和image2分别被称为待配准图像和参考图像，使用SURF算法和本文改进SURF算法对彩色遥感图像进行匹配。

图5 彩色遥感图像配准图

客观上用提取特征点数量，正确匹配点对与正确率，以及时间3个指标进行评价。如表1、表2所示分别给出了特征点对比分析表以及时间评价表，可以看出本文改进方法在待配准和参考图像提取特征点数量分别为383个和307个，匹配点对38对，正确率高达96%，明显优于SURF算法；时间上有一定增加，但是相对于精度上的提高，是值得的。所以综合上述两个方面进行评价分析可知，本文改进算法整体上提高了配准图像质量[13-14]。

表1 特征点对比分析表

表2 时间评价表

3.2 仿射变换验证精度

彩色遥感图像image1和image2之间几何变换关系固定，可以很容易的得到理论值变换矩阵Hture。利用改进SURF彩色遥感图像配准算法代码与SURF原作者推荐的代码，按照默认参数进行配准，求取待配准图像相对于参考图像的仿射变换矩阵Himprove和Hsurf，并与实际真实值进行对比，与真实值越接近，仿射矩阵求取精度越高，仿射变换中参数m7、m8和m9默认为0、0和1。由于该算法当中涉及随机数选取过程，只用一次仿真结果无法准确反映实验结果，这里对这两幅无人机遥感图像进行十次仿真实现，取各参数平均值，十次仿真实验参数取平均值后具体数据如表3所示。

从以上数据可以看出，按照原作者提出算法对彩色遥感图像配准求取出的仿射变换矩阵，6个参数与真实数据都有一定的偏差，偏差较大，最大偏差0.433 0。本文改进SURF图像配准方法求取出的仿射变换矩阵，6个参数与真实数据都非常接近，最大的偏差只有0.120 4，精度明显高于原作者提出的

表3 仿射变换矩阵参数

算法。不失一般性，随后选取八对无人机遥感图像分别进行试验，得出相同的结果，原作者提出的算法其最大偏差平均值为0.218高于改进的最大偏差平均值0.134，六参数接近程度改进算法明显优于原作者提出的算法，可见对于彩色遥感图像进行配准，改进算法很大程度上使得配准精度得到提升。

3.3 归一化互相关测度验证精度

归一化互相关算法通过比较两幅图像之间的归一化互相关来判断配准结果优劣[12]。首先将待配准图像仿射变换到参考图像坐标系，这时就满足归一化互相关条件，适合于具有平移和小角度旋转关系的图像配准，从该图像中截取一部分作为模板求取它与参考图像的相关程度，以此作为判断配准精度的准则。

由图6我们可以发现归一化互相关可以实现最终配准，但是从配准的效果图我们可以很方便的判断改进的配准效果明显优于原作者的算法，原算法在两幅图叠放边缘明显存在错位。而且根据归一化公式[12]我们可以很方便的求取原SURF算法和改进SURF算法归一化互相关峰值分别为0.816 3和0.960 3，这里的归一化互相关数值越大，精度便越高，所以改进SURF算法配准效果明显优于原算法。

图6 彩色遥感图像归一化互相关评价

4 结束语

本文提出了一种鲁棒的SURF彩色遥感图像配准算法，在特征点描述阶段通过彩色空间变换充分利用彩色遥感图像的色彩信息，增加特征点描述符的独特性和对旋转、尺度、光照鲁棒性；在特征点匹配阶段，结合单向匹配和双向匹配的比值，提出了一种最优化阈值选择准则，提高匹配精度。实验结果表明，该算法在保证算法实时性基础上，彩色遥感图像配准准确性和稳定性都有一定提高。对于多源遥感图像配准问题和红外制导导弹末制导配准问题是下一步研究的方向。

[1] 温红艳. 遥感图像拼接算法研究[D]. 武汉: 华中科技大学, 2009.

[2] Thangavel P K, Kokila R. An extension of FFT based image registration[J]. Advances in Intelligent Systems and Computing, 2013, 177(2): 729-737.

[3] Harris C G, Stephen M. A Combined Corner and Edge Detector[A]. Proceedings of the Fourth Alvey Vision Conference[C].1988: 8-12.

[4] Smith S M, Brady J M. SUSAN: A new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45-78.

[5] Linderberg T. Feature detection with automatic scale selection[J]. International Journal of Computer Vision, 1998, 30(2):79-116.

[6] Lowe D G. Object recognition from local scale-invariant features[A]. Proceedings of International Conference on Computer Vision[C]. 1999: 1150-1157.

[7] Bay H, Essa A, Tuytel A T. Speeded-up Robust Features(SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359.

[8] Simard P, Bottou L, Haffner P. Boxlets: a fast convolution algorithm for signal processing and neural networks[C]. Proceedings of the 1998 Conference on Advances in Neural Information Processing Systems, 1999:571-577.

[9] Viola P, Jones M. Rapid object detection using a boosted cascade of simple features[C]. Conference on Computer Vision and Pattern Recognition, 2001: 511-518.

[10] Lowe D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(3): 91-110.

[11] Fan Peng, Men A D, Chen M Y, el al. Color-surf: a surf descriptor with local kernel color histograms[A]. IEEE Computer Vision and Patter Recognition[C]. 1999, (2): 726-730.

[12] Pan W H, Wei S D, Lai S H. Efficient NCC-based image matching based on novel hierarchical bounds[J]. Lecture Notes in Computer Science, 2008(468):807-815.

[13] 张 永, 武玉建. 一种改进的SIFT图像特征匹配算法[J]. 计算机工程与应用, 2014, 50(9): 167-170.

[14] 张永梅， 张晨希，巴德凯. 改进SIFT变换与客观评价结合的图像配准算法[J]. 计算机测量与控制, 2015, 23(6): 2090-2093.

An Improved Surf algorithm for Color Remote Sensing Image Registration

Li Shaoyi，Wang Xiaotian，Yang Kai

(College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

To further improve the registration precision of color remote sensing image, an improved SURF registration algorithm is put forward aiming at solving the problem of low utilization rate of color information and high share of wrong matching pairs. Firstly, a modified descriptor is constructed adding in color information to increase the descriptor’s distinctiveness and robustness. Secondly, combined with the ratio of one-way matching and two-way matching, an optimal threshold method is put forward to increase the accuracy. If the Euclidean distance ratio is less than the optimal threshold, the correct matching points could be acquired. And the registered image was obtained based on transformation matrix. Experimental results show, compared with the original SURF algorithm, that the improved algorithm has certain improvement in terms of accuracy and stability while guaranteeing the real time. It has certain values in both theory and practice.

image registration; modified descriptor; optimal threshold

2016-10-30；

2016-12-05。

上海航天科技创新基金(SAST2016073)。

李少毅(1986-)，男，陕西西安人，博士后，主要从事图像处理与目标识别方向的研究。

1671-4598(2017)01-0209-04

10.16526/j.cnki.11-4762/tp.2017.01.058

E926.3

A