基于经验模态分解和小波阈值的冲击信号去噪

苏秀红，李 皓

(中国工程物理研究院总体工程研究所，四川 绵阳 621900)

基于经验模态分解和小波阈值的冲击信号去噪

苏秀红，李 皓

(中国工程物理研究院总体工程研究所，四川 绵阳 621900)

冲击信号是非线性的并且容易受到噪声污染；为研究冲击信号去噪的问题，针对经验模态分解(EmpiricalModeDecomposition,EMD)去噪和小波阈值去噪方法存在的不足，提出了基于EMD的小波阈值去噪方法；单纯的EMD去噪方法会在去除高频噪声的同时压制高频的有效信息；EMD与小波阈值去噪相结合，利用连续均方误差准则确定含噪较多的高频固有模态函数(IntrinsicModeFunction,IMF)，对高频IMF分量进行小波阈值去噪，以分离并保留这些分量中的有效信息，同时保持低频IMF分量不变；对模拟数据和实际冲击信号进行去噪处理，结果表明，基于EMD的小波阈值去噪方法的去噪效果优于单纯的EMD去噪方法和小波阈值去噪方法。

小波阈值；经验模态分解；冲击信号；去噪

0 引言

军用产品及其部件在运输、发射、飞行、使用的过程中都会受到机械冲击的作用。因此在产品的研制过程中，冲击试验是必不可少的考核项目。冲击试验包括爆炸分离、跌落等试验项目，主要考核产品的结构特性、评定产品对于冲击环境的适应性。实际的冲击试验现场环境比较恶劣，为了保证试验的安全性，记录仪器到测试用传感器之间一般存在一定距离，实际冲击信号采集过程中易受试验环境和测试系统的影响，测试信号中混杂噪声的情况不可避免，这会影响振动信号的特征提取。因此，如何去除冲击信号中的噪声，提高测试数据的可靠性和准确性，是冲击信号分析研究的基础。

希尔伯特黄变换是Huang提出的一种时频分析方法[1]，它是一种自适应的时频分析方法，不需要事先选定基函数，可根据信号的局部时变特征进行自适应的时频分解，具有很好的时频分辨率，因此非常适合于非平稳信号的分析。EMD作为希尔伯特黄变换的第一步，指的是将信号分解为有限数目频率依次递减的IMF，该方法是从信号本身的尺度特征出发对信号进行分解，因此是后验的。EMD作为处理非平稳信号的有效方法，已被成功应用到力学、信号分析等多个领域，基于EMD的信号去噪也被广泛研究。文章[2]利用EMD对脉冲类电磁噪声进行压制处理，引入阀值的概念对IMF进行处理，实测数据表明此方法可以有效抑制噪声干扰；文献[3]提出一种基于EMD和互信息熵的强噪声背景下的微震信号提取方法。

小波变换作为一种比较成熟的信号分析方法，因其具有多尺度性、去相关性和低熵性等特性，在信号去噪方面应用广泛，特别是在随机噪声的压制上具有很好的效果。Donoho[4]在1995年提出基于小波分析的阈值去噪方法，该方法在Besov空间上可得到最佳估计值，因此，在信号去噪领域得到了广泛的应用。基本的收缩函数包括软阈值函数和硬阈值函数，这两种阈值函数在信号降噪处理中效果不错，但在连续性和逼近原始信号方面存在一定缺点。针对此，文献[5-8]分别提出不同的改进阈值函数，并通过仿真验证了改进阈值函数的性能提升。

本文将小波阈值函数去噪的方法与EMD分解方法相结合，引入连续均方误差准则获取能量分界点，以确定需要降噪的高频IMF分量，只对高频IMF分量进行小波阈值去噪，保持低频IMF分量不变，通过信号重构获得降噪后的信号。模拟数据仿真和试验研究均能验证本文所提联合去噪方法的性能提升。

1 方法原理及步骤

1.1 EMD方法

经验模态分解又称huang变换，该方法不需要事先选择基函数，它根据信号的局部时变特征进行自适应的时频分解。EMD方法将原信号x(t)分解为一系列IMF分量Ci和一个残余项rn的和[9]，即：

(1)

式(1)中Ci表示各阶IMF，rn为残余项。Ci一般通过包络拟合的方式求得，分别代表了原始信号中不同时间尺度上的特征信号。

1.2 小波阈值去噪

小波阈值去噪首先将信号变换到小波域，在小波域内进行阈值处理，压制包含随机噪声的小波系数。最后通过小波系数重构，得到去噪后的信号。阈值处理方法包括硬阈值和软阈值方法，硬阈值方法是保持高于阈值的小波系数不变，将各子空间低于阈值的小波系数置零；软阈值方法是将小波系数按某一固定量向零收缩，由新的小波系数进行重构得到去噪后的信号。硬阈值表达式为

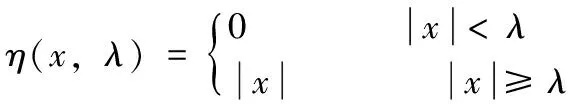
(2)

软阈值函数的表达式为

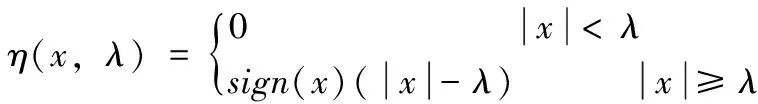
(3)

2 基于EMD的小波改进阈值去噪

2.1 联合去噪算法

由于EMD去噪方法是舍弃一个或多个的高频分量，因此在去除高频噪声的同时也将相应分量上的有效信息一并去除，进而导致信号的严重失真[11]；而小波阈值去噪的方法在去除大部分噪声的同时，会将小幅度的有效信号一并去除。本文将EMD和小波阈值去噪结合在一起，首先将信号进行EMD分解得到频率由高到低的IMF分量，只对高频分量进行小波阈值去噪，保持低频IMF不变。最后将去噪后的高频IMF和低频分量以及残余量合并，即得到去噪后的信号。

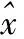
(4)

式中Ci(t)为信号x(t)经EMD所得的第i个IMF分量。信号的连续均方误差定义为[12]：

(5)

其中N为信号x(t)的长度，Ck(t)为信号x(t)经EMD分解后所得的第k个IMF分量。基于以上分析，可以确定信号能量分界点为：

(6)

确定分界点Cis之后，对划分出的高频段内IMF分量进行小波阈值去噪，而低频段内IMF分量则认为其不含噪声，不作去噪处理。这样既可以避免直接舍弃高频分量造成的有用信息丢失，同时由于小波去噪仅作用于高频IMF分量，因此能够较大程度克服小波阈值去噪的缺陷。基于以上分析，本文提出的去噪算法的具体步骤如下：

1)对受干扰的振动信号x(t)进行EMD分解，得到各模态分量Ci；

2)根据连续均方误差准则，确定is的取值；

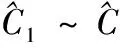
算法相应的流程图见图1。

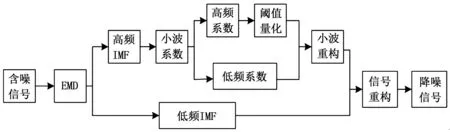
图1 基于EMD的小波阈值去噪方法流程图

2.2 模拟信号仿真分析

为了验证所提去噪算法的性能，在对实测冲击信号进行去噪处理之前，首先在Matlab环境下构建信号模型，对模拟含噪信号分别用EMD低通去噪法、小波阈值去噪法和本文提出的去噪方法进行仿真。模拟非平稳信号采用仿真模拟地震Ricker子波，Ricker子波的数学表达式为：

(7)

上式中，f(t)为振幅，fp=50 Hz为谱峰频率。信号在去噪之前叠加高斯白噪声。不加噪声的Ricker子波初始信号和含噪噪声如图2和图3所示。

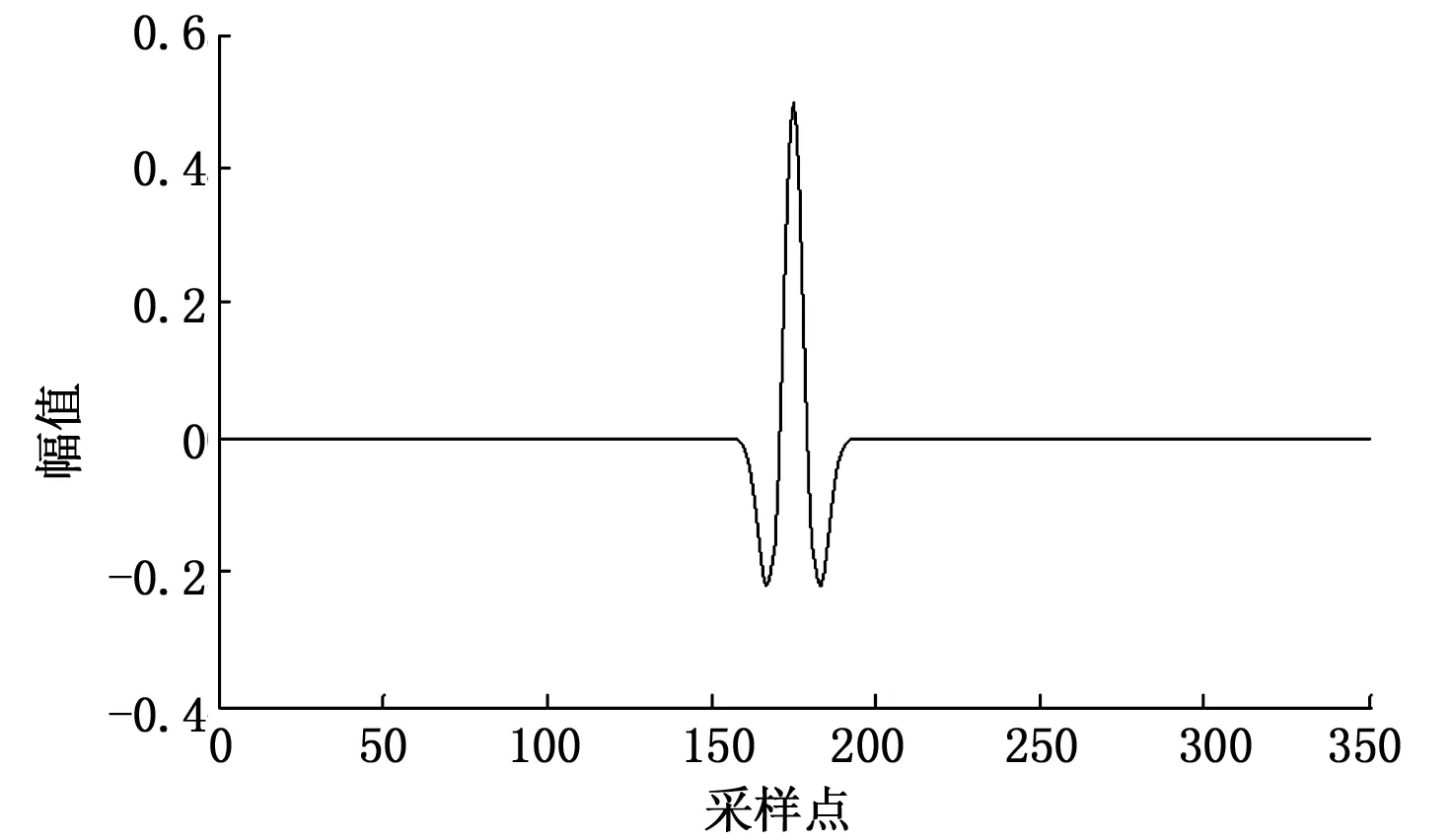
图2 原始信号

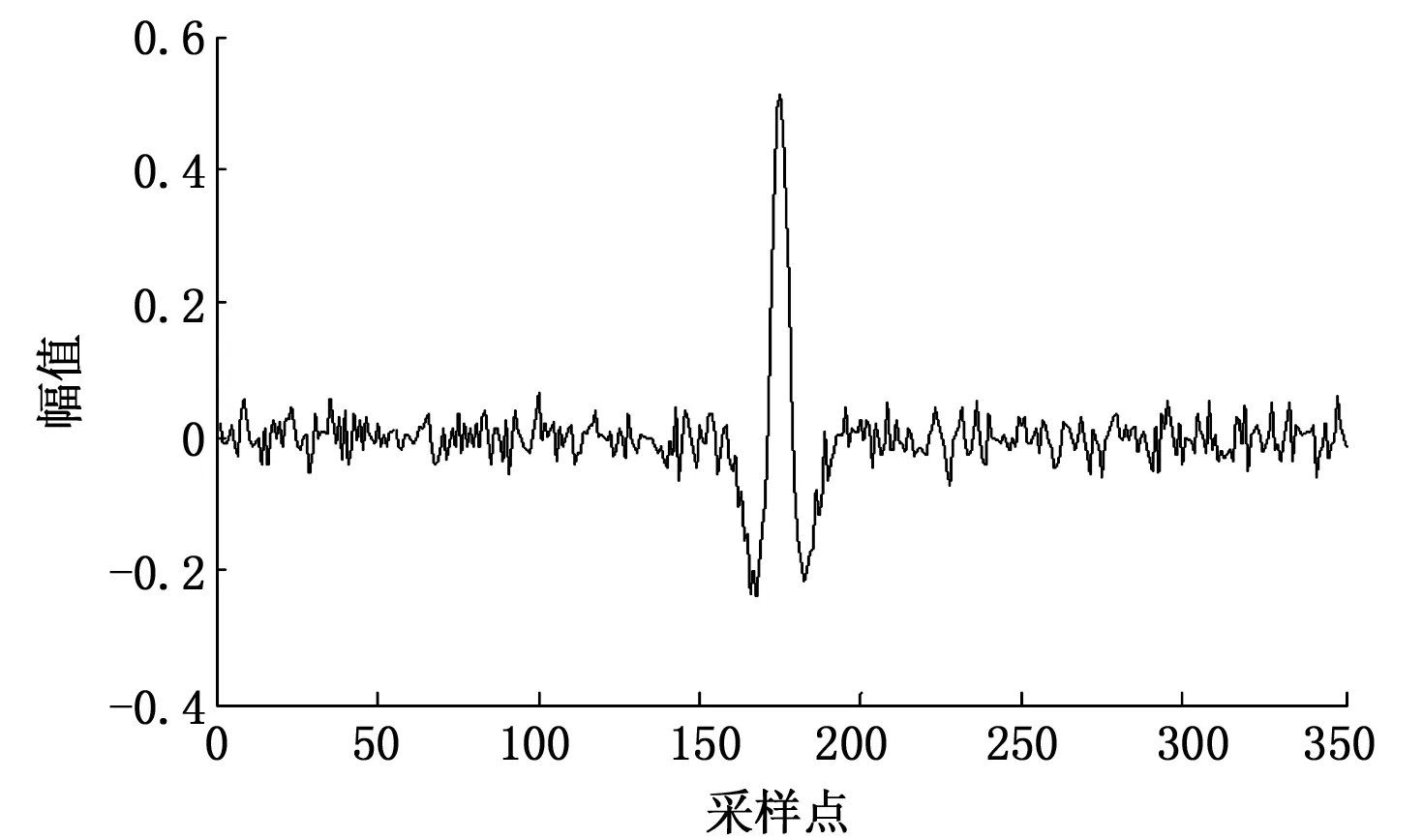
图3 加噪信号

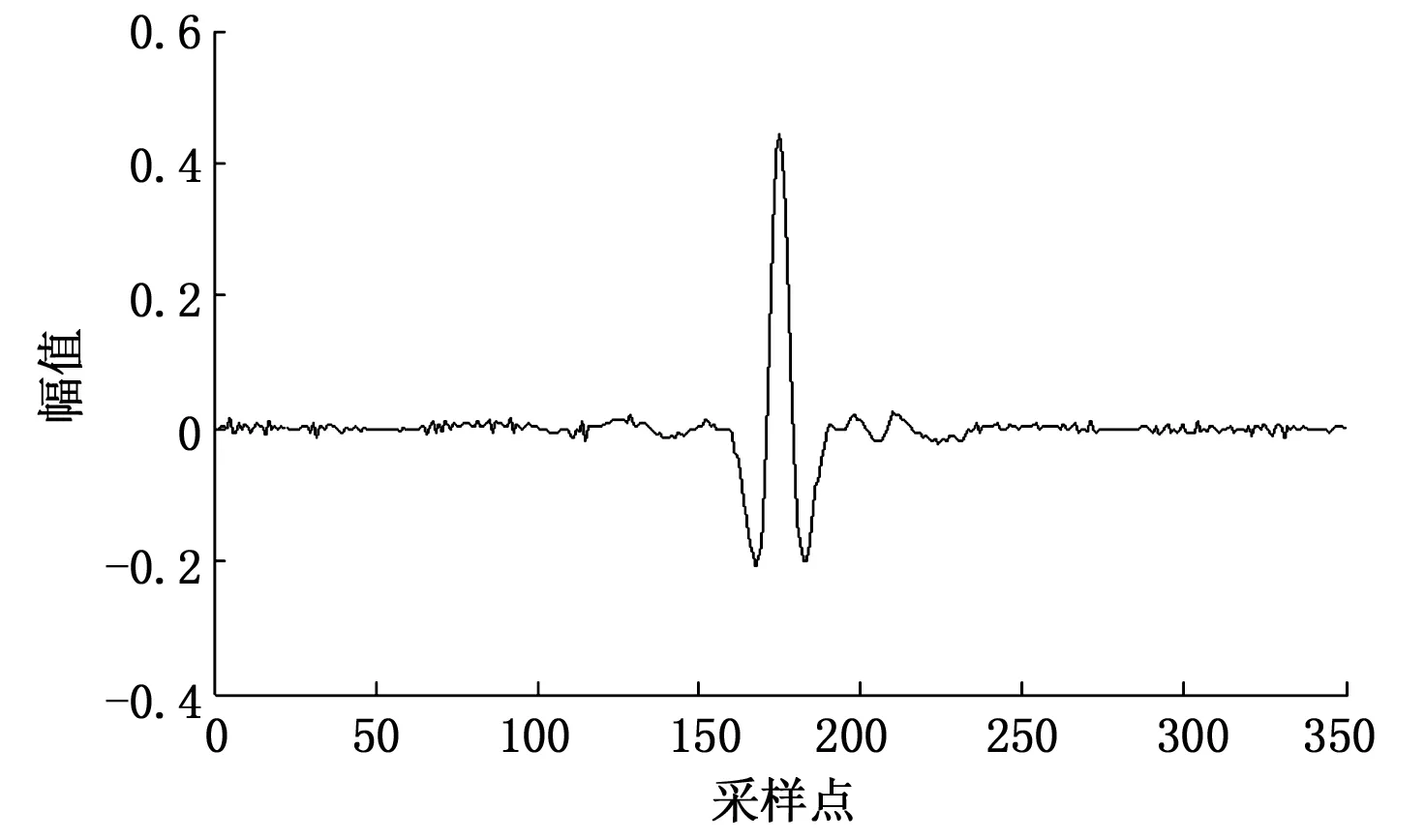
图4 EMD低通去噪后的信号

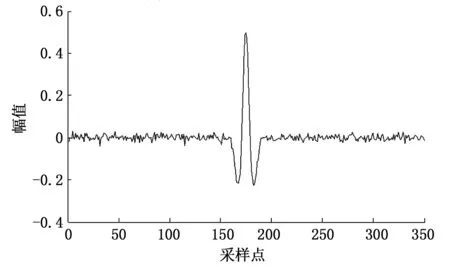
图5 小波去噪后的信号

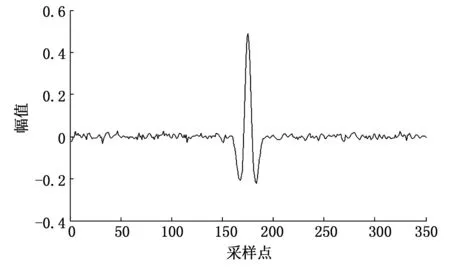
图6 联合去噪后的信号

分别采用EMD低通去噪法、小波阈值去噪和本文所提联合去噪方法对加噪后的信号进行去噪处理，得到如图4～6所示的结果。其中小波函数选取dB5小波，分解层次为5层，小波阈值函数采用软阈值函数，并且阈值确定规则相同。从图2(c)中可以看出，由于噪声主要分布在第一个高频分量中，经EMD低通法去噪后，能够有效的压制噪声，去噪后的信号平滑，几乎无毛刺。但由于高频分量中仍含有有效信息，舍弃高频分量，使得信号在降噪的同时幅值有所降低。

从图5和图6中可以看出，信号经过小波阈值去噪和联合去噪方法去噪后，都能有效地压制噪声，较好恢复信号的原貌，并且本文所提方法去噪后的信号更加平稳，毛刺更少。由此可以直观的看出联合去噪算法的优势。

为定量评估去噪算法的去噪性能，引入均方根值(Root-Mean-Square Error，RMSE)和信噪比(Signal to Noise Ratio, SNR)的概念，公式如下

(8)

(9)

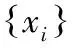
分别按照公式(8)和(9)计算3种算法的RMSE和SNR，所得结果见表1。从表1中能更好地看出3种算法的差异。对比两个指标的性能可以看出，本文所提算法显著的降低了RMSE，相对于小波直接去噪算法，信噪比提升了约6个dB，而相对于EMD低通去噪法提升了8个dB。

表1 3种去噪算法参数对比

3 实测冲击信号分析

为了考核某产品在恶劣环境条件下的生存能力，现开展跌落试验，以模拟实际工作中的冲击环境，分析冲击对产品的破坏程度。本文选取一段跌落试验中的测试数据作为原始信号，从图7中可以看出，背景噪声很强，实测信号受噪声干扰明显。

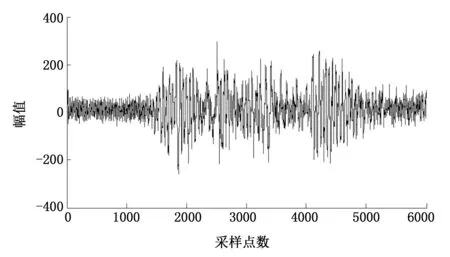
图7 原始含噪信号

3.1 小波阈值去噪

图8所示为直接对冲击信号进行小波降噪的结果，降噪过程选取dB5小波，分解层数为5，采用软阈值去噪方法。从图8中可以看出，直接运用小波阈值去噪的方法基本上可以将信号从噪声中还原，去噪效果比较理想，但是去噪后的信号部分尖点仍然较模糊，信号仍存在较多毛刺。

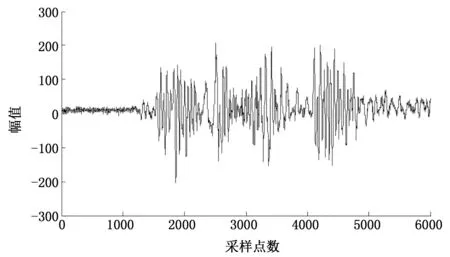
图8 小波阈值去噪后的信号

3.2EMD低通去噪

对冲击信号进行EMD分解，冲击信号分解为imf1～imf11共11个分量和1个残余量res，分量图见图9～10。从图中可以看出噪声主要存在于imf1、imf2和imf3三个分量中。

按照EMD低通滤波去噪方法的原理，将前3个高频分量去除，剩余分量重构的信号见图11。从图11中可以看出，去噪后的信号清晰光滑，噪声被有效去除，但信号幅度明显降低。这是由于被舍弃的前3个分量在含有噪声的同时，也包含有用信息在内。EMD去噪法在去除噪声的同时，高频分量中的有效信息被误作噪声而舍掉。直接EMD去噪的方法在去除高频噪声的同时会削减有用信号，造成信息丢失，因此这种去噪方法是比较粗糙的。图12为EMD低通去噪后的信号差值，从图12中可以看出，信号差值有明显尖峰部分，这也说明部分有用信号被误作噪声，在去噪的同时被舍掉。

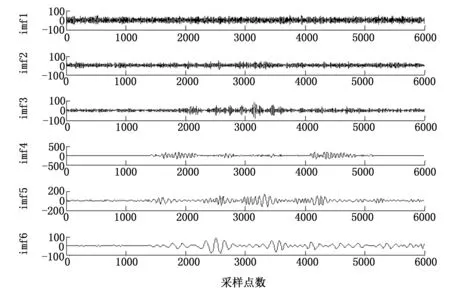
图9 原始信号EMD分解的IMF分量(imf1～imf6)

图10 原始信号EMD分解后的IMF分量及残余量(imf7～imf11、res12)

图11 EMD低通去噪后的信号

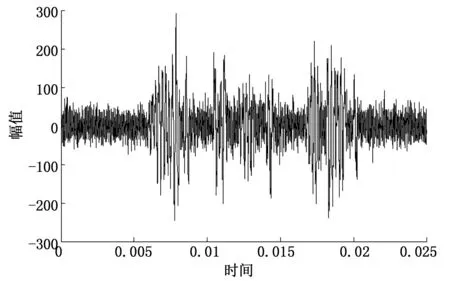
图12 EMD低通去噪后的信号差值

3.3EMD-小波阈值联合去噪

为避免EMD低通去噪法中将高频分量中有用信息误作噪声的弊端，将EMD分解和小波阈值去噪相结合，对含噪的冲击信号进行去噪处理。首先通过连续均方误差准则得出分界点is=3，因此对分量imf1、imf2和imf3进行小波阈值去噪处理，其余分量则不作处理，保持不变。去噪前和去噪后的前3个imf分量见图13～14。将去噪后的3个分量和其余分量相加，得到重构后的信号，即为联合算法去噪后的信号，重构信号见图15。从图15中可以看出，噪声被有效去除，联合去噪后的信号较平缓，基本无毛刺，去噪效果理想。并且从图16中可以看出，与EMD低通滤波相比较，信号的去噪差值平缓，无尖峰，说明去除的基本是噪声，原始冲击信号中的有用信号得以保留。

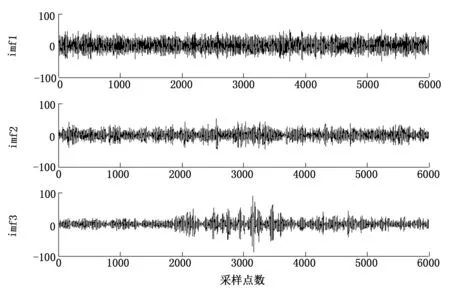
图13 去噪前的前3个imf分量

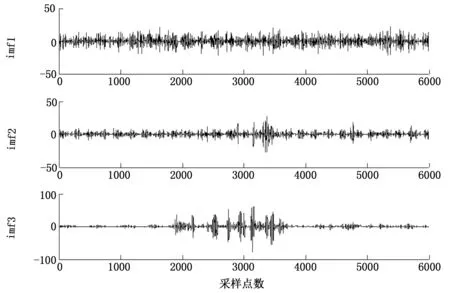
图14 去噪后的前3个imf分量

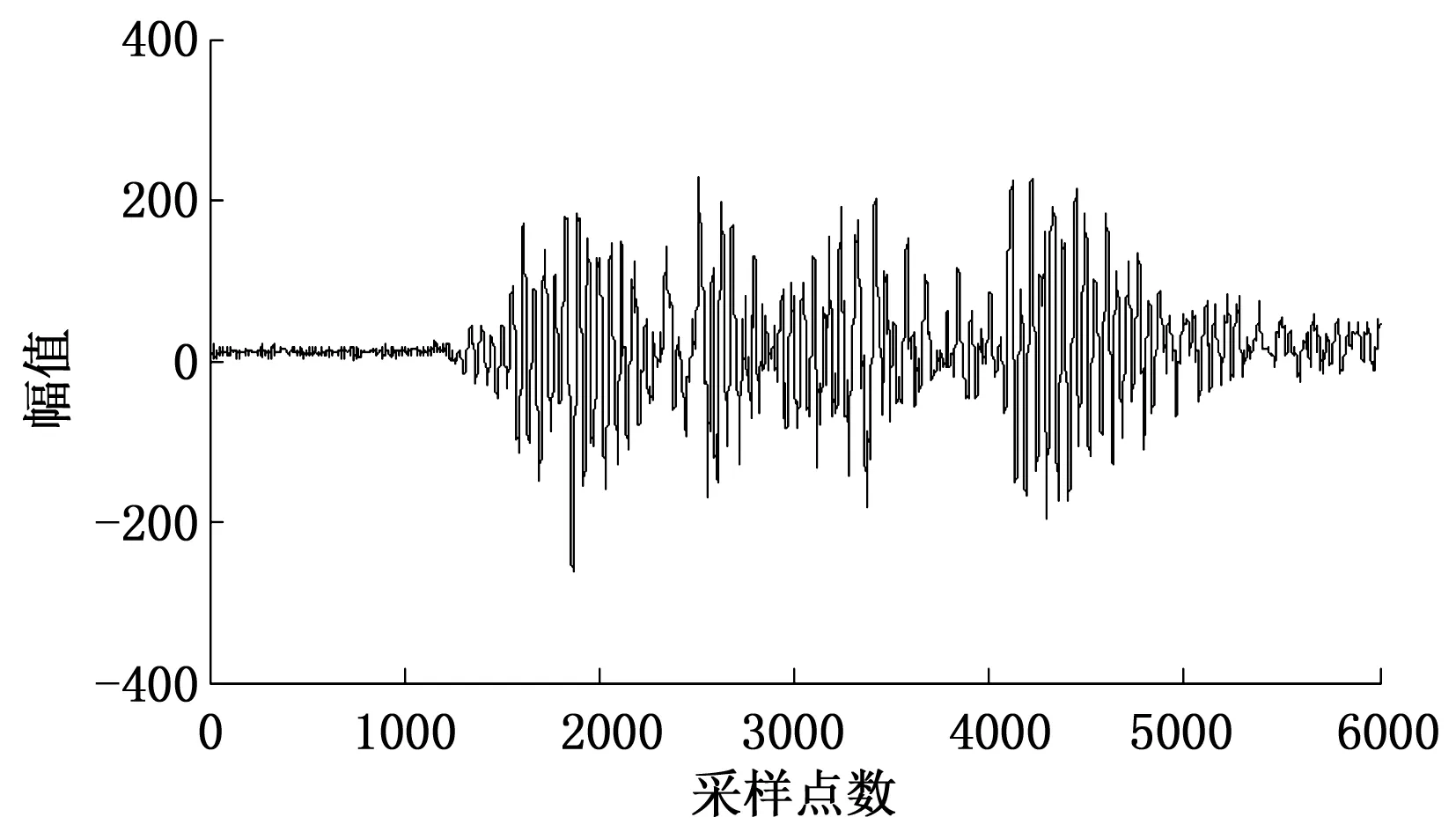
图15 联合去噪后的信号

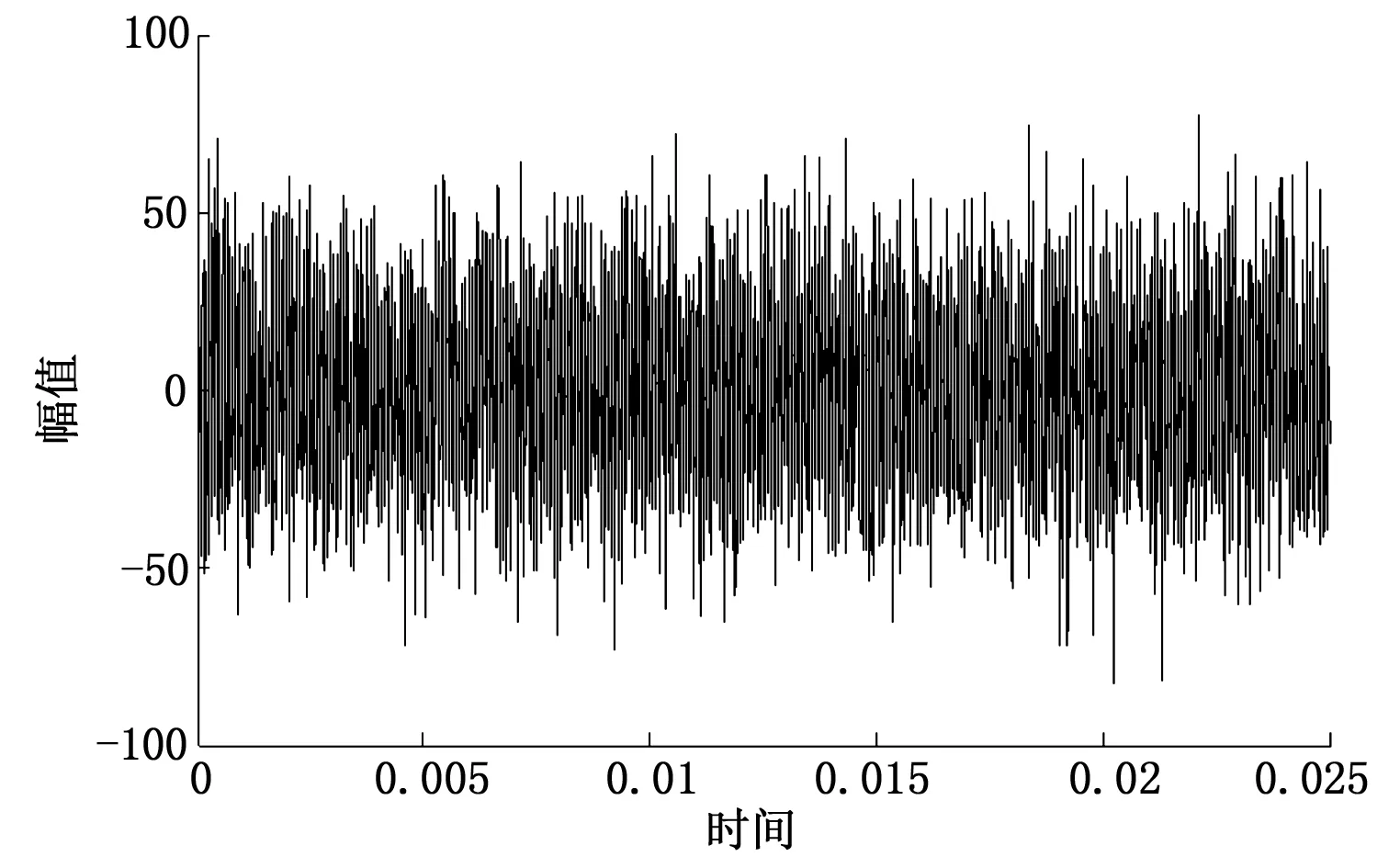
图16 联合去噪后的信号差值

3.4 去噪效果对比

为了对比3种去噪算法的去噪性能，分别对原始信号、EMD低通法、小波阈值法和联合去噪法去噪后的信号做傅里叶变换，得到信号的频谱图，见图17～20。

分析可知:

1)原始信号频率分布散乱，充满整个频率坐标轴，高频部分分量明显。小波阈值法去噪后，信号大于50 kHz的部分，频率幅值大幅减小，但仍有分布；EMD低通滤波法和联合去噪法去噪后，大于50 kHz的部分，频率幅值分布大幅减少，趋近于0。因此，频谱分布说明小波阈值法去噪能力相对有限，而EMD低通去噪法和联合去噪法去噪效果更完全。

2)对比原始信号和去噪后的信号频谱图可知，EMD低通法去噪后信号在低频段的能量明显降低，也即，部分真实信号连同噪声被一起去除，造成信号失真现象。而联合去噪法去噪中的有用特征信息MF1、MF2和MF3被有效提取，并与其他IMF分量重构，从而避免了信号失真。

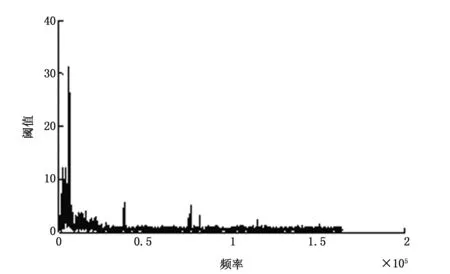
图17 原始冲击信号的频谱图

4 结论

本文针对冲击信号呈现非平稳性以及信噪比低的特点，提出了一种小波阈值降噪和经验模态分解相结合的信号去噪方法。首先对含噪信号进行EMD分解，得到频率由高到低的IMF分量后，利用均方误差准则获得高频与低频的分界点，对高频部分进行小波阈值降噪，并保留低频段的有用信息，使得降噪重构后的信号较好地保留了原始信号的波形特征。本文所提的联合去噪方法兼顾了小波阈值去噪方法和EMD去噪方法的优点，通过仿真可以看出，信噪比和均方根值都有明显改善，证明所提去噪方法可以获得较理想的效果。最后通过对工程冲击信号进行去噪处理，从分析上也可以看出，本文所提方法相较于另外两种方法有较明显的性能提升，从而说明本文所提方法可以应用于实际的冲击信号去噪处理。新的去噪方法简单易实现，为实测冲击信号中的数据去噪和特征信号提取提供了一种较好的解决方法。

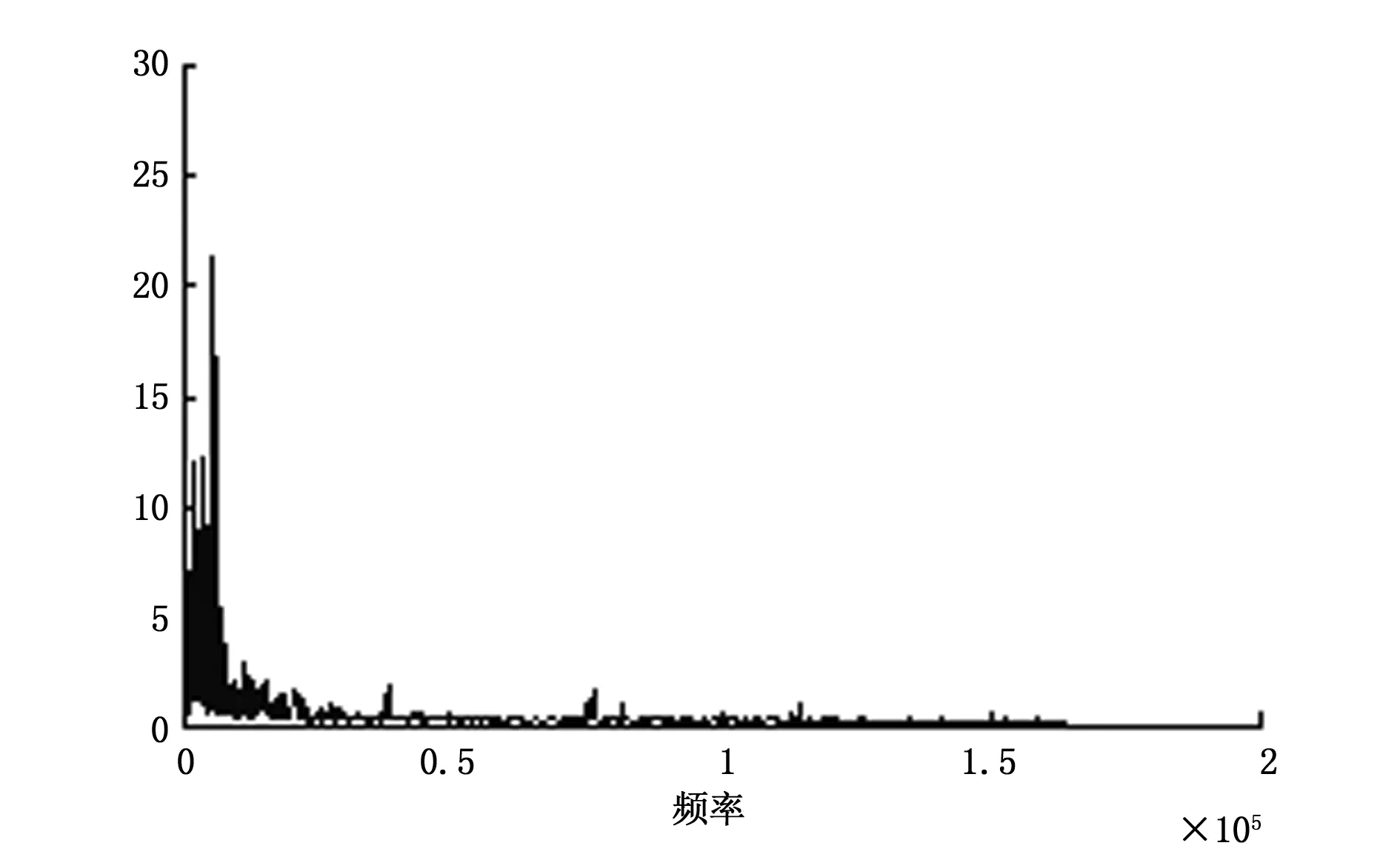
图18 小波阈值去噪后信号频谱图

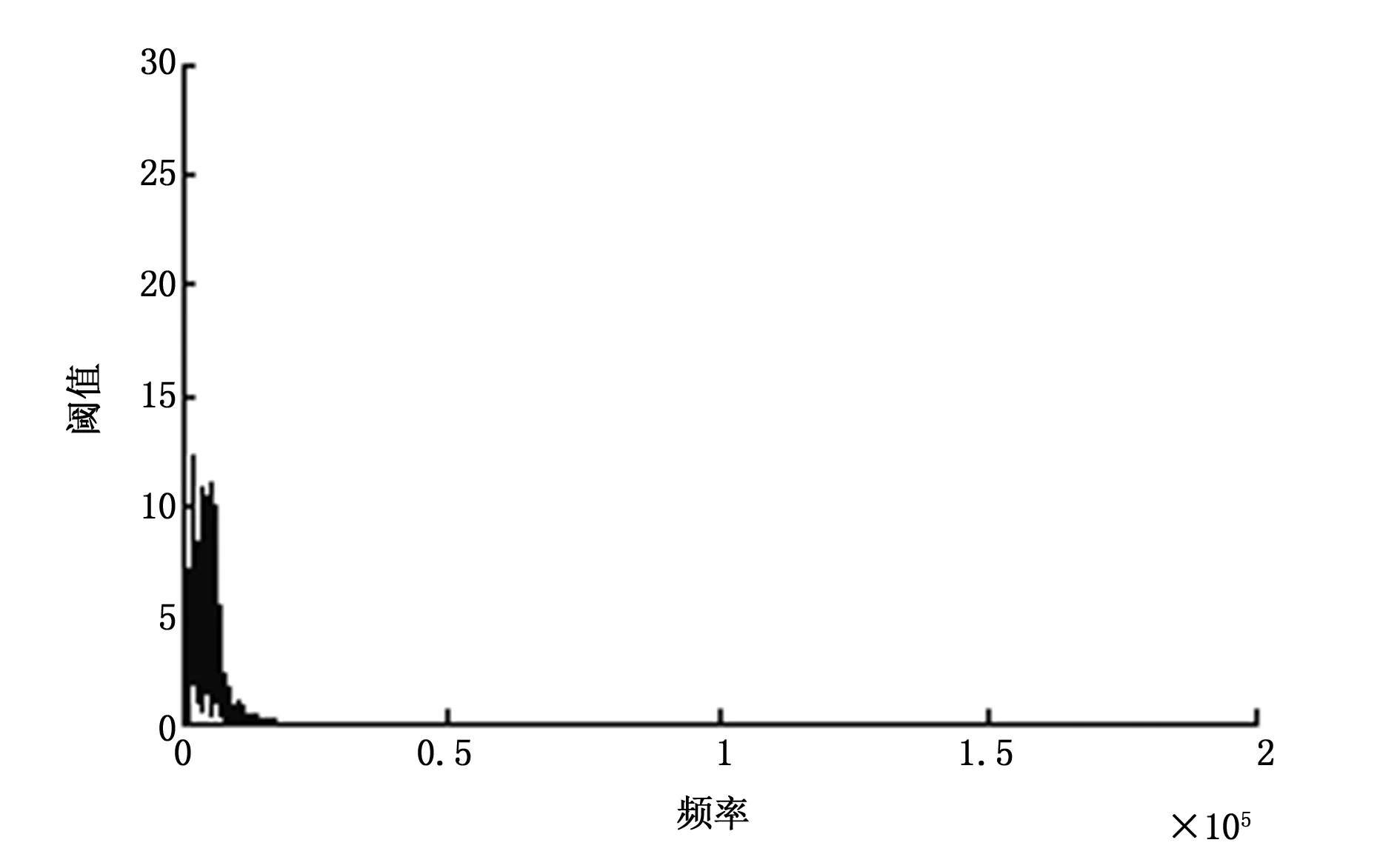
图19 EMD低通去噪后信号频谱图

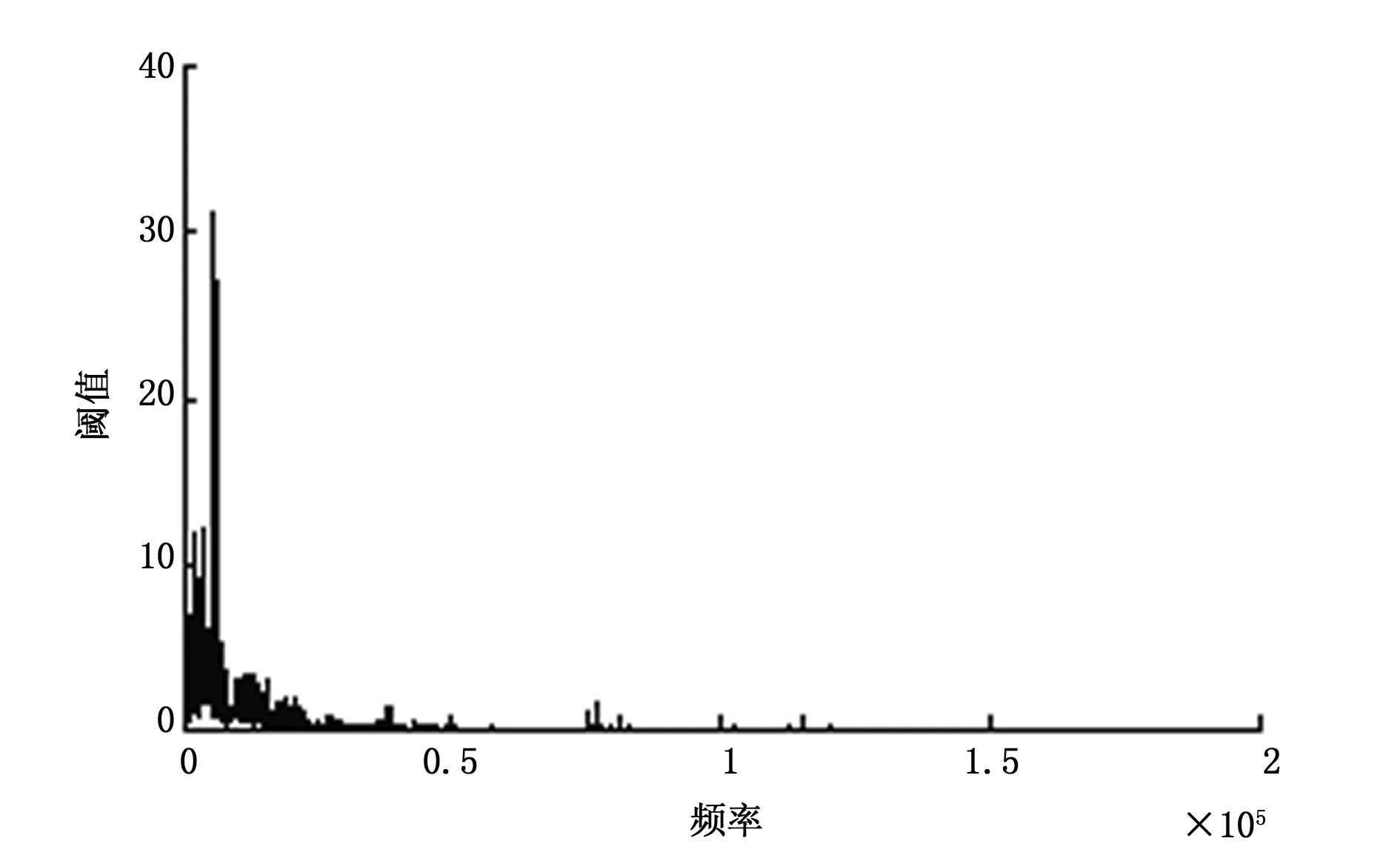
图20 联合去噪后信号频谱图

[1]HuangNE,ShenZ,LongSR,etal.TheempiricalmodedecompositionandtheHilbertspectrumfornonlinearandnon-stationarytimeseriesanalysis[C].ProcRoySocLondA，1998: 903-995.

[2] 王正海，耿 欣，姚卓森，等.基于经验模态分解的MT数据脉冲类电磁噪声处理[J].吉林大学学报：地球科学版，2014，44(1)：344-349.

[3] 梁 喆, 彭苏萍, 郑 晶. 基于EMD和互信息熵的微震信号自适应去噪[J]. 计算机工程与应用,2014，50(4):7-11.

[4]MallatSG.Atheoryformultiresolutionsignaldecomposition:thewaveletrepresentation[J].IEEETrans.Pat.Anal.Mach.Intel, 1989, 11(7): 674-693.

[5] 张 弦, 李世平, 孙浚清, 等. 一种改进的小波阈值去噪方法[J].微计算机信息, 2007, 23(11): 309-311.

[6]WalkerJ.S.APrimeronWaveletsandtheirScientificApplications[M].London.CRCPress, 1999.

[7]PoornachandraS.,Wavelet-baseddenoisingusingsubbanddependentthresholdforECGsignals[J].DigitalSignalProcessing, 2008, 18: 49-55.

[8] 张 通, 张 骏, 张 怡. 基于改进小波阈值的激光陀螺漂移信号降噪[J]. 仪器仪表学, 2011, 32(2): 258-263

[9]HuangNE,ShenZ.TheempiricalmodedecompositionandtheHilbertspecturmfornonlinearandnon-stationarytimeseriesanalysis[Z].

[10]S.Vafaei，H.Rahnejat.Indicatedrepeatablerunoutwithwaveletdecomposition(IRR-WD)foreffectivedeterminationofbearing-inducedvibration[J].JournalofSoundandVibration，2003，260: 67 - 82.

[11]唐进元，陈维涛，陈思雨，等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击，2009，28(7): 118-121.

[12]DonohoDL,JohnstoneIM.Idealspatialadaptationbywaveletshrinkage[J].Biometrika, 1994, 81 (3): 425-455.

[13]DonohoDL.Denoisingbysoft-thresholding[J].IEEETransactionsonInformationTheory, 1995, 41(3): 613-627.

[14]BoudraaAO，CexusJC.EMD-basedsignalfiltering[J].IEEETransactionsonInstrumentationandMeasurement，2007，56(6): 2196-2202.

[15]朱瑞赓，李 铮.爆炸地震波的现场测量及其安全距离[J].爆炸与冲击，1982(1):60-67.

Denoising of Shock Signal Based on EMD and Wavelet Threshold

Su Xiuhong, Li Hao

(Institute of System Engineering, CAEP, Mianyang 621900, China)

Shock signal is easily interfered by noise. As Empirical Mode Decomposition(EMD) denoising method and wavelet threshold denoising method both have their disadvantages, a new denoising method is proposed when they are combined. When removing high-frequency noise, EMD denoising method also suppresses effective high-frequency information. In the proposed denoising method, continuous square error rule is used to define IMF components with higher frequency, and the wavelet threshold method is applied in those components. Meanwhile the other IMF components retains the same. Firstly the performance of proposed denoising method is validated by simulation, then the proposed method is applied in shock signal. The results show that the denoising effect of the proposed method is better than both single methods.

wavelet threshold; EMD; denoising; shock signal

2016-08-03；

2016-09-13。

苏秀红(1988-)，女，硕士，工程师，主要从事动态测试技术与数字信号处理方向的研究。

1671-4598(2017)01-0204-05DOI：10.16526/j.cnki.11-4762/tp

O322;TN

A