基于锤击法的复合材料层合板振动理论及实验模态分析

李菊峰 杨 涛 杜 宇 牛雪娟

(1 天津鼎华检测科技有限公司, 天津 300350)

(2 天津市现代机电装备技术重点实验室, 天津 300387)

·计算材料学·

基于锤击法的复合材料层合板振动理论及实验模态分析

李菊峰1，2杨 涛1，2杜 宇2牛雪娟2

(1 天津鼎华检测科技有限公司, 天津 300350)

(2 天津市现代机电装备技术重点实验室, 天津 300387)

文 摘 基于实验模态分析理论，构建了复合材料层合板的模态实验理论及测试系统。首先制备了150 mm80 mm3.75 mm的碳纤维复合材料层合板，通过DH5922N动态数据采集仪提取了加速度传感器以及力锤所感应到的频响函数及激励信号。将频响函数导入DHDAS动态信号分析系统后获得复合材料层合板一阶及二阶固有频率分别为323.103和656.180 Hz，并测得对应频率下的各测点振型。结果表明，利用本文所提出的实验理论及所用设备可精确提取复合材料层合板的模态信息。

复合材料, 模态测试, 模态振型, 固有频率

0 引言

因为碳纤维复合材料结构的比模量与比强度相对金属材料比较高，热稳定性、耐疲劳性及减震性能好，所以普遍使用在航天航空、汽车、船舶工程、休闲用品等领域[1-2]。在实际应用中，为保证复合材料使用过程中的安全性能，经常需要对其进行损伤检测[3-5]。然而，损伤识别过程中难免会用到复合材料动力学参数，这些参数的提取必须通过精确的模态分析获得。因此，研究一种精确有效的实验模态分析对于复合材料结构的优化以及使用过程中的安全性能有着非常重要的意义。

模态试验主要获取的参数为结构的固有频率、模态振型以及阻尼比。试验获得模态信息的方法有两种,一种是从纯模态中提取，即使结构只按某一阶模态振型振动，不含其他阵型。孟霞等人[6]利用纯模态法对复合材料板架结构进行了模态分析，而试验过程中要想获得纯模态，必须采用多点激振使得激振力与阻尼力平衡，较难把握。因此，本文采用第二种方法，从频响函数中提取。李凤明等人[7]对碳纤维复合材料动力学特性进行了理论分析，ZHANG R. 等人[8]应用频响函数法对复合材料板结构进行了理论模态分析。刘兵山[9]结合振动模态理论对飞机机翼进行了结构设计。

1 试验模态分析理论基础

对于多自由度无阻尼系统，N阶微分方程矩阵可用来描述其动态特性[10]：

(1)

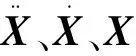
[F]=[F1F2KFn]T

(2)

设公式(1)表示的振动系统的频响函数矩阵为：

(3)

令Xi表示在j点施加单位激振力Fj时i点产生的位移响应，则公式(3)中每项元素Hij可表示为：

Hij=Xi/Fj

(4)

由线性叠加性可知：

(5)

将(5)式进行拉式及傅里叶变换后可得[11]：

(6)

式中,kr、mr表示的是第r阶模态刚度和模态质量，cr、φr则代表构件第r阶的模态阻尼比和模态振型。则由前面定义可知：

(7)

根据公式(7)可知，频响函数矩阵的任意一行为

(8)

可见，频响函数矩阵的任意一行包含了所需的所有模态参数，因此，实验过程中可采用单点拾振的方法测量一行频响函数，计算分析后即可获得所有模态信息。

(9)

同样，频响函数矩阵的任意一列包含了所需的所有模态参数，因此，采用的测试手段为单点激励，多点拾振。

2 实验模态测试

2.1 实验模态分析原理

模态分析是通过一定的变换过程将物理参数计算转化获得模态参数，并构建出模态坐标系[11]。物理参数如相对位移和速度均直接影响弹性力和阻尼力，因此，一般物理系统中的系数矩阵均为非对角矩阵，且向量不正交，而模态坐标中的向量一般是正交的，便于观察结构的物理特性。也就是说结构的运动过程可由模态参数(如固有频率、阻尼比和模态振型位移)等动力学参数来表达。模态试验的目的就是通过振动测试获得结构“模态参数”的。

本文所采用的实验模态分析方法为测力法，也称为频响函数法，是一种经典的模态参数辨识方法。控制理论中的传递函数反映系统的是输入和输出之间的关系，因此，此方法引入了传递函数，反映系统的固有特性，根据传递函数(或频响函数)来识别系统的模态参数。由自带力传感器的力锤敲击构件系统，由传感器(如加速度传感器)测量构件各点的输出响应，后续经过频响函数分析模块计算得到各点模态参数，即如式(9)所示，已知等号左边的频响函数矩阵，可通过分析计算获得等号右边的结构模态参数。

2.2 实验模态分析系统

2.2.1 碳纤维板的制备

试件采用SK化工(青岛)有限公司的TR50碳纤维预浸料铺层后加热固化成型，碳纤维密度为:1.77 g/cm3，树脂的密度为1.2 g/cm3，每层厚度为：0.187 5 mm，共20层，尺寸为150 mm80 mm。

2.2.2 实验设备

(1)仪器的选择

使用DH5922N动态数据采集仪器。DH5922N具有高度集成的模块化设计硬件，每个模块有16、32或64通道机箱形式；每通道具有独立电压放大器以及24位A/D转换器，低通滤波器和抗混滤波器可以消除通道间相互干扰的情况，大大提高了系统的抗干扰能力；仪器使用USB接口与计算机通讯，实时回收信号。满足所有通道同步、并行采集、传输数据；16通道同时工作时，最高采样频率达到256 kHz/通道。

(2)传感器的选择

复合材料板的尺寸较小，选用尺寸小质量轻的传感器，DH132质量只有1 g，频率范围1～2×104Hz，可以选用。力锤选择复合材料专门做复合材料板模态实验的专用力锤。

(3)系统连接示意图

测力法连接示意图如图1所示。

(1)首先在被测物表面选定参考点和测点，选择测点时应当尽量避免模态节点。

(2)将DH132在被测物体表面，安装时注意传感器方向要与测量方向一致。

(3)使用IEPE线连接力传感器和DH5922N数据采集通道，将DH132接DH5857与DH5922N数据采集通道相连，走线时注意线缆接头不受力，不影响被测物振动，注意传感器与测量通道的对应。

(4)使用USB线连接计算机与DH5922N，确保所有连接正确后，打开仪器和软件，连接仪器。

2.3 测量过程

2.3.1 基本流程

采用力锤对试件产生一个激励，在被测物表面选定测点，选择测点时应当尽量避免模态节点，得到传感器的响应，最终得到力锤信号与传感器信号的频率响应，分析后得到试件模态参数。具体实验流程见图2。

2.3.2 实验前的准备

(1)根据建立的模型在试件上划分测点。

(2)选择合适的边界条件安装试件。

(3)按所选的实验方法连接设备。

3 模态分析与结果

3.1 采集与分析

准备完成后，开始采集数据，并通过DHDAS基本分析软件计算出频响函数，如图4所示；将测得的频响函数导入模态软件中进行参数识别，估算出所有模态参数，包括固有频率、模态振型、阻尼比以及模态质量，并依据图5所示进行了识别精确度评价，其中，v代表只有频率、振型稳定，s代表全部稳定。

3.2 模态试验分析结果

长方形复合材料板，激励出了2阶模态。

一阶模态：频率323.103 Hz，阻尼比0.977。

二阶模态：频率656.180 Hz，阻尼比0.615。

图6 一阶模态振型

Fig.6 The first modal shift shapes

4 结论

(1)从振动学理论出发，分析了利用锤击法测试结构模态参数的可行性。被测碳纤维复合材料层合板是采用TR50碳纤维预浸料铺层后加热固化成型的。

(2)实验过程中采用单点激励法进行振动测试，通过传感器获得多个测点的频响函数，分析研究后精确提取出了复合材料层合板一阶及二阶固有频率分别为323.103和656.180 Hz，阻尼比分别为0.977和0.615。并测得对应频率下的各测点振型。

(3)所提出的实验方案以及所用设备可精确测得碳纤维复合材料层合板的模态参数，可以使复合材料结构在远离固有频率下工作，避免共振影响结构正常工作，并且为复合材料损伤检测奠定了基础，通过振型等模态参数的损伤检测方法已经应用于复合材料结构的检测。

[1] 施军, 黄卓. 复合材料结构在海洋船舶中的应用[J]. 玻璃钢/复合材料, 2012(S1):269-273.

[2] 陈新波, 孙金立, 袁英民, 等. 在役航空器上复合材料的综合检测与评价[J]. 无损检测, 2013(7): 50-53.

[3] 王菡, 童明波. 基于定量曲率模态分析的分层损伤检测研究[J]. 航空计算技术, 2012, 42(2): 69-72.

[4] JEONG K S, KWAK Y K. Experimental investigation of the dynamic characteristics of carbon fiber epoxy composite thin beams[J]. Composite Structures, 1995, 33(2): 77-86.

[5] MONTALVAO D, MAIA N M M, RIBEIRO A M R. A review of vibration-based structural health monitoring with special emphasis on composite materials[J]. Shock and Vibration Digest, 2006, 38(4): 295-326.

[6] 孟霞, 李喆, 王德禹. 复合材料板架结构中纯模态试验技术的应用[J]. 噪声与振动控制, 2013(2): 44.

[7] 李凤明, 胡超, 黄文虎. 材料性质对纤维增强复合材料动力学特性的影响[J]. 复合材料学报, 2003(6): 137-141

[8] ZHANG R, NI Q Q, MASUDA A, et al. Vibration characteristics of laminated composite plates with embedded shape memory alloys[J]. Composite Structures, 2006, 74(4): 389-398.

[9] 刘兵山, 燕瑛, 钱卫, 等. 复合材料机翼盒段的设计, 模态分析和试验[J]. 北京航空航天大学学报, 2003, 29(11): 1026-1028.

[10] 梁君, 赵登峰. 模态分析方法综述[J]. 现代制造工程, 2006 (8): 139-141.

Composite Laminates Vibration Theory and Experimental Modal Analysis Based on Hammering Method

LI Jufeng1,2YANG Tao1,2DU Yu2NIU Xuejuan2

(1 Advanced Mechatronics Equipment Technology Tianjin Area Major Laboratory, Tianjin 300387) (2 School of Mechanical Engineering，Tianjin Polytechnic University, Tianjin 300387)

Based on the theory of experimental modal analysis, the modal theory and testing system of composite laminates is established. Firstly, composite laminates of 150 mm80 mm3.75 mm (lengthwidththickness) were built-up. By using DH5922N dynamic data acquisition instrument, the frequency response function and the excitation signal sensed by acceleration sensor and force hammer are obtained. And frequency response function is analysised in the dynamic signal analysis system DHDAS. The first and second natural frequencies were 323.103 Hz and 656.180 Hz respectively, and the shift values of each measurement point corresponding to the frequency were obtained. The experimental results show that the experimental theory and the equipment used in this paper can be used to accurately extract the modal information of composite laminates.

Composite material, Modal testing, Modal shape, Natural frequency

2016-06-13

国家自然科学基金(11372220);天津市高校中青年骨干创新人才培养计划

李菊峰，1990年出生,主要从事复合材料成型技术与装备。E-mail:1220334722@qq.com

杨涛，1970年出生，教授。E-mail:yangtao@tjpu.edu.cn

TB33

10.12044/j.issn.1007-2330.2017.01.005