信息熵和HQ准则在最大Lyapunov指数计算中的应用
2017-02-15杨琪斌刘树勇位秀雷
王 基, 杨琪斌,2, 刘树勇, 位秀雷
(1.海军工程大学 动力工程学院,武汉 430033; 2.国家海洋技术中心漳州基地筹建办公室,北京 100018)
信息熵和HQ准则在最大Lyapunov指数计算中的应用
王 基1, 杨琪斌1,2, 刘树勇1, 位秀雷1
(1.海军工程大学 动力工程学院,武汉 430033; 2.国家海洋技术中心漳州基地筹建办公室,北京 100018)
最大Lyapunov指数是判断时间序列是否为混沌的一个重要判据,目前应用比较广泛的是小数据量法。将信息熵和HQ准则应用在最大Lyapunov指数的算法中,改进了小数据量法。信息熵优化了相空间重构参数,克服了独立求解重构参数的不足;利用HQ准则确定邻近点个数增加了计算时的精度。仿真实验表明该改进的小数据量法在计算最大Lyapunov时具有良好的准确性,对噪声具有良好的鲁棒性。
信息熵;HQ准则;小数据量法;Lyapunov指数
混沌已经应用于许多领域,想要利用混沌,必须要对系统进行混沌识别。一般来说,一个动力学系统的最大Lyapunov指数大于零时,系统处于混沌状态[1]。求得实测时间序列的Lyapunov指数对于故障信号实时诊断具有重要的意义。在Lyapunov指数的计算过程中,存在很多问题,比如计算复杂、计算精度不够高、无法得到实测时间序列的动力学系统的数学表达式等。WOLF等[2]提出的轨道跟踪法具有开创性的意义。为后续的各种算法的出现打下了坚实的基础。但是轨道跟踪法由于容易受到参数的影响,计算精确度比较差。ROSENSTEIN等[3]在Wolf方法基础上,提出了计算最大Lyapunov指数的小数据量法。小数据量法改善了计算精度,但是在参数的选取上仍然存在诸多不足。蒋爱华等[4]使用了改进的互信息法计算时间延迟,提高了计算最大Lyapunov指数的速度。杨爱波等[5]在利用小数据量法计算最大Lyapunov指数时,使用空间栅格法选取最近邻点,大大提高了计算速度,但是对于噪声鲁棒性不佳。刘树勇等[6]在邻近点搜索时应用了kd树算法,提高了邻近点搜索效率,加快了计算速度。杨永锋等[7]使用加权平均计算平均周期,并用最大无波动区间作为计算最大Lyapunov指数的拟合区域,具有便捷性,易于实现。李彬彬[8]将若干最优的时间延迟点对应的最大Lyapunov值求均值,过程简单,但是误差较大。在所有的算法当中,小数据量法由于可以实现对于不完全数据的计算,使用的最多。但是在确定相空间重构的参数和邻近点这两个重要的环节上还有许多的不足亟待解决。例如确定重构参数时缺少整体性,邻近点个数主要是靠经验主观确定等。
在有关算法中,主要采用TAKENS[9]的嵌入定理进行相空间重构,目前对嵌入维数m和时间延迟τ这两个参数的选取主要是把嵌入维数和时间延迟分别单独求解,但是这种方法因为不能够很好的保持原动力系统整体的特性,所以确定的相空间并不一定最佳。本文提出一种新的相空间重构方法,此方法采用信息熵模型来确定嵌入维数m和时间延迟τ,用遗传算法对建立在高维空间的信息熵模型进行求解,从而实现了对重要的重构参数的优化。这种方法不仅保证了两个重构参数的相互联系性,扩充了两个重构参数的整体性关系,还可以在重构之后保持原有的动力学关系。邻近点的个数的选取:邻近点数量太少会导致计算精度差;数量太多则会使计算变得繁琐。在计算中通常使用最多的是固定邻近点个数法和固定邻域半径法,但是它们都存在着明显的不足,缺乏足够的说服力。本文利用HQ(Hannan-Quinn)准则[10]来实现邻近点个数的选取,避免了引入质量差的邻近点和伪邻近点引起的不利影响,有效增加了计算精度。
1 基于信息熵的相空间重构
1.1 m和τ的信息熵模型
设定两个变量为X={x1,x2,…,xn}和Y={y1,y2,…,yn},变量的先验概率为{p(xi)}i=1,2,…,n和{p(yi)}i=1,2,…,k,可将信息熵定义:
(1)
此定义描述了变量X的不定性。
类似地,联合熵定义为:
(2)
式中:p(xi,yi)是联合概率。
(3)
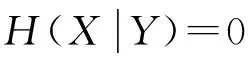

(4)
1.2 相空间重构的参数模型建立
设混沌时间序列为x(1),x(2),…,x(n),…,则一定有合适的嵌入维数m和时间延迟τ的相空间X(n)=(x(n),x(n+τ),…,x(n+(m-1)τ))∈Rm,(n=1,2,…),使得重构相空间与原混沌系统具有等价关系。即存在一个映射F:Rm→Rm能将原混沌系统复原出来,相空间点的轨迹表达式
X(n+τ)=F(X(n)),n=1,2,…
(5)
其中X(n+τ)=(x(n+τ),x(n+2τ),…,x(n+mτ))
式(5)的分量形式为
x(n+jτ)=fj(x(n),x(n+τ),…,x(n+(j-1)τ)),
j=1,2,…,m,n=1,2,…
(6)
将式(6)进行化简后为
x(n+mτ)=f(x(n),x(n+τ),…,
x(n+(m-1)τ)),n=1,2,…
(7)
混沌系统的复杂性导致很难直接得到f的解析式;混沌系统高度的非线性则导致无法确定时间序列未来某时刻的值。
由式(7)可得,在选取合适的嵌入维数m和时间延迟τ下,f可以反映原系统运动模式。首先,得出f中m和τ具有的一般熵关系;其次,用神经网络逼近f。
式(7)还说明了,在知道x(n),x(n+τ),…,x(n+(m-1)τ)后能够确定x(n+mτ),即只有在知道m个时刻的值x(n),x(n+τ),…,x(n+(m-1)τ)后,才可以彻底消除未来某时刻x(n+mτ)的不定性。故嵌入维数m和延迟时间τ是必须紧密联系才能消除未来值的不确定性。信息熵能够刻画不定性,所以m和τ的熵关系可以建立。记
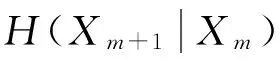
由以上讨论,得到求m和τ的优化模型:
目标函数
(8)
约束条件:m和τ为非负整数。
根据式(4),条件熵变换成联合熵为:
minH(m,τ)=
H(X1,X2,…,Xm,Xm+1)-H(X1,…,Xm)
(9)
1.3 求解相空间重构参数的信息熵模型
式(8)的目标函数中的熵函数是一个有关m和τ的表达式,虽然利用传统的优化算法可以求解式(8),但是由于这个熵函数非常复杂,使用传统算法的可操作性不高,所以采用遗传算法进行求解。
遗传算法(GA)是一种非数值优化算法,使用它求解优化问题只需目标函数就可以进行优化问题求解,并且没有传统的优化算法的缺点。
遗传算法求解的算法如下:
1)编码:参数m和τ为非负整数,采用二进制编码。
2)初始群体的确定:参照实际问题反复试验随机产生群体规模为Q[30,80]。
4)选择算子:使用比例选择算子。即个体在下一代群体中的个数由该个体的适应值在种群总的适应值中的比例来决定。
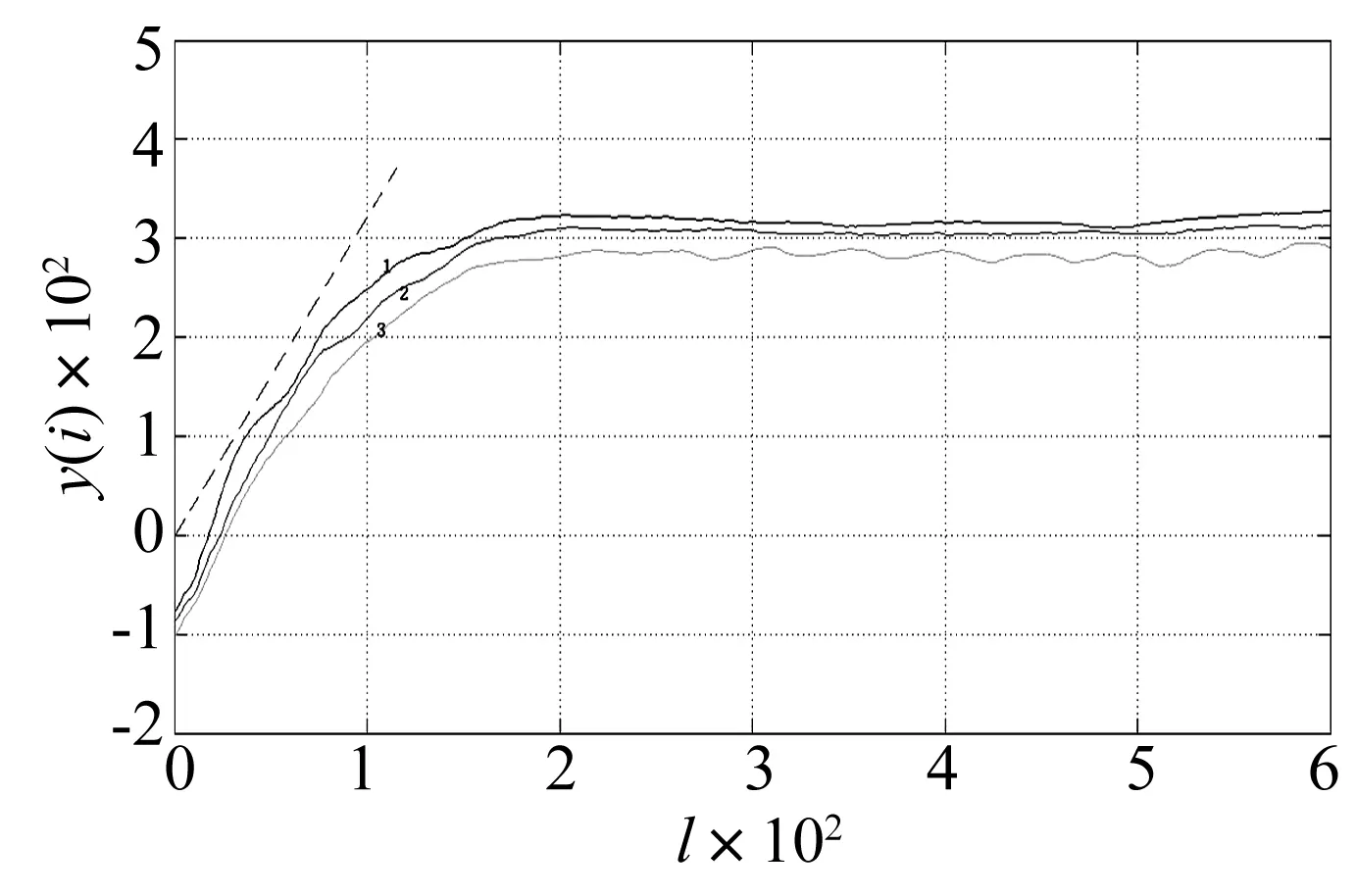
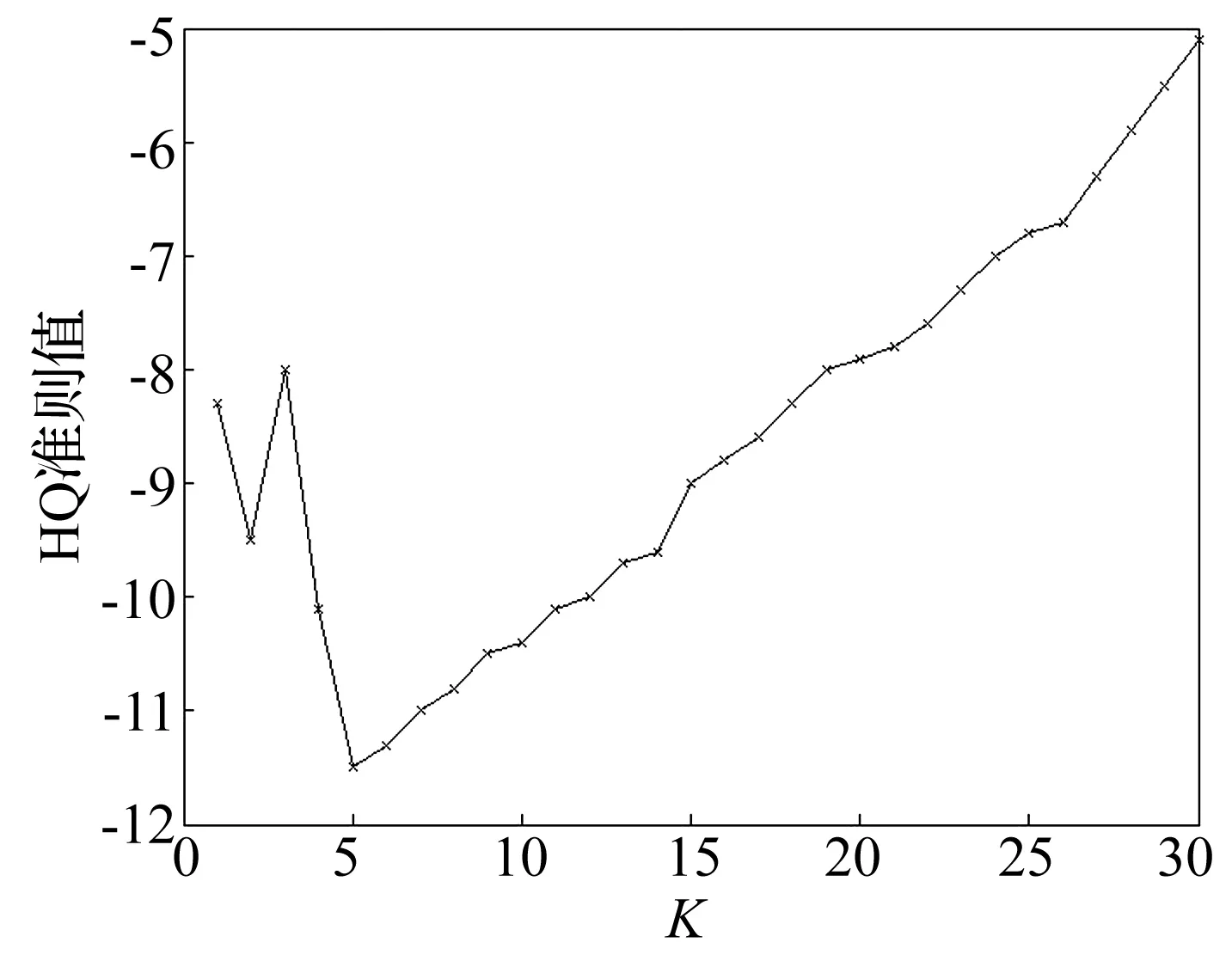
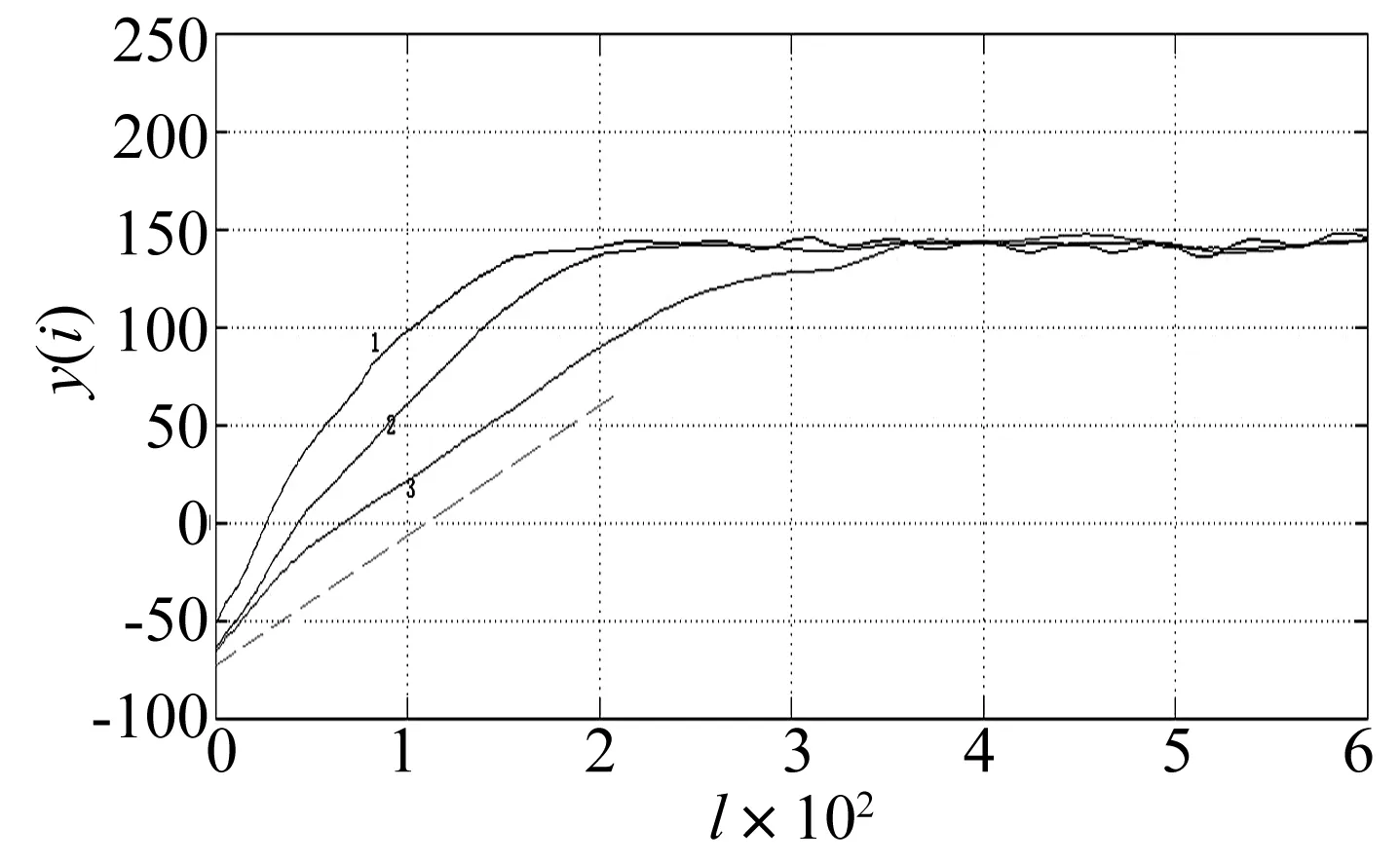
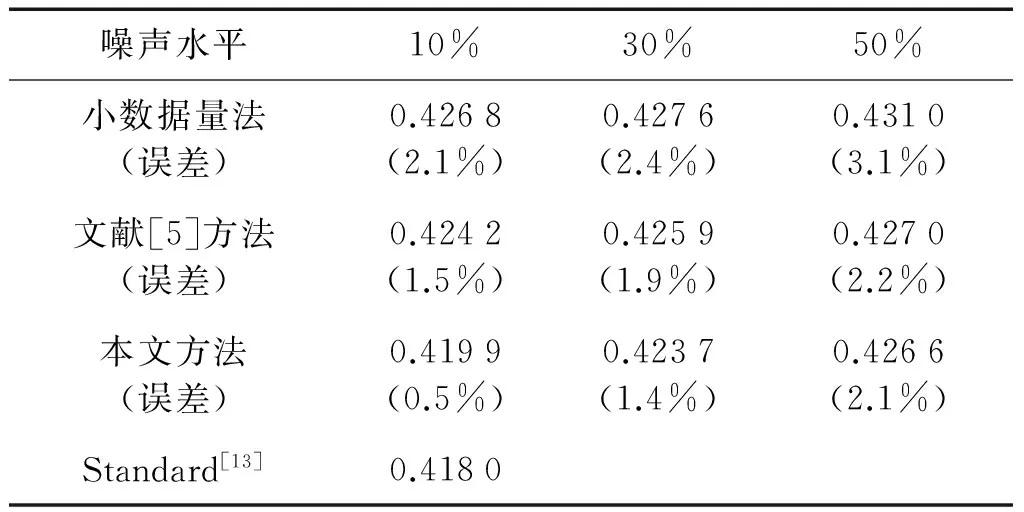
5)交叉算子:使用两点交叉算子。交叉概率pc为0.7 6)变异算子:使用基本位变异算子。变异概率pm:0.01 7)终止条件:最大迭代次数T<100。 邻近点的个数是混沌特征指数计算过程中的另一个重要参数,如何确定最优个数值得研究。本文利用HQ准则[10]来计算得到最优邻近点个数值。 经过研究发现,对于建立拟合模型,需要考虑模型的复杂度和拟合效果。充足数量的模型参数可以保证拟合精度;参数过多则使复杂度增大,甚至导致过拟合现象的发生。 赤池弘次提出赤池信息准则,简称AIC准则[11-12],用于确定ARMA(p,q)模型的独立参数个数: AIC(p,q)=lnσ2+2(p+q+1)/N (10) 式中:σ2是拟合方差,N是拟合数据个数。AIC准则的意义在于平衡模型的拟合精度和复杂度。但AIC准则仍存在着一定的局限性。 HANNAN等对赤池弘次的AIC准则进行了完善和优化,然后提出了HQ准则[10](Hannan-Quinn定阶准则): (11) 式中:D是表征权重的常数,取D>2;σ2需要根据不同的需要对具体定义进行修改。拟合模型的精度和复杂度之间的最佳平衡点是式(11)取得最小值时。 先对邻近点个数K设定一个比较大的取值范围K∈[Kmin,Kmax]。分别对每个K值对应的HQ准则值进行计算,公式如下: (12) 得到一系列准则值后,式(12)的最小值对应的K值就是邻近点个数的最优选择。 其中,归一化均方误差: σ2= (13) 为了检验本文中基于信息熵和HQ准则改进的小数据量法在计算Lyapunov指数时的准确性和对噪声的鲁棒性,分别对Lorenz系统和含噪声的Henon系统的最大Lyapunov指数采用不同的方法进行计算。 (1)Lorenz系统 Lorenz方程 (14) 式中:σ=10,r=28,b=8/3,令x(0)=1,y(0)=0,z(0)=1。采用四阶Runge-Kutta法对Lorenz方程进行求解,取步长为0.02,得到x的7 500个点的数据集,去除暂态过程的前面5 000个点,最后得变量x的一个2 500个点的时间序列,并将其归一化到[0,1]区间,原始数据选前2 000个点。 通过第2节所介绍的方法得到的最优嵌入参数:m=9,τ=4。 通过第3节中所介绍方法,得到每一个K值对应的HQ准则值,见图1。 图1 HQ准则值与K值的关系Fig.1the relationship of HQ values and K values based on HQ rules 从图1看出当K=11时,HQ准则值最小,因此最佳邻近点个数可取为11。 图2中横坐标为演化步数,纵坐标为演化距离,虚线斜率为最大Lyapunov指数的理论值。图中曲线1,2,3分别为本文方法、文献[5]方法和小数量法的演化曲线。采用不同方法计算Lorenz系统的最大Lyapunov指数和误差,如表1。从表中可以看出,采用本文算法计算最大Lyapunov指数,准确性最高。 图2 演化曲线图Fig.2 Evolution curve 方法LE误差小数据量法2.89776.8文献[5]方法2.90326.6本文方法3.03732.3Standard[13]3.1096 (2)含噪声的Henon系统 Henon映射: (15) 式中:a=1.4,b=0.3。令y1=y2=0.5,求得混沌时间序列,去除前面2 000个点,取后边2 000点。 通过第2节中所介绍的方法得到的最优嵌入参数:m=2,τ=1。 通过第3节中所介绍方法,得到每一个K值对应的HQ准则值,见图3。 图3 HQ准则值与K值的关系Fig.3 The relationship of HQ values and K values 从图3看出当K=5时,HQ准则值最小,因此最佳邻近点个数可取为5。 图4是10%噪声水平下演化图的局部放大图。横坐标为演化步数, 纵坐标为演化距离,虚线斜率为最大Lyapunov指数的理论值。图中曲线1,2,3分别为本文方法、文献[6]方法和小数据量法的演化曲线。 图4 演化曲线图Fig.4 Evolution curve 分别向Henon系统中加入10%、30%和50%的噪声,采用不同的方法计算不同噪声水平下Henon时间序列的最大Lyapunov指数和误差,如表2。仿真结果表明,计算精度随着噪声水平的增大而降低。但是本文方法可以计算含噪声的Henon时间序列的最大Lyapunov指数,并且计算准确度比其它方法高,说明该方法对噪声具有很好的鲁棒性。 表2 不同方法计算最大Lyapunov指数的对比 本文利用信息熵和HQ准则对小数据量法进行改进,用来计算混沌序列最大Lyapunov指数。利用信息熵来确定相空间重构的参数,保证了两个重构参数之间的相互联系,扩充了两个重构参数的整体性关系,实现了对重构参数的优化求解,还可以在重构之后保持原有的动力学关系;利用HQ准则来确定邻近点的个数,可以消除引入质量差的邻近点和伪邻近点对计算的不利影响,增加了计算准确性。仿真实验的结果表明,将信息熵和HQ准则应用于小数据量法来计算最大Lyapunov指数是可行的,并且具有良好的准确性;对混沌系统加入噪声之后算出的Lyapunov指数准确度仍然很高,说明本文方法对噪声具有良好的鲁棒性。 [ 1 ] GENCAY R,DECHERT DAVIS W. An algorithm for the n-dimensional unknown dynamical system [J]. Physica D,1992,59:142-157. [ 2 ] WOLF A,SWIFT J B,SWINNEY H L,et al. Determining Lyapunov exponents from a time series [J]. Physica D,1985,16:285-317. [ 3 ] ROSENSTEIN M T ,COLLINS J J, DE LUCA C J. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D,1993,65:117-134. [ 4 ] 蒋爱华,周璞,章艺,等.相空间重构延迟时间互信息改进算法研究[J].振动与冲击,2015,14(2):71-74. JIANG Aihua,ZHOU Pu,ZHANG Yi. Improved mutual information algorithm for phase space reconstruction[J]. Journal of Vibration and Shock,2015,14(2):71-74. [ 5 ] 杨爱波,王基,刘树勇,等.基于空间栅格法的最大Lyapunov指数算法研究[J].电子学报,2012,40(9):1871-1875. YANG Aibo,WANG Ji,LIU Shuyong,et al. An algorithm for computing the largest Lyapunov exponent based on space grid method[J]. Acta Electronica Sinica,2012,40(9) :1871-1875. [ 6 ] 刘树勇,杨庆超,位秀雷,等.邻近点快速搜索方法在混沌识别中的应用[J].华中科技大学学报(自然科学版),2012,40(11):89-92. LIU Shuyong,YANG Qingchao,WEI Xiulei,et al.The application of fast searching nearest points methodto chaos identification[J].J.Huazhong Univ. of Sci.&Tech.(Natural Science Edition),2012,40(11):89-92. [ 7 ] 杨永锋,仵敏娟,高喆,等.小数据量法计算最大Lyapunov指数的参数选择[J].振动、测试与诊断,2012,32(3):371-374. YANG Yongfeng, WU Minjuan, GAO Zhe,et al. Parameter selection of maximum Lyapunov exponent for small data volume method[J]. Journal of Vibration,Measurement & Diagnosis,2012,32(3):371-374. [ 8 ] 李彬彬.非线性心音时间序列的最大Lyapunov指数[J]. 上海电机学院学报,2011,14(1):17-20. LI Binbin. Largest lyapunov exponents of nonlinear heartbeat time series[J]. Journal of Shanghai Dianji University,2011,14(1):17-20. [ 9 ] TAKENS F. Dynamical systems and turbulence[M].Berlin:SpringVerlag,1981,366. [10] HANNAN E J,QUINN B G.The determination of the order of an autoregression [J].Journal of the Royal Statistical Society SeriesB(Methodological),1979:190-195. [11] AKAIKE H. Autoregressive model fitting for control [J]. Annals of the Institute of Statistical Mathematics,1971,23(1): 163-180. [12] AKAIKE H. A new look at the statistical model identification [J]. Automatic Control,IEEE Transactions on,1974,19(6):716-723. [13] GAO Jianbo,ZHENG Zheming. Local exponential divergence plot and optimal embedding of a chaotic time series[J]. Physics Letters A,1993(181):153-158. Application of information entropy and HQ rule in estimating largest Lyapunov exponent WANG Ji1, YANG Qibin1,2, LIU Shuyong1, WEI Xiulei1 (1. College of Power Engineering,Naval Uniwersity of Engineering,Wuhan 430033,China;2. The Zhangzhou Base Preparation Office of National Ocean Technology Center, Beijing 100018, China) The largest Lyapunov exponent is an essential criterion to judge if a time series is chaos or not. The small-data method is widely used in chaotic characteristic extraction at present. Here, the information entropy and HQ rule were applied in estimating the largest Lyapunov exponent to improve the small-data method. The information entropy was applied to optimize parameters of phase space reconstruction, and disadvantages of traditional algorithms were overcome clearly. The computational accuracy of LE was improved greatly by using the HQ rule to calculate the number of neighbouring points. Simulation results showed that the improved small-data method here has good performances in estimating the largest Lyapunov exponent, and the algorithm is robust to noise. information entropy;HQ rule;small-data method;lyapunov exponent (LE) 国家自然科学基金(51179197);海洋工程国家重点实验室(上海交通大学)开放课题(1009) 2015-08-17 修改稿收到日期:2016-01-03 王基 男,副教授,1964年6月生 杨琪斌 男,助理工程师,1991年8月生 O322 A 10.13465/j.cnki.jvs.2017.01.0192 邻近点个数的选择
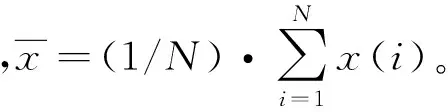
3 仿真实验


4 结 论
