参数激励驱动微陀螺系统的非线性振动特性研究

尚慧琳， 张 涛， 文永蓬

(1. 上海应用技术大学 机械工程学院，上海 201418； 2. 上海工程技术大学 城市轨道交通学院，上海 201620)

参数激励驱动微陀螺系统的非线性振动特性研究

尚慧琳1， 张 涛1， 文永蓬2

(1. 上海应用技术大学 机械工程学院，上海 201418； 2. 上海工程技术大学 城市轨道交通学院，上海 201620)

对于一类典型的切向梳齿驱动型微陀螺,建立两自由度、具有刚度立方非线性和参数激励驱动的微陀螺系统动力学模型。考虑主参数共振和1∶1内共振的情况，利用多尺度法获得周期解的解析形式，并利用分岔理论，得到Hopf分岔条件，结合数值模拟系统的动力学响应，揭示系统参数对驱动和检测模态振幅和分岔行为的影响机制。研究结果表明，在1∶1内共振和较大的载体角速度下，激励频率的变化容易引起微陀螺振动系统的多稳态解、振幅跳跃现象和概周期响应等复杂动力学行为。

微陀螺；静电力；主参数共振；多稳态现象；振幅跳跃现象

静电驱动微陀螺是建立在微纳米技术基础上的静电微惯性传感器，是微机电系统(MEMS)的重要器件, 也是目前发展最快的MEMS产品之一[1-2]。其功能是测量运动物体的旋转速度或旋转角以应用于惯性导航，驱动和检测方式分别为MEMS领域广泛采用的静电驱动和电容检测，具有广泛的应用前景[3]。

从20世纪80 年代后期开始，全世界各国相继开展了对静电驱动微陀螺的研究，热点集中在微陀螺的稳定性和高精度方向[4-5]。早期采用的静电驱动微陀螺动力学模型为集总参数系统模型，即两自由度线性振动系统模型，考虑线性阻尼和刚度，以及简谐激励静电力，通过直接求解线性常微分方程研究微陀螺振动特性。然而，微尺度效应使得静电驱动微陀螺出现了许多宏观机械结构不具备的新的物理现象和特征，如力的非线性(静电力[6-8]、弹性力和粘性力)，阻尼和刚度非线性、以及多场耦合等因素[9]。在设计中采用忽略这些非线性因素的系统模型，容易因无法准确描述微惯性传感器的振动特性而造成微陀螺检测的不准确[10]。为此，越来越多的国内外学者开始关注微陀螺的建模和非线性振动特性研究[11-16]。罗跃生[11]考虑静电吸引力和干扰力对硅微型梳状线振动驱动式陀螺仪建立了活动质量中心在动系中运动的两自由度微分方程模型。KENIG等[12]考虑刚度非线性和参数激励静电力，建立了微陀螺两自由度振动系统，数值模拟发现系统存在高维混沌。FRANCESCO等[13]针对一类音叉振动式微机械陀螺的振动模态建立了具有非线性压膜阻尼，立方非线性刚度的单自由度振动系统，通过数值仿真和实验研究发现随着驱动电压的变化，驱动模态会发生概周期振动和多稳态现象。李欣业等[14]建立了简谐激励静电力、驱动和检测方向均具有三次刚度非线性的微陀螺系统，分析了主共振解的稳定性,数值模拟发现系统存在多稳态现象，并提出利用时滞反馈的方法来抑制系统Hopf分岔。盛平等[15]针对一类梳齿驱动型微陀螺建立了具有三次刚度非线性和参数激励静电力的单自由度驱动模态振动系统模型，发现梳齿电容非线性因素会造成谐振频率的漂移。文永蓬等[16]研究驱动和检测微弹性梁的非线性刚度对微陀螺输出的影响，发现微陀螺振动系统的检测灵敏度和带宽呈反比关系；微弹性梁的非线性刚度会使得载体角速度与检测输出呈非线性关系。

然而，以上研究大多采用的静电力模型仍为简谐力激励,也少见关于振幅跳跃现象机制的研究报道。事实上，无论平行板电容型静电驱动还是切向梳齿驱动，其静电力都分别与动、静极板的间距或交叠面积有关，因此应主要体现为参数激励驱动。此外，振幅跳跃现象在宏观结构振动系统中非常常见，相关机理研究较多[17-21]，如研究Duffing系统中振幅跳跃现象的机制[18-19]和振幅跳跃现象在双稳态压电发电系统的应用[20-21]，而在微陀螺振动系统中其行为机制却未被深入理解。事实上，振幅跳跃现象对微陀螺的稳定性和精度有着不容忽视的影响：振幅跳跃现象的出现意味着载体角速度稍有变动，微陀螺检测模态就会发生振幅突变，这是一种全局失稳行为，对应载体角速度和检测模态振幅之间的线性关系不复存在，即微陀螺的测量稳定性和精度遭到破坏。因此本文针对一类切向梳齿驱动型振动式微陀螺建立参数激励振动系统模型，分析设计参数和驱动参数对驱动和检测模态响应的影响规律，尤其是引起振幅跳跃和概周期振动等复杂运动的机制，从而为静电驱动微陀螺的设计和应用提供一定的理论依据。

1 动力学建模

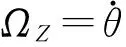
图1 切向梳齿驱动型振动式微陀螺结构Fig.1 Structure of a non-interdigitated comb-finger actuated vibratory micro-gyroscope

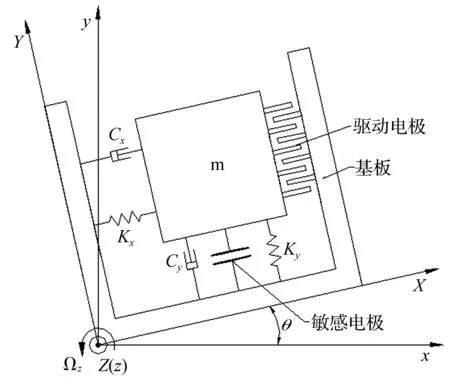
图2 切向梳齿驱动型振动式微陀螺简化模型Fig.2 Simplified model of a non-interdigitated comb-finger actuated vibratory micro-gyroscope

当微陀螺的载体绕Z轴以恒定角速度Ωz转动时，考虑弹性元件自身的质量远远小于振动元件质量m，忽略不计，可采用两自由度集总参数系统模型来描述微陀螺在X-Y平面内的振动特性。考虑图1中微陀螺的真空封装环境，空气阻尼与真空度有关，因此空气阻尼相对较小，其非线性因素可以被忽略，可假设驱动和检测方向阻尼均为线性，Cx,Cy分别为驱动和检测方向的线性阻尼系数；为充分考虑微梁刚度的非线性，设Kx1,Ky1分别为驱动和检测方向的线性刚度系数，Kx3,Ky3分别为驱动和检测方向的立方非线性刚度系数。利用拉格朗日方程，可建立常见的微陀螺分析模型：

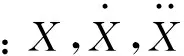
Fa(X,t)=-(r1X+r3X3)V2(t)

(2)

式中:r1和r3分别为线性和非线性静电常数，与驱动梳齿电容的设计参数，如齿数和几何分布直接相关；V(t)为驱动电压，为时间t的函数，为了方便研究参数激励的影响，并充分考虑交流电压的作用，这里将驱动电压表示为

(3)

式中:VA为交流电压幅值，ω0为频率。

为了简化动力学模型(1)，设

(4)

对式(1)进行整理，得到

(5)

考虑在驱动和检测方向上Ky3=Kx3,Cy=Cx，则系统式(5)成为

(6)

其物理参数取值如表1所示[6]。

表1 微陀螺物理参数值

2 动力学分析

本节主要求解和分析系统(6)的周期响应。首先，考虑系统的主参数共振和1∶1内共振情况，设

(7)

式中:σ1和σ2分别为驱动和检测方向的调谐参数，0<ε≪1。对变量重新标度如下：

(8)

则系统(6)成为

X″+X=ε2γ2X+2εγY′-εμX′-εkX3-εσ1X+
(εβ1X+εβ3X3)(1+cos(2T))

Y″+Y=ε2γ2Y-2εγX′-εμY′-εkY3-εσ2Y

(9)

为得到系统(9)的近似周期响应，设方程的摄动解形式为

式中:T0=T为快变时间尺度，T1=εT为慢变时间尺度。采用多尺度法对系统进行摄动，为使驱动和检测模态位移解不出现久期项，对比(ε0)和(ε1)系数，得到

(11)

和

(12)

对应式(12)右侧为零，可得到关于驱动和检测模态振幅a1,b1和相位角ψ1,ψ2的方程

(13)

消去式(13)中的ψ1和ψ2，可得到微陀螺系统关于振幅a1和b1的分岔方程

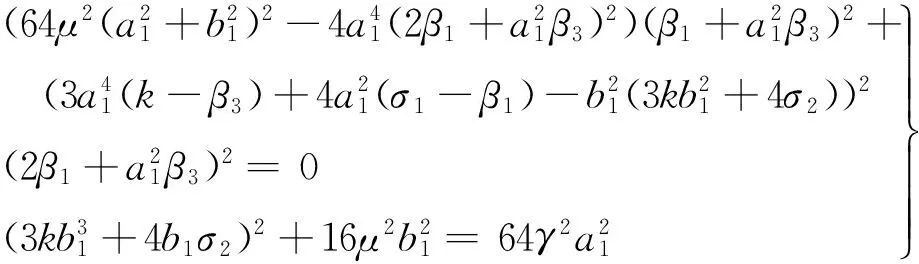
(14)

由式(11)和(14)即可确定系统(9)的近似周期解。以下分析解的稳定性。若周期解对应的特征方程

λ4+2μλ3+g2λ2+g1λ+g0=0

(15)

具有正实部的根，则该周期解不稳定，其中

(16)

因此，周期解产生Hopf分岔的临界条件为式(15)有一对纯虚根。在此设这对纯虚根λ=±iφ，代入(15)式，分离实虚部并化简，得到：

φ4-g2φ2+g0=0, -2μφ2+g1=0

(17)

由式(17)消去φ，则得到周期解产生Hopf分岔的系统参数条件，即

(18)

3 系统参数对响应的影响

本节主要讨论各系统参数对微陀螺振动系统的驱动和检测模态响应的影响。根据上节的式(10)和(13)可得到各系统参数所引起驱动和检测模态的响应曲线，其中周期解支的稳定性判断可根据式(15)和(16)，Hopf分岔点由(18)式得到。解析分析结果由数值模拟系统动力学响应进行验证。

给定载体的角速度，取ε=0.01，则驱动和检测方向的幅频响应如图3和图4所示。由图3和4可知，系统在共振点附近响应幅值较大，对应输出信号会比较明显，有利于检测。其中虚线部分代表近似周期解的失稳区域，很明显，失稳区域是幅频特性曲线上多解情况的中间解支，即幅频特性曲线上两个垂直切线点之间的虚曲线部分。在图3中，当σ1在2.40～3.08区间内，系统出现多解和跳跃现象；在图4中，当σ2在-2.47～-1.13区间内，系统出现多稳态解和跳跃现象，数值模拟也验证了该现象，从图上可以看出一次近似解与数值模拟结果非常吻合。根据图3和4，当σ1>0和σ2<0时，即主参数共振条件下，当驱动模态固有频率ω1，激励频率ω0和检测模态固有频率ω2满足ω1>ω0/2>ω2时，系统可能出现多稳态解和振幅跳跃现象。另外，在系统参数引起振幅跳跃现象之前，驱动模态固有频率的设计对检测模态振幅影响非常微弱(见图3(b))；类似地，检测模态固有频率对驱动模态振幅的影响也非常微小(见图4(a))。

图3 σ2=-1,γ=0.18时系统(9)的幅频响应 Fig.3 Amplitude-frequency responses of the system (9) for σ2=-1 and γ=0.18

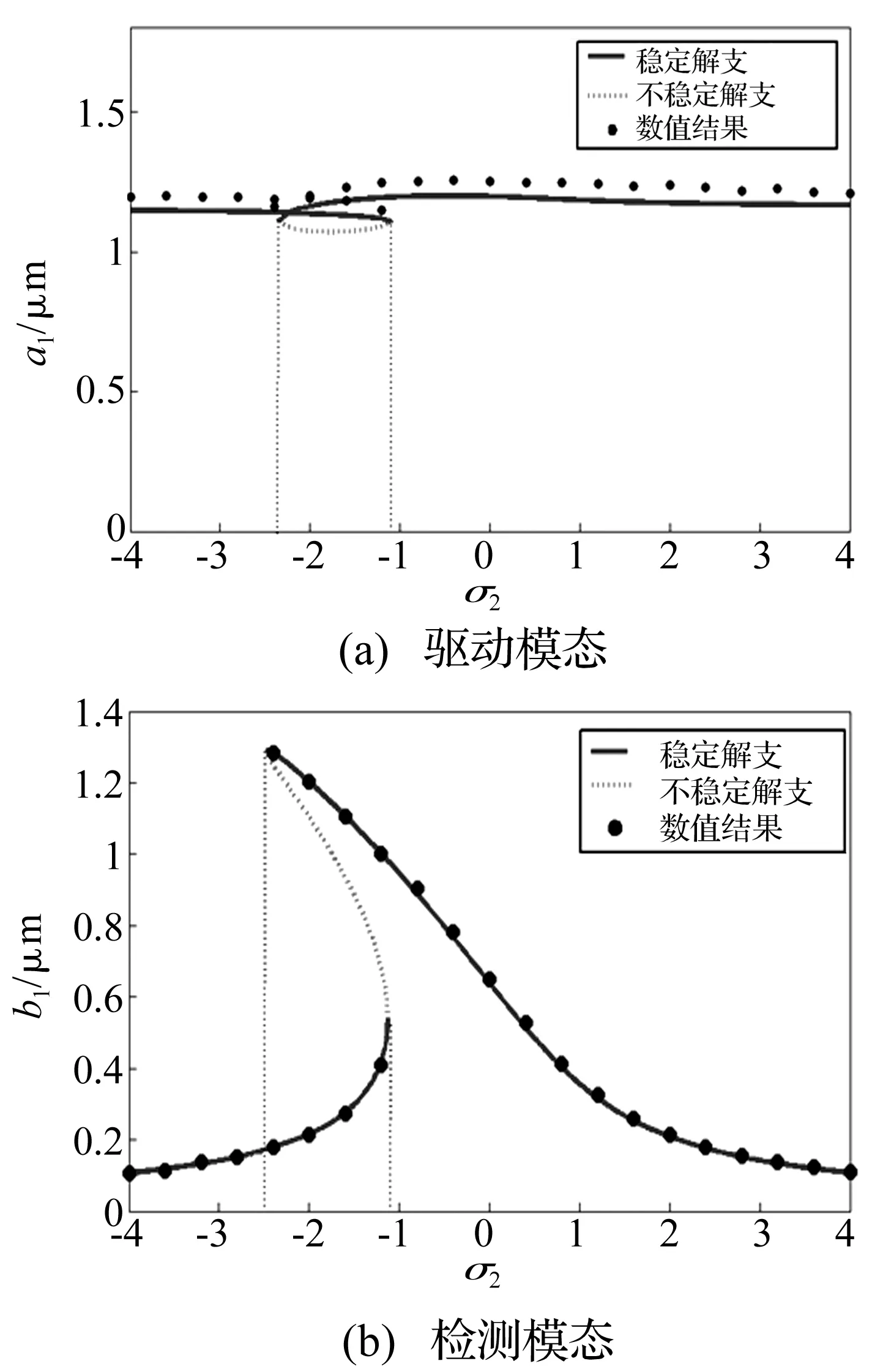
图4 σ1=2,γ=0.18时系统(9)的幅频响应Fig.4 Amplitude-frequency responses of the system (9) for σ1=2 and γ=0.18

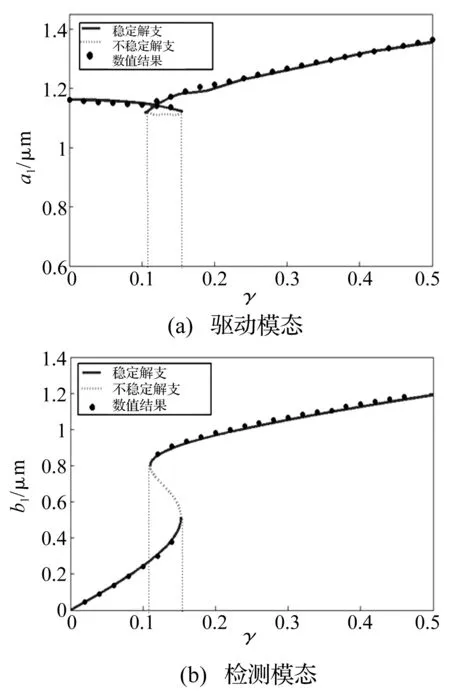
图5 σ1=2和σ2=-1时载体角速度对振动响应的影响Fig.5 Effects of the angular rate of substrate on the vibrating responses for σ1=2 and σ2=-1

载体角速度对微陀螺振动系统响应的影响如图5和图6所示。根据图5，对应较小的载体角速度下(即0<γ<0.110)，驱动模态振幅受载体角速度影响较小(见图5(a))，且检测模态振幅与载体角速度呈线性关系，斜率为2.41(见图5(b))，这一点完全符合微陀螺的工作原理；但当载体角速度继续增大时(0.110≤γ≤0.153)，系统会出现多稳态解和振幅跳跃现象。在一个正的驱动方向调谐参数下，不同载体角速度对应的系统(9)的幅频曲线如图6所示，由图6，在主参数共振情况下，在较小的载体角速度下系统的幅频响应曲线是连续的，如图6(a)中γ=0.05和γ=0.08两条曲线，不出现多解和振幅跳跃现象；载体角速度较大时才会产生多解和振幅跳跃现象，这与图5得到的结论相吻合，也与工程实际情况相一致。综合图5和图6，微陀螺正常工作存在一定的载体角速度范围，超出这个范围，即使微陀螺振动系统的驱动和检测模态有周期响应，仍会出现振幅跳跃现象。

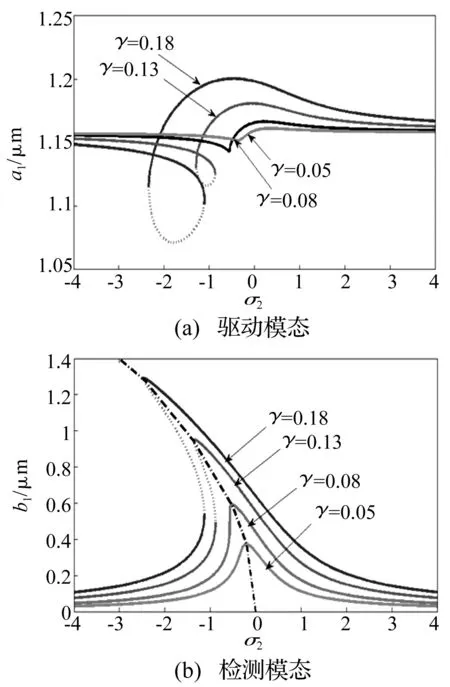
图6 σ1=2时不同载体角速度下系统(9)的幅频响应Fig.6 Amplitude-frequency responses of the system (9) under different values of angular rate of substrate when σ1=2

另外，考虑载体角速度较大、驱动模态固有频率偏离共振点，且频率关系仍满足ω1>ω0/2>ω2的情况。如当σ1=15,σ2=-1和γ=0.18时，系统的驱动和检测模态响应见图7。由时间历程图可知，系统发生了概周期振动。

图7 系统(1)的复杂响应Fig.7 Complex response of the system (1)

4 结 论

以一类典型的切向梳齿驱动型振动式微陀螺为研究对象，建立两自由度、具有刚度立方非线性和参数激励的振动系统动力学模型，运用多尺度法和分岔理论，结合数值验证，分析系统各参数对微陀螺驱动和检测模态的影响。得到以下主要结论：

(1)主参数共振和1∶1内共振情况下，驱动模态振幅较大，输出信号较明显，便于检测。

(2)在系统参数引起多稳态和振动跳跃现象前，驱动模态固有频率对检测模态振幅的影响，以及检测模态固有频率对驱动模态振幅的影响都非常微弱。

(3)主参数共振和1∶1内共振的情况下，即微陀螺的驱动模态固有频率ω1，检测模态固有频率ω2和激励频率ω0之比接近1∶1∶2时，若满足ω1>ω0/2>ω2，那么在较大的载体角速度下，微陀螺系统容易出现多稳态解和振幅跳跃现象；而在较小的旋转载体角速度下，系统不发生多解和振幅跳跃现象，且检测模态振幅与载体角速度呈线性关系，微陀螺检测精度较高。

(4)当驱动模态固有频率偏离主参数共振点，载体角速度的增大容易引起微陀螺振动系统的概周期响应。

[ 1 ] NASERI H, HOMAEINEZHAD M R. Improving measurement quality of a MEMS-based gyro-free inertial navigation system[J]. Sensors and Actuators A: Physical, 2014, 207: 10-19.

[ 2 ] 张丽杰, 常佶. 小型飞行器 MEMS 姿态测量系统[J] .振动、测试与诊断, 2010, 30(6): 699-702. ZHANG Lijie, CHANG Ji. MEMS-based attitude measurement system for miniature air vehicle[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 699-702.

[ 3 ] YOUNIS M I. MEMS linear and nonlinear statics and dynamics[M]. Springer NewYork, 2011.

[ 4 ] ACAR C, SHKEL A. Inherently robust micromachined gyroscopes with 2-DOF sense-mode oscillator[J]. Journal of Microelectromechanical Systems, 2006, 15(2): 380-387.

[ 5 ] SAID E A,KANBER M S, TAYFUN A. A high-performance silicon-on-insulator MEMS gyroscope operating at atmospheric pressure[J]. Sensors and Actuators A: Physical, 2007,135(1): 34-42.

[ 6 ] OROPEZA-RAMOS L A, BURGNER C, TURNER K L. Robust micro-rate sensor actuated by parametric resonance[J]. Sensors and Actuators A: Physical, 2009, 152(1): 80-87.

[ 7 ] PARK S, HOROWITZ R, TAN C W. Dynamics and control of a MEMS angle measuring gyroscope[J]. Sensors and Actuators A: Physical, 2008, 144(1): 56-63.

[ 8 ] Ali P, Hassan S. A parametric study on design of a microrate-gyroscope with parametric resonance[J]. Measurement, 2013, 46(8): 2661-2671.

[ 9 ] ACAR C, SHKEL A. MEMS vibratory gyroscopes[M]. Springer, NewYork, 2009.

[10] LIU K, ZHANG W, CHEN W, et al. The development of micro-gyroscope technology[J]. Journal of Micromechanics and Microengineering, 2009, 19(11): 113001.

[11] 罗跃生. 硅微型梳状线振动驱动式陀螺仪工作的微分方程模型[J]. 哈尔滨工程大学学报, 2003, 24(1): 49-53. LUO Yuesheng. Differential equation model for lateral comb drive micromachined silicon gyroscopes[J]. Journal of Harbin Engineering University, 2003, 24(1): 49-53.

[12] KENIG E, TSARIN Y A, LIFSHITZ R. Homoclinic orbits and chaos in a pair of parametrically driven coupled nonlinear resonators[J]. Physical Review E, 2011, 84(1): 016212.

[13] FRANCESCO B, FERRUCCIO R, ELISABETTA L, et al. Nonlinear dynamics of vibrating MEMS[J]. Sensors and Actuators A: Physical, 2007, 134(1): 98-108.

[14] 李欣业, 张利娟, 张华彪. 陀螺系统的受迫振动及其时滞反馈控制[J]. 振动与冲击, 2012, 31(9): 63-69. LI Xinye, ZHANG Lijuan, ZHANG Huabiao. Forced vibration of a gyroscope system and its delayed feedback control[J]. Journal of Vibration and Shock, 2012, 31(9): 63-69.

[15] 盛平，王寿荣，吉训生,等. 硅微机械谐振陀螺仪的非线性分析[J]. 中国惯性技术学报, 2006, 14(6): 60-63. SHENG Ping, WANG Shourong, JI Xunsheng, et al. Nonlinear analysis on silicon micromachined resonant gyroscope[J]. Journal of Chinese Inertial Technology, 2006, 14(6): 60-63.

[16] 文永蓬, 尚慧琳. 微陀螺动力学建模与非线性分析[J]. 振动与冲击, 2015, 34(4): 69-73. WEN Yongpeng, SHANG Huilin. Dynamic modeling and nonlinear analysis for a microgyroscope[J]. Journal of Vibration and Shock, 2015, 34(4): 69-73.

[17] 符毅强, 陈予恕, 侯磊,等. 反向旋转双转子系统滞后特性分析[J] . 振动与冲击, 2015, 34(15): 23-37. FU Yiqiang, CHEN Yushu, HOU Lei, et al.A counter-rotating dual-rotor system’s hysteretic characteristics[J]. Journal of Vibration and Shock, 2015, 34(15): 23-37.

[18] 张小龙, 东亚斌. Duffing型隔振的力传递率及跳跃现象的理论分析[J]. 振动与冲击, 2012, 31(6): 38-42. ZHANG Xiaolong, DONG Yabin. Theoretical analysis on force transmissibility and jump phenomena of Duffing spring type vibration isolator[J]. Journal of Vibration and Shock, 2012, 31(6): 38-42.

[19] 戎海武, 徐伟, 方同. 谐和与窄带随机噪声联合作用下Duffing 系统的参数主共振[J]. 力学学报, 1998, 30(2): 179-185. RONG Haiwu, XU Wei, FANG Tong. Principal response of Duffing oscillator tocombined deterministic and narrow-band random parametric excitation[J]. Acta Mechanica Sinica, 1998, 30(2): 179-185.

[20] 贾尚帅, 孙舒, 李明高. 基于谐波平衡法的双稳态压电发电系统非线性振动特性研究[J]. 振动与冲击, 2014, 33(6): 170-173. JIA Shangshuai, SUN Shu, LI Minggao. Non-linear vibration analysis of bistable piezoelectic power generation system based on harmonic balance method[J] . Journal of Vibration and Shock, 2014, 33(6): 170-173.

[21] 郭抗抗, 曹树谦. 考虑材料非线性时压电发电悬臂梁的主共振响应分析[J]. 振动与冲击, 2014, 33(19): 8-16. GUO Kangkang, CAO Shuqian. Primary resonance of cantilevered piezoelectric energy harvesters considering nonlinearities of piezoelectric material[J] . Journal of Vibration and Shock, 2014, 33(19): 8-16.

Nonlinear vibration behaviors of a micro-gyroscope system actuated by a parametric excitation

SHANG Huilin1, ZHANG Tao1, WEN Yongpeng2

(1.School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, China;2.College of Urban Railway Transportation, Shanghai University of EngineeringTechnology, Shanghai 201620, China)

For a typical non-interdigitated comb-finger actuated micro-gyroscope, a 2-DOF dynamic model with cubic nonlinear stiffness and parametric excitation was established. For the principal parametric resonance case and 1:1 internal resonance, the periodic solutions were obtained with the multi-scale method. Conditions of Hopf bifurcation of the periodic solutions were derived according to the theory of bifurcation. Then the dynamic responses of the system were simulated. Finally, the effect mechanism of the system’s parameters on the modal amplitudes and bifurcation behaviors was analyzed. It was shown that the variation of the excitation frequency is easy to cause various complex dynamic behaviors of the microgyroscope vibrating system, such as, multi-stable solution, amplitude jump phenomena and quasi-periodic responses under a large angular speed of the carrier and 1:1 internal resonance.

micro-gyroscope; electrostatic force; principal parametric resonance; multi-stable solution; amplitude jump phenomenon

国家自然科学基金面上项目(11472176);上海市自然科学基金(15ZR1419200)

2016-01-13 修改稿收到日期：2016-05-10

尚慧琳 女，副教授，1983年3月生

TH113.1; O327

A

10.13465/j.cnki.jvs.2017.01.015