含间隙RU-RPR解耦并联机构混沌与冲击现象

侯雨雷， 汪 毅， 井国宁， 曾达幸， 邱雪松， 李慧剑

(1. 燕山大学 机械工程学院，河北 秦皇岛 066004；2.燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

含间隙RU-RPR解耦并联机构混沌与冲击现象

侯雨雷1， 汪 毅1， 井国宁1， 曾达幸1， 邱雪松1， 李慧剑2

(1. 燕山大学 机械工程学院，河北 秦皇岛 066004；2.燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

针对含间隙机构中的混沌与冲击现象，以自主提出的RU-RPR(R为转动副，U为虎克铰，P为移动副)两转动解耦并联机构为研究对象，考虑运动副间隙，结合Lankarani-Nikravesh接触力模型与拉格朗日方程建立间隙机构动力学模型，分析不同的驱动速度和摩擦因数对机构中混沌现象与冲击的影响，同时探讨机构的稳定性与冲击现象的关系，并分析增设弹簧对机构动力学特性的影响。研究结果表明，改变驱动速度与摩擦因数时，冲击现象仍然存在，而机构可以由混沌运动变为周期运动，稳定性增强；机构的稳定性与冲击现象并没有必然的联系，且增加弹簧可以显著的减弱机构中的冲击程度。

并联机构；间隙；动力学；混沌；冲击

随着机械产品日益朝着高速、重载、高精度的目标发展，对机构动态性能的要求也越来越高，而不可避免的运动副间隙的影响愈发引起众多学者和工程界的重视。并联机构的独特优势及其广泛应用已为业界认可，作为多维的强非线性系统，并联机构包含着丰富的动力学特性，其能否适应更高的作业条件要求而继续得以应用并发展，将取决于动力学这一关键问题的解决程度。

目前，很多学者对含间隙机构的动力学建模[1-2]、动态特性[3-6]、混沌现象[7-10]、实验分析[11]等，已经进行了深入而广泛的研究。时兵等[12]针对大型重载机构虚拟样机中的间隙旋转铰，基于间隙矢量模型对一汽轮机阀门机构进行仿真计算，分析铰间隙、制造和装配误差等因素对机构动力学特性的影响。BAI等[13]采用一种混合接触力模型分析含间隙机构的磨损。RAHMANIAN等[8]绘制了含间隙曲柄滑块机构随间隙尺寸变化的分岔图。魏晓辉等[14]分析了装配间隙对起落架收放机构的影响，并提出了改进设计。余跃庆等[15]针对运动副间隙引起的并联机器人定位误差，探讨了运动副间隙误差引起的系统结构误差的变化规律，并提出优化补偿方法。赵刚练等[16]研究了含空间圆柱副间隙的动力学建模方法，并分析了圆柱副间隙对其他构件的动态特性的影响。王庚祥等[17]对含空间球面副间隙对新型减振平台4-SPS/CU并联机构动力学性能影响进行研究，分析球面副间隙对该并联机构运动学特性及驱动力的影响。赵宽等[18]分析了含间隙的曲柄滑块机构在考虑运动副间隙、摩擦力及系统参数具有随机性时的动力响应问题。

混沌是非线性动力系统所特有的且普遍存在的现象，混沌现象在有些情况下于机构性能有利，而在有些情况下将产生不良的影响，导致本来认为无论如何是安全和稳定的系统失灵，为工程系统的响应和可靠性增加了不确定因素。对并联机构进行混沌现象辨识，进而体现于动态设计中并实现有效的控制，对机构动态特性的优劣具有关键性的作用。

在间隙机构中，运动副元素之间的分离碰撞将产生冲击现象，严重的冲击会导致机构的运动精度降低，加剧磨损，对机构产生破坏，降低机构的使用寿命。现有的文献中，含间隙机构动态性能的分析已经比较普遍，而针对引起间隙机构动态性能恶化的冲击现象却鲜有学者进行深入的研究。

机构的稳定性是指机构保持原有运动状态的能力。当给定机构的驱动为周期性时，如果机构处于周期运动状态，则机构是稳定的，而如果机构处于混沌运动状态，则机构是不稳定的。运动副的间隙会造成机构运动的不确定性，机构的动态特性在某种条件下会剧烈地变化，而且呈现出混沌特性[19]。OLYAEI等[19]通过某种控制方法使机构由混沌状态变成不混沌状态，从而使机构由不稳定状态变成稳定状态。ZHANG等[4]对含多间隙的平面并联机构进行动力学建模，分析了载荷、运动速度和运动轨迹对机构稳定性的影响。王威等[20]以平面四杆机构为例研究了间隙与干摩擦对机构运行稳定的影响。

本文即在此背景下，以含间隙RU-RPR解耦并联机构[21]为研究对象，利用Lankarani-Nikravesh接触力模型计算法向接触力，将修正的Coulomb摩擦力法则嵌入到切向接触力的计算过程中，应用拉格朗日方程建立间隙机构动力学模型，采用变步长四阶龙格库塔法予以数值求解，辨识解耦并联机构非线性动力学中的混沌现象，分析不同的因素对机构中混沌与冲击现象的影响，探讨机构的稳定性与混沌现象间关系，并分析增设弹簧对机构冲击现象的影响，以期对并联机构动力学研究有所深化，为研制高效、高速和稳定的并联装备提供理论依据与技术支撑。

1 转动副间隙中的接触力分析

(1)

其单位矢量为

n=e/e

(2)

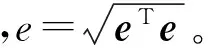
图1 转动副间隙模型Fig.1 Gap model of the rotation pair

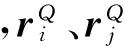
(3)

式中:Ri、Rj分别为轴承与轴的半径。

式(3)两边对时间求导，可得碰撞点速度为

(4)

将碰撞点的相对速度投影到碰撞平面的切向和法向平面，可得相对的法向速度vn和切向速度vt，其标量形式为

(5)

式中:切向矢量t可以通过将n逆时针旋转90°获得。

轴承和轴的穿透深度为

δ=e-c

(6)

式中:c为半径间隙，且c=Ri-Rj。当δ为正值时，轴承与轴接触，反之，轴承与轴没有接触。

碰撞过程中必然产生碰撞力，导致一定的冲击、振动，从而对机构的性能造成不利影响。因此，采用一种合适的接触力模型来估算碰撞过程中的碰撞力非常重要。本文选用Lankarani-Nikravesh接触力模型[22]，该模型既考虑了碰撞过程中的能量损失，又较全面地考虑了碰撞体的材料属性、局部弹性变形以及碰撞速度等信息[23]，广泛用于含间隙机构的动力学分析。轴对轴承的法向接触力的表达式为

(8)

(9)

式中:cf为摩擦因数；v0、v1为给定的速度界限。

该法则可以防止切向接触力的方向突变，从而有利于数值积分的稳定。

轴对轴承的碰撞力可表示为

(10)

式中: fix、fiy分别为轴对轴承的碰撞力在X方向和Y方向上的分量。

2 含间隙RU-RPR解耦并联机构动力学建模

2.1 RU-RPR解耦并联机构组成

RU-RPR两转动解耦并联机构如图2所示，该机构由定平台、动平台以及连接两平台的两条支链组成，从定平台到动平台，第一条分支链依次由转动副和虎克铰相连，第二条分支链依次由转动副、移动副和转动副相连。其中，第二条分支中移动副的移动方向垂直于该分支两个转动副的轴线，两分支中与固定平台相连的两转动副轴线相互平行且与虎克铰的一条轴线平行，虎克铰的另一条轴线与第二分支中与动平台相连的转动副轴线重合。

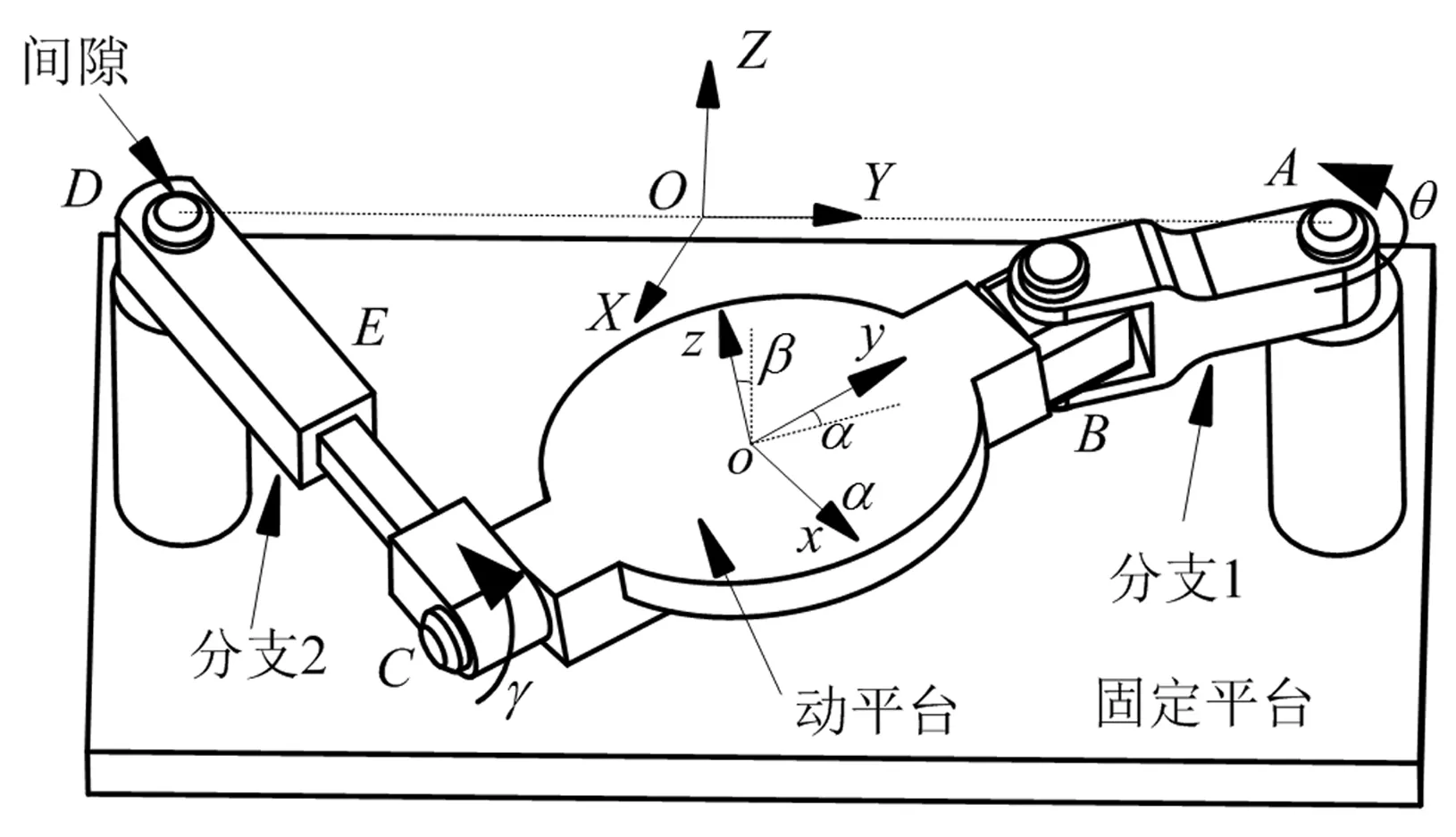
图2 RU-RPR两转动并联机构组成示意图Fig.2 Composition schematic of RU-RPR 2-DOF rotational parallel mechanism

在定平台上固连定坐标系O-XYZ，其中，坐标原点O为与连线中点在定平台平面的投影，Z轴竖直向上，Y轴与和定平台相连的两转动副A、D轴线垂直并指向A；在动平台上固连动坐标系o-xyz，其中，坐标原点o建立在动平台几何中心，y轴和分支2中与动平台相连的转动副的轴线共线，方向指向虎克铰，z轴与动平台平面垂直，方向向上。机构处于初始位置时，AB与BC共线。

以RU-RPR并联机构第一分支的转动副A和第二分支与动平台相连的转动副C作为主动副，θ与γ分别表示转动副A、转动副C的旋转角度；α与β分别表示动平台绕动坐标系的z轴和y旋转角度。

θ、γ为输入角度，而α和β为输出角度。显见，θ与α一一对应，而γ与β也是一一对应关系，所以，RU-RPR并联机构绕y轴和z轴的两转动自由度即两转动互不影响。因此，在研究转动副D处的间隙时，可暂不考虑机构绕y轴的转动，而只考虑动平台绕z轴(铅垂方向)的转动，故可将RU-RPR解耦并联机构视作一个平面四杆机构，其等效机构简图如图3所示。

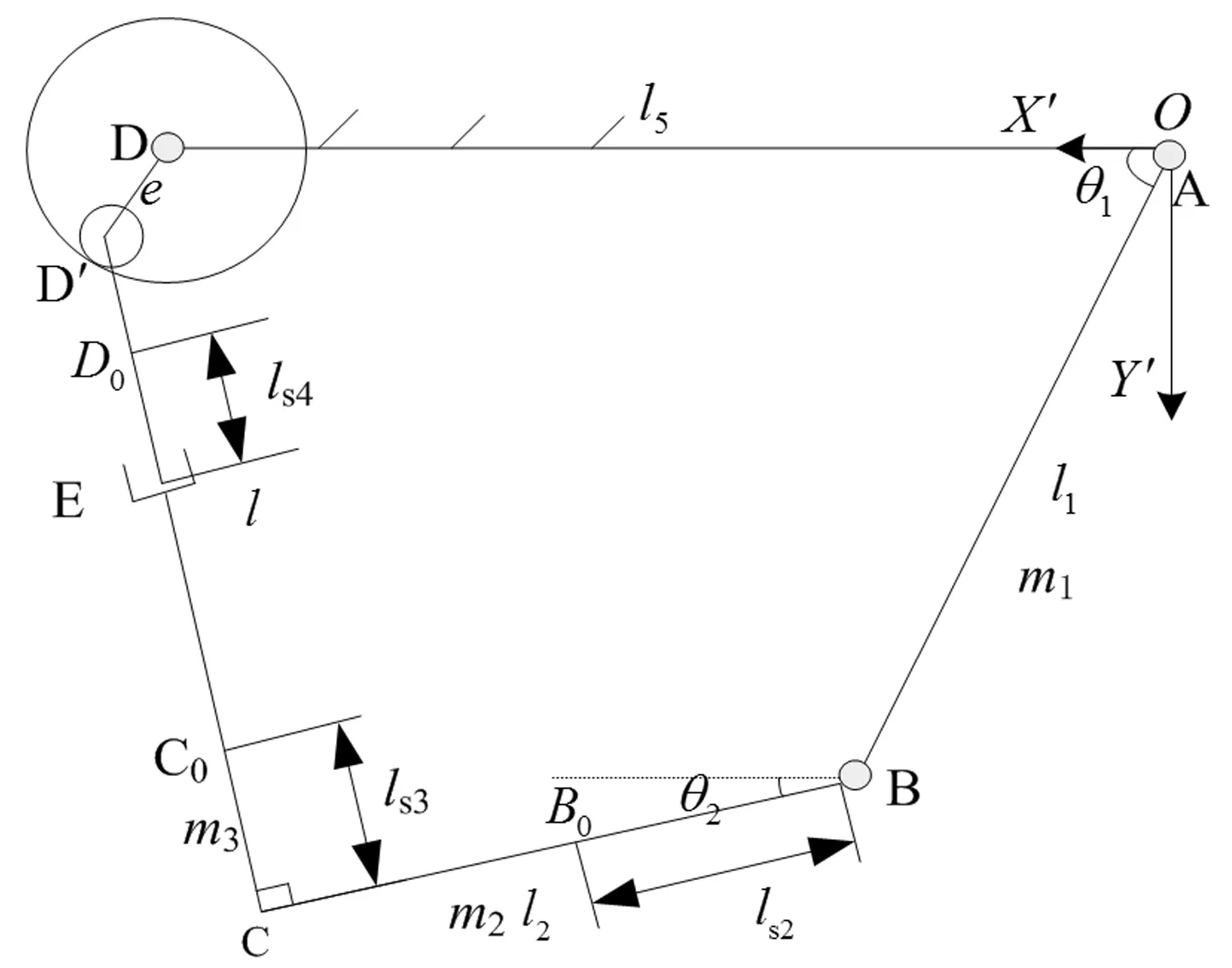
图3 含间隙RU-RPR并联机构等效机构简图Fig.3 Schematic diagram of equivalent agencies of RU-RPR parallel mechanism with clearance

2.2 含间隙RU-RPR并联机构运动分析

如图3所示，针对等效的含间隙RU-RPR解耦并联机构建立平面坐标系X′O′Y′，并对后续动力学分析所需相关参数定义如下：l1、θ1、J1分别表示杆AB的长度、转角以及对转动连接副A的转动惯量；l2、ls2、θ2、m2、Js2分别表示杆BC的长度、质心B0距运动副B的距离、转角(与X′轴正向的夹角)、质量以及对自身质心的转动惯量；m3、ls3、Js3分别表示杆CE的质量、质心C0与C之间的距离以及对自身质心的转动惯量；m4、ls4、Js4分别表示杆DE的质量、质心D0距运动副E的距离以及对自身质心的转动惯量；l表示CD之间的距离，l5表示机架的长度；x,y分别表示间隙(图中小圆表示轴，大圆表示轴承)的横向、纵向分量，即轴和轴承间的横向、纵向相对位移分量。

由于间隙的存在，此时该四杆机构有三个自由度。设定机构的广义坐标为：杆AB的转动角度θ1，轴销与轴承横向相对位移x，轴销与轴承的纵向相对位移y。通过引进扰动坐标，建立含间隙解耦并联机构的运动学模型。

对无间隙四杆机构，有如下的封闭方程

(11)

式中:θ20为无间隙机构中BC杆转角，l0为无间隙机构中CD杆的长度，cθ1=cosθ1，sθ1=sinθ1，其余类似。

对D处含一个间隙的四杆机构，有如下封闭方程

(12)

利用扰动坐标法，含间隙机构的转角均由无间隙机构的转角加上一个小扰动角构成，杆长度由无间隙机构的长度加上一个小的扰动长度构成。于是有

(13)

将式(13)代入式(12)中，根据三角公式和等价无穷小概念化简，可得

(14)

联立式(11)和式(14)，得

(15)

则式(15)可简化为

(16)

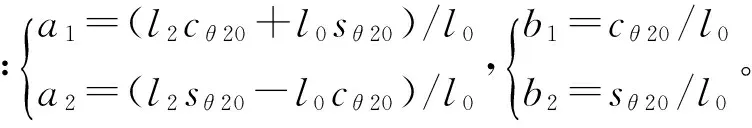
整个RU-RPR并联机构的动能T及势能V分别为

(17)

式中:F=Js2+m2ls22+Js3+m3l22+Js4+m3ls32+m4ls42，G=m3l1l2+m2l1ls2。

拉格朗日函数为

L=T-V

(18)

进而，拉格朗日运动方程可表示为

(19)

式中:Qj表示非保守系统中对应广义坐标qj的广义力，可以表示为

(20)

式中:Fi和Mi分别为作用在物体i质心的外力、外力矩，ri、φi分别为物体i质心的移动位移和转动角度。

在小学数学教学中培养学生的自主学习能力，需要加强对数学课程的策略改革，创新教学方式，激发学生的学习兴趣，促使学生积极进行学习活动，鼓励学生进行自主学习，提高学生的自主学习能力，促进学生素质能力的培养。

由式(20)，广义力可以表示为

(21)

将式(18)、式(21)代入式(19)，可得

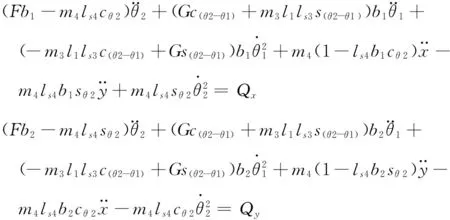
(22)

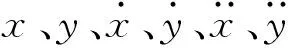
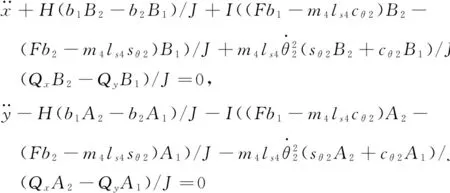
(23)

式中:

3 含间隙RU-RPR并联机构动力学数值仿真

机构中轴承与轴之间存在碰撞与非碰撞两种状态，而在分析每次碰撞的初始碰撞速度及碰撞面的方向时，精确的检测出碰撞点至关重要。已知轴承与轴发生碰撞的条件为

δ(tn)δ(tn+1)≤0

(24)

则在时间间隔tn与tn+1之间至少发生一次碰撞。碰撞时间非常短暂，故为保证计算效率与精度，采用变步长四阶龙格库塔法进行数值积分，当碰撞深度大于积分误差时，积分步长设定为前一个步长的一半，重新计算直至满足误差要求，本文借鉴文献[25]中的方法来控制步长。

式(23)包含两个二阶非线性方程，采用变步长四阶龙格库塔法予以求解。机构杆件形状参见图2，多选用长方形和圆柱形，其材料为45钢，则可得到RU-RPR机构相关参数如下：

l1=130 mm，l2=308 mm，ls2=154 mm，ls3=80 mm，ls4=54 mm，l5=524 mm，J1=7.351×10-3kg·mm3，Js2=6.160×10-2kg·mm3，Js3=5.772×10-3kg·mm3，Js4=3.008×10-3kg·mm3，m2=8.516 kg，m3=1.161 kg，m4=1.405 kg。

机构动力学仿真参数如表1所示，机构初始时杆OB与杆BC共线，机构驱动角速度为ω=10π rad/s。选取计算了2个周期的仿真结果，机构碰撞深度、接触力和轴心轨迹分别如图4(a)、图4(b)和图4(c)所示；图4(d)为机构Poincare映射图，计算了500个映射点。Poincare映射[8]可以方便地进行混沌辨识。Poincare映射上的一个点及少数离散点、闭合曲线、成片的具有分形结构的密集点分别表示系统的周期运动、拟周期运动和混沌运动。

图4(a)为轴承与轴之间的穿透深度，由图4(a)可知，轴与轴承在分离和碰撞之间不断变换，并非处于连续接触的状态。图4(c)中轴心轨迹图也可体现该特点(其中虚线圆表示轴承边界，该圆以轴承为中心为圆心，以轴承半径为半径)。轴与轴承在不断的分离与碰撞过程中，必然产生冲击现象，而图4(b)中高频振荡的接触力曲线也印证了此现象，且图4(a)中穿透深度振荡的时间点与图4(b)中接触力振荡的时间点是一致的。图4(d)中间隙处相对位移x与相对位移y的Poincare映射为具有一定的规律的密集点，表现为混沌状态。

表1 RU-RPR并联机构动力学仿真参数

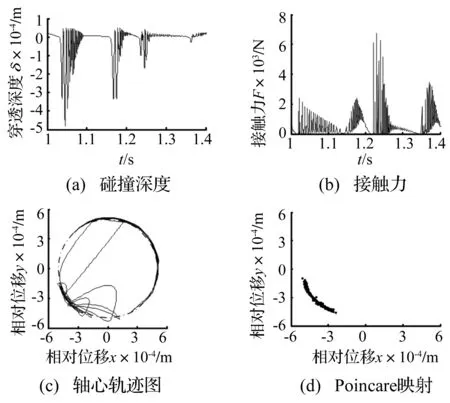
图4 含间隙RU-RPR并联机构的动力学响应Fig.4 Dynamic responses of RU-RPR parallel mechanism with clearance

4 RU-RPR并联机构动力学特性参数影响分析

驱动速度以及摩擦因数是影响机构动态性能的重要因素。如下将根据接触力、轴心轨迹以及Poincare映射分析不同的驱动速度及不同的摩擦因数对机构中冲击现象的影响，同时探讨机构稳定性与冲击现象的相互关系。

首先依据表1所列参数，参照前述仿真方法，依次取驱动速度为2π rad/s、8π rad/s、20π rad/s、40π rad/s，所得相应的机构接触力、轴心轨迹及Poincare映射分别如图5～图7所示。

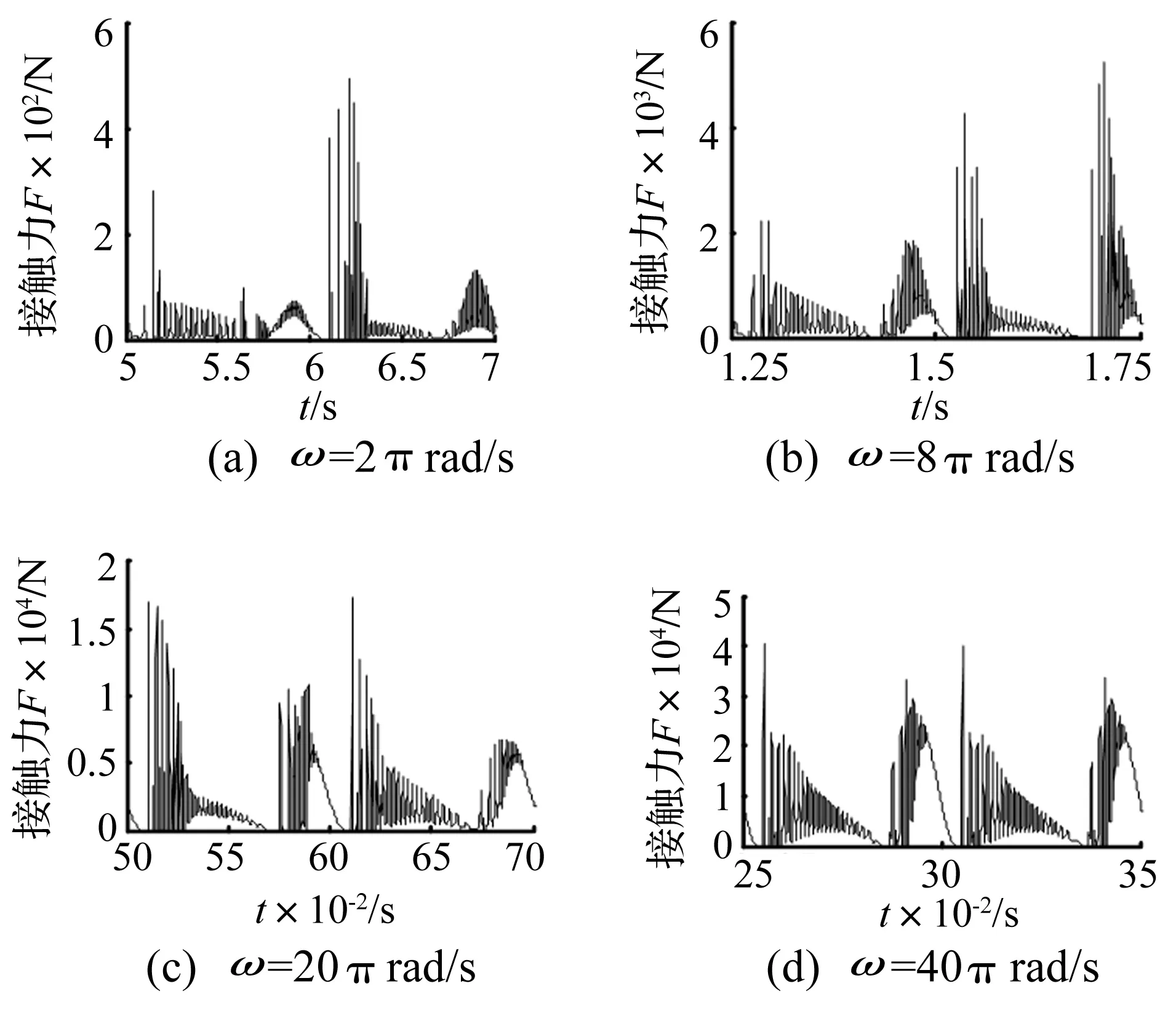
图5 不同驱动速度下RU-RPR机构的接触力Fig.5 Contact forces of RU-RPR mechanism at different driving speeds

由图5可看出，随着驱动速度的增加，接触力曲线的峰值增大，意味着随着驱动速度的增大，轴与轴承之间的穿透深度更大，轴与轴承之间的冲击现象更严重，图6也体现了该特点。

图6 不同驱动速度下RU-RPR机构的轴心轨迹图Fig.6 Axle center trajectory diagrams of RU-RPR mechanism at different driving speeds

图7表明，随着驱动速度的增大，机构中的混沌现象减弱，甚至形成周期运动，机构的稳定性增强。而图6显示出在各种驱动速度下，轴与轴承之间始终无法在整个运动阶段连续接触，即冲击现象依然存在。由此说明机构的稳定性与冲击现象并没有必然的联系。

其次，令驱动速度为5πrad/s，按摩擦系数依次取0.01、0.02、0.05、0.1四种情况，分析机构接触力、轴心轨迹及Poincare映射分别如图8～图10所示。

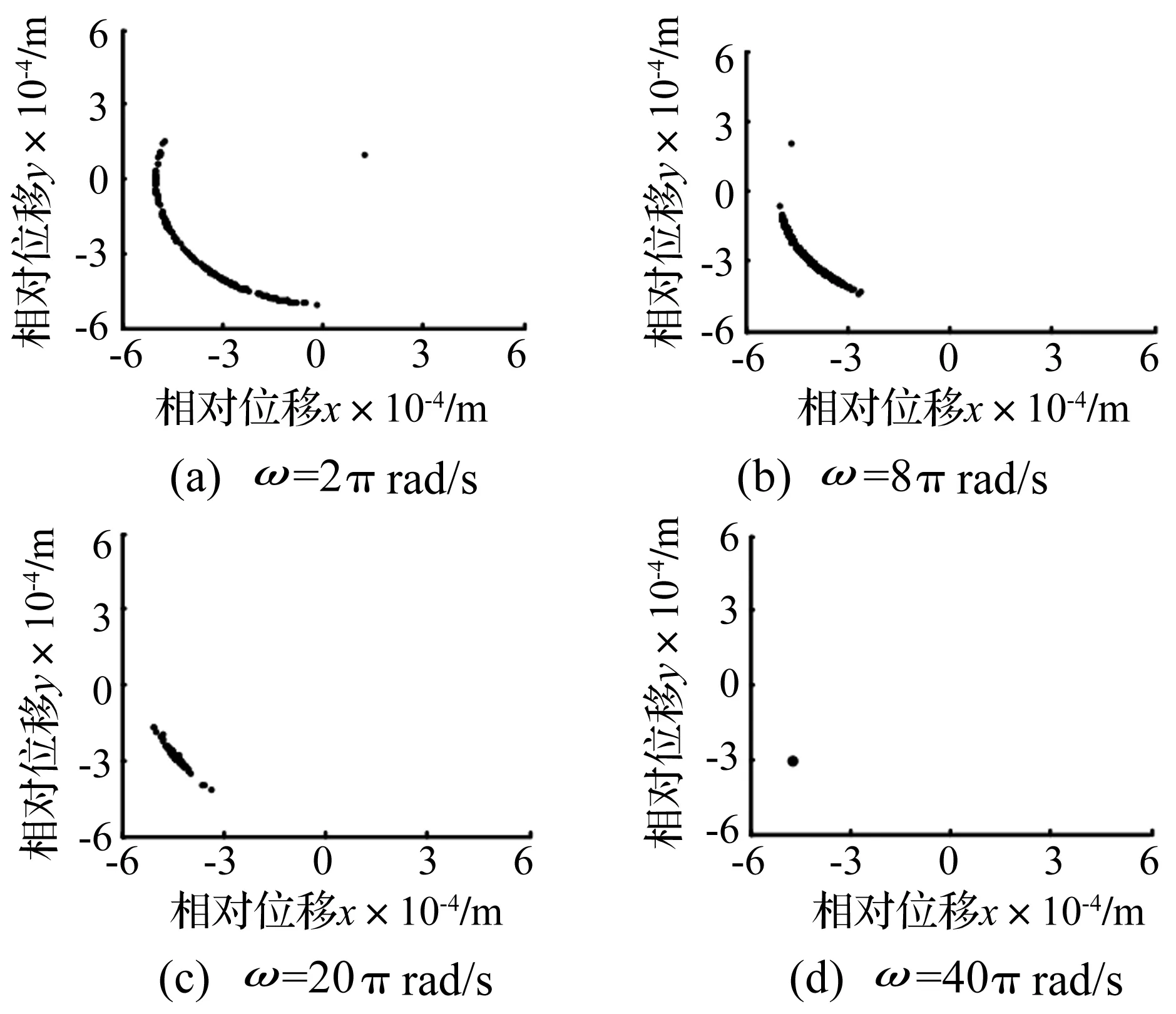
图7 不同驱动速度下RU-RPR机构的Poincare映射Fig.7 Poincare mapping diagrams of RU-RPR mechanism at different driving speeds

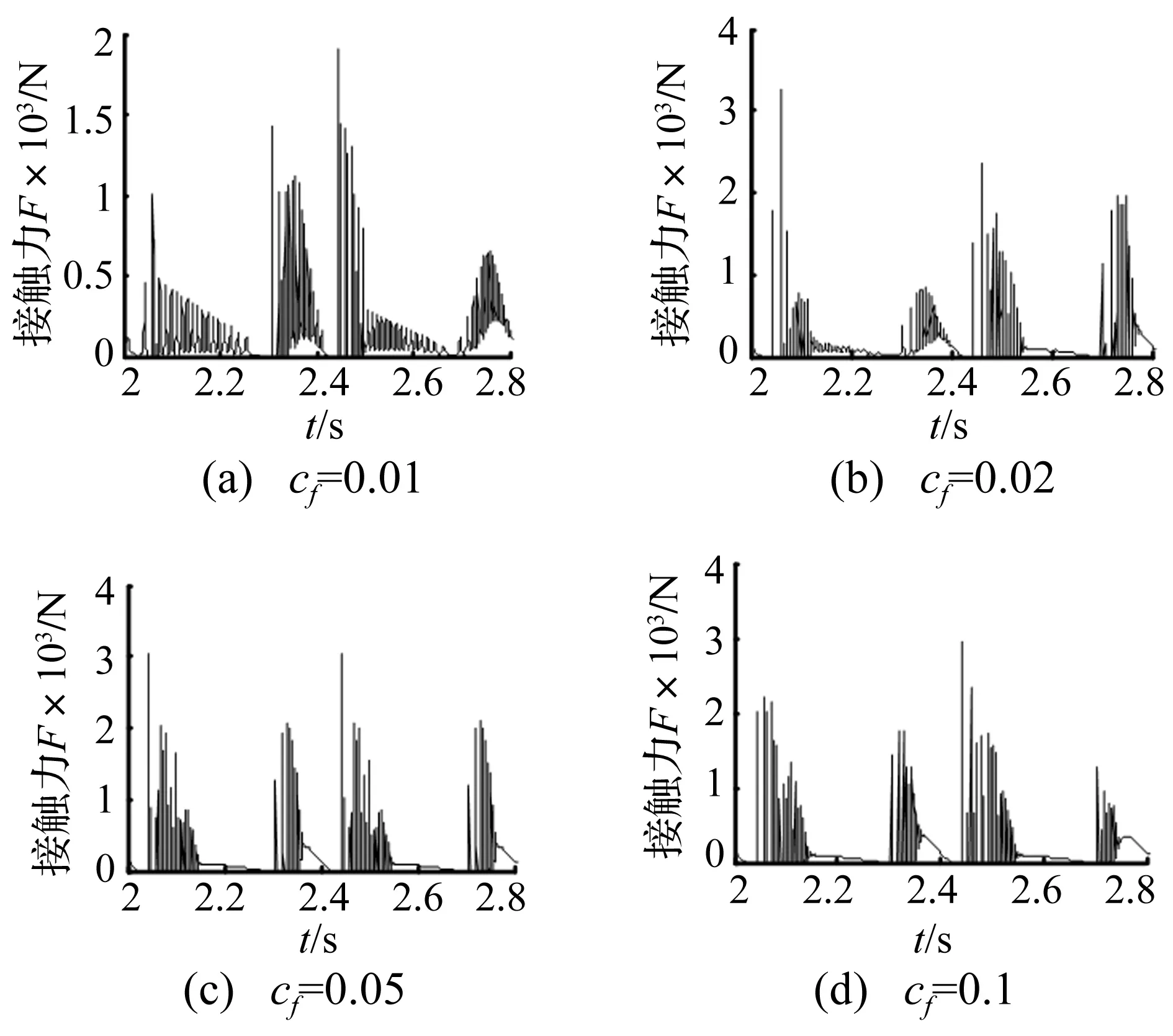
图8 不同摩擦系数下RU-RPR机构的接触力Fig.8 Contact forces of RU-RPR mechanism at different friction coefficients

由图8可知，当摩擦系数比较小时，接触力的峰值随着摩擦系数的增大而增大，冲击现象更为严重；而当摩擦系数较大时，随着摩擦系数增大，接触力的峰值几乎不变，冲击现象的程度基本保持稳定。

图10表明，摩擦系数越大，机构中的混沌现象越弱，机构的稳定性增强；但是轴与轴承之间的冲击碰撞依然存在(参见图9)，也再次说明机构的稳定性与冲击现象间并不存在必然的联系。

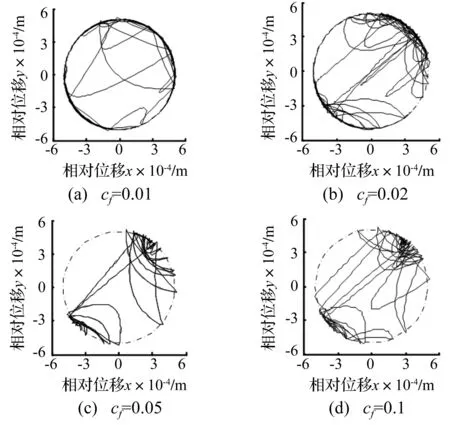
图9 不同摩擦系数下RU-RPR机构的轴心轨迹图Fig.9 Axle center trajectory diagrams of RU-RPR mechanism at different friction coefficients

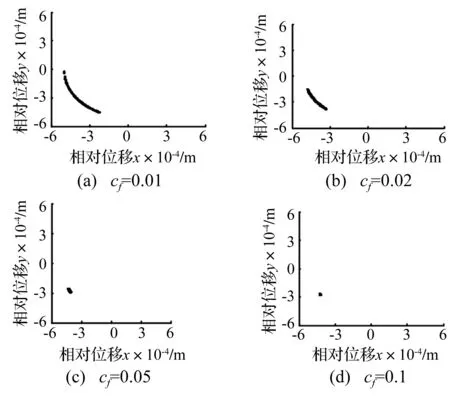
图10 不同摩擦系数下RU-RPR机构的Poincare映射Fig.10 Poincare mapping diagrams of RU-RPR mechanism at different friction coefficients

5 RU-RPR并联机构间隙影响的控制

根据RU-RPR并联机构动态特性参数影响分析，随着驱动速度或摩擦系数的增大，机构中的混沌现象减弱，机构的稳定性增强，但轴与轴承之间始终无法连续接触，冲击现象依然存在，甚至更加严重，而这必将降低机构的精度、寿命等，影响其正常工作。

故此，为减少轴与轴承之间的冲击，考虑在杆DE的质心与机架OD的几何中心之间增加一个弹簧，如图11所示。设弹簧原长为Ls0，刚度系数为ks，伸长后弹簧长度为Ls，则增加弹簧后RU-RPR机构的势能为

(25)

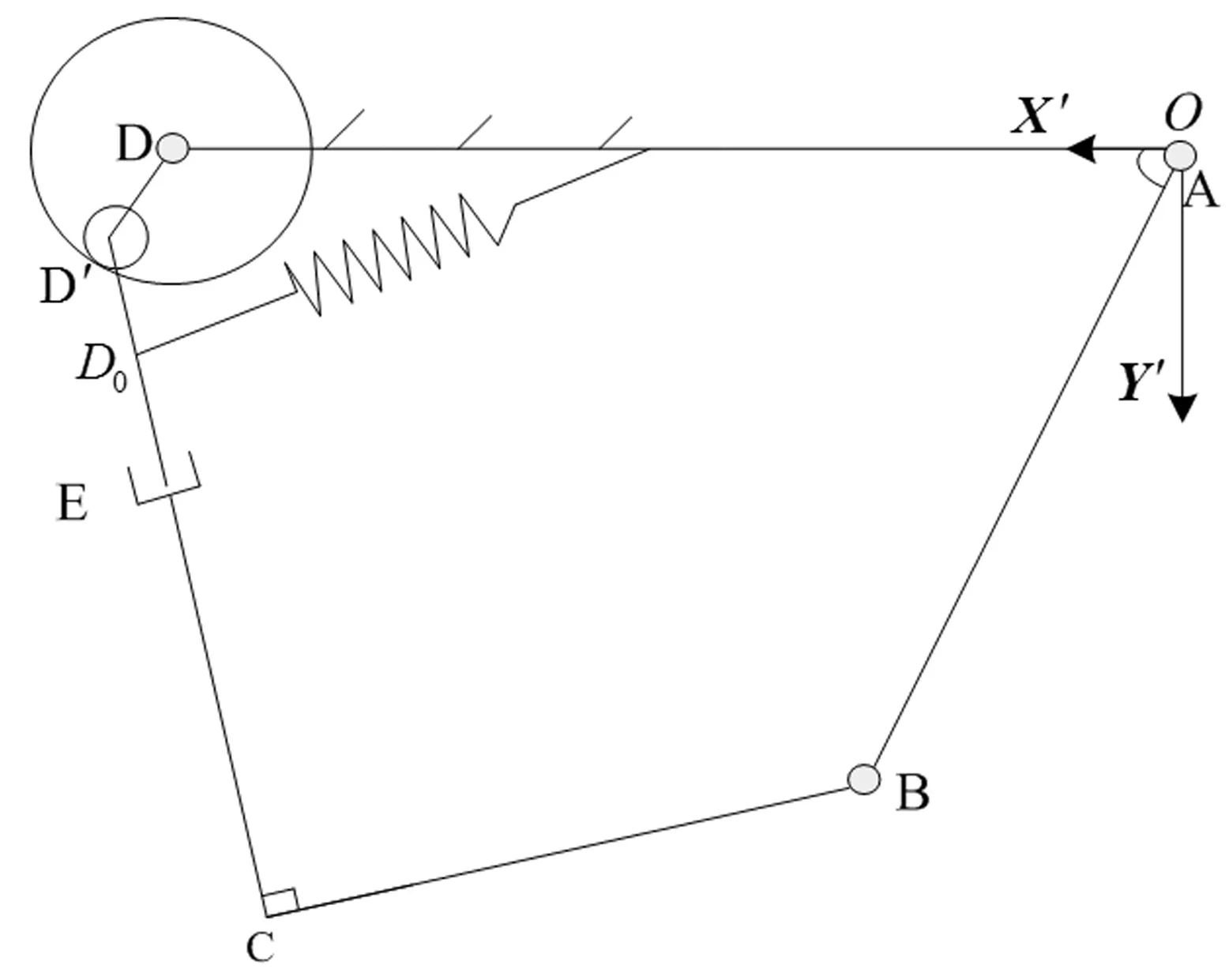
图11 增加弹簧后的RU-RPR机构简图Fig.11 RU-RPR mechanism diagram after adding the spring

为了达到预期的效果，使弹簧始终处于拉伸状态，且设定弹簧的原长为0.15 m，刚度系数为1 000 N/m，驱动速度ω=10π rad/s，其它动力学参数参照表1，仿真结果如图12所示。由图12(a)可知，增加弹簧后，轴与轴承之间始终连续接触，没有发生冲击现象，图12(b)、(c)也说明该特点。此外，对比图12(b)与图4(b)可知，增加弹簧后，接触力波动趋于平缓，且最大值由6 778降为1 629，降低了76%。图12(d)则表明增加弹簧后，机构中的混沌现象消失。

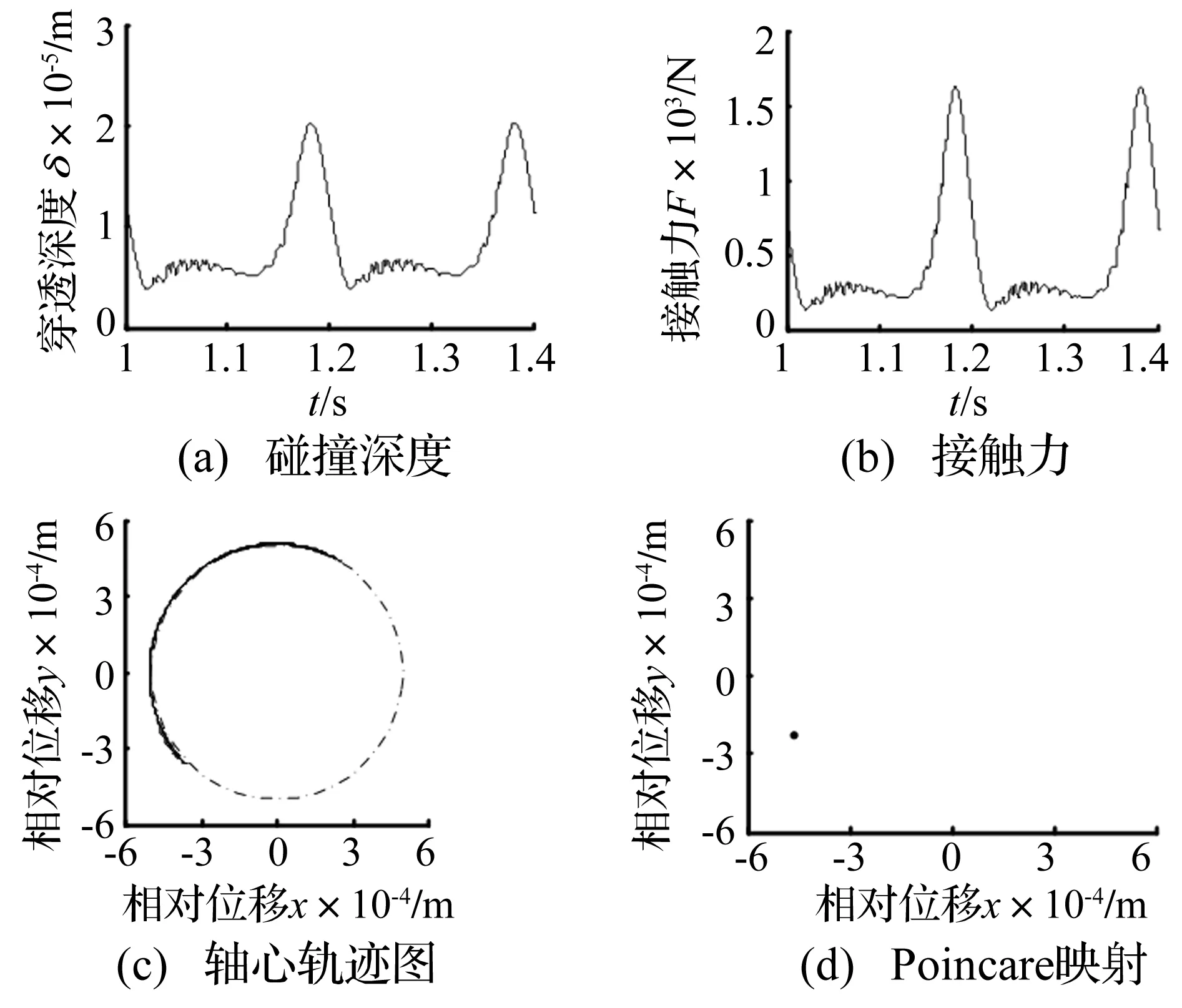
图12 增设弹簧后RU-RPR并联机构的动力学响应Fig.12 Dynamic responses of RU-RPR parallel mechanism after adding spring

6 结 论

(1)利用Lankarani-Nikravesh接触力模型、修正的Coulomb摩擦力法则和拉格朗日方程建立了含间隙RU-RPR解耦并联机构的动力学模型，借助变步长四阶龙格库塔法予以求解，动力学仿真结果表明RU-RPR机构转动副中间隙的存在使得机构在某种条件下存在混沌和冲击现象。

(2)当含间隙RU-RPR机构中驱动速度、摩擦系数增大时，机构由混沌运动变为周期运动，即机构的稳定性提高，而冲击现象依然存在，说明机构的稳定性与冲击现象并没有必然的联系，且通过增加弹簧并预紧能够有效消除机构中的冲击现象，对高可靠性并联装备的设计与控制具有一定的理论参考意义和实践应用价值。

[ 1 ] 白争锋. 考虑铰间间隙的机构动力学特性研究[D]. 哈尔滨：哈尔滨工业大学，2011.

[ 2 ] FLORES P. Dynamic analysis of mechanical systems with imperfect kinematic joints[D].Portugal: Universidade Do Minho, 2004.

[ 3 ] 王庚祥，刘宏昭. 考虑球面副间隙的4-SPS/CU并联机构动力学分析[J]. 机械工程学报，2015, 51(1): 43-51. WANG Gengxiang, LIU Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]. Journal of Mechanical Engineering, 2015, 51(1): 43-51.

[ 4 ] ZHANG Xuchong, ZHANG Xianmin, CHEN Zhong. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints[J]. Mechanism and Machine Theory, 2014, 78(8): 105-115.

[ 5 ] 白争锋, 赵阳, 赵志刚. 考虑运动副间隙的机构动态特性研究[J]. 振动与冲击, 2011, 30(11): 17-20. BAI Zhengfeng, ZHAO Yang, ZHAO Zhigang. Dynamic characteristics of mechanisms with joint clearance[J]. Journal of Vibration and Shock, 2011, 30(11): 17-20.

[ 6 ] 张增磊, 巫世晶, 赵文强, 等. 含间隙高速多连杆传动机构动力学特性研究[J]. 振动与冲击, 2014, 33(14): 66-71. ZHANG Zenglei, WU Shijing, ZHAO Wenqiang, et al. Dynamic characteristics of high-speed multi-link transmission mechanisms with clearance[J]. Journal of Vibration and Shock, 2014, 33(14): 66-71.

[ 7 ] 侯雨雷，汪毅，李明洋，等.一种含间隙两转动一移动解耦并联机构混沌现象辨识[J]. 中国机械工程，2015, 26(13): 1759-1766. HOU Yulei, WANG Yi, LI Mingyang, et al. Chaos identification of two rotational and one translational decoupled parallel mechanism concerning clearance[J]. China Mechanical Engineering, 2015, 26(13): 1759-1766.

[ 8 ] RAHMANIAN S, GHAZAVI M R. Bifurcation in planar slider-crank mechanism with revolute clearance joint[J]. Mechanism and Machine Theory, 2015, 91(5): 86-101.

[ 9 ] TANG Yuanguang, CHANG Zongyu, DONG Xiaogang, et al. Nonlinear dynamics and analysis of a four-bar linkage with clearance[J]. Frontiers of Mechanical Engineering, 2013, 8(2): 160-168.

[10] 何文运, 张俊红, 马梁. 剪式齿轮传动机构非线性动力学特性研究[J]. 振动与冲击, 2015, 34(15): 115-121. HE Wenyun, ZHANG Junhong, MA Liang. Nonlinear dynamic characteristics of a scissor gear transmission system[J]. Journal of Vibration and Shock, 2015, 34(15): 115-121.

[11] ERKAYA S, DOGAN S, ULUS S. Effects of joint clearance on the dynamics of a partly compliant mechanism:Numerical and experimental studies[J]. Mechanism and Machine Theory, 2015, 88(2): 125-140.

[12] 时兵，金烨. 面向虚拟样机的机构间隙旋转铰建模与动力学仿真[J]. 机械工程学报，2009, 45(4): 299-303. SHI Bing, JIN Ye. Dynamic simulation and modeling of revolute clearance joint for virtual prototyping[J]. Journal of Mechanical Engineering, 2009, 45(4): 299-303.

[13] BAI Zhengfeng, ZHAO Yang, CHEN Jun. Dynamics analysis of planar mechanical system considering revolute clearance joint wear[J]. Tribology International, 2013, 64(3): 85-95.

[14] 魏小辉, 王钰龙, 印寅, 等. 某起落架收放联动机构故障分析及改进设计[J]. 中国机械工程，2014, 25(3): 399-403. WEI Xiaohui, WANG Yulong, YIN Yin, et al. Failure analysis and improved design of a landing gear retraction mechanism[J]. China Mechanical Engineering, 2014, 25(3): 399-403.

[15] 余跃庆, 田浩. 运动副间隙引起的并联机器人误差及其补偿[J]. 光学精密工程，2015, 23(5): 1331-1339. YU Yueqing, TIAN Hao. Error and compensation of parallel robot with joint clearances[J]. Optics and Precision Engineering, 2015, 23(5): 1331-1339.

[16] 赵刚练, 姜毅, 郝继光, 等. 考虑圆柱铰链间隙的多刚体系统动力学计算方法[J]. 振动与冲击, 2013, 32(17): 171-176. ZHAO Ganglian, JING Yi, HAO Jiguang. Computational method of rigid mllltibody system dynamics considering cylindrical joint clearance[J]. Journal of Vibration and Shock, 2013, 32(17): 171-176.

[17] 王庚祥, 刘宏昭, 邓培生. 考虑球面副间隙的并联机构动力学模型[J]. 振动与冲击, 2014, 33(10): 43-49. WANG Gengxiang, LIU Hongzhao, DENG Peisheng. Dynamic modeling for a parallel mechanism considering spherical joint clearance[J]. Journal of Vibration and Shock, 2014, 33(10): 43-49.

[18] 赵宽, 陈建军, 曹鸿钧, 等. 含间隙曲柄滑块系统动力响应的随机性分析[J]. 振动与冲击, 2014, 33(11): 130-135. ZHAO Kuan, CHEN Jianjun, CAO Hongjun, et al.Randomness analysis of dynamic responses of a slider-crank system with clearances[J]. Journal of Vibration and Shock, 2014, 33(11): 130-135.

[19] OLYAEI A A, GHAZAVI M R. Stabilizing slider-crank mechanism with clearance joints[J]. Mechanism and Machine Theory, 2012, 53(3): 17-29.

[20] 王威, 沈政, 宋玉玲, 等. 含间隙和干摩擦的连杆机构系统动力学研究[J]. 振动与冲击, 2015, 34(18): 210-214. WANG Wei, SHEN Zheng, SONG Yuling. System dynamics of linkage mechanism with clearance and dry friction[J]. Journal of Vibration and Shock, 2015, 34(18): 210-214.

[21] HOU Yulei, ZENG Daxing, ZHANG Zhanye, et al. A novel two degrees of freedom rotational decoupled parallel mechanism[J]. Applied Mechanics and Materials, 2012, 215/216: 293-296.

[22] LANKARANI H M, NIKRAVESH P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207.

[23] FLORES P, AMBRSIO J, CLARO J C P, et al. Influence of the contact—Impact force model on the dynamic response of multi-body systems[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2006, 220(1): 21-34.

[25] FLORES P, AMBRSIO J. On the contact detection for contact-impact analysis in multibody systems[J]. Multibody System Dynamics, 2010, 24(5): 103-122.

Chaos andimpact phenomena of a RU-RPR decoupled parallel mechanism containing clearance

HOU Yulei1, WANG Yi1, JING Guoning1, ZENG Daxing1, QIU Xuesong1, LI Huijian2

(1. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;2. Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures of Hebei Province, Yanshan University, Qinhuangdao 066004, China)

For chaos and impact phenomena in a mechanism with clearance, taking a two-rotation decoupled parallel mechanism RU-RPR (R stands for a revolute pair, U stands for a Hooke joint, P stands for a translation pair) proposed independently as a study object, considering clearance existing in a kinematic pair, combining with Lankarani-Nikravesh contact force model and Lagrange equation, the dynamic equation of the mechanism was established, and its chaos and impact phenomena were studied. Then the influences of different driving speeds and friction coefficients on chaos and impact phenomena were analyzed, and the relationship between the stability of the mechanism and impact phenomenon was investigated at the same time. The influences of an additional spring on dynamic characteristics of the mechanism were analyzed. The results showed that when changing drive speed or friction coefficient, the impact phenomenon still exists, while the motion of the mechanism can be changed from chaotic motion to periodic one, the stability of the mechanism is enhanced; there is no necessary relation between the stability of the mechanism and its impact phenomenon, and the impact level can be significantly weakened by adding springs.

parallel mechanism; clearance; dynamics; chaos; impact

国家自然科学基金(51205339;51305384)；中国博士后科学基金(2013M541199)

2015-08-16 修改稿收到日期：2015-12-30

侯雨雷 男，博士后，教授，博士生导师，1980年生

李慧剑 男，博士，教授，博士生导师，1980年生

TH113

A

10.13465/j.cnki.jvs.2017.01.032