多排环境下转子叶片气动弹性稳定性机理分析

杨 慧， 李振鹏

(北京航空航天大学 能源与动力工程学院, 先进航空发动机协同创新中心，北京 100191)

多排环境下转子叶片气动弹性稳定性机理分析

杨 慧， 李振鹏

(北京航空航天大学 能源与动力工程学院, 先进航空发动机协同创新中心，北京 100191)

传统叶片颤振分析多是基于单转子研究模型，发动机的紧凑性要求导致级间距减小，多排耦合作用对颤振的影响将不容忽视。采用自行开发的程序对某型1.5级高压压气机进行了流固耦合数值模拟，分析上、下游叶排对转子叶片颤振特性的影响。针对典型工况，分别进行了单转子模型，导叶转子模型，转子静子模型，导叶转子静子模型的叶片气动弹性稳定性分析。研究表明，激波振荡对颤振特性影响显著；多排环境下存在非定常压力波的反射和叠加，明显改变转子叶片表面的非定常压力幅值和相位，进而改变转子叶片气动弹性稳定性。多排干涉作用提高了转子叶片的气动阻尼，尤其是上、下游叶排同时作用时阻尼提高了近732.7%。

颤振；全环多排；流固耦合；气动阻尼；压力波

颤振是叶轮机械叶片振动的一种，严重制约着发动机的结构完整性和可靠性[1]。当今对高推重比的追求[2]与轻薄叶片的使用使得叶片颤振问题越发剧烈，并成为设计人员不得不攻克的技术难题。颤振是流体诱导叶片振动的一种，涉及复杂的流固耦合作用，因其多发性及灾难性，吸引了众多学者对其进行深入研究。

准确分析叶片颤振问题需要求解非定常流场和结构动力学方程，为了节省数值模拟时间，达到工程应用的要求，需要根据特定的问题，使用简化的数值模型和缩减的空间模型以减少求解方程的时间。SRIVASTAVA等[3]使用单通道模型施加相移边界条件，进行了正激波对叶片颤振影响的无粘分析，指出激波对叶片气弹的稳定作用或失稳作用与激波位置、叶片间相位角(InterBlade Phase Angle, IBPA)和振动频率有关。VASANTHAKUMAR[4]使用频域线化法，在单通道模型上施加相移边条，指出激波位置及运动，以及激波与IBPA的关系对叶片气动阻尼影响显著，振动模态是重要的影响因素之一。但使用小扰动假设的线化方法分析非定常流场，不能很好地解决激波、分离流等强非线性问题。

ISOMURA等[5]采用准三维的粘性非定常CFD程序，在单叶片模型上证明了激波振荡而非叶片失速是跨音速风扇颤振失稳的主要原因。张小伟等[6-7]采用能量法发现叶片间相位角和振动模态对叶片颤振有关键性影响。这些基于能量法的气动弹性模型，不能考虑颤振问题中流体对固体的作用，也无法真实地捕捉流场的非定常流动特征。IM等[8]通过流固耦合方法，在半环叶排模型上研究发现脱体激波和叶尖间隙泄漏涡及吸力面附面层的非定常流动干扰作用是高负荷跨音速风扇颤振失稳的主要原因。这些基于单转子模型的研究成果，主要考虑同排叶片间的气动耦合作用。

发动机紧凑型的设计要求导致叶轮机部件转、静子间距越来越小，转静干涉作用明显增强。目前多排干涉作用的研究重点在于其对气动性能、非定常效应以及时序效应的影响[9-11]，而多排叶片间的气动耦合作用是否会对叶片气动弹性稳定性产生明显作用，其影响机理如何，以及如何有效的预测多排环境中的颤振问题，都需要深入研究。BUFFUM等[12-14]使用频域法，在二维单通道模型上，采用耦合模态方法首先分析了多排间的耦合作用。研究表明在多排干涉作用下，气动阻尼与孤立振荡叶栅显著不同，转静轴向间距是关键参数。LI等[15]采用频域法，在三维单通道模型上研究了轴向间距对转子叶片气动阻尼的影响。在特定间距值下，静子的干涉作用会使转子叶片的气动阻尼增长100%，且叶片气动阻尼和间距的关系与静子叶片数有关，并存在一个可以显著改善颤振和强迫响应问题的最佳间距值。HSU等[16]为了考察使用多排模型和复杂气动弹性模型的必要性，对比了全环多排流固耦合法和传统单排单通道能量法的颤振特性计算结果，发现单排单通道模型不能正确预测颤振发生，而全环多排模型的预测结果和实验一致。

综上可知，转静干涉作用对多排环境中的叶片颤振特性产生明显影响，其影响机理需要深入研究。只有采用全环多排模型才能精确预测多排效应对叶片颤振的影响以及非定常压力波在各个方向上的变化；考虑流固耦合作用才能真实地捕捉流场的非定常流动特征，特别是跨音速工况下。本文采用全环多排模型的流固耦合算法进行叶片颤振特性分析。针对典型气动工况，通过单转子模型，导叶-转子模型，转子-静子模型，导叶-转子-静子模型的颤振特性结果对比，研究多排干涉作用对转子叶片气弹稳定性的影响，为更深入地理解多排环境中叶片颤振发作机理提供参考。

1 数值方法

本文采用自行开发的流固耦合分析程序HGAE，通过叶片在非定常流场中随时间的位移变化历程来判断叶片的气动弹性稳定性。

流体域求解动边界和动态变形网格下的守恒型积分形式的三维非定常可压缩雷诺平均Navier-Stokes方程，其方程为：

(1)

叶片的动力学方程通过广义坐标解耦，得到N个线性无关的常微分方程组：

(2)

模态位移向量ζ与物理位移向量x的关系为

x=Φζ

(3)

式中：Φ为质量归一化的系统振型矩阵，由单叶片振型组集[18]而来。通过迭代求解方程(1)和方程(2)，得到每一时间步的流场参数及叶片位移，从而得到模态位移随时间变化的历程。

采用指数函数曲线拟合模态位移曲线，计算各阶模态的气动阻尼，判定叶片的气动弹性稳定性，该流固耦合求解方法针对全环模型可同时考虑多个振动模态和所有叶片间相位角，详细的数值方法介绍见参考文献 [18-19] ，其在气动弹性领域的有效性验证见文献[17,20]。

2 计算说明

本文采用某型高压压气机前1.5级，算例的基本参数见表1。

表1 基本参数

图1(左)为导叶-转子-静子模型的全环网格，其拓扑结构均为O4H型。导叶的全环网格节点数约为780×104；转子的全环网格节点数约为580×104，静子的全环网格节点数约为523×104。第1层网格距壁面厚度均为0.01 mm。图1(右)为转子叶片的有限元网格，采用八节点六面体单元，根部固支，网格数为24×2×20。

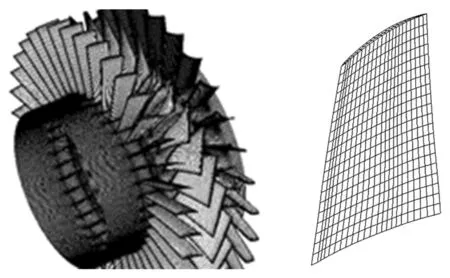
图1 导叶-转子-静子模型网格(左)和叶片有限元网格(右)Fig.1 Grids of IGV-rotor-stator(left)and blade FEM grids (right)

为确定叶片气动弹性分析的工况点，通过1.5级模型完成特性计算。进口给定总压101 325 Pa，总温288.15 K，轴向进气，出口给定轮毂处静压并结合径向压力平衡方程，转静交界面使用混合面[21]方法。非定常流动计算时，转静交界面使用双线性插值的滑移面[22]方法。

颤振计算工况选取近设计点，流场较为“干净”，便于分析上、下游叶排的干涉作用对转子叶片气动弹性稳定性的影响。分别针对单转子模型，导叶-转子模型，转子-静子模型，导叶-转子-静子模型进行颤振特性分析，各模型的边界条件由特性计算时交界面的参数分布给出，从而保证各个模型下计算流量以及叶表的定常气动负荷一致，进而实现计算工况一致。

叶片颤振计算在全环定常流动结果上给定叶片微小的模态速度以激励叶片初始振动。为了简化分析，计算中仅考虑叶片的1阶弯曲振动模态，包含所有行波节径(如28个叶片对应28个行波节径，分别为0，1，-1，2，-2，…，13，-13，14)。计算物理时间步长取为叶片振动周期的1/100，共计算了20个周期。

3 计算结果

3.1 气动阻尼计算结果

图2所示为四种模型下转子叶片气动阻尼随节径的变化。对于单转子模型，气动阻尼随节径正弦规律变化，节径对气动阻尼影响显著。这与文献[4]和文献[20]的计算结果一致。气动弹性最不稳定状态(最小值)对应前行波1节径，气动阻尼为负，叶片气动弹性失稳。

导叶没有使最危险节径发生变化，下游静子的作用使得最危险节径由1变为0，上下游叶排同时存在时，危险节径由1变为0。由图可知，叶排干涉作用使得气动阻尼随节径振荡变化，在单转子正弦规律下呈现多峰值现象，增加或降低了单转子的气动阻尼值。表明非定常压力波沿叶排周向的传播受节径的影响，如果使用单通道模型必须遍历所有的节径，才能获得正确的结果。

图2 不同模型下气动阻尼对比Fig.2 Aerodynamic damping comparision under different models

图3所示为不同模型的最小气动阻尼值对比，由图可知，导叶使得转子最危险节径下的气动阻尼增加了174.8%，下游静子使其提高近327.8%，上下游叶排同时存在时，最小气动阻尼提高近732.7%。在本文选取的级间距值下，多排环境显著提高了最不稳定状态下转子叶片的气弹稳定性，尤其是上下游叶排同时存在的情况下，并且下游静子对气弹稳定性的影响大于上游导叶。

图3 最小气动阻尼对比 Fig.3 Minimum aerodynamic damping comparison

3.2 单转子模型结果分析

图4为85%叶高和叶尖区域的流场Ma分布。由图可知，在转子通道中，存在一道较强的脱体激波，与吸力面相交于50%弦长处；在叶尖区域，泄漏涡与激波相互作用，引起局部气流堵塞。

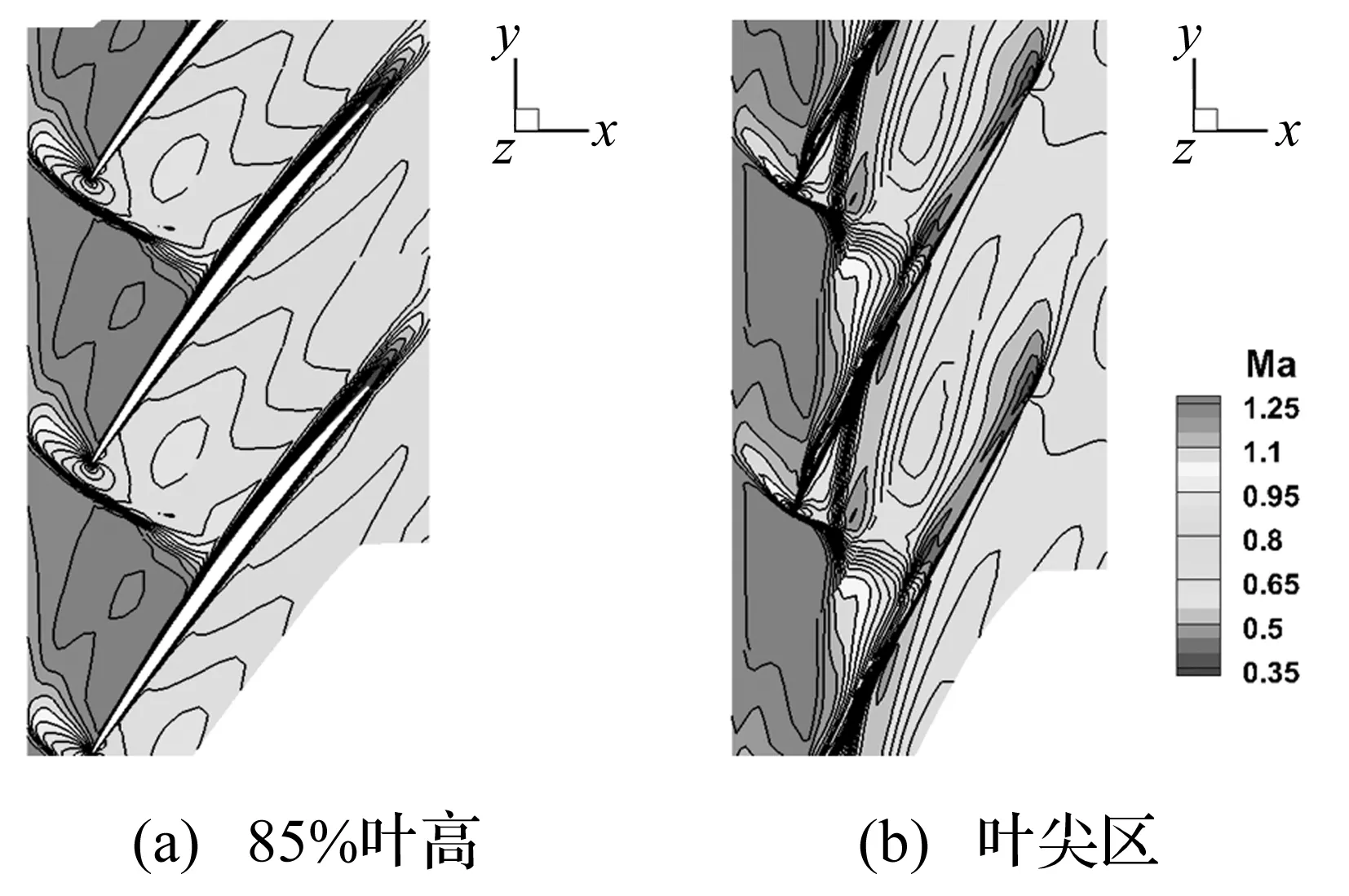
图4 流场Ma云图(85%叶高)Fig.4 Ma contour of Flow field (85% span)

图5为非定常压力的时空分布图，非定常压力定义为在叶片一个振动周期内，瞬时压力和平均压力之差。

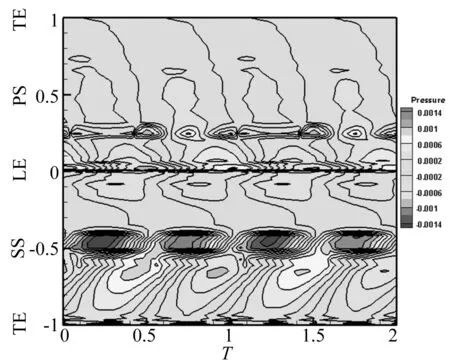
图5 非定常压力时空分布(单转子，85%叶高)Fig.5 Time-space distribution of unsteady pressure(single rotor, 85% span)

由图5可知，吸力面(SS)非定常压力强于压力面(PS)，在转子叶片吸力面50%弦长处存在激波附面层干扰现象，激波振荡是引起叶表非定常压力的主要原因。

叶尖位置叶片振动幅值最大，引起的能量转换也最剧烈，对叶片气弹稳定性影响明显，而本文脱体激波与叶尖泄漏涡在此处又存在干涉作用(如图4(b))。分析叶尖区域A点(激波附近)、B点和C点(叶尖其他区域)的非定常压力和叶片位移的相位关系(如图6)可知，激波附近A点的压力和叶片位移反相变化，表明激波对气弹稳定性起稳定作用[23]；而在叶尖其他区域(B点和C点)压力和叶片位移相位近似同相变化，产生气弹失稳效应。由此推断在本文算例中，激波振荡通过改变转子叶尖非定常压力的相位，对气动弹性起到一定稳定作用

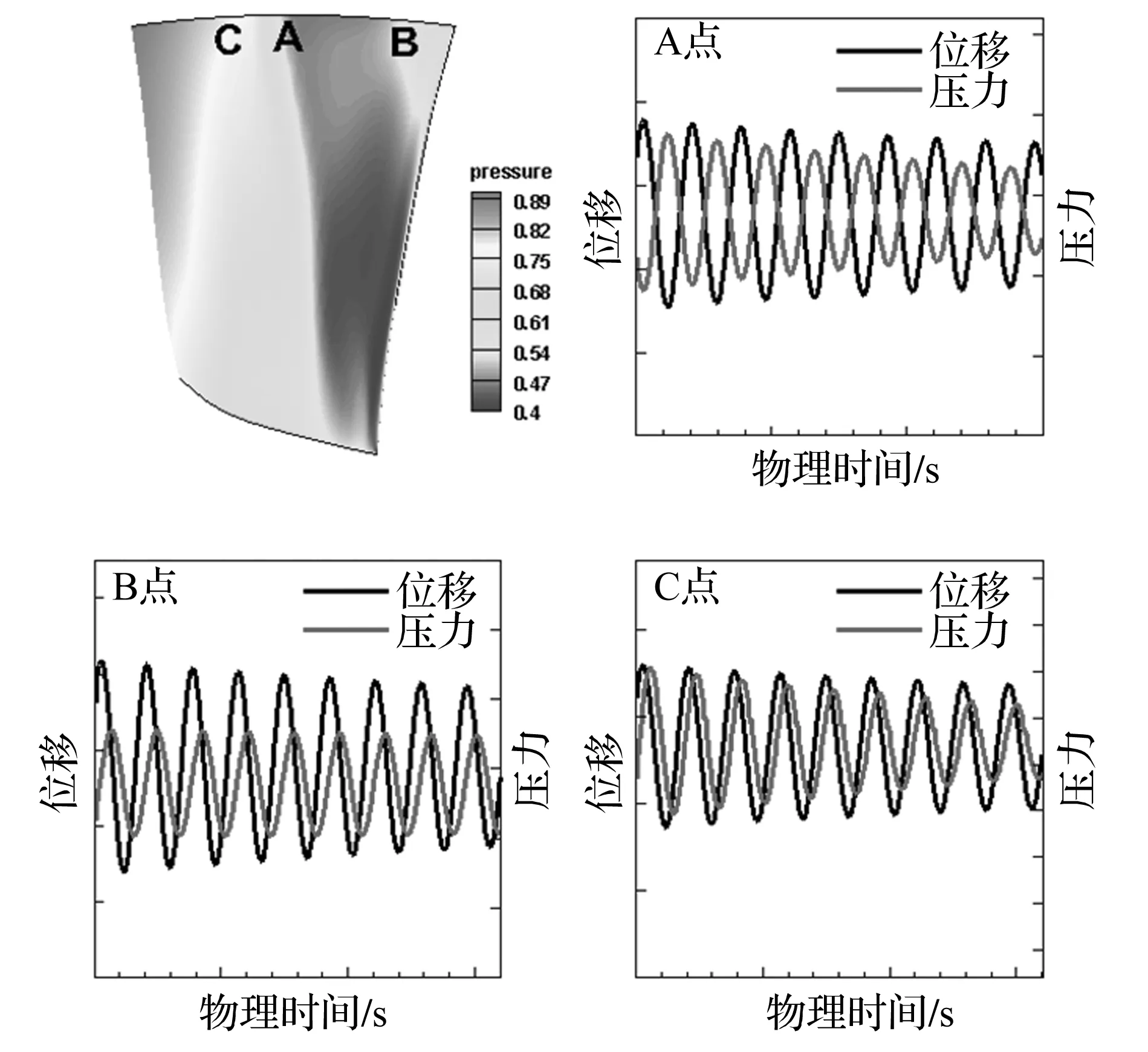
图6 转子吸力面压力云图及点A、B、C的压力和位移时间历程Fig.6 Pressure contour on rotor suction surface and time histories of pressure and displacement at point A, B and C

3.3 导叶-转子模型结果分析

图7为上游导叶轴向力的频谱分析，由图可知，多排环境下导叶上的扰动频率主要为叶片振动频率和转子通过频率，在上游导叶中，振动频率的作用甚至高于通过频率。可见下游转子叶片振动引起的非定常压力波向上游传播，作用在前排导叶上。图8为转子叶片吸力面非定常压力幅值和相位，通过单转子模型和导叶-转子模型的叶表非定常压力对比可知，导叶-转子模型激波前非定常高压力幅值区域沿径向扩展到近50%叶高，且叶尖前缘高幅值范围也变大；激波前的相位产生近似180°的变化，激波对导叶-转子模型的颤振稳定性作用明显。结果表明导叶将转子叶片振动产生的压力扰动波反射回转子表面，并与转子叶片上的非定常压力波叠加。文献[23]研究表明，反射波与叶表压力扰动波的叠加情况由两者之间的相位差决定，而此相位差受转子叶片的振动节径影响。图2中气动阻尼值随节径的变化规律，验证了文献[23]的这一结论。

图7 导叶轴向力(Fx)频谱分析Fig.7 Frequency spectrum of axial force (Fx) on IGV

图8 转子叶片非定常压力幅值及相位(吸力面，振动频率)Fig.8Unsteady pressure amplitude and phase on rotor blade (suction surface, vibration frequency)

为了分析叶片振动对流场的影响，针对导叶-转子模型分别进行了非定常流动计算和叶片振动的颤振特性计算。图9列出了转子叶片85%叶高处叶表非定常压力的时空分布图。非定常流动计算时，势干扰作用引起叶片前缘剧烈的压力脉动，流场呈现周期性变化；当考虑叶片振动的气动弹性稳定性分析时，叶片的衰减振动导致流场势干扰引起的周期性变化明显减弱，表现为压力脉动的幅值明显降低。而在吸力面50%弦长处出现了激波振荡引起的周期性变化。

图10为两种计算条件下导叶和转子叶片85%叶高处通过频率下的非定常压力幅值对比。可见叶片的振动作用显著降低了上下游通过频率下叶表非定常压力幅值。多排环境中，叶片振动会对强迫响应产生影响。

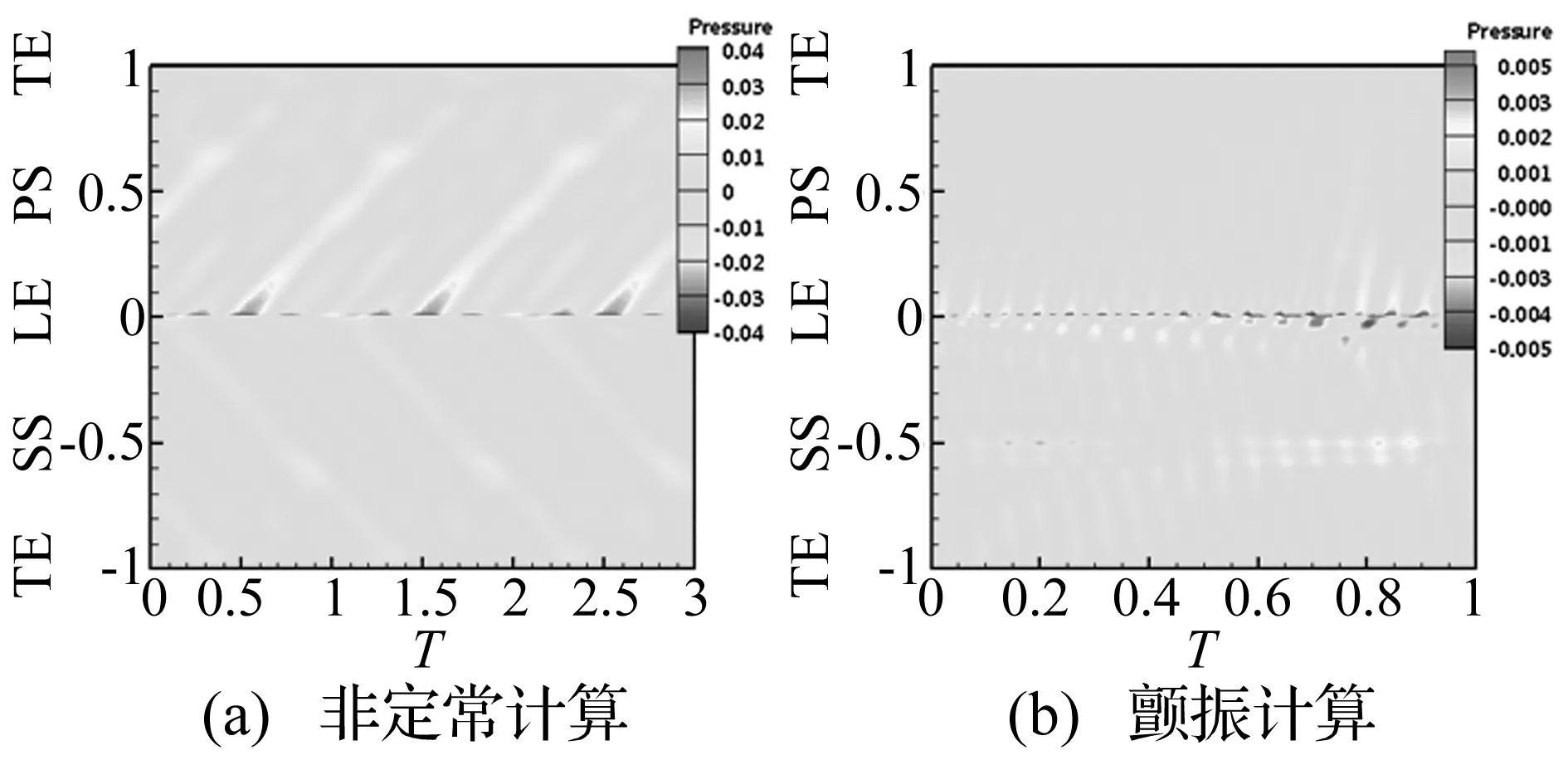
图9 转子叶表非定常压力时空分布(导叶转子，85%叶高)Fig.9 Time-space distribution of unsteady pressure on rotor surface (IGV-rotor, 85% span)

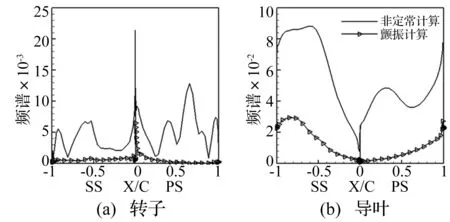
图10 两种计算下非定常压力幅值对比(85%叶高，通过频率)Fig.10 Comparison of two calculated amplitudes of unsteady pressure (85% span, blade passing frequency)

3.4 转子-静子模型结果分析

图11为转子-静子模型中叶片表面振动频率下非定常压力幅值和相位。与单转子(图8(a))结果对比，激波后高幅值范围增加了约20%弦长，且在尾缘和叶尖前缘区域幅值均增加；叶尖尾缘大面积区域相位发生近120°变化，激波后50%叶高以下相位发生了180°转变。这些变化使得转子叶片最小气动阻尼提高(图3)，且最危险节径发生改变(图2)。

图11 转子叶片压力幅值及相位(转子-静子模型，吸力面，振动频率)Fig.11 Unsteady pressure amplitude and phase on rotor blade (rotor-stator, suc.sur, vibration freq.)

如图12所示，在静子叶片尾缘处存在大面积分离，分离频率约为1 516 Hz(如图12(b))。周期性分离是流场主要的扰动源，由图13中轴向力的频谱分析可知，即使在转子域中，流场分离仍是主要扰动源，振动频率和通过频率的作用十分微小。在静子域中并没有振动频率的作用，表明流场的大分离影响了压力扰动波的传播。下游静子大分离流场对压力波反射的影响改变了多排环境下叶片气弹稳定性。

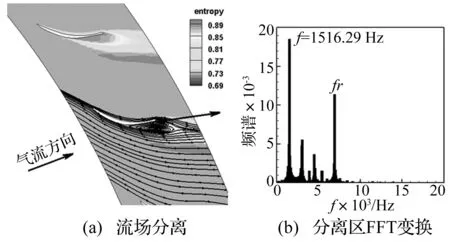
图12 静子流场分离区(85%叶高)Fig.12 Separation flow in the flow field of stator

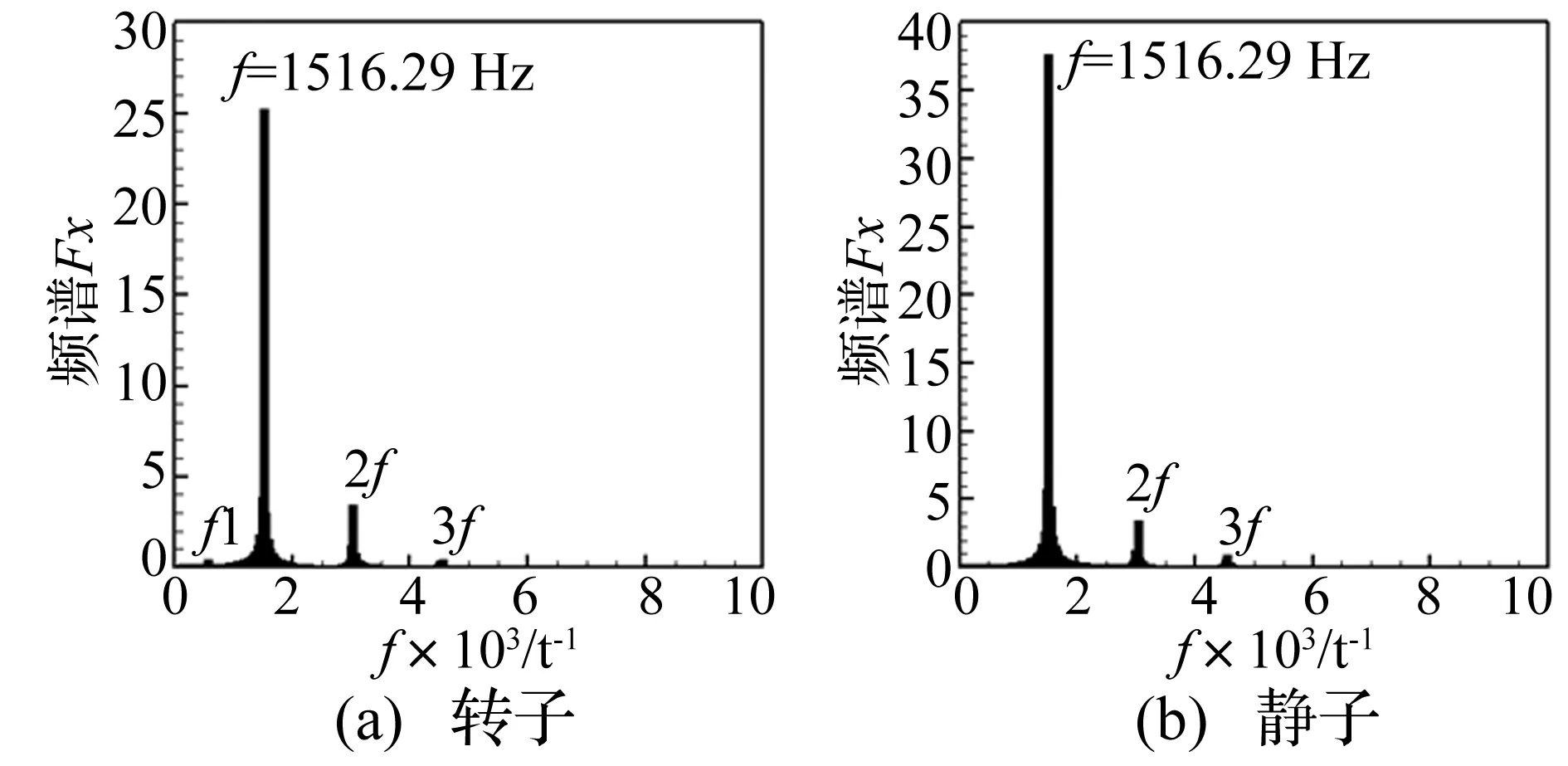
图13 轴向力(Fx)频谱分析Fig.13 Frequency spectrum of axial force (Fx)

3.5 导叶-转子-静子模型结果分析

导叶-转子-静子模型的转子叶表非定常压力幅值和相位如图14所示。与单转子模型(图8(a))对比，叶表激波位置，前缘和尾缘压力幅值均增加明显，多排的耦合作用剧烈；在激波振荡位置及激波前大面积区域相位接近0°，使得原来叶尖前缘及激波处的相位发生了近180°变化，在激波后靠近尾缘大面积区域相位同样发生了近180°变化。从整体上看，导叶-转子-静子模型的转子叶表非定常压力幅值和相位近似为导叶-转子和转子-静子两种模型的耦合效果，导致转子叶片最小气动阻尼较单转子模型大幅提高(图3)。

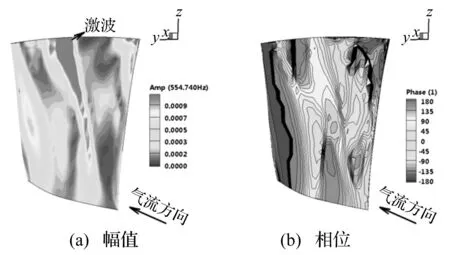
图14 转子叶片压力幅值及相位(导叶-转子-静子模型，吸力面，振动频率)Fig.14 Unsteady pressure amplitude and phase on rotor blade (IGV-rotor-stator, suc.sur., vibration freq.)

4 结 论

本文采用自行开发的流固耦合程序详细分析了多排耦合作用对转子叶片颤振特性的影响。研究了上游导叶、下游静子及上下游叶排同时存在时对转子叶片一阶弯曲模态气动弹性稳定性的影响机理，有如下结论：

(1)对于单转子模型，激波振荡是叶表非定常压力的主要原因；其通过改变叶尖非定常压力的相位，对叶片气动弹性起到一定稳定作用。

(2)叶片振动作用，将导致上下游叶排通过频率下的非定常压力幅值降低。

(3)多叶排环境下，导叶、静子作用使得转子叶表非定常压力波反射，显著改变转子叶表非定常压力的幅值和相位，使得气动阻尼随节径呈现多峰值振荡现象。本文算例中，多排的干涉作用明显改善了叶片一阶弯曲振动最不稳定状态的气弹稳定性，下游静子的作用大于上游导叶。

(4)由本文研究结果可以推断，使用单转子模型分析转子叶片的气动弹性稳定性将得到不准确的预测结果，特别是跨音速工况下，同时存在复杂的分离流动和叶尖间隙涡的情况。

(5)本算例中，单转子模型给出过保守的气动弹性稳定性预测。下游静子的周期性分离流动会影响非定常压力波的反射，其影响机制需要进一步深入研究。

[ 1 ] SRINIVASAN A V. Flutter and resonant vibration characteristics of engine blades[J]. Journal of Engineering for Gas Turbines and Power, 1997, 119(4): 742-775.

[ 2 ] 陈懋章. 风扇/压气机技术发展和对今后工作的建议[J]. 航空动力学报, 2002, 17(1): 1-15. CHEN Maozhang. Development of fan/compressor techniques and suggestions on further researches[J]. Journal of Aerospace Power,2002,17(1):1-15.

[ 3 ] SRIVASTAVA R, KEITH T G. Shock induced flutter of turbomachinery blade row[C]//ASME Turbo Expo 2004: Power for Land, Sea, and Air.American Society of Mechanical Engineers, 2004:487-496.

[ 4 ] VASANTHAKUMAR P. Computation of aerodynamic damping for flutter analysis of a transonic fan[C]//ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. American Society of Mechanical Engineers, 2011:1429-1437.

[ 5 ] ISOMURA K, GILES M B. A numerical study of flutter in a transonic fan[J]. Journal of Turbomachinery,1998,120(3): 500-507.

[ 6 ] 张小伟,王延荣,许可宁.叶轮机械叶片颤振的影响参数[J].航空动力学报, 2011,26(7):1557-1561. ZHANG Xiaowei,WANG Yanrong,XU Kening.Effects of parameters on blade flutter in turbomachinery [J].Journal of Aerospace Power, 2011, 26(7):1557-1561.

[ 7 ] 张小伟,王延荣.叶片间相位角对叶片颤振的影响[J].航空动力学报, 2010,25(2):412-416. ZHANG Xiaowei,WANG Yanrong.Influence of interblade phase angle on the flutter of rotor blades[J].Journal of Aerospace Power, 2010, 25(2):412-416.

[ 8 ] IM H S, ZHA G C.Flutter prediction of a transonic fan with travelling wave using fully coupled fluid/structure interaction[C]//ASME Turbo Expo 2013:Turbine Technical Conference and Exposition. American Society of Mechanical Engineers,2013.V07BT33A003.

[ 9 ] SUN Y, REN Y X,FU S,et al. The influence of rotor-stator spacing on the loss in one-stage transonic compressor[C]//ASME Turbo Expo 2009: Power for land, Sea and Air . American Society of Mechanical Engineers, 2009：1707-1715.

[10] NG W F, OBRIEN W F, OLSEN T L. Experimental investigation of unsteady fan flow interaction with downstream struts[J]. Journal of Propulsion and Power, 1987, 3(2): 157-163.

[11] SAREN V E, SAVIN N M, DORNEY D J, et al. Experimental and numerical investigation of airfoil clocking and inner-blade-row gap effects on axial compressor performance [J]. International Journal of Turbo and Jet Engines, 1998(15): 235-252.

[12] BUFFURN D H. Blade row interaction effects on flutter and forced response[J]. Journal of Propulsion and Power, 1995, 11(2): 205-212.

[13] HALL K C, SILKOWSKI P D.The influence of neighboring blade rows on the unsteady aerodynamic response of cascades[J]. Journal of Turbomachinery, 1997(119):85-93.

[14] SILKOWSKI P D, HALL K C. A coupled mode analysis of unsteady multistage flows in turbomachinery[J]. Journal of Turbomachinery,1998(120): 410-421.

[15] LI H D,HE L.Blade aerodynamic damping variation with rotor-stator gap:A computational study using single-passage approach[J]. Journal of Turbomachinery, 2005,127(3): 573-579.

[16] HSU K,HOYNIAK D,ANAND M S.Full-annulus multi-row flutter analyses[C]//ASME Turbo Expo 2012: Turbine Technical Conference and Exposition.American Society of Mechanical Engineers, 2012:1453-1462.

[17] 郑赟.基于非结构网格的气动弹性数值方法研究[J]. 航空动力学报, 2009,24(9):2069-2077. ZHENG Yun.Computational aeroelasticity with an unstructured grid method[J].Journal of Aerospace Power, 2009, 24(9): 2069-2077.

[18] 张锦,刘晓平.叶轮机振动模态分析理论及数值方法[M].北京:国防工业出版社, 2001.

[19] 郑赟,杨慧.跨音速风扇全环叶片颤振特性的流固耦合分析[J].北京航空航天大学学报,2013,39(5):626-630. ZHENG Yun,YANG Hui.Full assembly fluid/structured flutter analysis of a transonic fan[J].Journal of Beijing University of Aeronautics and Astronautics, 2013,39(5):626-630.

[20] ZHENG Yun, YANG Hui. Coupled fluid-structure flutter analysis of a transonic fan[J]. Chinese Journal of Aeronautics, 2011, 24(3): 258-264.

[21] CHIMA R V.Calculation of multistage turbomachinery using steady characteristic boundary conditions[R].Reston,VA:36th Aerospace Sciences Meeting &Exhibit,1998.

[22] MATHUR S R.Unsteady flow simulations using unstruck tured sliding meshes[R]. Reston, VA:25th AIAA Fluid Dynamics Conference, 1994.

[23] VAHDATI M, SIMPSON G, IMTEGUN M.Mechanisms for wide-chord fan blade flutter[J]. Journal of Turbomachinery, 2011, 133(4): 1396-1402.

Aeroelastic stability analysis of rotor blades under multi-row environment

YANG Hui, LI Zhenpeng

(Collaborative Innovation Center for Advanced Aero-Engine，School of Energy and Power Engineering, Beihang University, Beijing 100191, China)

Conventional blade flutter analysis is normally based on an isolated blade row model, the influence of multi-row aerodynamic coupling on blade flutter characteristics can’t be ignored when rotor-stator gaps decrease due to aeroengine compact requirements. A fluid-structure coupled simulation for a 1.5stage HPC was conducted with a self-developed algorithm to analyze the influence of upstream and downstream blade rows on rotor blade flutter characteristics. Aiming at a typical operation condition, rotor blades’ aeroelastic stability analyses were performed with an isolated rotor model, an IGV-rotor model, a rotor-stator one and an IGV-rotor-stator one, respectively. The results showed that the shock wave vibration influences the flutter stability significantly; there are reflection and superposition of unsteady pressure waves under the multi-row environment, the amplitude and phase of unsteady pressures on the rotor blade surface are changed obviously and furthermore the blade aeroelastic stability is changed; multi-row interferences raise the aerodynamic damping of rotor blade, especially, when the upstream and downstream blade rows act simultaneously, the damping value increases by nearly 732.7%.

blade flutter; full-annulus/multi-row; fluid-structure interaction; aerodynamic damping; pressure wave

2015-07-10 修改稿收到日期：2015-12-29

杨慧 女，博士，讲师，1970年10月生

V232.4

A

10.13465/j.cnki.jvs.2017.01.022