基于分步无电离层组合的北斗三频长距离参考站间宽巷模糊度解算方法
2017-02-09高成发潘树国乔龙雷
高 旺 高成发 潘树国 乔龙雷 赵 庆
(1东南大学交通学院, 南京 210096)(2东南大学仪器科学与工程学院, 南京 210096)
基于分步无电离层组合的北斗三频长距离参考站间宽巷模糊度解算方法
高 旺1高成发1潘树国2乔龙雷1赵 庆1
(1东南大学交通学院, 南京 210096)(2东南大学仪器科学与工程学院, 南京 210096)
针对北斗三频长距离参考站间宽巷(含超宽巷)模糊度解算中存在的问题,分析了影响宽巷组合(WLC)法、载波伪距组合的无几何无电离层(GIF)法及分步无几何(TCAR)法的主要因素及各自的局限性.在此基础上,基于参考站间基线已知的特性,提出了一种分步解算的无电离层(SIF)方法.首先采用载波伪距组合求解(0,-1,1)超宽巷模糊度,利用模糊度已固定的(0,-1,1)载波观测值与第2个宽巷/超宽巷观测值组成载波无电离层组合,同时分析了残余几何项误差对模糊度解算的影响.最后采用了一组长度为265 km的实测北斗三频基线数据进行了实验验证.实验结果表明,所提SIF方法能够有效消除长基线情况下电离层延迟的影响,同时受观测值噪声的影响较小.
北斗;三频;宽巷模糊度;长基线;电离层延迟
网络RTK(real time kinematic)技术是目前应用范围最广的卫星精密定位技术,它能够让用户便捷地在较大空间范围内实时地获得均匀、高精度、可靠的定位结果,已广泛应用于测绘、精密导航等领域[1-3].近年来随着卫星定位技术的发展,长基线网络RTK成为发展的热点和趋势,而参考站间的模糊度快速准确解算则是这一技术的核心问题.目前双频网络RTK模糊度求解常用三步法[4]:① 利用宽巷组合的长波特性,采用几何无关组合确定宽巷模糊度;② 利用电离层无关组合同步估计对流层天顶延迟湿分量和基频模糊度浮点解及其方差协方差矩阵;③ 通过整数搜索方法求取基频模糊度固定解.在这一过程中,宽巷模糊度的快速准确求解是整个算法的前提和保障.
目前双频宽巷模糊度求解的常用方法有双频P码与相位观测值线性组合法(MW方法)和宽巷组合法(WLC法)[5],但MW法受伪距观测值噪声影响较大,特别是对于双差伪距观测误差在一定时间内不符合白噪声特性时,MW方法解算成功率较低;而WLC方法无法削弱双差电离层的影响而使基线距离受限.多频信号可以构成具有诸多优点的观测值组合,能够有效改正大气误差,提高模糊度的固定效率,因此成为卫星定位领域的研究热点.利用多频观测值求解宽巷(含超宽巷)模糊度,国内外学者相继提出了一系列方法,典型的如分步无几何(TCAR)方法[6]、无几何无电离层(GIF)方法[7]等.但上述方法多是针对常规基线模式,没有充分利用网络RTK基线分量精确已知的特性,在受大气误差和观测值噪声影响方面有待进一步提高.
我国的北斗卫星系统全部卫星均支持播发三频信号,充分发挥北斗的三频优势,更好地促进网络RTK等高精度定位方法的应用,成为北斗系统推广应用的一项重要内容.本文针对北斗三频,对比分析在不同大气延迟和观测值噪声情况下几种常用宽巷模糊度求解方法的表现性能,指出了影响每种方法求解精度的主要因素,同时提出了一种适用于网络RTK的载波无电离层宽巷解算方法,并通过一组265 km的长基线数据进行实验验证.
1 北斗观测值及其线性组合
考虑双差对流层和电离层一阶项的影响,以距离为单位的北斗双差载波和伪距观测方程可分别表示为[8-9]
Δφ(i,j,k)=Δρ+ΔT-η(i,j,k)ΔI+
λ(i,j,k)ΔN(i,j,k)+Δεφ(i,j,k)
(1)
ΔP[α,β,γ]=(α+β+γ)(Δρ+ΔT)+
η[α,β,γ]ΔI+ΔεP[α,β,γ]
(2)
其中组合的双差载波和伪距观测值为
(3)
ΔP[α,β,γ]=αΔP1+βΔP2+γΔP3
(4)
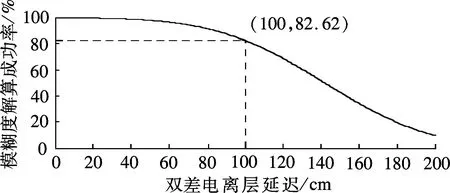
式中,Δφ(i,j,k)和ΔP[α,β,γ]分别为组合的载波和伪距观测值;i,j,k为任意整数; Δφm为第m(m=1,2,3)个频率上的双差载波观测值;α,β,γ为任意实数;ΔPm为第m个频率上的双差伪距观测值;f1,f2,f3分别为北斗系统的3个载波频率;Δρ,ΔT和ΔI分别为双差站星距离、双差对流层延迟值、北斗频点1上的双差电离层延迟值;λ,ΔN(i,j,k)分别为组合观测值的波长和模糊度;η(i,j,k),η[α,β,γ]分别为组合双差载波、伪距观测值的电离层延迟因子;Δεφ(i,j,k)和ΔεP[α,β,γ]分别为组合双差载波、伪距观测值的噪声[8-9].一般认为3个频点上的载波观测值等精度,即σΔφ1=σΔφ2=σΔφ3=σΔφ,则组合载波观测值的精度为
μ(i,j,k)σΔφ
(5)
式中,f(i,j,k)为组合观测值的频率;μ(i,j,k)为组合载波观测值噪声放大因子.对于北斗3个频点的伪距观测值P1,P2和P3,由于第3个频点的码率高于第1和第2个频点码率,因此一般认为P3精度高于P1和P2[10].假设q1和q2分别为P2,P3相对P1的噪声比值,则组合伪距观测值的精度为
(6)
利用3个频点的载波观测值进行组合,可构建出一系列具有长波长的宽巷或超宽巷组合,典型的组合如表1所示[3,8,10].
2 宽巷模糊度解算方法
2.1 现有三频宽巷模糊度解算方法
针对网络RTK,现有的三频宽巷模糊度解算方法可主要归纳为三频宽巷组合定义法(WLC)、三频载波伪距组合的无几何无电离层(GIF)、分步无几何(TCAR)3种方法.
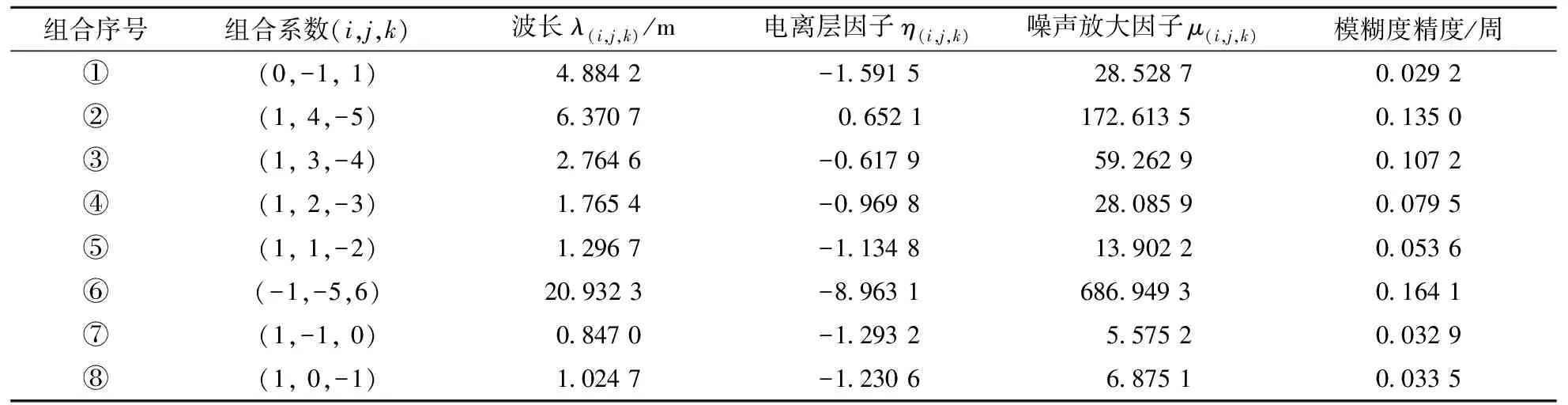
表1 北斗宽巷/超宽巷载波组合(σΔφ=0.5 cm)
2.1.1 三频宽巷组合定义法
考虑网络RTK参考站坐标已知,结合式(1),三频宽巷组合定义法可表示为
(7)
从式(7)中可以看出,影响宽巷、超宽巷模糊度解算成功率的主要因素为双差对流层和电离层延迟值.由于对流层和电离层误差为非白噪声误差,因此会造成模糊度解算的系统性偏差.取基础的双差载波观测值精度σΔφ=0.5 cm,针对不同基线长,分析模糊度解算成功率与未模型化双差大气误差(即ΔT/η(i,j,k)-ΔI的等效误差)之间的关系,如图1所示,其中模糊度解算成功率采用下式进行计算[11]:
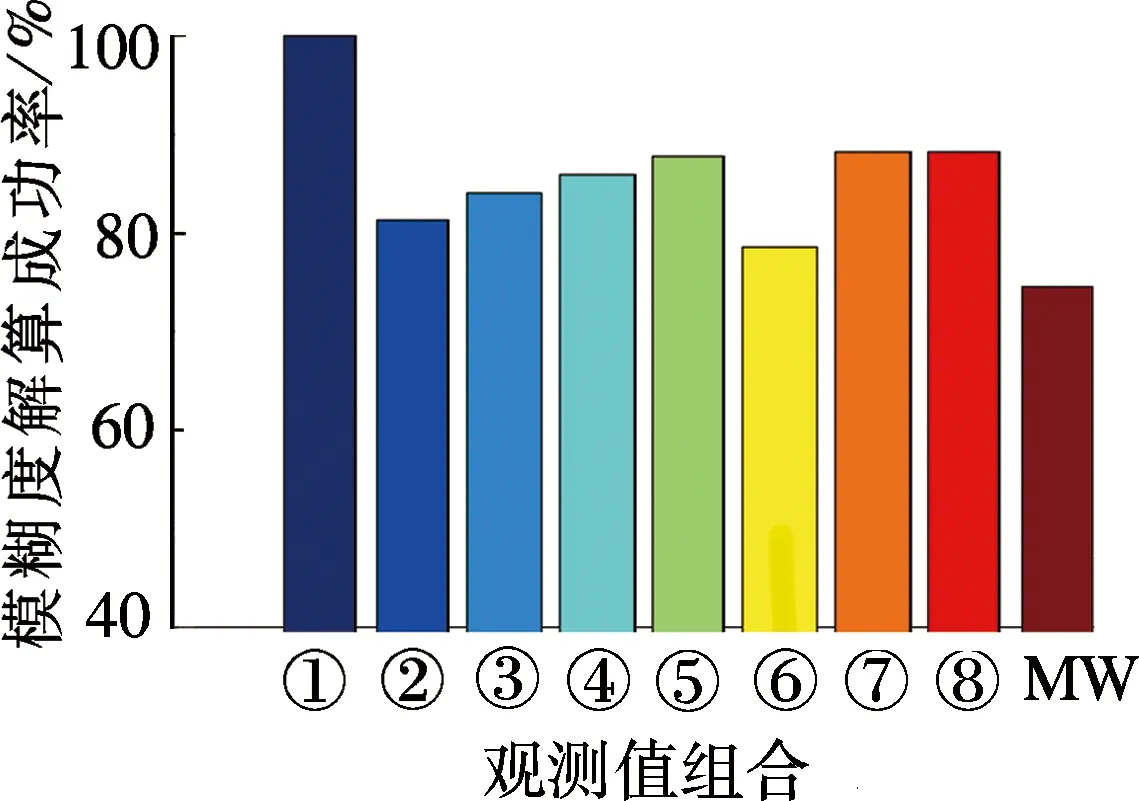
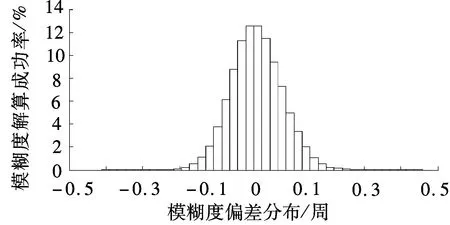
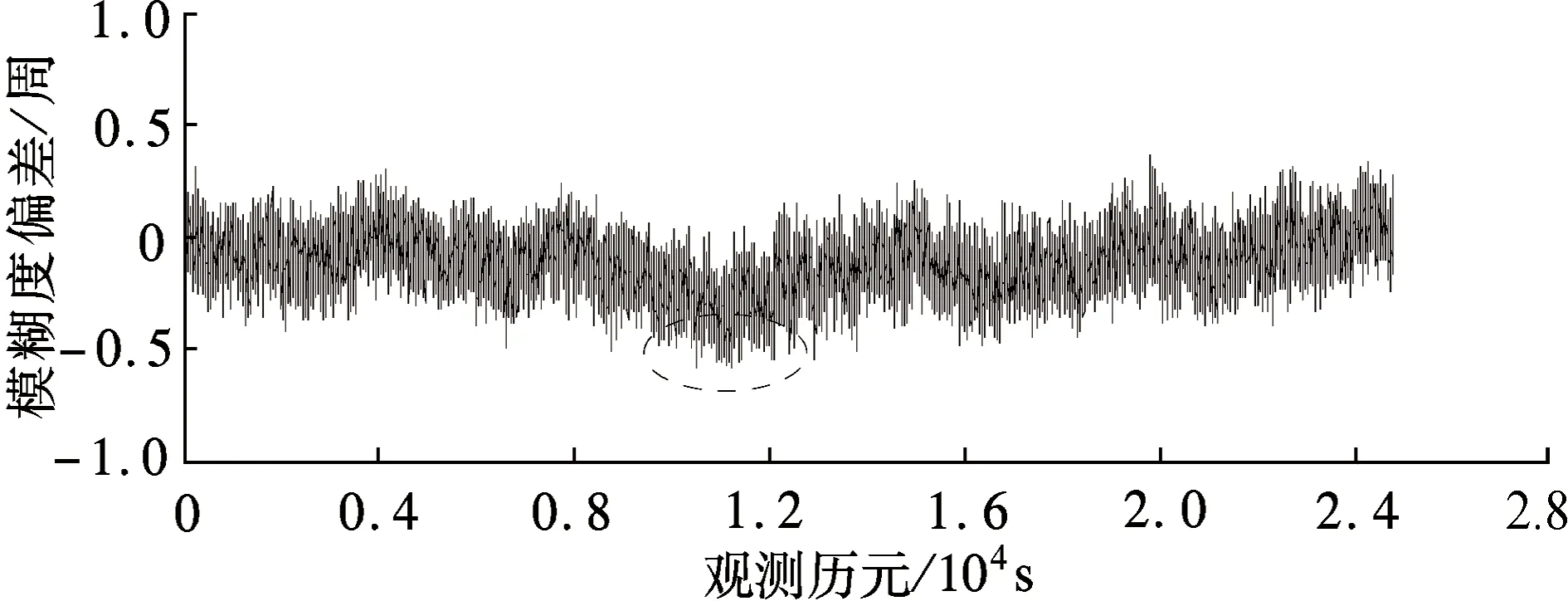
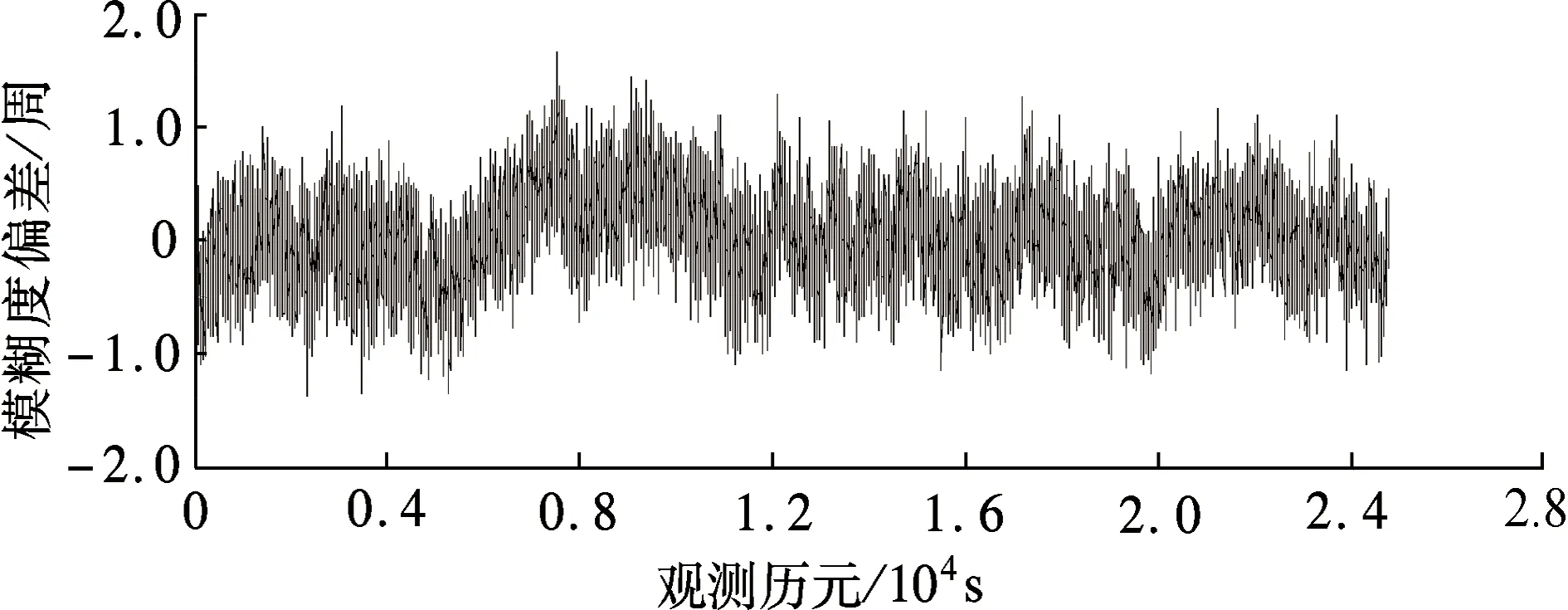
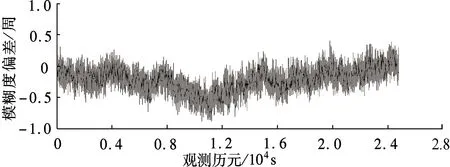
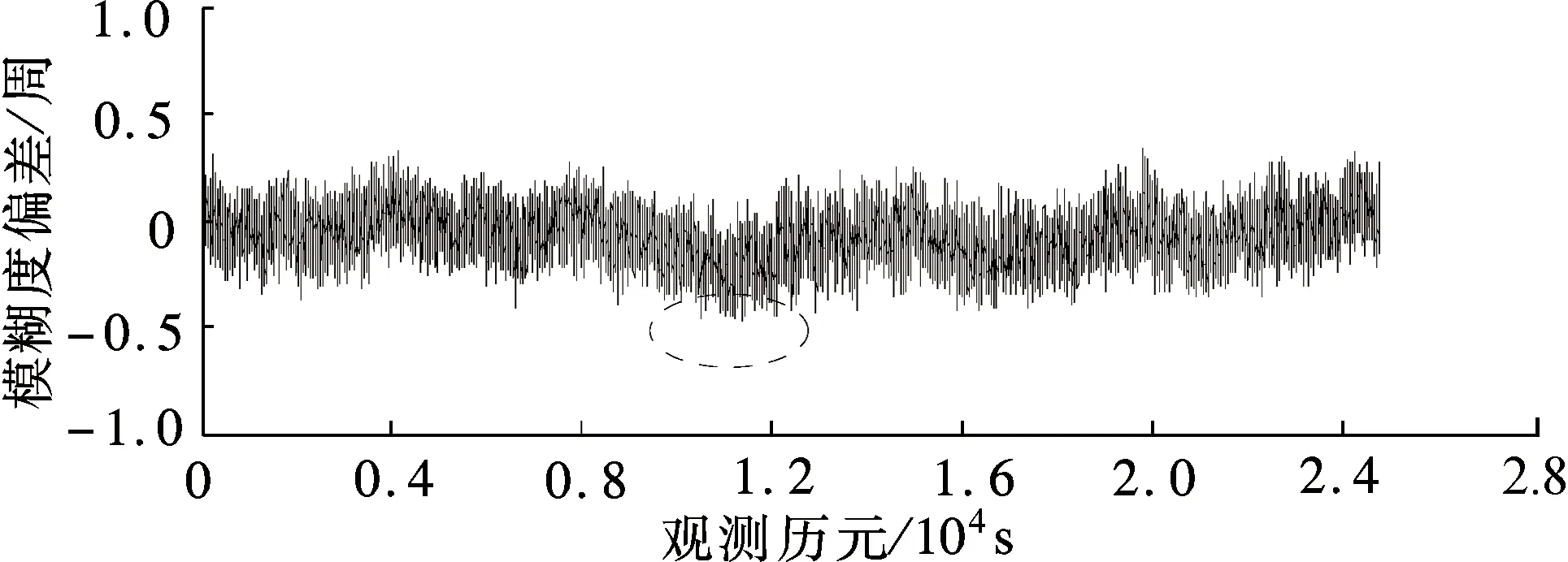
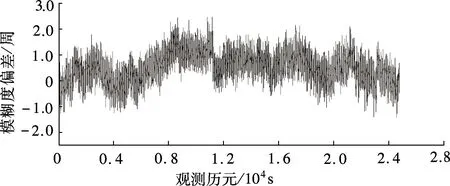
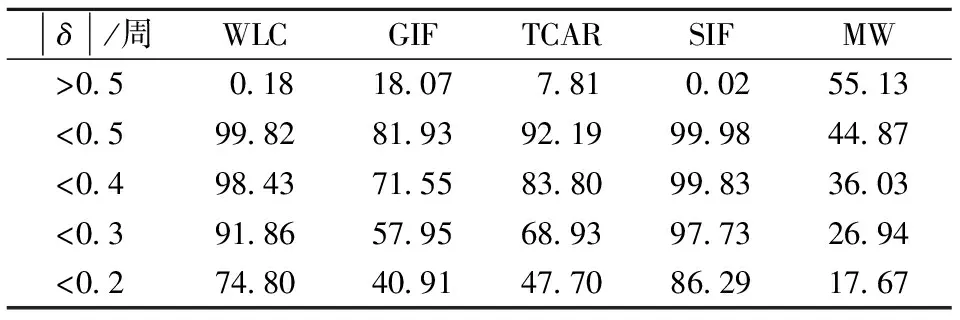
P(-0.5 (8) 式中,δ为由未模型化双差大气误差引起的系统性偏差;σ为由观测值噪声引起的模糊度解算中误差,分别为 (9) (10) 从图1中可以看出,采用WLC方法,随着未模型化双差大气误差的增大,模糊度解算成功率逐渐下降,其中(1,4,-5)组合受到的影响最小,在未模型化双差大气误差达到2 m时,模糊度解算成功率大于98%.对于电离层平静时的中长基线,使用WLC方法能够获得理想的模糊度解算成功率.但由于残留了双差电离层延迟,因此当基线长度增加且电离层活跃(如磁暴)时,采用WLC方法存在一定的不确定性. 2.1.2 三频载波伪距组合的无几何无电离层 与双频MW方法类似,根据式(1)和(2)的载波伪距观测方程组合,可得到求解模糊度的无几何无电离层方程,即 (11) 需满足以下2个条件: α+β+γ=1 (12) η(i,j,k)+η[α,β,γ]=0 (13) 式(12)保证了伪距和载波组合观测值中的几何项相同,能够消除对流层延迟、轨道误差等几何相关项的影响;式(13)保证了两者的电离层延迟大小相等,能够消除电离层延迟的影响.采用式(11)求解宽巷模糊度的精度为 (14) 从式(11)和(12)可以看出,无几何无电离层法求解宽巷模糊度仅受载波和伪距观测值噪声的影响,与基线距离无关.当给定载波组合系数时,通过使伪距观测值噪声最小即可获得最优组合,其等价于 α2+(q1β)2+(q2γ)2=min (15) 联立式(12)、(13)和(15),采用最小范数法求解最优的伪距组合系数[12].假设σΔφ=0.5 cm,伪距噪声为σΔP=0.3, 0.6 m两种情况,q1和q2分别取0.595和0.280[13],得到GIF法的伪距组合系数[α,β,λ],进而可根据式(8)获得模糊度解算成功率(此时系统性偏差δ=0),如图2所示.为了与双频情况下使用MW组合的结果进行对比,图2也同时给出了双频MW组合计算结果. (a) σΔφ=0.5 cm,σΔP1=0.3 m (b) σΔφ=0.5 cm,σΔP1=0.6 m 从图2中可以看出,使用GIF法求解宽巷模糊度,(0,-1,1)组合在不同伪距噪声情况下解算成功率接近100%,而其他组合受伪距噪声影响明显.解算(0,-1,1)组合模糊度时,利用组合的伪距ΔP(0,1,1)可获得与最优伪距组合相当的模糊度成功率[14],因此实际应用时大多直接采用ΔP(0,1,1)组合(ΔP(0,1,1)形式与式(3)相同),从而无需求解最优伪距组合系数,即 (16) 从图2中同时可以看出,三频GIF法解算成功率大多高于双频MW组合法,实际应用时只需解算出2个独立的宽巷模糊度即可通过整数组合得到任一系数和为0的宽巷模糊度,因此,三频GIF法解算效果明显优于双频MW组合法.GIF法仅受观测值噪声影响,当伪距精度较差时单历元成功率不高,需采取多历元平滑以提高解算成功率. 2.1.3 分步无几何方法 TCAR方法的主要思想是:首先利用无几何无电离层的载波伪距组合求解第1个超宽巷模糊度(0,-1,1)组合;然后利用模糊度固定的(0,-1,1)组合观测值与第2个宽巷观测值组成无几何模型以消除几何项的影响,其表达式为 (η(0,-1,1)-η(i,j,k)) ΔI+λ(0,-1,1)ΔN(0,-1,1)] (17) 由式(17)可知,TCAR方法求解宽巷模糊度主要受载波观测值噪声及残留的电离层延迟影响,即 (18) (19) 2.2 分步解算的无电离层法 由2.1节中GIF法分析可知,(0,-1,1)组合采用GIF法解算的成功率接近100%,且完全消除了几何项和一阶电离层延迟误差的影响,单历元能够可靠固定.当(0,-1,1)组合宽巷模糊度解算完成后,即可作为一个具有较高精度的观测量,用以辅助解算第2个宽巷模糊度.本文在WLC法和GIF法基础上提出一种分步解算的无电离层(SIF)方法,即采用(0,-1,1)组合观测值和另一个宽巷观测值组合成消电离层组合,其解算的表达式为 图3 TCAR方法模糊度解算成功率 (20) 式中,κ为(0,-1,1)组合的系数,为满足消去电离层的条件,需满足 η(i,j,k)+κη(0,-1,1)=0 (21) 使用式(21)求解宽巷模糊度的精度和残余几何项偏差的影响,可分别表示为 (22) (23) 图4 SIF方法模糊度解算成功率 采用一组实测的北斗三频基线数据进行实验,2个测站分别位于南京和上海,基线长度265 km,采集时间为2013年5月27日02∶18∶57—09∶12∶5,采样间隔1 s.图5给出了所有卫星利用GIF法求解(0,-1,1)组合模糊度的单历元偏差分布.从图中可以看出,(0,-1,1)组合模糊度的单历元解算偏差99.26%在±0.2周内,中误差为0.070 7周,因此单历元即可成功固定模糊度. 在(0,-1,1) 组合模糊度解算完成后,分别采用WLC法、GIF法、TCAR法以及本文提出的SIF法对第2个超宽巷或宽巷模糊度进行求解,由于在TCAR法和SIF法中所有组合性能相同,因此本文选择在WLC法、GIF法中总体性能较优的(1,4,-5)组合进行求解.本文仅给出一颗卫星的解算结果,如图6(a)~(d)所示.为体现三频相对双频在宽巷模糊度解算方面的优势,图7给出了双频情况下常用的MW组合解算结果.图6和图7中的模糊度准确值均通过长时间滤波解获得.在实际的模糊度解算中,为保证模糊度取整的正确性,通常会缩小取整的小数区间,因此表2对5种方法的模糊度偏差分布进行了统计. 图5 (0,-1,1) 组合超宽巷模糊度单历元解算偏差 对比图6和图7可以看出,三频情况下的4种方法结果均明显优于双频MW组合结果,图7中局部历元模糊度偏差甚至达到2.5周.影响MW组合精度的主要因素是伪距观测值质量,由此可以看出所采集数据的伪距观测值精度较差.分析图6中4种方法的计算结果可以看出:① GIF法虽然消除了对流层和电离层延迟的影响,但其受伪距观测质量的影响,单历元模糊度精度较差,需多个历元平滑处理;② 对比图6(a)、(c)、(d)可以看出,对于(1,4,-5) 组合模糊度,TCAR方法受电离层延迟影响最大,单历元解算结果呈现最明显的系统性偏差;而对于WLC方法,其长波长特性能够抵抗一定程度电离层延迟的影响,效果好于TCAR方法;而本文提出的SIF方法完全消除了电离层延迟的影响,其残余的对流层延迟误差远小于电离层延迟,解算效果最好.从图6(a)和(d)的标注区段可以看出,SIF方法优于WLC方法.从表2中也可看出,SIF法的单历元解算效果明显优于其他方法. (a) WLC (b) GIF (c) TCAR (d) SIF 图7 双频MW组合模糊度解算结果 % 对于中短基线,(1,4,-5)组合模糊度采用WLC方法能获得较高的解算成功率,但对于长基线且电离层活跃的情况,WLC方法解算成功率有一定不确定性.本文提出的SIF方法消除了电离层延迟的影响,仅残余了量级较小的几何项误差,且宽巷模糊度求解受观测值噪声影响仅为0.126 5周,单历元即可获得较高的模糊度解算成功率.GIF方法虽然消除了几何项误差和电离层延迟误差的影响,但由于引入了噪声较大的伪距观测组合误差,模糊度精度较低,特别是当伪距多路径误差显著时,模糊度解算成功率受到影响.TCAR方法由于残留了电离层延迟的影响,因此不适用于长基线情况,此外模糊度求解的精度也低于SIF方法.因此对于长距离参考站,SIF方法具有明显优势. References) [1]Landau H, Vollath U, Chen X. Virtual reference station systems[J].JournalofGlobalPositioningSystems, 2002, 1(2): 137-143. DOI:10.5081/jgps.1.2.137. [2]Hu G R, Khoo H S, Goh P C, et al. Development and assessment of GPS virtual reference stations for RTK positioning[J].JournalofGeodesy, 2003, 77(5): 292-302. DOI:10.1007/s00190-003-0327-4. [3]高旺, 高成发, 潘树国, 等. 北斗三频宽巷组合网络 RTK 单历元定位方法[J]. 测绘学报, 2015, 44(6): 641-648. DOI:10.11947/j.AGCS.2015.20140308. Gao Wang, Gao Chengfa, Pan Shuguo, et al. Single-epoch positioning method in network RTK with BDS triple-frequency widelane combinations [J].ActaGeodaeticaetCartographicaSinica, 2015, 44(6), 641-648. DOI:10.11947/j.AGCS.2015.20140308. (in Chinese) [4]Tang W, Meng X, Shi C, et al. Algorithms for sparse network-based RTK GPS positioning and performance assessment[J].JournalofNavigation, 2013, 66(3): 335-348. DOI:10.1017/s0373463313000015. [5]王伟亮, 高成发, 潘树国. 利用改进的相位平滑伪距公式求解网络 RTK 宽巷模糊度方法研究[J]. 测绘通报, 2012(4): 41-43. Wang Weiliang, Gao Chengfa, Pan Shuguo. Wide-lane ambiguity resolution of network RTK based on improved carrier phase smoothed pseudorange[J].BulletionofSurveyingandMapping, 2012(4): 41-43. (in Chinese) [6]Vollath U, Birnbach S, Landau L, et al. Analysis of three-carrier ambiguity resolution technique for precise relative positioning in GNSS-2[J].Navigation, 1999, 46(1): 13-23. DOI:10.1002/j.2161-4296.1999.tb02392.x. [7]Wang K, Rothacher M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data[J].JournalofGeodesy, 2013, 87(6): 539-553. DOI:10.1007/s00190-013-0630-7. [8]Feng Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J].JournalofGeodesy, 2008, 82(12): 847-862. DOI:10.1007/s00190-008-0209-x. [9]Li B, Feng Y, Shen Y. Three carrier ambiguity resolution: Distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J].GPSSolutions, 2010, 14(2): 177-184. DOI:10.1007/s10291-009-0131-6. [10]Tang W, Deng C, Shi C, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J].GPSSolutions, 2014, 18(3): 335-344. DOI:10.1007/s10291-013-0333-9. [11]Teunissen P J G. Influence of ambiguity precision on the success rate of GNSS integer ambiguity bootstrapping[J].JournalofGeodesy, 2007, 81(5): 351-358. DOI:10.1007/s00190-006-0111-3. [12]李金龙. GNSS 三频精密定位数据处理方法研究 [D]. 郑州:解放军信息工程大学测绘学院, 2011. [13]Gao W, Gao C, Pan S. Single-epoch navigation performance with real BDS triple-frequency pseudorange and EWL/WL observations[J].TheJournalofNavigation, 2016, 69(6): 1293-1309. DOI:10.1017/s0373463316000060. [14]Feng Y, Rizos C. Network-based geometry-free three carrier ambiguity resolution and phase bias calibration[J].GPSSolutions, 2009, 13(1): 43-56. DOI:10.1007/s10291-008-0098-8. [15]Feng Y M, Li B F. Wide area real time kinematic decimetre positioning with multiple carrier GNSS signals[J].ScienceChinaEarthSciences, 2010, 53(5): 731-740. DOI:10.1007/s11430-010-0032-0. Stepwise ionosphere-free wide-lane ambiguity method for long-range base stations with BDS triple-frequency observation Gao Wang1Gao Chengfa1Pan Shuguo2Qiao Longlei1Zhao Qing1 (1School of Transportation, Southeast University, Nanjing 210096, China) (2School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China) Aiming at the triple-frequency wide-lane/extra-wide-lane ambiguity resolution for long-range base stations of Beidou navigation satellite system (BDS), the main factors and limitations were analyzed for wide-lane combination (WLC) method, the carrier and pseudorange combined geometry-free and ionosphere-free (GIF) method, the three-carrier ambiguity resolution (TCAR) method. Then, a new stepwise ionosphere-free (SIF) method was proposed based on the characteristics known by baseline components. First, the (0,-1,1) ambiguity could be solved reliably with single epoch. After that, in order to solve the second wide-lane ambiguity, the ambiguity-fixed (0,-1,1) observation was used to form a ionosphere-free carrier observation together with the second wide-lane combination. The effects on the residual geometry errors were analyzed. BDS triple-frequency baseline data with a real distance of 265 km were used to test the performance. The results indicate that the proposed SIF method can avoid the influence of ionosphere delay on long-range baselines with smaller observation noises. Beidou navigation satellite system (BDS); triple frequency; wide lane ambiguity; long-range baseline; ionosphere delay 第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.009 2016-07-08. 作者简介: 高旺(1989—),男,博士生;高成发(联系人),男,博士,教授,博士生导师,gaochfa@seu.edu.cn. 国家自然科学基金资助项目(41574026)、中央高校基本科研业务费专项资金资助项目(KYLX15_0159)、东南大学优秀博士学位论文培育基金资助项目(YBJJ1635). 高旺,高成发,潘树国,等.基于分步无电离层组合的北斗三频长距离参考站间宽巷模糊度解算方法[J].东南大学学报(自然科学版),2017,47(1):43-49. 10.3969/j.issn.1001-0505.2017.01.009. P228.1 A 1001-0505(2017)01-0043-07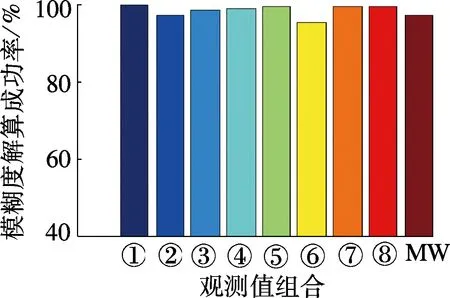
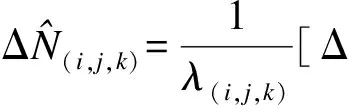
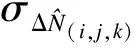
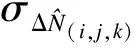
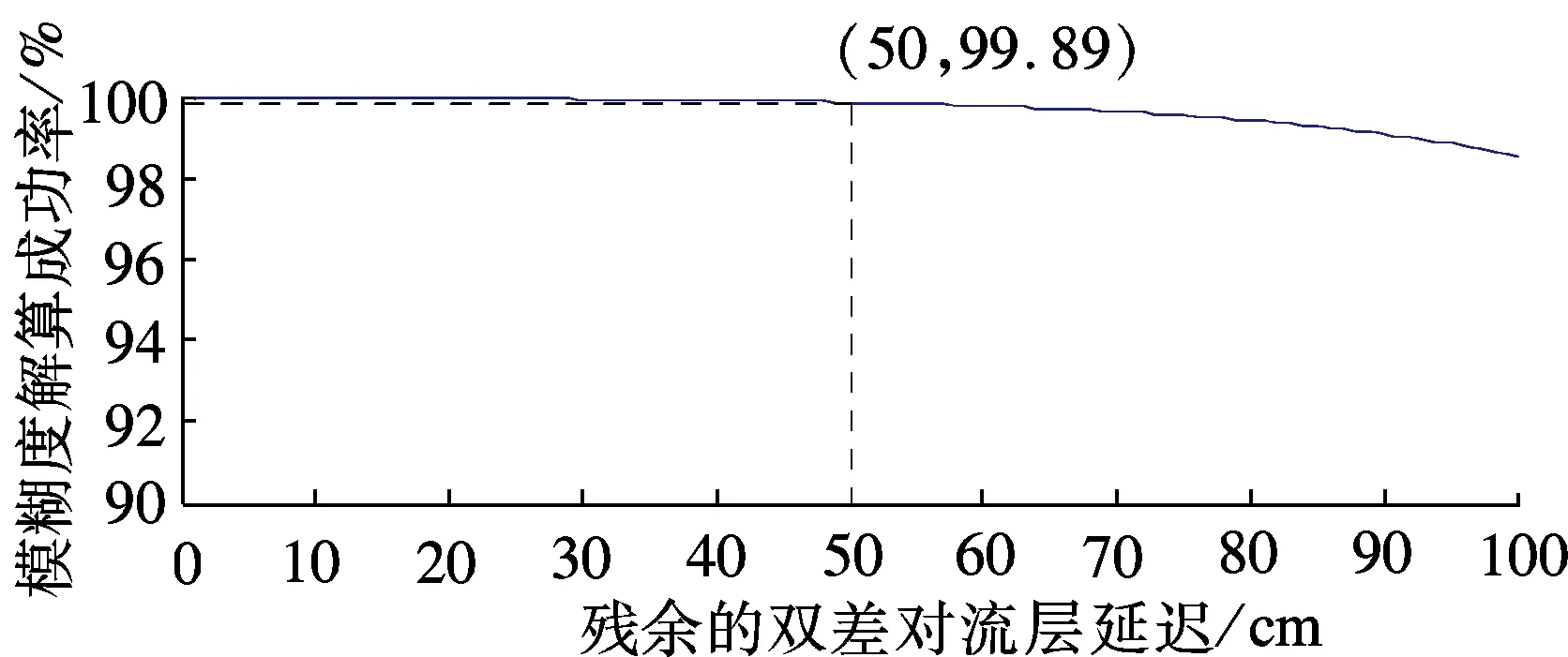
3 实验分析
4 结语