非对称量子乘积-张量积码

2017-02-09樊继豪陈汉武李荣贵

东南大学学报（自然科学版） 2017年1期

关键词：张量积乘积对偶

樊继豪陈汉武,2 李荣贵

(1东南大学计算机科学与工程学院, 南京 211189)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 211189)

非对称量子乘积-张量积码

樊继豪1陈汉武1,2李荣贵1

(1东南大学计算机科学与工程学院, 南京 211189)(2东南大学计算机网络和信息集成教育部重点实验室, 南京 211189)

针对绝大多数量子信道模型中发生量子比特翻转错误概率远小于发生量子相位翻转错误概率这一非对称的物理现象,基于经典乘积码与张量积码构造了非对称量子乘积-张量积码. 利用经典乘积码来纠正量子比特翻转错误,利用经典张量积码来纠正量子相位翻转错误.当2个组成子码皆满足对偶包含条件时,经典乘积码与张量积码满足对偶包含条件．基于3类满足对偶包含条件的经典纠错码,构造了具有新的参数非对称量子纠错码. 结果表明,该类非对称量子乘积-张量积码具有显著的非对称性．通过与已存在的非对称量子纠错码对比可以发现,所构造的部分非对称量子乘积-张量积码的参数优于其他已知的非对称量子纠错码.

量子纠错码;非对称量子纠错码;乘积码;张量积码

在量子计算与量子通信过程中, 量子系统和外部环境之间不可避免地会产生交互作用, 导致量子系统的相干性严重衰减, 产生量子消相干效应. 量子消相干效应所造成的量子噪声干扰是量子信息处理过程中所面临的一大主要障碍. 为了保护量子信息、对抗量子消相干效应以及其他量子噪声影响, 学者们通过借鉴经典纠错码的冗余纠错思想, 提出了量子纠错码理论[1].量子稳定子码构造理论[2]则提供了由经典加性码构造量子码的统一构造框架.

在绝大多数的量子力学系统中,量子错误发生概率具有显著的非对称性,发生量子比特翻转错误(X类型错误)的概率远小于发生量子相位翻转错误(Z类型错误)的概率. 为了在量子纠错过程中考虑这种非对称性,提出了非对称量子纠错码的概念[3].

经典乘积码[4]通过对2个经典线性码的生成矩阵进行张量积运算,将所得矩阵作为经典乘积码的生成矩阵.利用乘积码的构造方法来构造最小距离很大的线性码.利用基于软输入/软输出的Chase行/列迭代译码器,乘积码可以逼近香农界[5]. 张量积码则是利用2个线性码的校验矩阵进行张量积运算,将运算后所得矩阵作为张量积码的校验矩阵,具有纠正多个突发错误的能力[6]. Grassl等[7]基于张量积码构造了量子分组码与量子卷积码;La Guardia[8]基于经典Reed-Solomon码的乘积码构造了非对称量子乘积码.

本文基于乘积码与张量积码构造了非对称量子码. 经典乘积码具有大的最小距离,用于纠正Z类型错误;经典张量积码具有较高的维数,用于纠正X类型错误.

1 基本概念

1.1 非对称量子纠错码

记C为复数域,对于正整数n, 记Vn=(Cq)⊗n=Cqn为复数域Cq的n次张量积,对非对称量子码进行如下定义.

定义1 记码长为n的q元非对称量子码为Q=[[n,k,dz/dx]]q,那么Q为有限域Fq上希尔伯特空间Cqn的一个qk维子空间,它能够同时纠正(dx-1)/2个量子比特翻转错误和(dx-1)/2个量子相位翻转错误.

文献[3]给出了利用经典线性码来构造非对称量子码的结论.

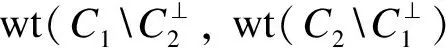
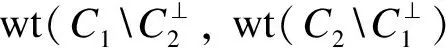
进一步,如果dz=wt(C2),dx=wt(C1),那么Q为纯码.

1.2 经典乘积码与张量积码

经典乘积码通过对2个经典线性码的生成矩阵做张量积运算,将所得矩阵作为乘积码的生成矩阵. 令D1与D2表示参数分别为[n1,k1,d1]q与[n2,k2,d2]q的线性码,并且D1,D2的生成矩阵分别为G1,G2,则D1与D2的乘积码为

P=D1⊗D2

P的生成矩阵GP为G1与G2的张量积矩阵,即GP=G1⊗G2

乘积码P的参数为[n1n2,k1k2,d1d2]q,其编码结构见图1.

图1 乘积码P=D1⊗D2的编码结构

令D1与D2的校验矩阵分别为H1与H2,则乘积码P=D1⊗D2的校验矩阵为

式中,A1为k1×n1的矩阵,并且与H1张成整个向量空间;A2为k2×n2的矩阵,并且与H2张成整个向量空间.

乘积码的解码过程如下:假定乘积码P根据图1所示的编码结构进行编码,并且按行传输.在接收端,收到的长度为n1n2的信息比特被重新按行排列为n1×n2的阵列结构,译码按照行/列译码的原则,即先进行行译码再进行列译码,并且可以迭代进行行/列译码,以增强译码效果.译码复杂度为分别进行行译码与列译码的复杂度之和,因此译码效率较高.

张量积码则是利用2个线性码的校验矩阵做张量积运算,将所得矩阵作为张量积码的校验矩阵.D1与D2的张量积码为

T=D1⊗hD2

张量积码T的校验矩阵为H1与H2的张量积,即

HT=H1⊗H2

T的参数为[n1n2,n1n2-ρ1ρ2,min {d1,d2}]q,其中,ρ1=n1-k1与ρ2=n2-k2分别为D1与D2的校验位数.

2 非对称量子乘积码-张量积码的构造

由定理1可知,非对称量子码构造的关键在于寻找2个满足对偶包含条件的经典码. 由乘积码与张量积码的校验矩阵形式可知,如果其组成子码皆满足对偶包含条件,那么乘积码与张量积码亦满足对偶包含条件.

因此,乘积码P与张量积码T是对偶包含的. 证毕.

如果D1与D2分别具有纠正l1与l2个突发错误的能力,那么由文献[4]可知,乘积码P=D1⊗D2具有纠正max(n1l2,n2l1)个突发错误的能力;由文献[6]可知,张量积码具有纠正l1个突发错误子块的能力. 证毕.

2.1 非对称量子乘积-张量积Hamming码

文献[9]基于经典Hamming码构造了一类乘积码,该类乘积码在进行基于迭代的Turbo译码时可以逼近香农界.下面利用满足对偶包含条件的Hamming码来构造非对称量子乘积-张量积Hamming码.

表1列出了二元域(q=2)下m1与m2取值不同时所构造出的部分二元非对称量子乘积-张量积Hamming码.

表1 非对称量子乘积-张量积Hamming码

2.2 非对称量子乘积-张量积BCH码

文献[5]基于BCH码构造了乘积码,该类乘积码在进行基于软输入/软输出的Chase行/列迭代译码时可以逼近香农界. 下面利用对偶包含BCH码构造非对称量子乘积-张量积码．为了简单起见,此处仅考虑基于狭义本原BCH码的非对称量子乘积-张量积BCH码的构造.

令F1与F2分别表示设计距离为δ1与δ2的狭义本原BCH码,其参数分别为[n1,k1,δ1]q与[n2,k2,δ2]q,其中n1=qm1-1,n2=qm2-1,k1=n1-m1(δ1-1)(1-1/q),k2=n2-m2(δ2-1)(1-1/q),设计距离满足如下条件:

δ1≤qm1/2-1-(q-2)m1为奇数

δ2≤qm2/2-1-(q-2)m2为奇数

冗余位数分别为

ρ1=m1(δ1-1)(1-1/q)

ρ2=m2(δ2-1)(1-1/q)

表2列出了F1=F2时基于对偶包含BCH码所构造出的部分非对称量子乘积-张量积BCH码.

表2 非对称量子乘积-张量积BCH码

2.3 非对称量子乘积-张量积MDS码

文献[11-12]基于各类经典MDS码构造了大量新的码长稀疏的量子MDS码. 下面基于对偶包含MDS码来构造非对称量子乘积-张量积MDS码.

由定理2可知,构造非对称量子乘积-张量积MDS码的关键是寻找2个满足对偶包含条件的经典MDS码. 令L1与L2分别表示参数为[n1,k1,d1]q与[n2,k2,d2]q并且满足对偶包含条件的q元经典MDS码,其中k1=n1-d1+1,k2=n2-d2+1,3≤n1,n2≤q+1,2≤d1≤n1/2+1,2≤d2≤n2/2+1. 因此,存在参数为[[n1n2,k1k2-(d1-1)(d2-1),d1d2/min{d1,d2}]]q的非对称量子乘积-张量积MDS码.

表3列出了L1=L2时基于对偶包含MDS码所构造出的部分非对称量子乘积-张量积MDS码.

2.4 结果分析与对比

文献[2]基于量子Hamming码[[7,1,3]]构造出级联量子码[[49,1,9]];文献[13]将该类码应用于容错量子计算中,以保护量子逻辑门免受噪声干扰．与[[49,1,9]]级联量子码相比,本文表1中构造的非对称量子乘积-张量积码[[49,7,9/3]]具有更高的码率,同时具有和[[49,1,9]]相同的纠正Z类型错误的能力．

表3 非对称量子乘积-张量积MDS码

表3中的非对称量子乘积-张量积码[[49,21,9/3]]8与[[100,60,9/3]]11分别优于文献[8]中的非对称量子码[[49,16,9/3]]8与[[100,55,9/3]]11．表3中的非对称量子乘积-张量积码的[[100,60,9/3]]9,[[100,60,9/3]]11与[[121,77,9/3]]11分别优于文献[14]中的[[100,50,9/3]]9,[[100,50,9/3]]11与[[121,11,9/3]]11．

3 结语

结合经典乘积码与张量积码提出了非对称量子乘积-张量积码的构造方法,并且根据3类满足对偶包含条件的经典纠错码构造了具有新的参数非对称量子纠错码. 非对称量子乘积-张量积码充分考虑了乘积码与张量积码在最小距离方面的非对称性,并利用各自的优势来分别纠正Z类型错误与X类型错误,能够适应量子信道的非对称性. 所构造的部分非对称量子乘积-张量积码的参数优于其他已知的非对称量子码.如何基于软输入/软输出进行非对称量子乘积-张量积码的迭代译码需要进一步研究.

References)

[1]Shor P W. Scheme for reducing decoherence in quantum computer memory[J].PhysicalReviewA, 1995, 52(4): R2493-R2496. DOI:10.1103/physreva.52.r2493.

[2]Gottesman D. Stabilizer codes and quantum error correction[D]. Pasadena, CA, USA: California Institute of Technology, 1997.

[3]樊继豪,陈汉武,阮越,等. 基于经典Goppa码的非对称量子稳定子码构造[J].中国科学: 信息科学, 2013, 43(3): 407-417. Fan Jihao, Chen Hanwu, Ruan Yue, et al. Constructions of asymmetric quantum stabilizer codes based on classical Goppa codes[J].ScientiaSinicaInformationis, 2013, 43(3): 407-417. (in Chinese)

[4]MacWilliams F J, Sloane N J A.Thetheoryoferror-correctingcodes[M]. Amsterdam, the Netherlands: North-Holland,1981: 568-571.

[5]肖海林, 欧阳缮, 谢武. 量子 Turbo 乘积码[J]. 物理学报, 2011, 60(2): 15-21. Xiao HaiLin,Ouyang Shan,Xie Wu. Quantum Turbo product codes[J].ActaPhysicaSinica, 2011, 60(2): 15-21.(in Chinese)

[6]Wolf J K. On codes derivable from the tensor product of check matrices[J].IEEETransactionsonInformationTheory, 1965, 11(2): 281-284. DOI:10.1109/tit.1965.1053771.

[7]Grassl M, Rötteler M. Quantum block and convolutional codes from self-orthogonal product codes[C]//ProceedingsoftheIEEEInternationalSymposiumonInformationTheory. Adelaide, Australia, 2005: 1018-1022.

[8]La Guardia G G. Asymmetric quantum product codes[J].InternationalJournalofQuantumInformation, 2012, 10(1): 1250005. DOI:10.1142/s0219749912500050.

[9]Nickl H, Hagenauer J, Burkert F. Approaching Shannon’s capacity limit by 0.27 dB using simple Hamming codes[J].IEEECommunicationsLetters, 1997, 1(5): 130-132. DOI:10.1109/4234.625034.

[10]Aly S A, Klappenecker A, Sarvepalli P K. On quantum and classical BCH codes[J].IEEETransactionsonInformationTheory, 2007, 53(3): 1183-1188.DOI:10.1109/TIT.2006.890730.

[11]Chen Bocong, Ling San, Zhang Guanghui. Application of constacyclic codes to quantum MDS codes[J].IEEETransactionsonInformationTheory, 2015, 61(3): 1474-1484. DOI:10.1007/s10773-014-2204-8.

[12]Kai X, Zhu S, Li P. Constacyclic codes and some new quantum MDS codes[J].IEEETransactionsonInformationTheory, 2014, 60(4): 2080-2086. DOI:10.1109/tit.2014.2308180.

[13]Nielsen M A, Chuang I L. 量子计算与量子信息 [M]. 北京: 清华大学出版社,2015: 425-493.

[14]La Guardia G G. Asymmetric quantum Reed-Solomon and generalized Reed-Solomon codes[J].QuantumInformationProcessing, 2012, 11(2): 591-604. DOI:10.1007/s11128-011-0269-3.

Asymmetric quantum product and tensor product codes

Fan Jihao1Chen Hanwu1,2Li Ronggui1

(1School of Computer Science and Engineering, Southeast University, Nanjing 211189, China) (2Key Laboratory of Computer Network and Information Integration of Ministry of Education, Southeast University, Nanjing 211189, China)

To solve the physical phenomenon that the probability of the quantum qubit-flipping errors is much less than that of the phase-flipping errors in many quantum channel models, the asymmetric quantum error-correcting codes (AQECCs), called as asymmetric quantum product and tensor product codes, are constructed based on classical product codes and tensor product codes. The product codes are used to correct the qubit-flipping errors and the tensor product codes are used to correct the phase-flipping errors. If the two component codes satisfy the dual containing conditions, then the resultant product codes and tensor product codes satisfy the dual containing conditions. A new class of AQECCs is constructed based on three classes of classical error-correcting codes satisfying the dual containing restrictions. The results show that that the proposed asymmetric quantum product and tensor product codes have obvious asymmetries. Compared with the known AQECCs, parts of the asymmetric quantum product and tensor product codes have better parameters than the known AQECCs.

quantum error-correcting code; asymmetric quantum error-correcting code; product code; tensor product code