GLONASS载波相位整周模糊度分析

田宇，翟建勇，袁润平，苏翠萍

（中国电子科技集团公司第二十研究所，西安 710068）

0 引言

GLONASS同GPS的设计原理及定位方式很相似，但由于GLONASS采用频分多址技术，即每颗卫星都使用不同的工作频率发射信号，这就使得现有的GPS数据处理方法无法对GLONASS观测数据进行处理。对载波相位观测数据而言，由于GLONASS卫星工作频率各不相同，因而无法按照GPS的数据处理模型处理 GLONASS观测数据。GLONASS整周模糊度参数和钟差参数是相关的，即无法把整周模糊度数与钟差参数分离出来。所以，无法采用标准的双差处理方法确定整周模糊度数，从而确定其它未知参数。文中主要讨论GLONASS组合载波相位测量中模糊度解算方法。

1 载波相位双差原理

载波相位差分定位模型由两台接收机构成，其中一台作为基准站，另一台作为移动站，基准站将原始观测数据实时传送到移动站，并可构建载波相位双差观测方程。通过载波相位双差可削弱甚至消除轨道误差、钟差、大气误差等误差影响，进行实时数据处理，从而实时确定流动站位置和速度。

如图1所示，假定在一个差分系统中，两个相距不远的用户接收机u和基准站接收机t同时跟踪编号分别为i和j的两颗卫星，并且相应的生成同一时刻的载波相位测量值。下面就把 GPS和GLONASS系统的测量值组合成单差载波相位以及双差载波相位测量值。此处单差指站间（即接收机之间）对同一颗卫星测量值的一次差分，而双差是指对两颗不同卫星的单差之间进行差分，即在站间和星间各求一次差分。由于GPS信号采取的是码分多址（CDMA）的方式，而GLONASS信号采取的是时分多址（FDMA）的方式，所以载波相位的单差以及双差结果也就不同，下面就对两个系统分别加以介绍。

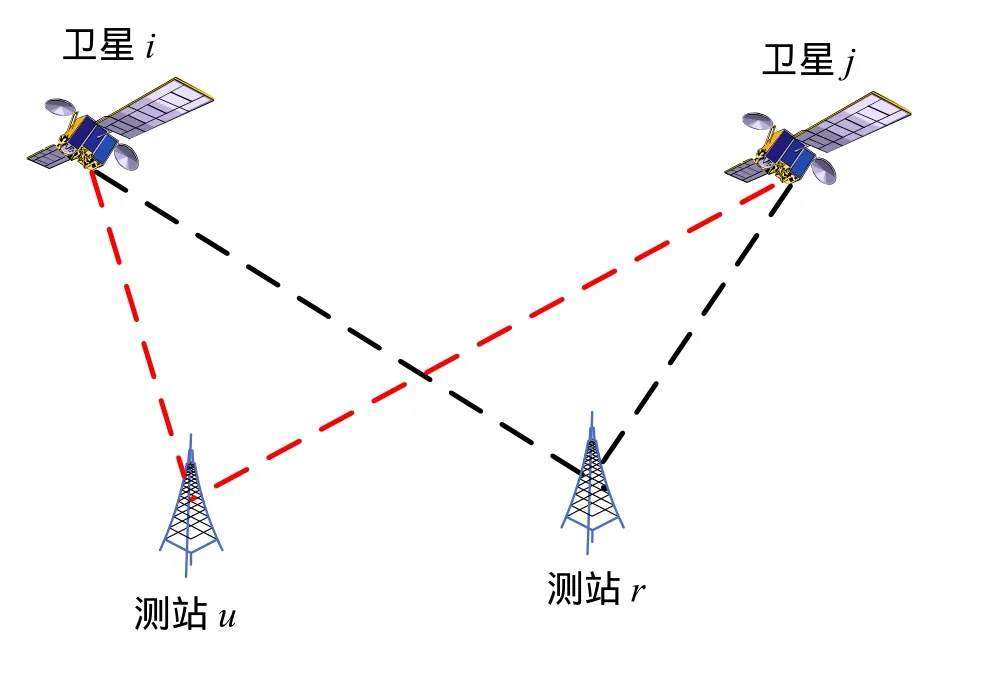
图1 双差相对定位示意图

1.1 GPS单差及双差载波相位

首先给出GPS载波相位观测方程式如式（1）：

其中：φ(sGPS)：载波相位观测量；λGPS：GPS信号载波波长；fGPS：GPS信号载波频率；r(sGPS)：接收机到卫星的距离；I(sGPS)：电离层延时参数；T(sGPS)：对流层延时参数；Lu,GPS：接收机在各个GPS信道上的群波延时；δtu,GPS：接收机钟差；δt(sGPS)：卫星钟差；N(sGPS)：载波相位整周模糊度；：载波相位测量噪声。

参照式（1），用户接收机u和r在同一时刻对同一颗GPS卫星iGPS的载波相位测量值的观测方程式分别表达如下：

两接收机u和r对卫星iGPS的单差载波相位测量值则为：

其中δturL,GPS=(δtu,GPS+Lu,GPS)-(δtr,GPS+Lr,GPS)为包括单差接收机器件群波延时在内的单差接收机钟差。

从式（4）可以看出，单差载波相位卫星钟差δt(iGPS)被彻底消除，对于短基线及零基线系统而言，单差电离层延时和单差对流层延时均约等于零，于是单差载波相位观测方程可以简化为：

根据式（5）可以推导出，两接收机u和r对两卫星iGPS和jGPS的双差载波相位测量值φ(ijGPS)ur如下：

从式（6）可以看出，双差载波相位能彻底消除GPS卫星钟差、接收机钟差、电离层延时和单差对流层延时，对于零基线系统而言，不考虑载波相位测量噪声的情况下，双差载波相位结果应该具有整数周的特性。GPS载波相位双差结果如图2所示。

图2 GPS载波相位双差结果

1.2 GLONASS单差及双差载波相位

对GLONASS载波相位测量值的单差处理在原理上与对GPS载波相位测量值的单差处理相同，但由于GLONASS每颗星的发射频率各不相同，载波相位测量值中的接收机通道间的延时不能被忽略，因此对GLONASS载波相位测量值的单差及双差处理会更复杂一些。首先给出GLONASS载波相位观测方程式如式（7）。

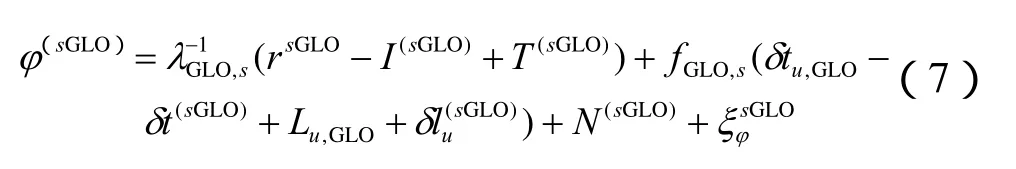
其中，φ（sGLO）：GLONASS载波相位观测量；λGLO,s：GLONASS信号载波波长；fGLO,s：GLONASS信号载波频率；r(sGLO)：接收机到卫星的距离；I(sGLO)：电离层延时参数；T(sGLO)：对流层延时参数；Lu,GLO：接收机在各个 GLONASS信道上的群波延时平均值；：处理卫星s的接收机信道群波延时的非公共部分，不同卫星有不同的值；δtu,GLO：接收机钟差；δt(sGLO)：卫星钟差；N(sGLO)：载波相位整周模糊度；：载波相位测量噪声。

参照式（7），用户接收机u和r在同一时刻对同一颗 GLONASS卫星iGPS的载波相位测量值的观测方程式分别表达如下：

两接收机u和r对卫星iGPS的单差载波相位测量值则为：

其中δturL,GLO=(δtu,GLO+Lu,GLO)-(δtr,GLO+Lr,GLO)为包括单差接收机器件群波延时在内的单差接收机钟差。

从式（10）可以看出，对于短基线及零基线系统而言，单差电离层延时和单差对流层延时均约等于零，于是单差载波相位观测方程可以简化为：

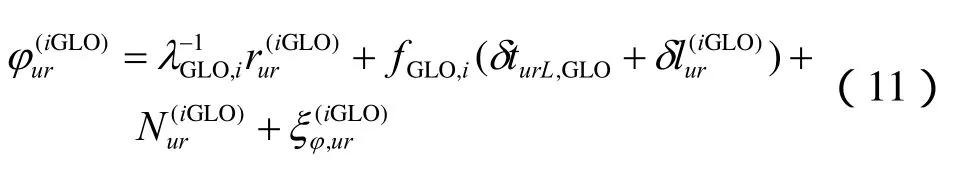
根据式（11），GLONASS单差载波相位卫星钟差δt(iGLO)被彻底消除，单差接收机通道间延时差异和单差整周模糊度为两个未知参量，特别是对于不同的卫星有着不同的值。假设两接收机u和r来自同一个生产商，则可以认为等于零。

根据式（11）可以推导出，两接收机u和r对两卫星iGLO和jGLO的双差载波相位测量值如下：

从式（12）可以看出，与GPS双差载波相位测量值不同，因为不同GLONASS卫星信号的载波频率各不相同，所以对GLONASS载波相位测量值的双差处理并不能消除接收机钟差δturL,GLO，因此，对GLONASS系统而言，不考虑载波相位测量噪声的情况下，双差载波相位结果应该不具有整数周的特性。GLONASS载波相位双差结果如图3所示。

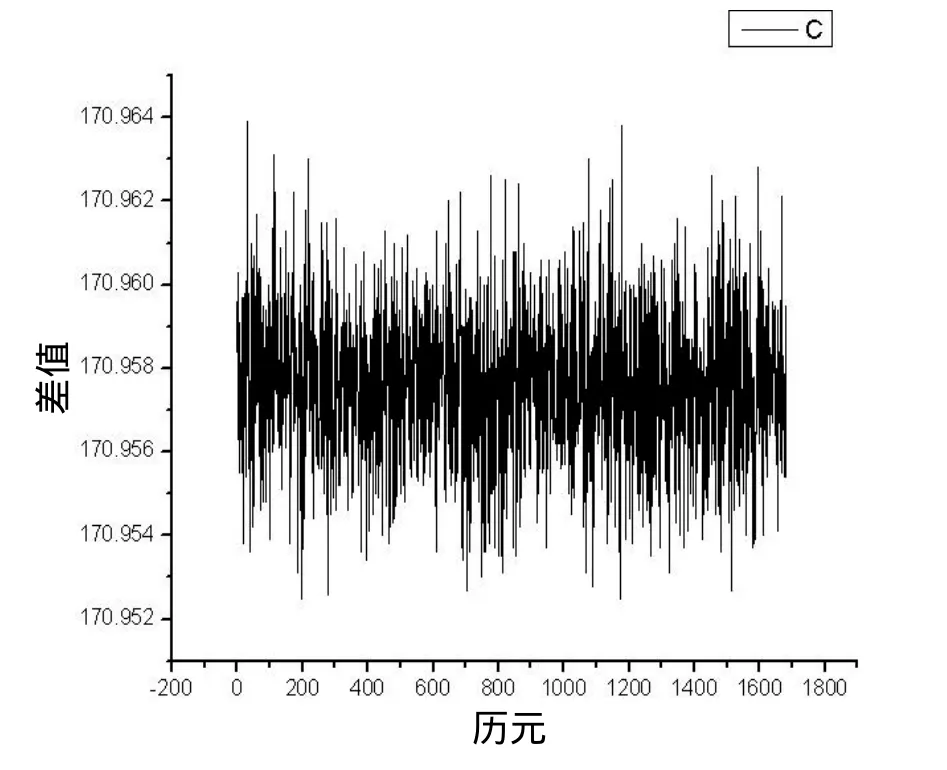
图3 GLONASS载波相位双差结果

将式（11）乘以波长，得出：

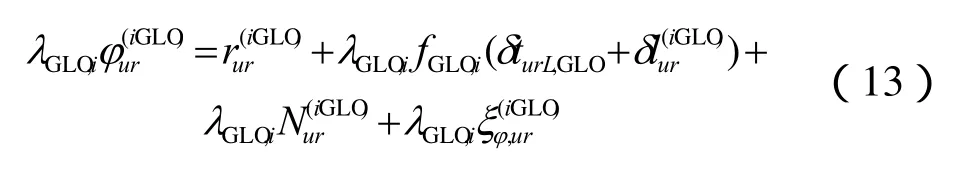
对式（13）进行双差，结果如下：

这样，消除了接收机钟差的影响。在式(14)中，GLONASS双差模糊度与GPS模糊度明显不同的是它不但复杂，而且还不再具 有整周特性，对式（14）中的双差模糊度进行如下变换：

2 GLONASS载波整周模糊度处理

经过变换，将原来的由两个单差模糊度项组成的不具有整周特性的双差模糊度，变成一个具有整周特性的双差模糊度和一个与参考卫星的单差模糊度有关的两部分。上述变换使双差模糊度具有整周特性，可以进一步固定双差模糊度。变换后产生的与单差模糊度及两颗卫星的波长差有关。当卫星间波长差很小或单差模糊度的精度达到几周时，小于0.1周，可以得出整周模糊度。参考卫星的单差模糊度可由码伪距得出近似值，用码伪距得到的的极差小于10周；用 P码伪距所求出的的极差小于5周。对精度要求不高时，可以用伪距法得出单差模糊度的近似值，然后就可以按GPS常规方法求解。当精度要求较高时，用迭代法求出双差模糊度的整数值及单差模糊度的值，然后再求解固定解。

3 结语

GPS载波相位测量技术目前已经成熟。在测量领域等方面得到广泛的应用。GLONASS发射两种载波，但是由于采用频分多址的方式区分卫星信号，每个卫星发射的载波频率各不相同。这就造成了GLONASS载波相位测量与GPS载波相位测量之间有很大的区别。虽然与GPS相同，GLONASS单差观测量中也消去了卫星钟钟差的影响，但是在GLONASS载波相位双差观测量中无法消去接收机钟差参数。所以在GLONASS载波相位测量中必须采用与 GPS双差处理不同的方法确定整周模糊度数，进而确定其它未知参数。

[1]Leick A.A Spects of GLONASS Carrier-phase Differencing [J].GPS,1998.

[2]Leick A.GLONASS Satellite Surveying Engineering [J].1998,124(2).

[3]Takasu T.Yasuda A.Development of the low Cost RTK-GPS Receiver with an open Source Program package RTKLIB[C].International Symposium on GPS/GNSS,Korea,2009,4-6.