风力机传动链齿轮齿根疲劳裂纹扩展剩余寿命评估

肖俊峰，李建兰

(华中科技大学 能源与动力工程学院，武汉 430074)

风力机传动链齿轮齿根疲劳裂纹扩展剩余寿命评估

肖俊峰，李建兰

(华中科技大学 能源与动力工程学院，武汉 430074)

在叶轮气动载荷模型、柔性传动链模型和齿根弯曲应力模型的基础上，建立了随机风速下风力机传动链齿轮齿根疲劳裂纹扩展剩余寿命计算模型，对不同风速下的齿根弯曲应力进行了计算，分析了随机载荷下裂纹的扩展速率.对1.5 MW风力机太阳轮齿根疲劳裂纹的扩展进行了分析.结果表明：风力机齿轮齿根疲劳裂纹扩展寿命主要受风载荷影响，且紧急制动等冲击对裂纹扩展后期的影响不可忽视.

风力机；齿轮；裂纹扩展；紧急制动；剩余寿命评估

随着化石能源枯竭和环境危机加剧，风能、太阳能等可再生能源日益得到重视.根据全球风能协会发布的报告：2014年底我国风电装机容量突破114 GW，但风电等效运行小时不超过2 000 h，制约了我国风电的发展.导致风力机利用率不高的原因包括弃风限电及风力机本身故障等原因.齿轮箱故障通常会导致机组长时间停机，轮齿断裂是齿轮常见故障之一，主要由轮齿裂纹扩展导致[1-5].为了保障风电机组的安全运行，有必要对齿轮齿根疲劳裂纹扩展剩余寿命进行研究.

可靠的齿轮载荷谱需通过电测法长时间不间断测量后统计得到[6].但电测法成本高，实现难度大，实际上一般通过齿轮箱的输入载荷估算齿轮的载荷.沈亮等[7-8]利用雨流计数法对实测数据计数得到齿轮箱输入轴载荷谱，并计算得到齿根弯曲应力分布.秦大同等[9-11]通过建立风力机传动链动力学模型，得到了随机风速下齿轮箱动态外载荷.Heege等[12]利用有限元法建立了风力机的多体动力学模型，得到紧急制动工况下齿轮箱的载荷.Sun等[13]通过建立齿轮载荷分布与风速分布的关系，获得了正态分布风速下的齿轮载荷分布.祖世华[14]提出一种编制载荷谱的新方法，计算得到齿轮弯曲疲劳载荷谱.

在风电齿轮齿根疲劳裂纹扩展剩余寿命研究方面，周璇等[15]利用Abaqus软件对风电齿轮箱太阳轮进行了有限元建模，计算了含齿根疲劳裂纹的太阳轮的齿根应力强度因子和裂纹前缘应力强度因子，分析了外加载荷对应力强度因子的影响.田雪[8]根据断裂力学对风力机齿轮齿根疲劳裂纹扩展进行了建模，估算了等效载荷下齿根疲劳裂纹扩展寿命.

风力机的载荷较为复杂，会受到由紧急制动导致的远大于正常运行载荷的冲击载荷的影响，但目前对风力机齿轮箱齿轮齿根疲劳裂纹扩展剩余寿命的评估中还未考虑载荷随机性和冲击载荷的影响，也尚无通过风速的分布评估风力机齿轮箱齿轮齿根疲劳裂纹扩展剩余寿命的完整机理模型.因此，笔者在叶轮气动载荷计算模型、风力机传动链的动力学模型和齿根弯曲应力模型的基础上，建立了完整的风力机传动链齿轮齿根疲劳裂纹扩展剩余寿命机理模型，并以1.5 MW风力机齿轮箱行星级太阳轮为研究对象，研究了在实际风场中随机风载荷作用下的齿轮齿根疲劳裂纹扩展剩余寿命，以及紧急制动时极限载荷对疲劳裂纹扩展剩余寿命的影响.

1 风力机齿轮齿根弯曲疲劳载荷模型

1.1 输入风速的建模

根据文献[7],在风力机整个寿命周期，风力机正常发电工况占比为86.326 4%，停机工况占比为12.307 8%，其他工况占比为1.365 8%.可以看出，正常发电工况下的周期性载荷占比最大，机组起动、关机和紧急制动等工况引起的瞬时载荷在风力机寿命周期中的占比较小.因此，在风力机齿根弯曲疲劳载荷计算中主要考虑正常发电工况下的载荷，其他工况下只考虑瞬时载荷的极大值对疲劳裂纹扩展的影响.根据风力机的功率曲线，将风速分布划分为：

(1)当风速小于切入风速或大于切出风速时，风力机不发电，因此在计算载荷时不考虑此风速区间.

(2)当风速大于切入风速、小于额定风速时，风力机的转速和功率均随风速的变化而变化.因此，将风速以1 m/s为间隔划分为不同风速区间.

(3)当风速大于额定风速、小于切出风速时，风力机的功率和转速分别保持在额定功率和额定转速，将此风速段作为一个风速区间.

令风力机在不同风速v下的年运行小时向量为T={t1,t2,…,tn}，其中：

(1)

式中：ti为风力机在第i个风速区间的理论运行时间，s；f(v)为风速分布的概率密度函数；vmax,i为第i个风速区间的最大风速，m/s；vmin,i为第i个风速区间的最小风速，m/s.

根据风速的分布和风力机的功率曲线，风力机的理论年等效利用小时数T0为：

(2)

式中：Pi为第i个风速区间的平均风速下风力机的功率，kW；P0为风力机的额定功率，kW.

由于电网限电、风力机故障和风力机检修等原因，风力机的实际出力受到影响，导致其实际年等效利用小时数小于理论年等效利用小时数.因此，风场发电量综合折减系数ξ为[16]：

(3)

式中：T′为风力机的实际年等效利用小时数，h.

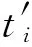
(4)

根据风力机的转速曲线及第i个风速区间下风力机的实际运行时间，第i个风速区间风力机齿轮箱输入端的旋转圈数Nin,i为：

(5)

式中：ωin,i为第i个风速区间的平均风速下风力机齿轮箱输入端的旋转角速度，rad/s.

根据第i个风速区间下齿轮箱输入端转速和齿轮箱传动比，可求得第i个风速区间下太阳轮轮齿的啮合次数，即齿根弯曲应力循环次数Ns,i为：

Ns,i=Nin,inp(N0s-1)

(6)

式中：np为与太阳轮啮合的行星齿轮的个数；N0s为太阳轮与齿轮箱输入端的传动比.

1.2 叶轮气动扭矩模型

叶轮的气动扭矩是风力机传动链的主要外部激励，笔者通过动量理论及叶素理论计算风速v下的气动扭矩.

假设在理想情况下[17]叶轮简化为一个叶片数为无穷的桨盘；气流不可压缩，是均匀定常流；叶轮旋转时无摩擦力；叶轮前后气流静压相等；叶轮流动模型简化为一个单元流管；叶轮圆环上的推力均匀分布.

根据动量理论，理想情况下作用在叶轮平面宽度为dr的微元圆环上的推力dFWT和扭矩dTWT为：

(7)

式中：ρ为气流密度，kg/m3；ωWT为叶轮转动角速度，rad/s；aaif为轴向速度诱导因子；baif为切向速度诱导因子；r为圆环的半径，m.

根据叶素理论，理想情况下作用在叶轮平面宽度为dr的微元圆环上的推力dFWT和扭矩dTWT为：

(8)

其中，

(9)

(10)

(11)

式中：Cn为法向力系数；Ct为切向力系数；vr为叶素圆环上相对风速，m/s；φ为入流角，rad；Cl为升力系数；Cd为阻力系数；cc为叶素弦长，m；BWT为叶片数.

由式(7)和式(8)可得：

(12)

其中，

(13)

实际风力机的叶片数量为有限值，与上述理想情况下叶片数无穷的假设矛盾，导致尾流中的漩涡系发生改变，因此需要引入普朗特叶尖损失修正因子F对速度诱导因子进行修正：

(14)

(15)

式中：RWT为叶轮半径，m.

叶轮气动扭矩TWT为：

(16)

式中：Rh为轮毂半径，m.

1.3 风力机柔性传动链模型

风力机传动链将叶轮的扭矩传递到发电机，主要由主轴、齿轮箱、机械制动器、高速轴联轴器和轴承等组成，如图1所示.图1中将叶轮、齿轮箱和发电机等效为质量块，忽略齿轮箱、高速轴和机械制动器的柔性，主轴等效为弹簧和阻尼，忽略联轴器和轴承的影响.

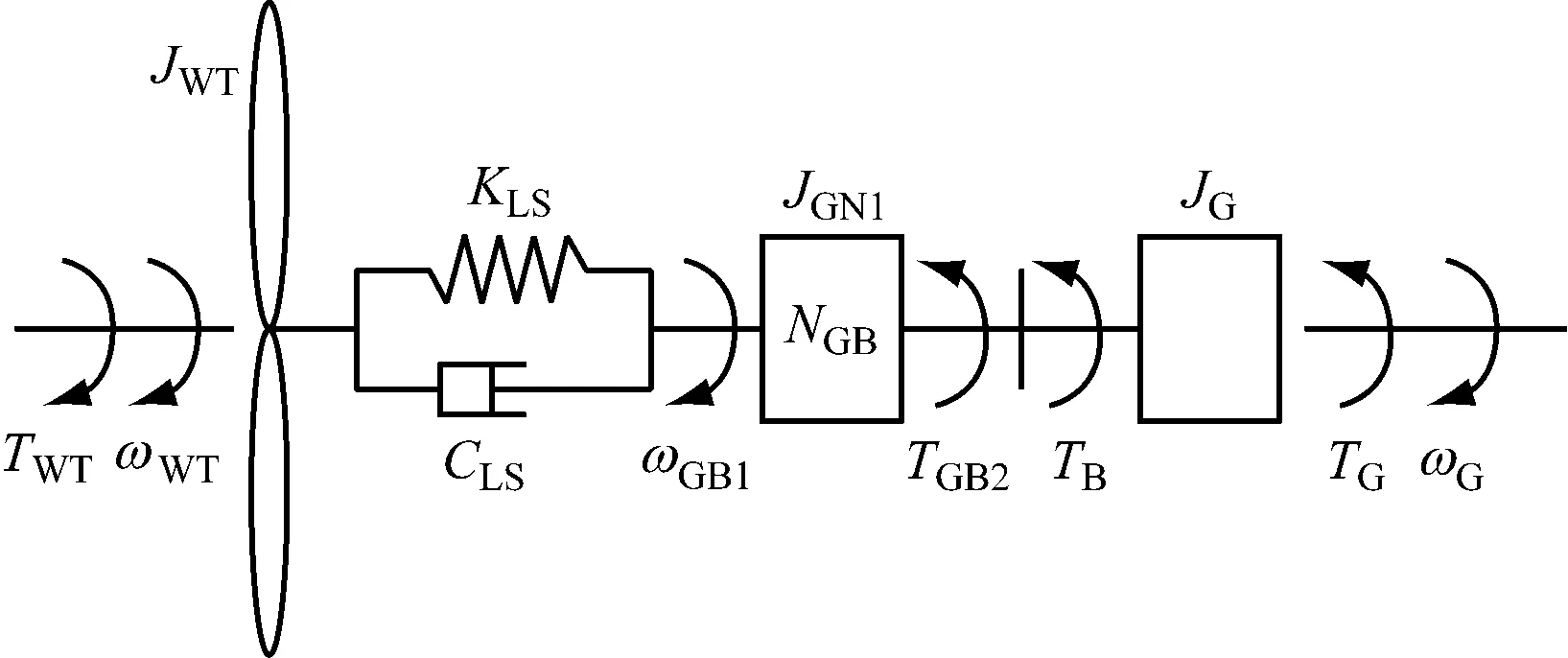
图1 传动链的物理模型

叶轮的动力学方程为：

(17)

式中：JWT为叶轮的转动惯量，kg·m2；TWT为叶轮气动扭矩，N·m；CLS为低速轴扭转阻尼，(N·m)/(rad·s-1)；KLS为低速轴扭转刚度，(N·m)/rad；ωGB1为齿轮箱输入端角速度，rad/s；θWT为叶轮扭转角，rad；θGB1为齿轮箱输入端扭转角，rad.

发电机的动力学方程为：

(18)

式中：JG为发电机转子的转动惯量，kg·m2；TG为发电机电磁反转矩，紧急制动时变为零，N·m；TB为机械制动力矩，正常运行时为零，N·m；TGB2为齿轮箱输出端力矩，N·m.

双馈异步感应发电机的电磁反转矩为[10]：

(19)

式中：nQ为极对数；Lm为定子转子互感系数，H；Ls为定子自感系数，H；Ψs为定子磁链，Wb；iqr为q轴转子电流，A.

机械制动力矩为：

(20)

式中：TB,max为最大机械制动力矩，N·m；t0为机械制动器投入的时刻.

齿轮箱的动力学方程为：

(21)

式中：JGB1为齿轮箱输入端等效转动惯量，kg·m2；NGB为齿轮箱传动比.

(22)

式中：Jj为齿轮箱第j个齿轮的转动惯量，kg·m2；N0j为齿轮箱第j个齿轮与齿轮箱输入端的传动比.

联立式(17)、式(18)和式(21)，得到齿轮箱输入端扭矩：

(23)

1.4 齿根弯曲应力模型

齿轮在每个啮合过程中，每个轮齿齿根上的载荷都经历从0到最大再到0的过程.齿轮每转一圈，每个轮齿则经历固定次数的脉动载荷循环.由于齿根疲劳裂纹在压应力下不扩展，因此可忽略齿轮箱输入扭矩中的负值.

齿轮箱行星轮级太阳轮的啮合力Fs为：

Fs=TGB1/(N0s×rbs×np)

(24)

式中：rbs为太阳轮的基圆半径，m.

齿根弯曲应力σF为[8]：

(25)

式中：αs为太阳轮压力角，(°)；Bs为太阳轮齿宽，mm；-mn为太阳轮模数，mm；YFα为齿形系数；YSα为应力修正系数；Yε为弯曲强度重合度系数；Yβ为弯曲强度螺旋角系数.

综合各个风速区间风速样本对应的齿根弯曲应力的幅值和循环次数，可得齿根弯曲疲劳载荷谱.

2 风力机齿轮齿根疲劳裂纹扩展模型

齿轮齿根疲劳裂纹如图2所示，根据断裂力学知识，裂纹尖端的应力场具有奇异性，其强度不能使用应力来表征，要使用应力强度因子来表征.裂纹前缘的应力强度因子K的计算公式为[8]：

(26)

式中：σF为齿根应力，MPa；Y为形状因子，是构件的形状尺寸、受力状态和裂纹形状尺寸的函数；a为裂纹长度，mm.

应力强度因子幅值为：

ΔK=Kmax-Kmin=Kmax-0

(27)

图2 齿轮齿根疲劳裂纹

式中：Kmax为极大应力强度因子，MPa·mm0.5；Kmin为极小应力强度因子，MPa·mm0.5.

疲劳裂纹的扩展速率与应力强度因子的幅值有关.根据应力强度因子的幅值与疲劳裂纹扩展门槛值ΔKth的关系、应力强度因子极大值与断裂韧性KC的关系，在双对数坐标下，疲劳裂纹扩展速率与应力强度因子幅值的关系可分为3个区域.

在区域Ⅰ，ΔK<ΔKth.此时疲劳裂纹扩展速率为0，裂纹不扩展.

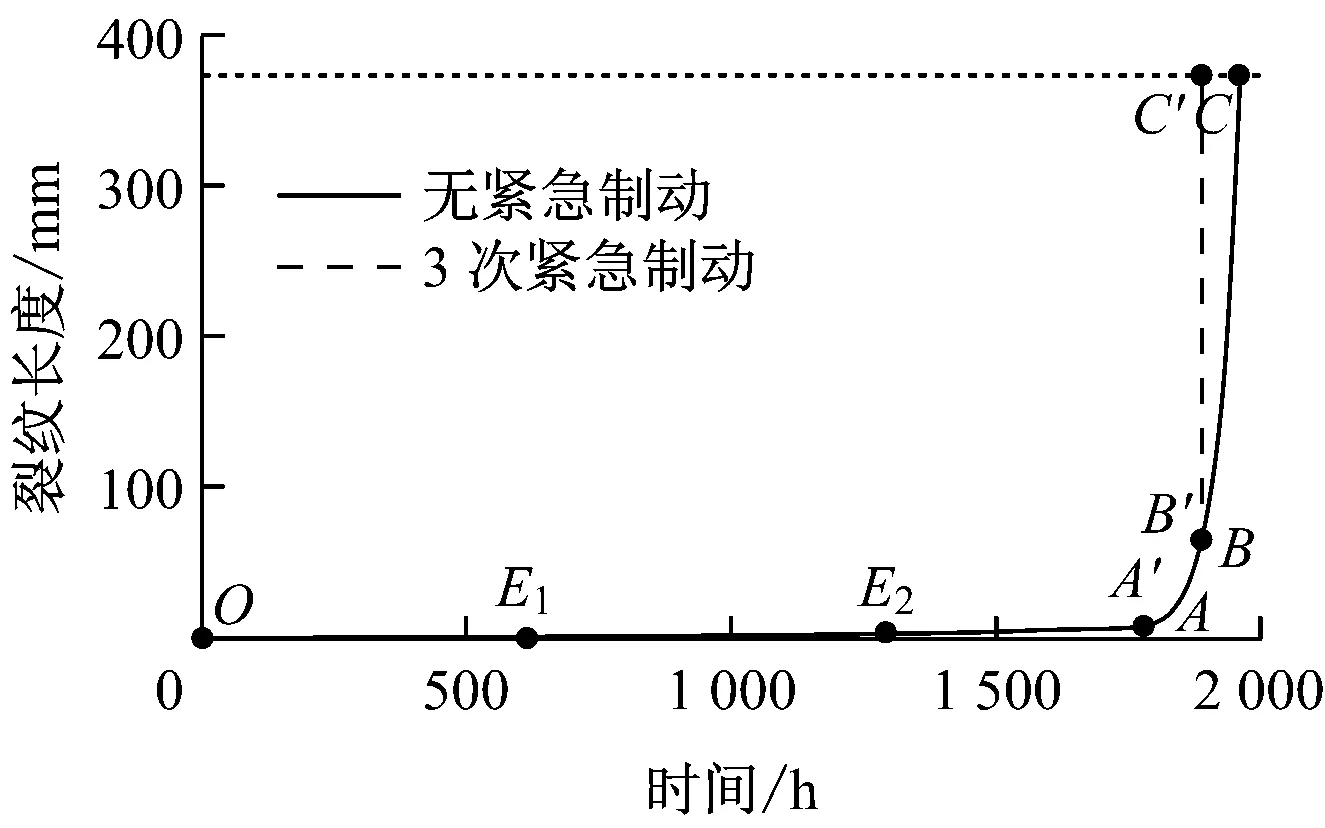
在区域Ⅱ，ΔK≥ΔKth，且Kmax

da/dN=ci(ΔK)ni

(28)

式中：da/dN为疲劳裂纹扩展速率，mm/循环；ci、ni为材料常数,可根据实验结果得到，下标i表示第i阶段，不同疲劳裂纹扩展阶段i值不同.

在区域Ⅲ，Kmax≥KC.此时疲劳裂纹扩展速率迅速增大，裂纹失稳扩展直到断裂.区域III的疲劳裂纹扩展寿命很短，一般计算中可忽略不计.

由式(26)可以看出，当应力恒定时，随着裂纹长度的增加，应力强度因子增大.当裂纹长度增加到某一值时，应力强度因子增大到等于断裂韧性，此时的裂纹长度称为临界裂纹长度.临界裂纹长度ac可通过式(26)反推求得：

(29)

由式(29)可以看出，当应力不恒定时，临界裂纹长度随应力的增大而变短，最短临界裂纹长度出现在最大应力作用时.

裂纹从初始裂纹长度a0扩展到临界裂纹长度ac所经历的循环数即为以循环数表示的疲劳裂纹扩展寿命.根据循环数与时间的对应关系，可求得以时间表示的疲劳裂纹扩展寿命.

在恒幅载荷作用下，已知初始裂纹长度a0，对式(27)直接积分，可求得疲劳裂纹扩展寿命N：

(30)

在变幅载荷作用下，应力强度因子幅值不仅与裂纹长度有关，也与应力大小有关.因此，在变幅载荷作用下，不能直接对Paris公式进行积分来求得疲劳裂纹扩展寿命.此时需要分别计算每次加载时的疲劳裂纹扩展长度，然后累加求得疲劳裂纹扩展量，最后求得疲劳裂纹扩展寿命.具体过程为：

第i次加载时，将加载载荷σFi和上次加载后的裂纹长度ai-1代入式(26)和式(28)，分别求得应力强度因子极大值Kmax,i和幅值ΔKi.当i=1时，裂纹长度ai-1=a0.

对比应力强度因子极大值Kmax,i与断裂韧性KC的大小，判断裂纹是否失稳扩展断裂.如果Kmax,i≥KC，则裂纹失稳扩展断裂，齿轮的疲劳裂纹扩展寿命为i-1次循环.

对比应力强度因子幅值ΔKi与疲劳裂纹扩展门槛值ΔKth的关系，判断裂纹是否扩展.若ΔKi<ΔKth，则裂纹不扩展，疲劳裂纹扩展长度Δai=0.

当裂纹稳定扩展时，疲劳裂纹扩展量Δai=c(ΔKi)n，加载后的裂纹长度ai=ai-1+Δai.

3 案例分析

以1.5 MW风力机齿轮箱行星级太阳轮为例，分析变风载作用下的齿轮疲劳裂纹扩展剩余寿命.风力机及太阳轮的基本参数分别见表1和表2.

表1 1.5 MW风力机基本参数[10]

表2 太阳轮参数[19]

风力机输入风速采用新疆达坂城风电场风力资源，平均风速为8.37 m/s，假设风速分布服从双参数威布尔分布，威布尔分布的尺度因子为9.409 1,形状因子为1.778 8[20]，使用Matlab威布尔随机数发生器生成各风速区间的运行风速样本.根据式(2)求得该风电场的理论年等效利用小时数为3 694.93 h，而达坂城风场的实际年等效利用小时数为2 051 h[21]，根据式(3)求得发电量综合折减系数为55.51%.根据式(4)～式(6)，得到各风速区间风力机太阳轮齿根弯曲应力的循环次数，如表3所示.

根据各风速区间的风速样本，使用叶轮气动力模型计算得到叶轮的气动力；将传动链动力学模型中的二阶微分方程组转换为一阶微分方程组，使用Matlab平台的ode45求解器对传动链的动力学模型进行求解，计算得到齿轮箱的输入力矩；根据齿根弯曲应力模型计算得到齿根弯曲应力幅值.综合各风速区间风力机齿根弯曲应力的幅值，得到其概率分布，如图3所示.由图3可以看出，齿根弯曲应力分布在0～165 MPa，这主要是由于在正常运行时，风力机的功率随风速的变化而变化，齿根弯曲应力也随之变化.齿根弯曲应力峰值出现在155 MPa附近，其对应的风速区间为风速区间10，说明齿根在额定工况下承受较大的弯曲应力.

图3 太阳轮齿根弯曲应力概率密度

风力机齿轮箱的最大瞬时极限载荷发生在紧急制动工况下.紧急制动停机时，发电机与电网断开，发电机的电磁反转矩瞬时变为0，气动刹车和高速轴机械刹车装置同时投入使用，其中气动刹车延迟时间为0.3 s，气动刹车最大顺桨速率为10 (°)/s，机械刹车延迟时间为0.9 s，根据文献[22]，最大机械制动力矩取23 800 N·m.当风速为25 m/s时，风力机紧急制动过程齿轮箱输入端的扭矩如图4所示，在第5 s，风力机开始紧急制动.紧急制动过程中，最大扭矩出现在紧急制动开始后的5.7 s，最大扭矩为2.15×106N·m，是额定输入扭矩的3.02倍，此时齿根弯曲应力达到最大值，为467.50 MPa.

图4 风力机紧急制动过程齿轮箱输入扭矩

假设太阳轮齿根表面存在一条中心裂纹，长度为a0=0.1 mm，考虑裂纹沿齿宽方向扩展，形状因子为Y=1.12[8].根据文献[18]，Paris公式中的系数为c1=5.67×10-12,n1=1.98,c2=2.09×10-11,n2=2.145；断裂韧性KC=5 183.81 MPa·mm0.5.根据式(29)，当考虑紧急制动导致的瞬时极限载荷时，得到最短临界裂纹长度为31.2 mm.

根据齿根疲劳裂纹扩展模型，以表2中的载荷作为输入载荷，假设风力机一年经历12次紧急制动，分别在不考虑紧急制动和考虑紧急制动时得到齿轮疲劳裂纹扩展结果，如图5所示.不考虑紧急制动时，疲劳裂纹扩展曲线为O—A—B—C；考虑紧急制动时，疲劳裂纹扩展曲线为O—A′—B′—C′，其中在E1点、E2点和B′点分别经历了一次紧急制动.

图5 疲劳裂纹扩展曲线

当不考虑紧急制动时，O—A为疲劳裂纹扩展第1阶段，历时1 777 h，在额定载荷下疲劳裂纹扩展速率缓慢增长至5.09×10-7mm/循环；A—C为疲劳裂纹扩展第2阶段，历时183 h，在额定载荷下疲劳裂纹扩展速率从5.09×10-7mm/循环快速增长直到断裂，疲劳裂纹扩展总寿命为1 960 h.

当考虑紧急制动时，O—A′为疲劳裂纹扩展第1阶段，历时1 777 h，在E1点和E2点分别经历一次紧急制动，最大载荷下的疲劳裂纹扩展速率分别为6.09×10-7mm/循环和3.05×10-6mm/循环，但由于较大载荷持续时间只有3 s左右，因此紧急制动对疲劳裂纹扩展长度的影响很小；A′—B′为疲劳裂纹扩展第2阶段，历时83 h，在额定载荷下疲劳裂纹扩展速率从5.09×10-7mm/循环快速增长至5.78×10-5mm/循环；B′—C′为裂纹失稳扩展阶段，由于在B′点经历了一次紧急制动，并且B′点裂纹长度超过最短临界裂纹长度，因此裂纹失稳扩展并断裂，疲劳裂纹扩展总寿命为1 860 h.

综上所述，在疲劳裂纹扩展第1阶段，紧急制动冲击对疲劳裂纹扩展的影响不大.在疲劳裂纹扩展第2阶段，紧急制动冲击对疲劳裂纹扩展的影响明显，使疲劳裂纹扩展寿命缩短了100 h.在整个疲劳裂纹扩展过程中，3次紧急制动冲击使疲劳裂纹扩展寿命缩短了约5.1%.

4 结 论

(1)在仅考虑风载荷作用的情况下，疲劳裂纹扩展剩余寿命为1 960 h.而当考虑3次紧急制动瞬时工况导致的极限载荷影响后，疲劳裂纹扩展剩余寿命缩短至1 860 h，比不考虑紧急制动时缩短了5.1%.

(2)紧急制动对疲劳裂纹扩展第1阶段的影响较小，而对疲劳裂纹扩展第2阶段影响显著.因此，在对风力机齿轮裂纹寿命进行预测时，紧急制动等冲击对疲劳裂纹扩展后期的影响不可忽视.

[2] SPINATO F,TAVNER P J,VAN BUSSEL G J W,et al.Reliability of wind turbine subassemblies[J].IET Renewable Power Generation,2009,3(4):387-401.

[3] ECHAVARRIA E,HAHN B,VAN BUSSEL G J,et al.Reliability of wind turbine technology through time[J].Journal of Solar Energy Engineering,2008,130(3):031005.

[4] 吴树梁.兆瓦级风电齿轮箱故障监测及分析[D].济南:山东大学,2012.

[5] 刘殷.风电齿轮箱设计计算中的材料热处理影响因素分析[J].机械传动,2010,34(6):68-72.

LIU Yin.Analysis of material & heat-treatment influence factors in design and calculation for wind turbine gearbox[J].Journal of Mechanical Transmission,2010,34(6):68-72.

[6] 王振雨,王乃祥,王继新,等.基于混合分布的齿轮载荷谱编制方法综述[J].矿山机械,2011,39(4):11-13.

WANG Zhenyu,WANG Naixiang,WANG Jixin,et al.Summarization on compilation of gear loading spectra based on mixed distribution[J].Mining & Processing Equipment,2011,39(4):11-13.

[7] 沈亮.齿轮疲劳寿命及齿根疲劳裂纹仿真分析[D].重庆:重庆大学,2011.

[8] 田雪.大型风电机组齿轮箱齿轮的疲劳寿命分析与预测[D].保定:华北电力大学,2014.

[9] 秦大同,张壮飞,周海波.随机风速下风力发电机传动系统动态外载荷计算[J].可再生能源,2012,30(9):21-26.

QIN Datong,ZHANG Zhuangfei,ZHOU Haibo.Dynamic loads calculation of wind turbines transmission system under random wind speeds[J].Renewable Energy Resources,2012,30(9):21-26.

[10] 张福平.变速变桨距风力发电机传动系统动态外载荷计算[D].重庆:重庆大学,2013.

[11] 武鑫,苏睿,芮晓明,等.新型并网风电机组的动力学建模与仿真[J].动力工程学报,2015,35(11):934-937,943.

WU Xin,SU Rui,RUI Xiaoming,et al.Dynamic modelling and simulation of a novel grid-connected wind turbine[J].Journal of Chinese Society of Power Engineering,2015,35(11):934-937,943.

[12] HEEGE A,RADOVCIC Y,BETRAN J.Fatigue load computation of wind turbine gearboxes by coupled structural,mechanism and aerodynamic analysis[J].DEWI Magazin,2006,28(2):61-68.

[13] SUN W,CHEN T,WEI J.Dynamic reliability of gears in a wind turbine gearbox under the conditions of variable wind speed and small samples[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2012,226(12):3032-3042.

[14] 祖世华.随机载荷下齿轮弯曲疲劳强度的研究[D].重庆:重庆工学院,2008.

[15] 周璇,蒋玮,刘华汉,等.风电齿轮齿根弯曲应力及裂纹特性分析[J].现代机械,2014(6):24-28.

ZHOU Xuan,JIANG Wei,LIU Huahan,et al.Bending stress and crack characteristics at the tooth root of a wind power gear[J].Modern Machinery,2014(6):24-28.

[16] 郭辰.风电场平均风速变化对利用小时数的影响研究[J].风能,2012(7):50-58.

GUO Chen.The effect of mean wind speed variations on equivalent available duration of wind farm[J].Wind Energy,2012(7):50-58.

[17] 杨娜.风力发电机组载荷建模与控制[D].北京:华北电力大学,2012.

[18] 陈健.大型行星齿轮减速齿轮断裂失效分析[D].沈阳:东北大学,2008.

[19] 方俊元.风力发电机组齿轮箱强度可靠性优化研究[D].保定:华北电力大学,2013.

[20] 包能胜,刘军峰,倪维斗,等.新疆达坂城风电场风能资源特性分析[J].太阳能学报,2006,27(11):1073-1077.

BAO Nengsheng,LIU Junfeng,NI Weidou,et al.Wind energy resource analysis at Dabancheng wind farm in Xinjiang region[J].Acta Energiae Solaris Sinica,2006,27(11):1073-1077.

[21] 史瑞静,李凤婷,樊小朝,等.风电场风电利用水平综合评价指标体系的研究分析[J].水力发电,2015,41(3):80-83,91.

SHI Ruijing,LI Fengting,FAN Xiaochao,et al.Study on comprehensive evaluation index system of wind power utilization level for wind farm[J].Water Power,2015,41(3):80-83,91.

[22] 孙明松,王江.1.5 MW风力发电机组液压刹车系统设计[J].科技与企业,2015(13):253.

SUN Mingsong,WANG Jiang.Design of hydraulic braking system of 1.5 MW wind turbine[J].Science and Technology and Enterprise,2015(13):253.

Residual Life Evaluation of Gear Root Crack Growth in Driving Train of a Wind Turbine

XIAOJunfeng,LIJianlan

(School of Energy and Power Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)

A calculation model for the residual life of gear root crack growth in driving train of a wind turbine was established at random wind speed on the basis of the impeller aerodynamic load model,the flexible driving train model and the gear root bending stress model,based on which the crack growth rate under random loads could be analyzed by calculating the gear root bending stress at different wind speeds.An analysis was conducted on the gear root crack growth of the sun gear in a 1.5 MW wind turbine.Results show that the residual life of gear root crack growth in a wind turbine is mainly affected by the wind load.Besides,the impact caused by emergency braking during later period of the crack growth can not be ignored.

wind turbine; gear; crack growth; emergency braking; residual life evaluation

2016-01-28

2016-04-07

国家自然科学基金资助项目(51375183)

肖俊峰(1990-)，男，重庆奉节人，硕士研究生，研究方向为风力机齿轮箱可靠性分析.李建兰(通信作者)，女，副教授，硕导，电话(Tel．)：13667290268；E-mail：hust_ljl@hust.edu.cn．

1674-7607(2017)01-0045-07

TK83

A 学科分类号：470.30