考虑层流分离的低速风力机翼型气动性能研究

唐新姿，黄轩晴，孙松峰，彭锐涛

(湘潭大学 机械工程学院，湖南湘潭 411105)

考虑层流分离的低速风力机翼型气动性能研究

唐新姿，黄轩晴，孙松峰，彭锐涛

(湘潭大学 机械工程学院，湖南湘潭 411105)

以风力机DU93-W-210翼型为研究对象，采用数值计算与实验验证方法研究了低雷诺数(2×105～5×105)下翼型升阻气动性能,基于修正转捩模型分析了多雷诺数多攻角下翼型层流分离泡对气动性能的影响.结果表明：基于四方程转捩模型Transition SST计算所得升阻力系数及翼型表面转捩位置与实验值接近，低雷诺数流动计算适用性较好；雷诺数越小，翼型层流分离泡越明显，翼型升阻比越小; 失速前雷诺数对翼型升阻比影响较大而失速后影响较小，且雷诺数越小该翼型失速越缓和；攻角越大，翼型上表面层流分离泡越靠近前缘而下表面越靠近尾缘; 失速前上表面和下表面转捩位置均呈线性变化，失速后上表面转捩位置呈非线性变化.

风力机翼型；低雷诺数；层流分离；气动性能；数值模拟

风力机翼型气动性能是影响风力机性能的关键因素，已受到国内外学者的广泛关注.低速风力机的性能主要取决于低雷诺数翼型气动性能，研究低雷诺数下风力机的翼型边界层流动与翼型气动性能，对中小型风力机性能分析和叶片优化设计有着重要意义.

对于风力机翼型气动性能研究而言，低雷诺数通常指的是雷诺数小于5×105，低雷诺数翼型边界层流动发生层流分离引起翼型气动性能剧烈变化[1].近年来，随着低速风力机与微型飞行器的发展，低雷诺数翼型气动性能研究受到越来越多的关注[2-3].如美国国家航空航天局(NASA)和伊利诺伊大学厄巴纳香槟分校(UIUC)等研究机构进行了很多实验和数值计算研究，研发了E387、SD7003等低雷诺数翼型[4-7].在风洞实验方面，Butterfield等[8]测试了S809翼型在雷诺数为3×105以上的一系列气动数据.Ananda等[9]通过开展风洞实验研究了低雷诺数(0.6×105～1.6×105)下准三维叶片展弦比和尖根比对气动性能的影响.黄宸武等[10]采用表面压力测量方式研究了在雷诺数小于5×105时，不同转捩条件和雷诺数下S809翼型的气动性能.低雷诺数风洞实验对湍流强度、展弦比和数据修正等较为敏感，有必要深入研究翼型边界层流动机理.如白鹏等[11]采用Rogers拟压缩方法求解不可压缩Navier-Stokes方程，研究了低雷诺数(6.0×104～2.0×105)条件下E387翼型在攻角为0°、4°和7°时上表面后缘部分的流动分离现象.靳允立等[12]采用基于Spalart-Allnaras(S-A)和SSTk-ω湍流模型的数值计算方法研究了翼型失速及雷诺数变化(1.0×104～1.0×106)对S809翼型的性能影响.Wata等[13-14]利用XFoil翼型分析软件设计并测试了适用于小型风力机的低雷诺数翼型.Counsil等[15]基于转捩模型研究了2种航空翼型NACA0012与SD7003在雷诺数为4.8×104～2.5×105、攻角为0°～8°时翼型转捩位置变化及升阻力特性.祖红亚等[16-17]采用XFoil软件和全湍流模型的数值计算方法研究了襟翼长度和尾缘修剪对翼型气动性能的影响.

上述研究多针对翼型的设计改进及雷诺数对翼型气动性能的影响，而对于考虑层流分离的低速风力机翼型多雷诺数、多攻角(包括失速前和失速后)下的气动性能影响研究相对较少.笔者以风力机专用翼型DU93-W-210为研究对象，采用基于修正转捩模型的数值计算与风洞实验验证相结合的方法，研究在不同雷诺数(2×105～5×105)和不同攻角(-3°～16°)下的翼型边界层流动分离变化规律，以及分离泡大小和位置对低雷诺数下风力机翼型升阻气动性能的影响，为中小型风力机叶片设计及流动控制提供参考.

1 数值计算方法

1.1 湍流模型

湍流模型方法主要分为雷诺平均法(RANS)、大涡模拟法(LES)和直接数值法(DNS)3大类.考虑到计算精度与计算资源要求的平衡，采用基于RANS方法，并分别采用湍流模型一方程模型S-A、两方程模型SSTk-ω和四方程转捩模型Transition SST求解翼型绕流场.

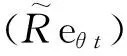
(1)

(2)

式中:ρ为密度；t为时间；uj为速度；j为张量中的自由标；xj为坐标值；θ为动量厚度；μ为层流黏性系数；μt为湍流黏性系数；Pγ、Eγ和Pθ t的具体形式可参阅文献[19]，方程常数σγ=1.0，σθ t=2.0.

当发生流动分离时，在分离泡处γ迅速增加，随着湍流黏性比的提高，γ的增加趋于平缓，因此专门为分离流转捩设计的间歇因子γsep可表示为

γsep=2Fθ t·min(1.0,FreattachRev，max)

(3)

(4)

式中：开关函数Fθ t的具体形式可参阅文献[19].

最终考虑分离情况的间歇因子可表示为

γeff=max(γ,γsep)

(5)

然后，将修正后的间歇因子γeff与SST湍流模型中的k方程耦合联合模拟转捩过程，转捩模型与SST湍流模型的结合控制方程为

(6)

其中，

(7)

式中：Pk、Dk分别为原SST湍流方程的生成项和耗散项；σk为k对应的湍流普朗特参数.

1.2 网格与边界条件

数值计算翼型外流域为二维C型，取翼型前方半径和宽度为15倍翼型弦长，翼型后方长度为20倍翼型弦长.边界如图1所示，流域进口abcde设置为速度进口，通过改变进口来流风速来改变雷诺数大小，速度方向由来流攻角确定；来流湍流强度为0.2%，湍流黏度比为10；流域出口a-f-e设置为压力出口，总压为101.325 kPa；翼型表面g-m-h-n-g满足壁面无滑移条件.采用基于压力算法和二阶迎风差分格式离散，Simple压力速度耦合双精度求解.非定常RANS计算物理时间推进步长为Δt，各计算收敛标准为残差小于1×10-5.Δt可表示为

(8)

式中：c为翼型弦长；V∞为进口来流风速大小.

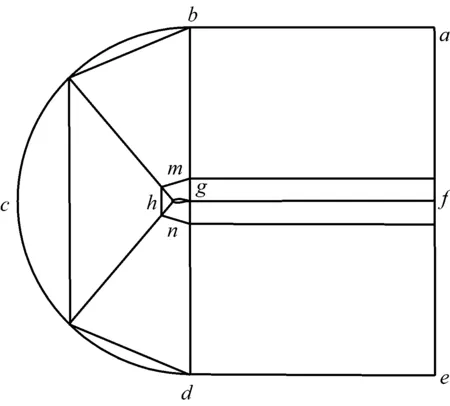
图1 二维流域拓扑结构

采用ICEM生成四边形网格，取物面法向第一层网格高度为10-5倍弦长，满足y+小于1.同时，兼顾网格纵横比翼型上下表面共分布376个网格节点，并对翼型周围网格进行局部加密，S809翼型和DU93-W-210翼型计算网格总数分别为91 024和99 719.流域计算网格如图2所示.

2 结果与分析

2.1 低雷诺数计算模型验证

为验证低雷诺数数值计算方法的正确性与转捩模型的适用性，采用3种不同湍流模型比较分析了在雷诺数为3×105时S809翼型的升阻气动性能，并与美国科罗拉多州州立大学(CSU)风洞实验值[8]进行比较，结果如图3所示.

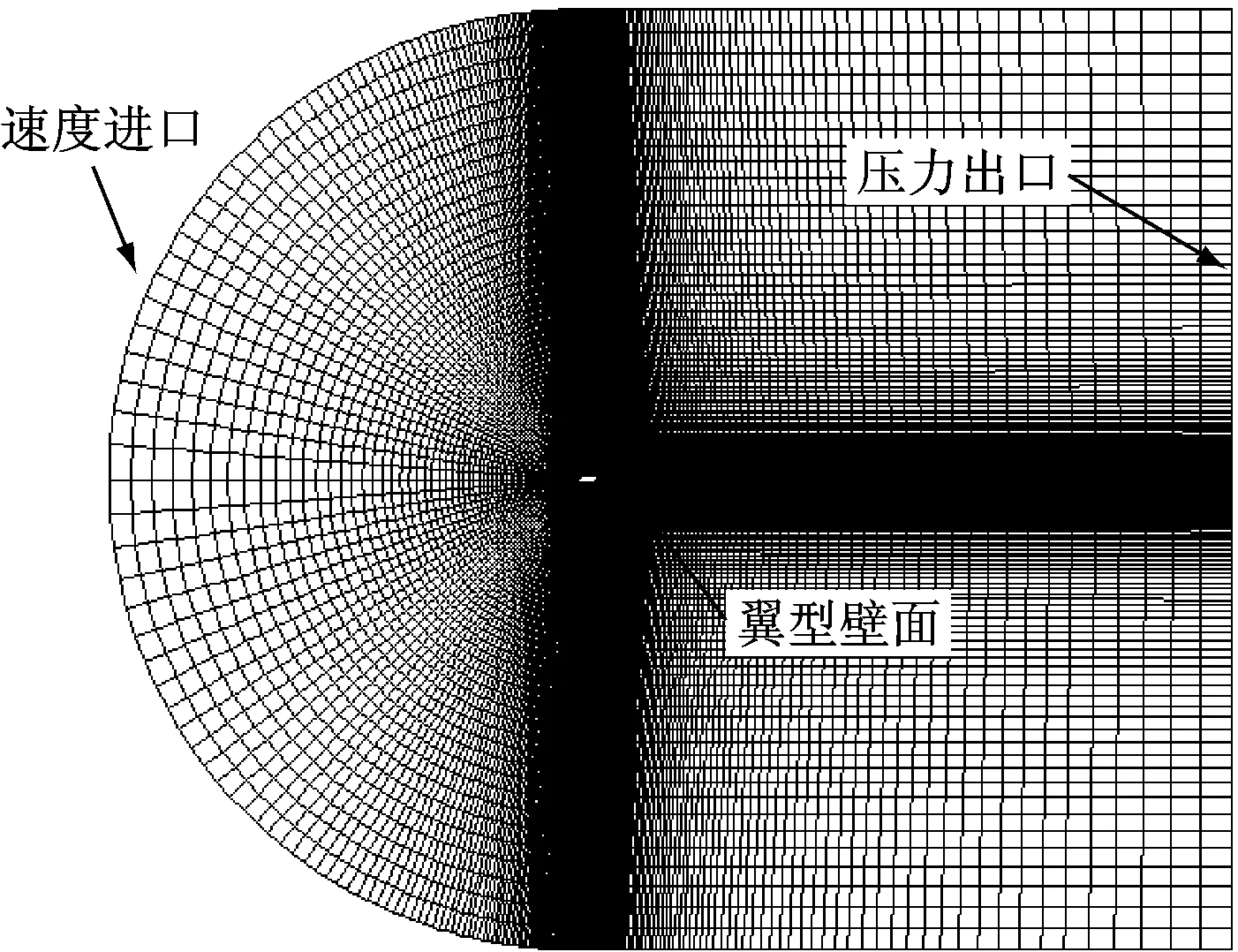
图2 DU93-W-210翼型计算网格

从图3(a)和图3(b)可以看出，3种湍流模型计算所得的升力系数与实验值吻合较好，变化趋势基本相同.在攻角较小时，3种湍流模型计算所得的升力系数基本一致，且与实验值基本吻合；而攻角较大时，升力系数计算值开始呈现波动趋势.这是因为攻角增大后，翼型边界层开始存在非定常流动，造成不同湍流模型预测的结果不一致.从图3(c)和图3(d)可以看出，与另外2种湍流模型相比，四方程转捩模型Transition SST计算所得的升力系数稍大而阻力系数较小，说明在低雷诺数层流状态下，摩擦阻力影响更大.同时，由于四方程转捩模型Transition SST加入了额外的两变量运输方程来捕捉层流分离与转捩过程，计算收敛所需时间较其他湍流模型所需时间长，但计算结果更接近实验值，因此，对于低雷诺数流动四方程转捩模型Transition SST更适用.

2.2 雷诺数对DU93-W-210翼型气动性能的影响

采用四方程转捩模型Transition SST对雷诺数分别为2×105、3×105、5×105和1×106时DU93-W-210翼型的气动性能进行比较计算，并与文献[20]的风洞实验数据进行比较，结果见图4，各计算收敛标准为残差小于1×10-5.由图4(a)可知，随着雷诺数的增大，该翼型升力系数Cl幅值逐渐增大，而图4(b)则显示阻力系数Cd随着雷诺数的增大而减小.同时，如图4(c)和图4(d)所示，该翼型升阻比Cl/Cd随着雷诺数的减小急剧降低，而最大升阻比对应的攻角略有增大.当攻角增大发生失速后，雷诺数对升阻比的影响逐渐减弱，且雷诺数越小该翼型失速特性越缓和.

2.3 DU93-W-210翼型边界层分离泡的影响

为研究边界层分离泡对DU93-W-210翼型气动性能的影响，采用四方程转捩模型TransitionSST对低雷诺数(2×105～5×105)、攻角为-3°～16°的翼型边界层速度分布和压力分布进行深入分析，结果如图5～图8所示，各计算收敛标准为残差小于1×10-5.

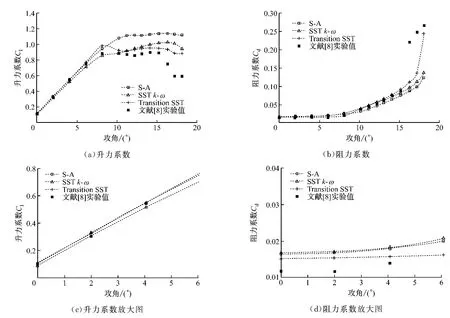
图3 S809翼型不同湍流模型的计算值与实验值的对比(Re=3×105)

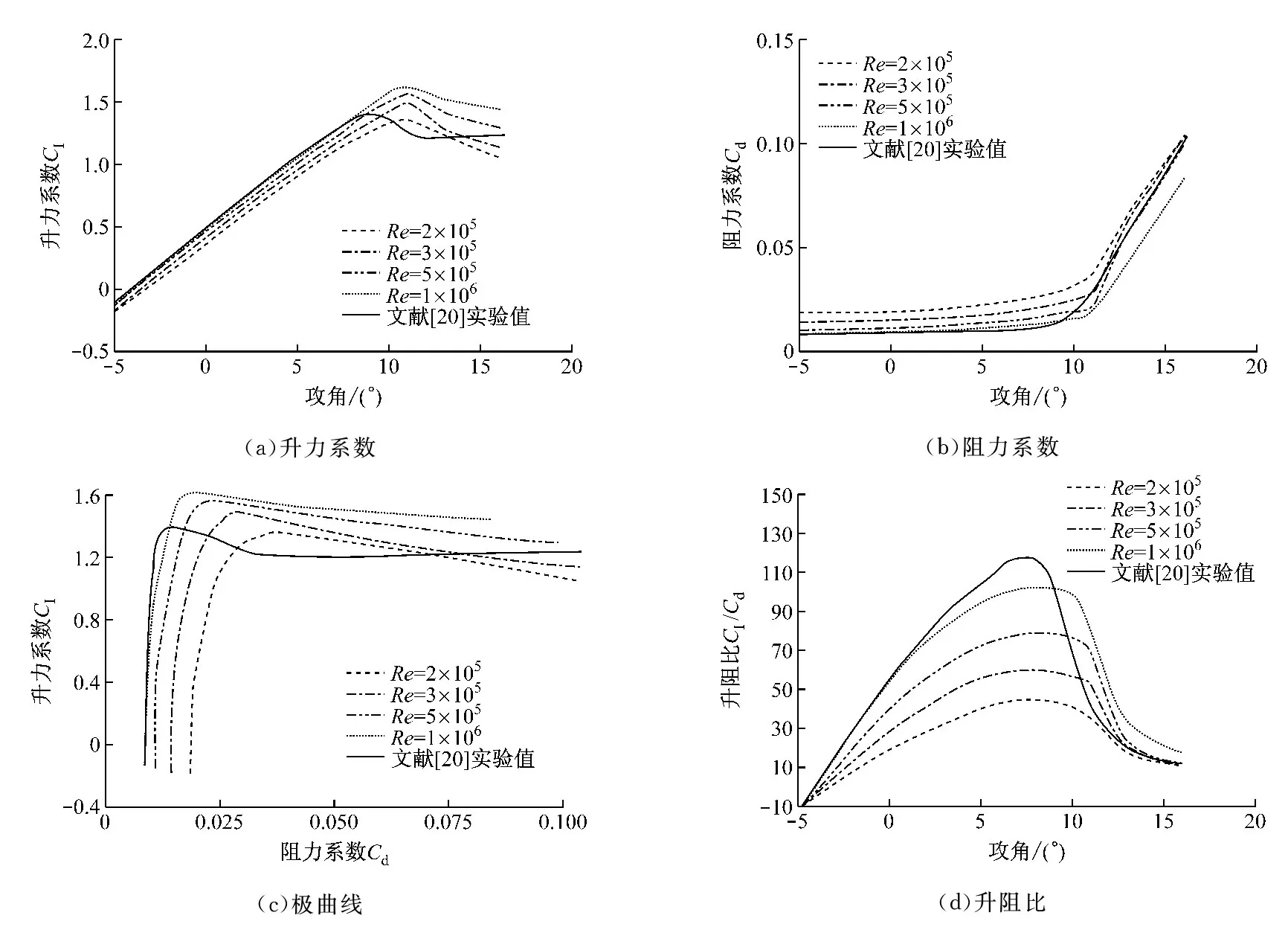
图4 不同雷诺数下DU93-W-210翼型气动性能曲线

由图5和图6(其中Cp为压力系数)可知，雷诺数为2×105时不同攻角下的上下翼型表面边界都存在尺度较明显的细长分离泡.这是由于在低雷诺数流动情况下，翼型边界层流动常处于层流状态，其抵抗逆压梯度的能力较弱，容易产生分离、转捩等流动现象.而随着攻角的增大，上下翼型表面的分离泡位置和大小都发生了改变，翼型上表面分离泡位置前移，而翼型下表面分离泡位置后移，且与图6翼型表面压力分布变化基本一致.这是由于翼型绕流发生分离后形成分离泡，分离泡影响了翼型表面的压力分布，进而对翼型的升阻力系数以及风力机叶片的气动性能等产生影响.当攻角增大到失速发生之后，尾缘气流分离变剧烈，雷诺数对阻力系数的影响相对减小.

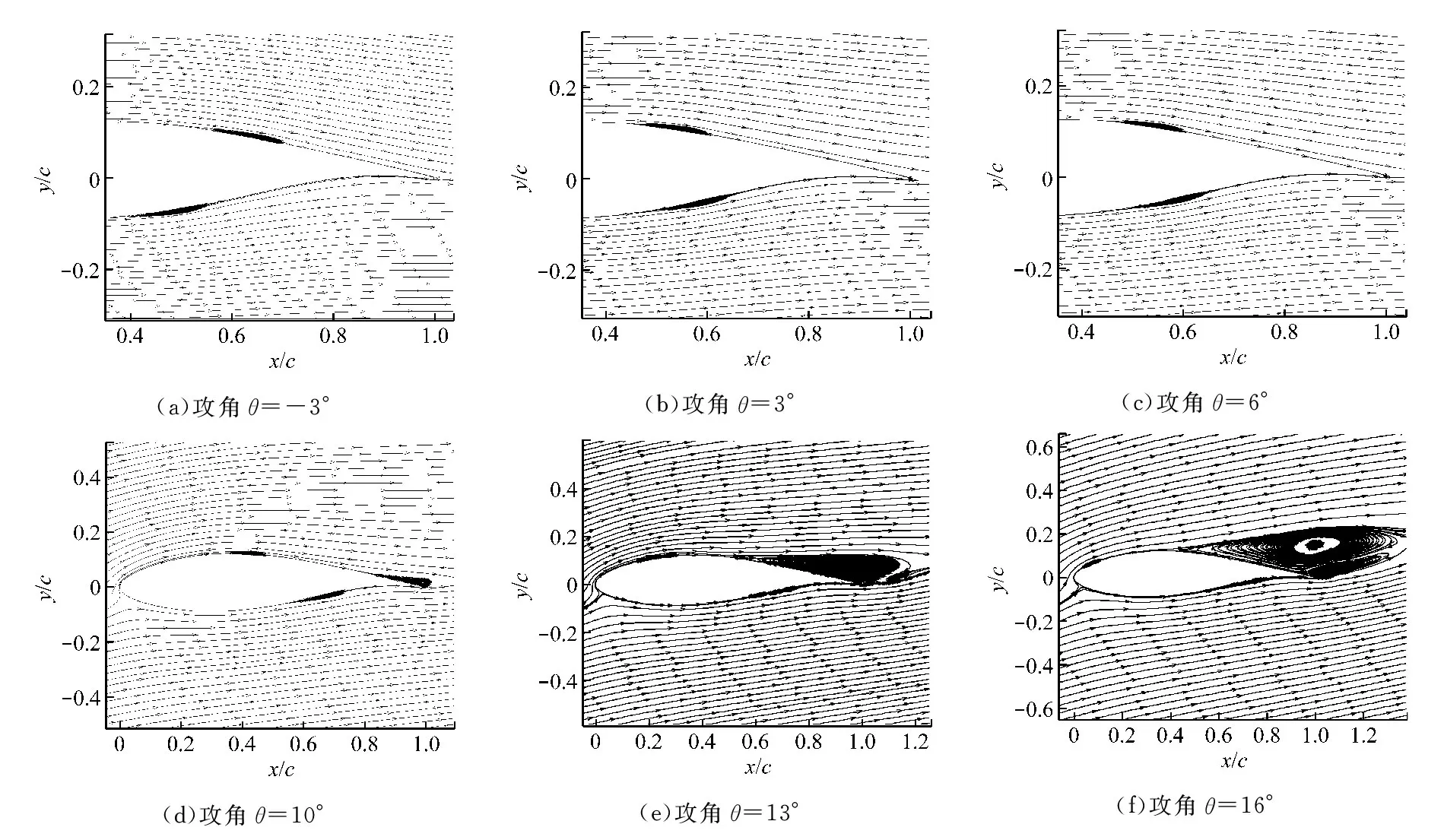
图5 不同攻角下的速度流线图(Re=2×105)

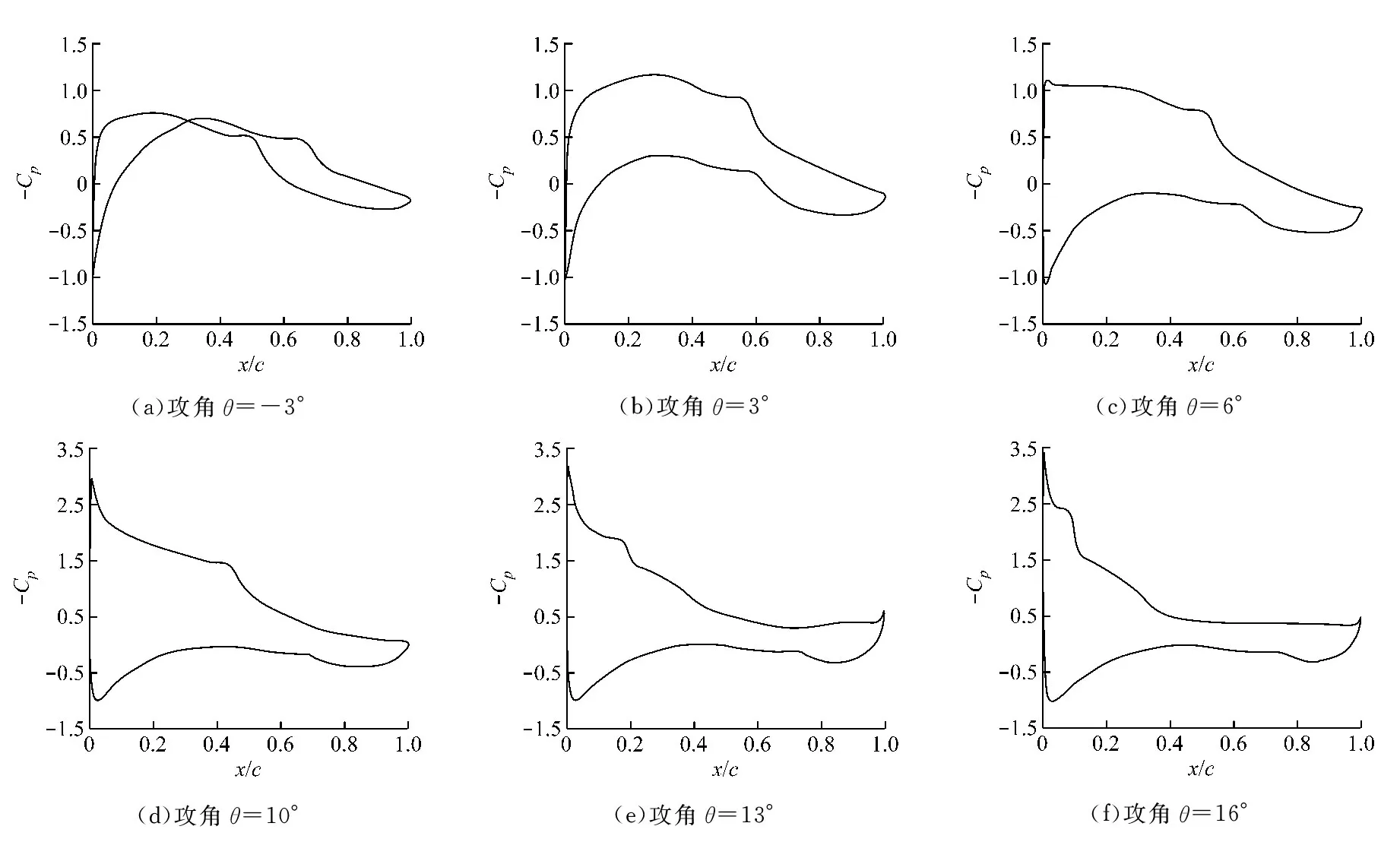
图6 不同攻角下翼型表面压力分布图(Re=2×105)

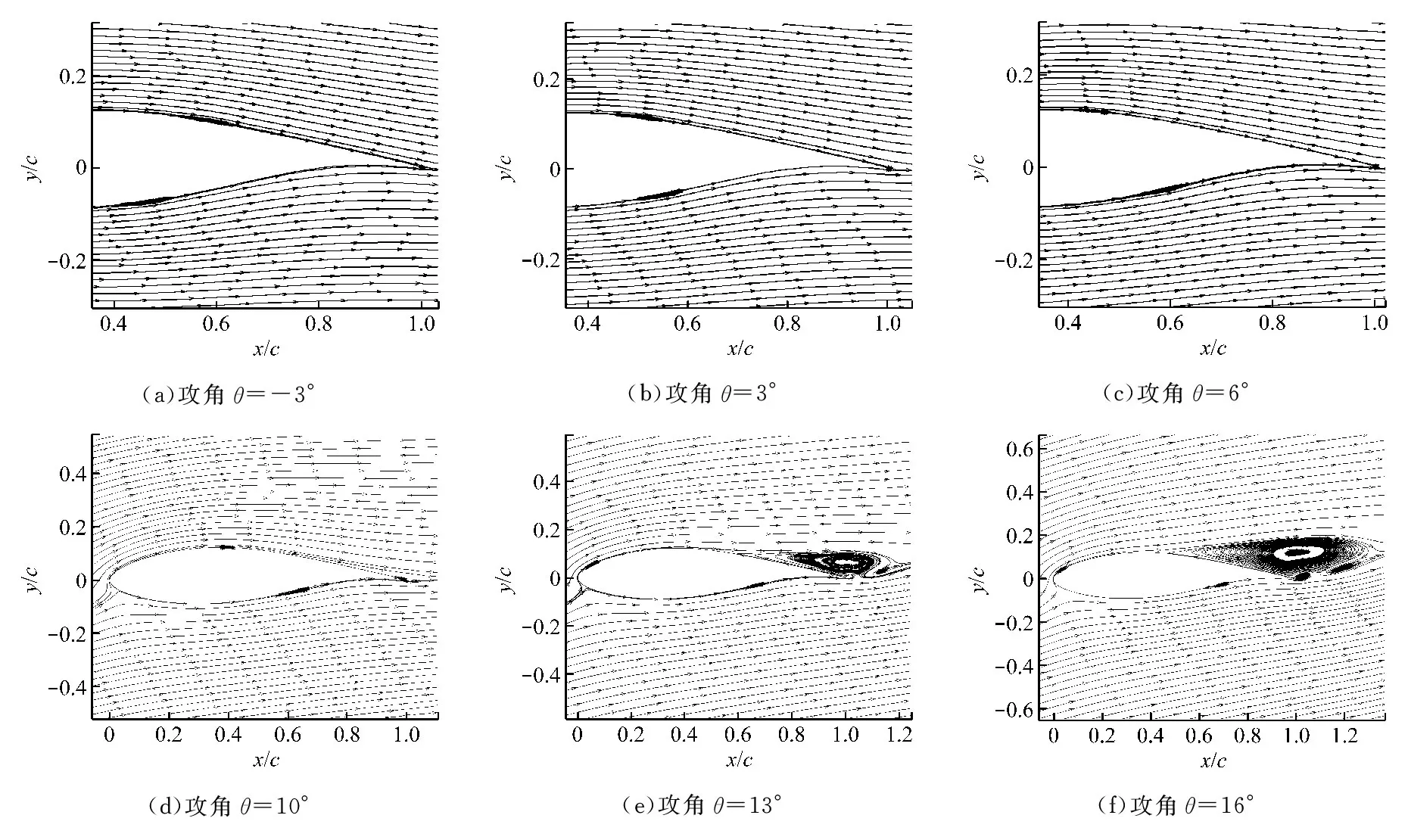
图7 不同攻角下的速度流线图(Re=5×105)

图8 不同攻角下翼型表面压力分布图(Re=5×105)

从图7和图8可以看出雷诺数为5×105时，不同攻角下的上下翼型表面边界层速度分布与压力分布，此时分离泡变小.从图5与图7可以看出，同一攻角时，雷诺数越小，翼型上下表面层流分离泡弦向分离跨度越大，分离泡越厚；对比图4(b)得出，低雷诺数翼型阻力上升主要由于翼型表面层流分离更明显.对比图6和图8可以看出，雷诺数越大，翼型表面压力分布越光滑，表明此时黏性边界层流动影响减小，其抵抗逆压梯度能力增强，因而升力系数增大，阻力系数减小，与图4结果一致.

2.4 DU93-W-210翼型转捩位置的预测

层流向湍流的转捩处表面摩阻系数会突然增大，这是判断转捩与否的重要依据.翼型表面摩阻系数分布图中摩阻系数突然增大的位置就是转捩点.如图9所示，S809翼型在攻角为1.02 °时，计算所得翼型上表面摩阻系数Cf在弦长0.55处显著增大，表明该处发生转捩，该转捩位置与文献[21]一致.同时，将S809翼型转捩位置的计算值与实验值[22]进行比较(见表1).从表1可以看出，采用四方程转捩模型Transition SST预测的转捩位置与实验值接近.

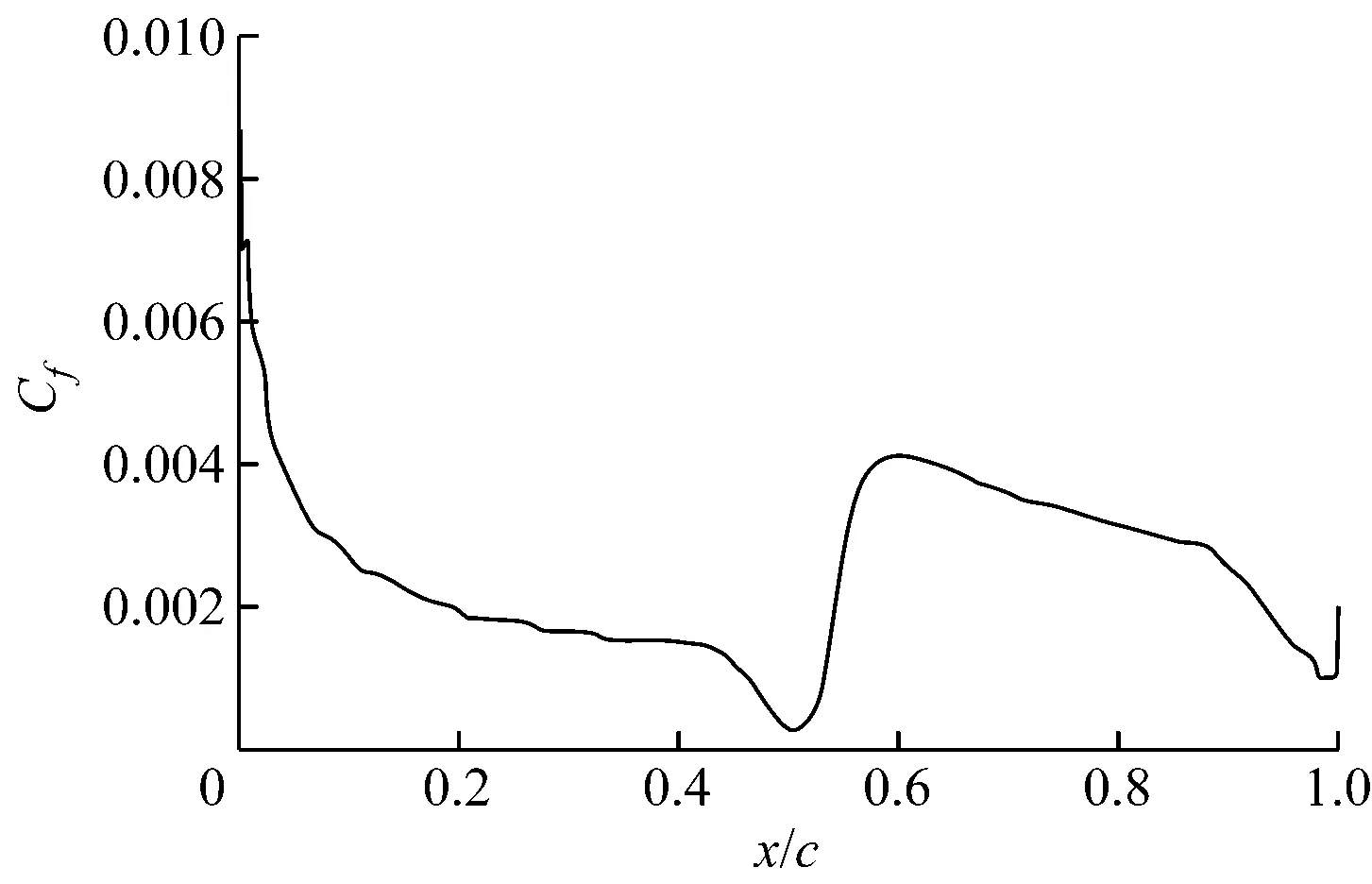
图9 攻角为1.02 °时S809翼型上表面摩阻系数

攻角/(°)实验转捩点(x/c)预测转捩点(x/c)上表面下表面上表面下表面1.020.550.500.500.475.130.500.520.500.487.990.070.520.050.499.960.030.540.010.50

图10给出了不同雷诺数和攻角下DU93-W-210翼型上下表面转捩位置在弦长方向的变化.由图10可知，雷诺数越大，上表面转捩位置越靠近前缘而下表面转捩位置越靠近尾缘.随着攻角的增大，不同雷诺数下上表面转捩位置均向翼型前缘移动，而下表面转捩位置均向尾缘移动.翼型失速前，上表面和下表面的转捩位置均呈线性变化；翼型失速后，上表面转捩位置呈非线性变化.当雷诺数为2×105，攻角小于10°时，上表面转捩位置在30%c～60%c处，攻角大于10°时，上表面转捩点迅速前移，在16°攻角时达到前缘4%c处；当雷诺数为5×105，同样在攻角为10°左右时上表面转捩点迅速前移，在大攻角失速后上表面转捩位置接近前缘而下表面更接近尾缘.这与图5和图7中分离泡位置的变化相吻合，也与文献[15]结论一致.

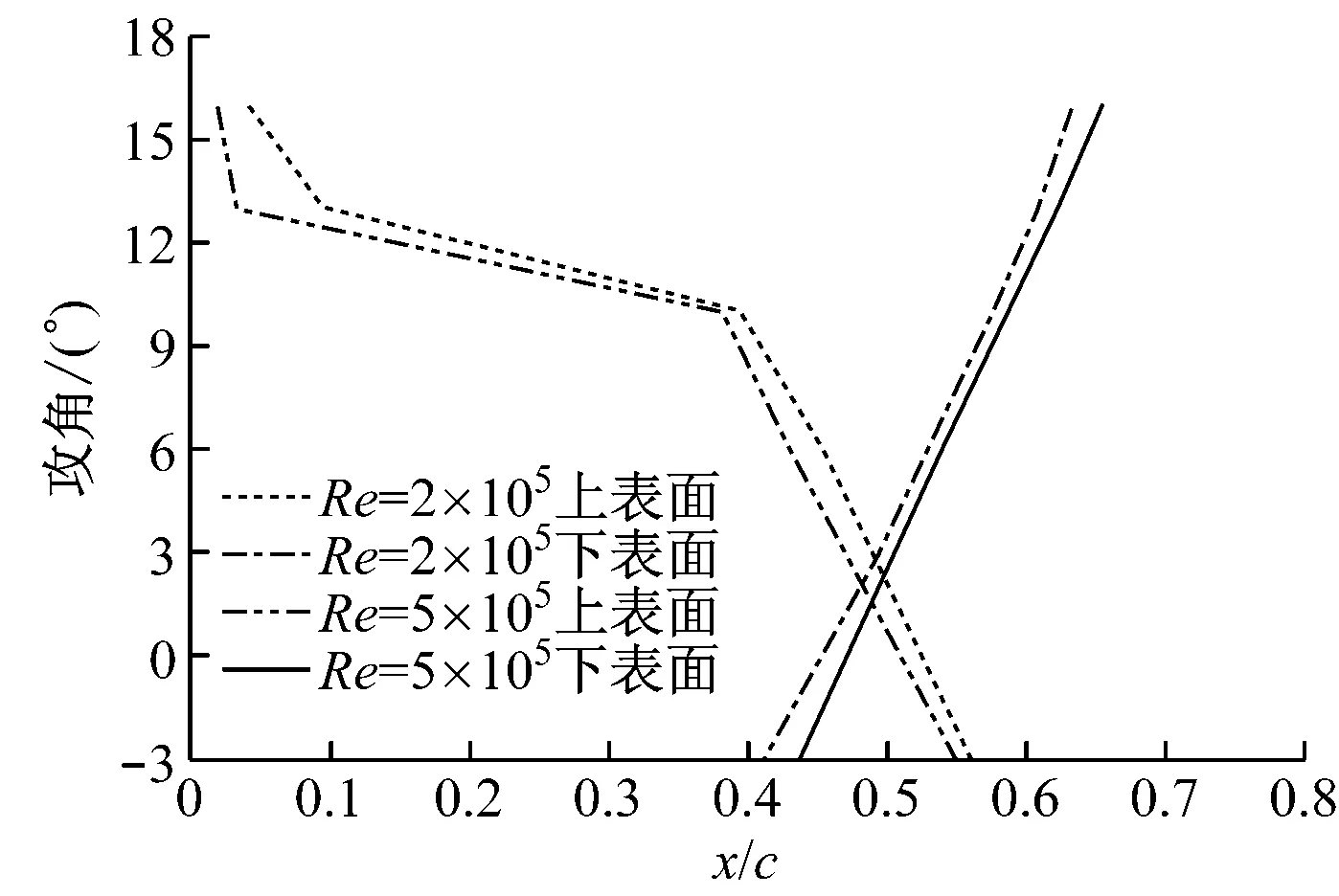
图10 DU93-W-210翼型表面转捩位置随攻角的变化

3 结 论

(1)四方程转捩模型Transition SST计算所得升、阻力系数与实验值吻合较好，且能够捕捉低雷诺数翼型表面层流分离泡，低雷诺数流动计算适用性较好.

(2)随着雷诺数的减小，DU93-W-210翼型升力系数减小而阻力系数增大，升阻比Cl/Cd急剧降低；同时，随着雷诺数减小最大升阻比对应的攻角略有增大，翼型发生失速后，雷诺数对升阻比的影响逐渐减弱，且雷诺数越小该翼型失速越缓和.

(3)雷诺数越小，翼型表面层流分离泡越明显；攻角越大，翼型上表面层流分离泡越靠近翼型前缘而下表面分离泡越靠近尾缘.翼型失速前上表面和下表面转捩位置均呈线性变化，翼型失速后上表面转捩位置急剧前移且呈非线性变化.翼型表面层流分离泡产生位置和大小影响低雷诺数阻力上升幅度.低雷诺数翼型升阻气动性能和层流分离泡的预测为低速风力机叶片设计与流动控制提供了依据.

[2] KIM D H,CHANG J W.Low-Reynolds-number effect on the aerodynamic characteristics of a pitching NACA0012 airfoil[J].Aerospace Science and Technology,2014,32:162-168.

[3] MALDONADO V,CASTILLO L,THORMANN A,et al.The role of free stream turbulence with large integral scale on the aerodynamic performance of an experimental low Reynolds number S809 wind turbine blade[J].Journal of Wind Engineering and Industrial Aerodynamics,2015,142:246-257.

[4] SELIG M S,GUGLIELMO J J,BROERN A,et al.Experiments on airfoils at low Reynolds numbers[C]//AIAA 34th Aerospace Sciences Meeting and Exhibit.Reno,USA:American Institute of Aeronautics and Astronautics,Inc.,1996.

[5] LIN J C M,PAULEY L L.Low-Reynolds-number separation on an airfoil[J].AIAA Journal,1996,34(8):1570-1577.

[6] CATALANO P,TOGNACCINI R.Turbulence modeling for low-Reynolds-number flows[J].AIAA Journal,2010,48(8):1673-1685.

[7] KOJIMA R,NONOMURA T,OYAMA A,et al.Large-eddy simulation of low-Reynolds-number flow over thick and thin NACA airfoils[J].Journal of Aircraft,2013,50(1):187-196.

[8] BUTTERFIELD C P,MUSIAL W P,SIMMS D A.Combined experiment phase I.Final report[R].Golden,Colorado，USA:NREL,1992.

[9] ANANDA G K,SUKUMAR P P,SELIG M S.Measured aerodynamic characteristics of wings at low Reynolds numbers[J].Aerospace Science and Technology,2015,42:392-406.

[10] 黄宸武,杨科,廖猜猜,等.S809风力机专用翼型低雷诺数气动性能实验研究[J].工程热物理学报,2014,35(11):2197-2201.

HUANG Chenwu,YANG Ke,LIAO Caicai,et al.Experimental study on aerodynamic characteristics of S809 dedicated wind turbine airfoil at low Reynolds numbers[J].Journal of Engineering Thermophysics,2014,35(11):2197-2201.

[11] 白鹏,崔尔杰,周伟江,等.翼型低雷诺数层流分离泡数值研究[J].空气动力学学报,2006,24(4):416-424.

BAI Peng,CUI Erjie,ZHOU Weijiang,et al.Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J].Acta Aerodynamica Sinica,2006,24(4):416-424.

[12] 靳允立,胡骏.翼型失速及雷诺数变化对风力机气动性能影响的数值研究[J].太阳能学报,2009,30(9):1280-1285.

JIN Yunli,HU Jun.Numerical research of the influence of airfoil stall and Reynolds number change on wind turbine aerodynamic performance[J].Acta Energiae Solaris Sinica,2009,30(9):1280-1285.

[13] WATA J,FAIZAL M,TALU B,et al.Studies on a low Reynolds number airfoil for small wind turbine applications[J].Science China Technological Sciences,2011,54(7):1684-1688.

[14] SINGH R K,AHMED M R.Blade design and performance testing of a small wind turbine rotor for low wind speed applications[J].Renewable Energy,2013,50:812-819.

[15] COUNSIL J N N,BOULAMA K G.Low-Reynolds-number aerodynamic performances of the NACA 0012 and Selig-Donovan 7003 airfoils[J].Journal of Aircraft,2013,50(1):204-216.

[16] 祖红亚,李春,李润杰,等.襟翼相对长度对翼型气动性能的影响[J].动力工程学报,2015,35(8):666-673,692.

ZU Hongya,LI Chun,LI Runjie,et al.Effect of relative flap length on aerodynamic performance of the airfoil[J].Journal of Chinese Society of Power Engineering,2015,35(8):666-673,692.

[17] 叶舟,郝文星,祖红亚,等.尾缘修剪对风力机翼型气动性能的影响[J].动力工程学报,2015,35(7):593-598,604.

YE Zhou,HAO Wenxing,ZU Hongya,et al.Influence of trailing edge trim on aerodynamic performance of the wind turbine airfoil[J].Journal of Chinese Society of Power Engineering,2015,35(7):593-598,604.

[18] MENTER F R,LANGTRY R B,LIKKI S R,et al.A correlation-based transition model using local variables-part I:model formulation[J].Journal of Turbomachinery,2006,128(3):413-422.

[19] LANGTRY R B,MENTER F R.Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J].AIAA Journal,2009,47(12):2894-2906.

[20] TIMMER W A,van ROOIJ R P J O M.Summary of the delft university wind turbine dedicated airfoils[J].Journal of Solar Energy Engineering,2003,125(4):488-496.

[21] 钟伟,王同光,王强.转捩对S809翼型气动性能影响的数值模拟[J].太阳能学报,2011,32(10):1523-1527.

ZHONG Wei,WANG Tongguang,WANG Qiang.Numerical Simulation of transition effect on aerodynamic performance of aerofoil S809[J].Acta Energiae Solaris Sinica,2011,32(10):1523-1527.

[22] SOMERS D M.Design and experimental results for the S809 airfoil[R].Colorado,USA:National Renewable Energy Laboratory,1997.

Study on Aerodynamic Characteristics of Low-speed Wind Turbine Airfoil in Consideration of Laminar Separation

TANGXinzi,HUANGXuanqing,SUNSongfeng,PENGRuitao

(School of Mechanical Engineering,Xiangtan University,Xiangtan 411105,Hunan Province,China)

The aerodynamic characteristics of DU93-W-210 wind turbine airfoil were studied at low Reynolds numbers (2×105-5×105) through numerical simulation and experimental tests,so as to analyze the effect of laminar separation bubble on the airfoil aerodynamic characteristics using corrected transition model at different Reynolds numbers and different angles of attack.Results show that the corrected Transition SST turbulence model predicts the lift and drag coefficients as well as the transition location well compared to experimental results at low Reynolds numbers; the lower the Reynolds number is,the more obvious the laminar separation bubble and the smaller the lift-drag ratio will be; the effect of Reynolds number on the lift-drag ratio of airfoil is evident but less obvious when stall exists,and the stall is softer at lower Reynolds numbers; at larger angles of attack,the laminar separation bubble on the upper surface of airfoil is closer to the leading edge,while that on the lower surface is closer to the trailing edge; the transition position on the lower and upper surface both moves in a linear manner before stall,and the transition position on the upper surface moves in a non-linear manner after stall.

wind turbine airfoil; low Reynolds number; laminar separation; aerodynamic characteristic; numerical simulation

2016-02-22

2016-04-06

国家自然科学基金资助项目(51305377，51375417)

唐新姿(1981-)，女，副教授，博士，主要从事叶轮机械气动力学方面的研究.电话(Tel．)：15173269528；E-mail：xinzitang@163.com.

1674-7607(2017)01-0052-08

TK83

A 学科分类号：480.60