二项分布常见考点举隅

崔 文 侯宇虹

(山东省文登第一中学 26440)

侯宇虹，中学高级教师，文登区教学能手，从事高中数学解题研究.

判断一个随机变量是否服从二项分布，关键有两点：一是对立性，即一次试验中，事件发生与否两者必有其一；二是重复性，即试验独立重复地进行了n次．

考点1：计算概率

例1 (1)将一枚均匀的硬币抛掷6次，则正面出现的次数比反面出现的次数多的概率为____．

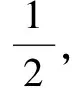
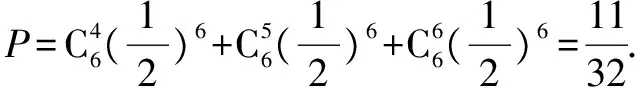
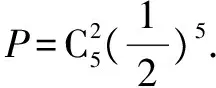
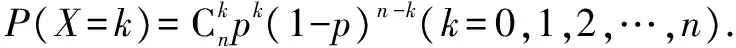
考点2：计算相关参数

例2 (1)在4次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生两次的概率，则事件A在一次试验中发生的概率p的取值范围是____.

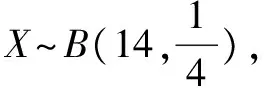
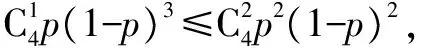
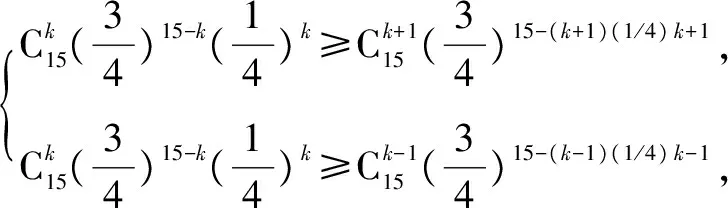
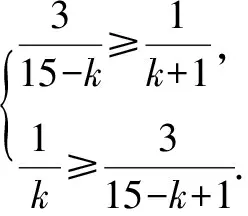
故k=3或4，故填3或4.

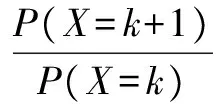
考点3：写出分布列

例3 投到某杂志的稿件，先由两位初审专家进行评审．若能通过两位初审专家的评审，则予以录用；若两位初审专家都未予通过，则不予录用；若恰能通过一位初审专家的评审，则再由第三位专家进行复审，若能通过复审专家的评审，则予以录用，否则不予录用．设稿件能通过各初审专家评审的概率均为0.5，复审的稿件能通过评审的概率为0.3.各专家独立评审．

(1)求投到该杂志的1篇稿件被录用的概率；

(2)记X表示投到该杂志的4篇稿件中被录用的篇数，求X的分布列．

解析(1)记A表示事件：稿件能通过两位初审专家的评审；

B表示事件：稿件恰能通过一位初审专家的评审；

C表示事件：稿件能通过复审专家的评审；

D表示事件：稿件被录用．

则D=A+BC，

而P(A)=0.5×0.5=0.25，P(B)=2×0.5×0.5=0.5，P(C)=0.3

故P(D)=P(A+BC)=P(A)+P(B)·P(C)=0.25+0.5×0.3=0.4.

(2)随机变量X服从二项分布，即X～B(4,0.4)，

X的可能取值为0,1,2,3,4，且

P(X=0)=(1-0.4)4=0.1 296,

P(X=4)=0.44=0.0 256.

故其分布列为

X01234P0．12960．34560．34560．15360．0256

评注首先要分析出X服从二项分布，然后结合公式求解即可．特别强调运算的准确性，分布列写完后，要注意检验分布列中概率和为1.

考点4：计算数学期望和方差

例4 (1)已知随机变量X服从二项分布B(n，p)．若E(X)=30，D(X)=20，则p=____.

(2)若X～B(n，p)，且E(X)=6，D(X)=3，则P(X=1)的值为( ).

A．3×2-2B．2-4C．3×2-10D．2-8

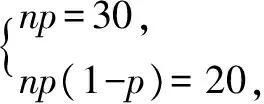
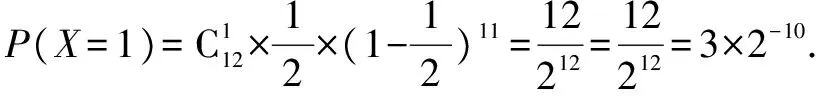
评注若X～B(n，p)，则E(X) =np，D(X)=np(1-p)．此公式需要熟练记忆.

考点5：交汇考查

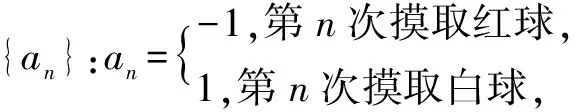
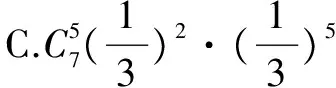
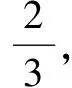
评注本例与数列交汇考查，只要分析出“S7=3”包含的基本事件，并且知道试验为“独立重复试验”即可.

考点6：综合运用

例6 某商场举行有奖促销活动，顾客购买一定金额的商品后即可抽奖．每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球．在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖．

(1)求顾客抽奖1次能获奖的概率；

(2)若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为X，求X的分布列和数学期望．

解析(1)记事件A1={从甲箱中摸出的1个球是红球}，A2={从乙箱中摸出的1个球是红球}，B1={顾客抽奖1次获一等奖}，B2={顾客抽奖1次获二等奖}，C={顾客抽奖1次能获奖}．

由题意，A1与A2相互独立，A1A2与A1A2互斥，B1与B2互斥，且B1=A1A2，B2=A1A2+A1A2，C=B1+B2.

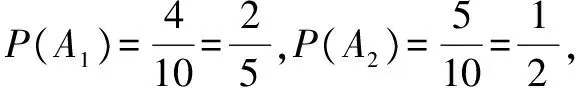
P(B2)=P(A1A2+A1A2)=P(A1A2)+P(A1A2)

=P(A1)P(A2)+P(A1)P(A2)

=P(A1)(1-P(A2))+(1-P(A1))P(A2)

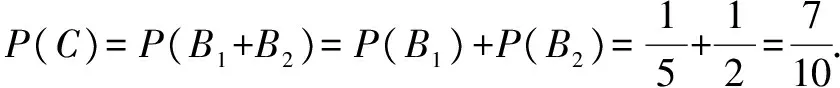
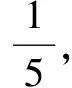
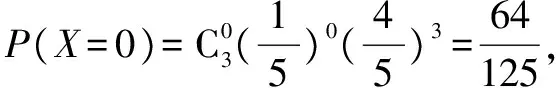
故X的分布列为

X0123P6412548125121251125

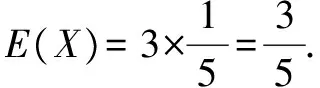
评注高考中二项分布题目要么以小题的形式出现，要么作为解答题的一部分出现.在解答题中，数学期望和方差一般套用公式直接计算.

[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2003.

[2]人民教育出版社课程教材研究所，中学数学课程教材实验研究组.普通高中课程标准实验教科书《数学》(选修2-3)[M].北京：人民教育出版社，2007(04).