单摆周期公式的应用及解题探讨

李乐薇

(湖南省常德市第一中学 415000)

一、紧扣教材，牢固正确理解概念

1.在摆角很小(摆角应小于或等于5°)的情况下，单摆所受的回复力与偏离平衡位置的位移成正比而方向相反，单摆做简谐运动.

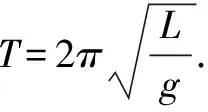
二、紧扣单摆周期公式，应用其便捷解题

单摆在实际中有很多应用，惠更斯利用单摆的等时性发明了带摆的计时器，单摆的周期可以通过改变摆长来调节，计时很方便.单摆的周期和摆长容易用实验准确的测定出来，所以可利用单摆准确的测定出各地的重力加速度.

1．单摆周期公式的一般应用

(1)直接应用单摆周期公式解题

例1 已知单摆a完成10次全振动的时间内，单摆b完成6次全振动，两摆长之差为1.6米，求两单摆摆长La与Lb分别为多少?

解设两个单摆的周期分别为Ta和Tb，由题意10Ta= 6Tb，得Ta∶Tb=6∶10

又因为La-Lb=1.6 m,得：La=0.9 mLb=2.5 m

(2)单摆周期公式与万有引力定律的综合应用解题

例2 有人利用安装在气球载人舱内的单摆来确定气球的高度.已知该单摆在海平面处的周期是T0，当气球停在某一高度时，测得该单摆周期为T，求该气球此时离海平面的高度h.(把地球看作质量分布均匀的半径为R的球体)

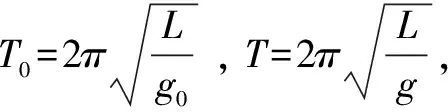
2．单摆周期公式在带摆计时器中的应用

(1)摆钟计时的原理以及快钟、慢钟、标准钟的含义

a、具有任何机械结构的摆钟，都是由钟摆驱动与之相连的齿轮，再通过一系列传动装置使指针走动，从而给出示数的，经历的时间为振动次数n乘以钟摆的振动周期T.

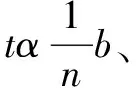
注：无论快钟、慢钟、或标准钟，钟摆每完成一次全振动，钟面秒针指示的时间是相同的，在相同的一段时间内，快钟、慢钟、或标准钟的振动次数则不同.

(2)摆钟计时以及快钟、慢钟的调节

例3 一物体在某行星受到万有引力是它在地球表面受到万有引力的4倍，在地球上标准的摆钟，搬到此行星表面上后，此钟的分针走一圈所经历的时间实际为多少？

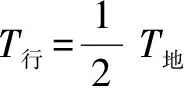
又因为无论在行星还是地球表面摆钟的分针都是走一圈，钟摆的振动次数相同在行星表面分针走一圈所经历的时间实际为0.5 h.

例4 有一座摆钟，它的摆长L=24.96厘米，发现它每昼夜慢5分钟，怎样调节它才走时准确？

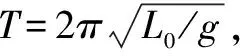
3．利用单摆周期公式测定重力加速度

(2)重力加速度的测定

a.公式法求解

例5 某同学在用单摆法测重力加速度的实验中用游标卡尺测出摆球直径为2.00厘米，让刻度侧尺的零点对准摆线的悬点，摆线竖直下垂，一直测到摆线与摆球的系点，测出摆线的长度87.40厘米，用停表测定了40次全振动的时间为75.2秒，实验地的重力加速度g为多大？

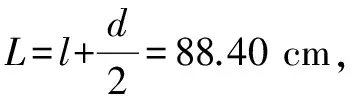
例6 某同学在用单摆法测重力加速度的实验中，所用摆球密度不均匀，无法确定质心，他第一次测得悬线长l1，周期为T1；第二次测得悬线长为l2，周期为T2，根据上

述数据，实验当地的重力加速度g为多大？

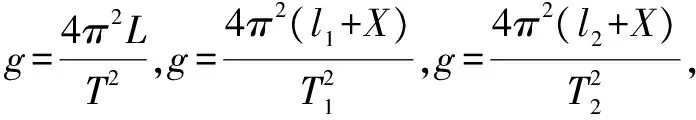
b.图象法求解

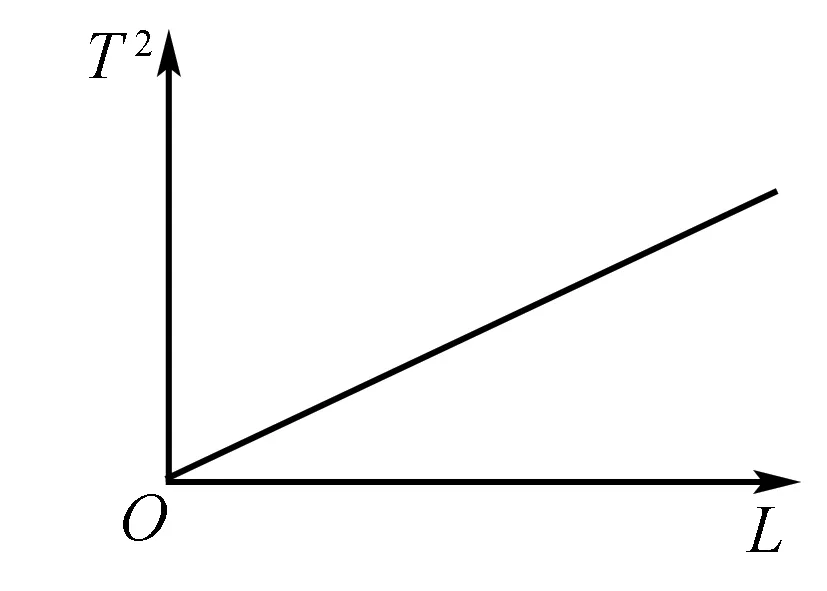
例7 某同学在用单摆法测重力加速度的实验中，多次改变摆长L并测出了相应的振动周期T，从而得出一组相对应的L与T的数据，再以L为横坐标，T2为纵坐标将所得数据描在坐标上，连接所描的点作出T2—L图线是一条过原点的直线，并求出了直线的斜率为k.则实验当地的重力加速度g为多大？

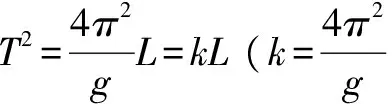
[1] 普通高中课程标准实验教科书.课程教材研究所[M]. 北京：人民教育出版社，2010(04)：55-58.

[2] 宋舒白，杨爱珍.加练半小时[M]. 哈尔滨：黑龙江教育出版社，2014(04)：33-36.