基于GM(1,1)模型的哈尔滨房价走势前瞻

孙 波，罗志坤

(1.哈尔滨商业大学 经济学院 哈尔滨150028；2.哈尔滨商业大学 基础科学学院，哈尔滨150028)

基于GM(1,1)模型的哈尔滨房价走势前瞻

孙 波1，罗志坤2

(1.哈尔滨商业大学 经济学院 哈尔滨150028；2.哈尔滨商业大学 基础科学学院，哈尔滨150028)

以哈尔滨市2015年1月-2016年7月的房价月度数据为背景构造了房价波动的GM(1,1)模型，进而对哈尔滨市未来一段时期的房价变化走势进行了短期统计预测。预测结果表明，自2016年8月～2017年7月，哈尔滨房价整体呈微弱走低态势，但总体看价格变化相对稳定。精度检验结果表明，模型预测效果较好，对房价走势的预测有可信性，预测方法有可行性。

GM(1,1)模型；房价；预测；精度检验

一、引言

住房货币化改革以来，国内一些地区和城市房价的过快上涨直至居高不降引发了一系列社会问题和经济隐忧。仅从2016年的房地产市场看，多地房价的上涨幅度已经远远超过预期，并由此引来管理方持续强化的楼市调控。特别是一线城市和热点二线城市，从2016年10月份开始就推出了系列调控措施，2016年11月份的调控范围又继续扩大，调控力度也空前加强。在这些调控政策的巨大压力下，不少地方的楼市从2016年11月份开始已有所退烧，但一些热点城市依旧处于持续上涨状态，如天津市2016年11月份的房价环比涨幅超过10%，楼市疯狂可见一斑。而且众所周知，房价与普通大众的生活和民生问题息息相关，各地方政府如不能对房价进行有效调控，房价照此势头无止境地被推高，首先普通百姓的居住权就会受到严重影响，进而引发社会问题。加强对房价走势的科学预测和监测是政府有效管控房价、使稳定房价的调控政策有据可依、政策具体实施有的放矢的重要环节。

对未来房价进行科学预测是一项较为复杂的工作。实际上，影响房价的因素很多，例如人均可支配收入、GDP、人口数量、储蓄存款、消费者需求、房地产总投资、银行利率、供需关系、预期价格、地价等等。预测房价的方法也有多种，包括灰色系统理论、神经网络模型，拟合预测模型、ARMA预测模型等。通过技术手段前瞻房价变化趋势是房地产市场研究和调控房价政策设计的重要内容及基本依据。已有研究中预测房价的主要文献有：张兵(2009)[1]基于灰色系统理论分析模型测算了影响安徽省淮南市房地产市场需求的各因素相对重要性；李红波等(李红波、刘滢鸿、徐宁，2012)[2]依据BP神经网络模型由供需相关指标的不确定性波动导致的房价变动分析并预测了房价走势；黄柳铃(2014)[3]基于曲线拟合预测了2011年后北京房价的趋势，强调了国家推出“国十条”的必要性；贺立(2014)[4]在ARIMA模型分析基础上对北京市住房价格进行了中长期预测；李肖萌(2016)[5]建立了PSR模型，对山东青岛房地产调控政策体系进行了深入分析和评价；赵美平、刘永红(2014)[6]基于VAR模型及脉冲响应函数分析了房价收入比和租金比指标的影响；梁浩、杨光宇(2013)[7]利用线性与非线性回归等统计方法对武汉市商品住宅价格的变化趋势做了预测。

考虑到搜集的样本数据和模型特点，本研究将采用灰色系统理论的GM(1,1)模型对哈尔滨未来房价走势进行预测和分析。

二、GM(1,1)模型适用背景

现有经济预测的文献多以时间序列分析为基本方法。这种预测方法是以所能反映的社会经济现象发展过程和规律性进行引伸外推，进而预测其发展趋势。其不足之处在于：

1.当时间序列变化趋势不太明显时，将很难建立起比较精确的预测模型。

2.该预测方法仅在系统按原来趋势发展变化的假设下进行外推预测，而没有充分考虑对未来变化产生影响的各种不确定因素。

考虑到以上不足，将灰色系统[8](Grey System)理论和方法纳入视野是个不错选择。该方法由华中科技大学控制科学与工程教授于1982年提出，是对在一定范围内变化的与时间序列有关的过程进行预测，主要特点是模型使用的不是原始数据序列，而是生成数据序列。如今灰色系统分析法得到快速发展，并不断渗透到自然、社会科学的许多领域。灰色模型(GM)为核心的模型体系是以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系，目前使用最广泛的灰色模型是GM(1,1)模型。

GM(1,1)模型是灰色系统理论的主要内容之一，该模型是一种较为常见的数列预测模型。具体来说，GM(1,1)模型是一阶微分方程，并且只含1个变量。该模型是基于随机的原始时间序列，按时间累加后所形成的新时间序列呈现的规律用一阶线性微分方程的解来逼近。

作为一种中短期预测模型[9]，GM(1,1)模型已广泛应用于社会、经济、生态、工程预测等领域[10-13]。因适应贫信息、抗噪声能力强等特性，该模型显示出比传统预测方法更大的优越性。在对经济变量进行定量预测时，若没有大的市场波动与政策冲击，其预测结果一般较为可信。由于不同经济问题在建模过程中遇到的实际情形不同，若存在对预测对象影响较大的因素，就要在定性分析层面上追踪原始数据信息突变点的具体对应事件或原因，然后再对预测值作必要修正，使之更接近于实际情况，提高预测值的可信度，为科学决策提供技术支持。

此外，GM(1,1)模型适用于具有较强指数规律的序列，只能描述单调的变化过程。对于非单调的摆动发展序列或有饱和的形序列，可以考虑使用GM(2,1)模型、DGM和Verhulst模型[14]。具体来说，GM(1,1)模型的适用范围如下：

不难证明[8]，当GM(1,1)模型的发展系数|α|<2时，GM(1,1)模型是有意义的；否则，当|α|≥2时，GM(1,1)模型将不再有意义，换句话说，GM(1,1)发展系数α的禁区为区间(-∞,-2]∪[2,+∞)。在此区间内，GM(1,1)模型失去意义。随着发展系数的不同取值，预测效果也不尽相同。有如下结论：

(1)当-α≤0.3时，GM(1,1)模型1步预测精度在98%以上，2-5步预测精度在97%以上，适用于作中长期预测；

(2)当0.3≤-α≤0.5时，GM(1,1)模型1～2步预测精度都在90%以上，10步预测精度也高于80%，适用于作短期预测，作中长期预测要慎用；

(3)当0.5<-α≤0.8时，GM(1,1)模型不适宜作短期预测；

(4)当0.8<-α<1时，GM(1,1)模型1步预测精度将低于70%，应采用残差修正模型；

(5)当-α>1时，GM(1,1)模型不再适用。

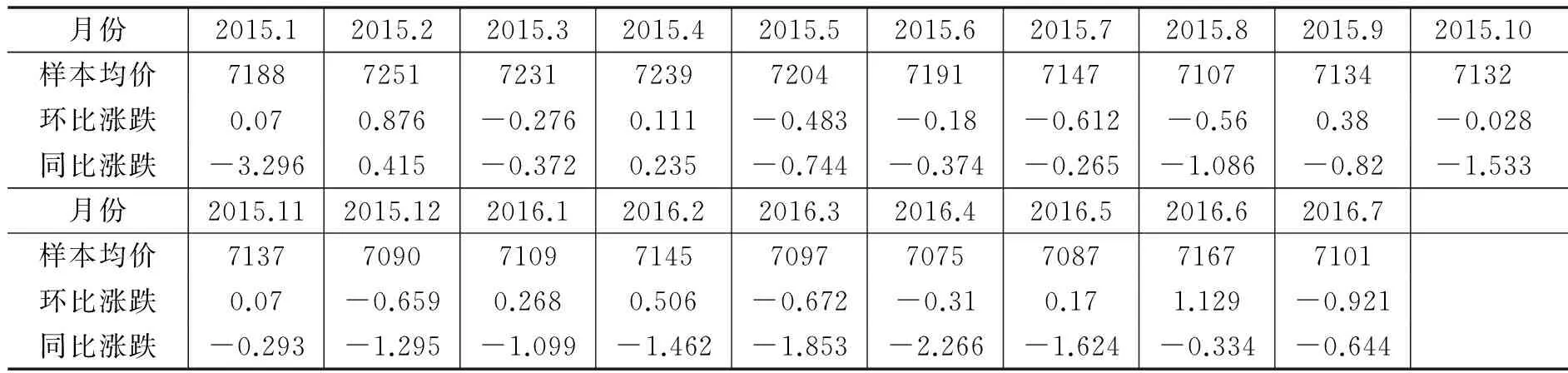
表1 2015年1月-2016年7月哈尔滨新建住宅均价

数据来源：中国指数研究院—中国房地产指数系统百城价格指数报告

三、哈尔滨房价未来走势实证分析

本部分我们将采用GM(1,1)模型，根据哈尔滨2015年1月至2016年7月的新建住宅均价序列(见表1)，对哈尔滨未来一年的房价走势变化进行预测。

具体建模方法与步骤如下[14]：

1.数据的检验与处理

为了确保建模方法的可行性，需要对已有数据作必要的检验处理。

根据表1可建立哈尔滨房价数据时间序列：

x(0)=(x(0)(1),x(0)(2),L,x(0)(19))=(7188,7251,7231,7239,7204,7191,7147,7107,7134,7132,7137,7090,7109,7145,7097,7075,7087,7167,7101)

首先，计算序列的级比λ(k)，有：

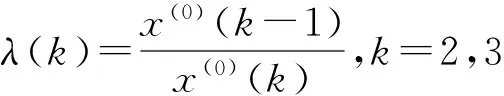
λ=(λ(2),λ(3),L,λ(19))=(0.9913,1.0028,0.9989,1.0049,1.0018,1.0062,1.0056,0.9962,1.0003,0.9993,1.0066,0.9973,0.9950,1.0068,1.0031,0.9983,0.9888,1.0093)

其次，进行级比判断。由于所有的λ(k)=[0.9048,1.0999],k=2,L,19，故序列x(0)可以作为GM(1,1)模型的数据进行灰色预测。

2.GM(1,1)建模

(1)对原始数据x(0)作一次累加生成序列(1-AGO)，进而消除原始数据的随机性与波动性，从而有：

x(1)=(x(1),x(1)(2),L,x(1)(19))=(x(0)(1),x(0)(1)+x(0)(2),L,x(0)(1)+x(0)(2)+L+x(0)(19))=(7188,14439,21670,28909,36113,43304,50451,57558,64692,

71824,78961,86051,93160,100305,107402,114477,121564,128731,135832)

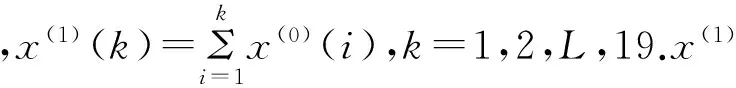
z(1)=(z(1)(2),z(1)(3),L,z(1)(19))=(10813.5,18054.5,25289.5,32511,39708.5,46877.5,54..4.5,61125,68258,75392,82506,89605.96732.5,103853.5,110939.5,118020.5,125147.5,132281.5)

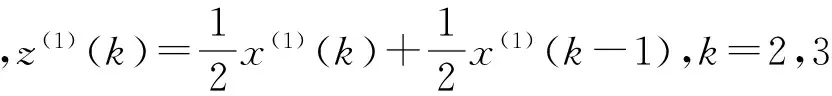
(2)建立灰微分方程:

x(0)(k)+αz(1)(k)=b，k=2,3,...,19

相应的白化方程为：

(1)

构造数据矩阵B及数据向量Y，有

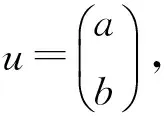
则由最小二乘法，求得使J(u)=(Y-Bu)T(Y-Bu)达到最小值u的估计值为:

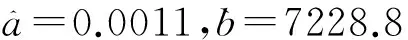
于是求解方程 (1)得：

(2)

3.检验预测值

为确保所建GM(1,1)模型有较高的精度能应用于实际问题，按灰色理论一般要通过以下几个指标如，相对误差、平均相对误差、关联度、小误差概率等对模型的质量进行检验。

ρ为分辨系数，因分辨系数ρ是在(0，1)中取定的实数，一般取ρ=0.5。在此情况下，通常认为关联度大于0.6时能够接受，也就是说关联度检验合格，否则关联度就比较差。关联度的计算公式如下：

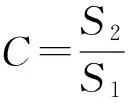
(5) 小误差概率。

利用Matlab软件编程并求解模型的各种检验指标值：

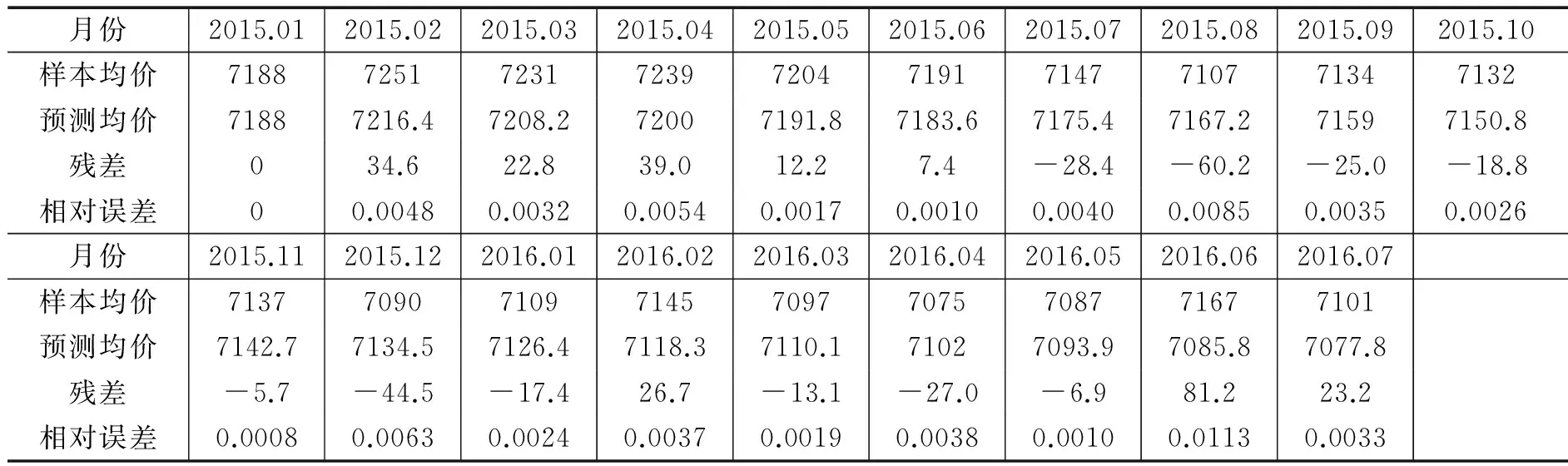
表2 预测均价

GM(1,1)精度检验对照表为：

表3 精度检验对照表

对照表3可以看出：平均误差等级为一级，关联度等级约为四级，均方差比值约为二级，小误差概率约为一级，所以整体看模型运行结果是可信的。

用Matlab软件画出样本均价及预测均价随月份变化如图1所示：

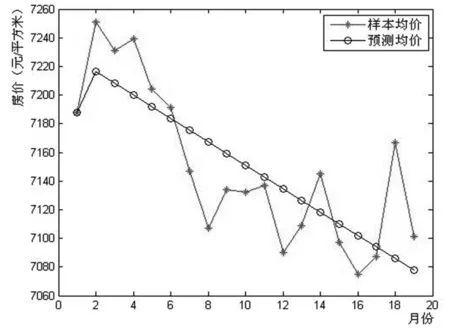
图1 样本均价与预测均价比较

从图1可以看出预测均价与样本均价弥合较好。

4.房价变化趋势预测

经过验证，本文所建构的GM(1,1)模型精度较高，完全可用于房价预测。基于该模型，我们进一步预测未来一年内哈尔滨的房价变化趋势，结果如表4。

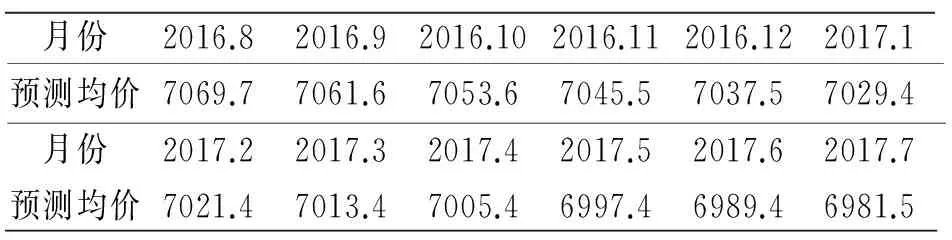
表4 2016年8月-2017年7月哈尔滨房价预测值

预测结果显示，未来一年内哈尔滨房价将呈现小幅下降，但总体而言波动不大，走势相对稳定。

5.GM(1,1)模型算法的改进与展望

灰色系统理论提出的时间并不长，其理论体系尚不十分完善，仍然存在一些急需研究与改进的问题。虽然GM(1,1)模型具有广阔的应用领域，但是该模型也有一定的适用条件[15]。GM(1,1)模型基于最小二乘法的指数拟合曲线，不可避免会产生一些偏差，当进行长期预测时效果不明显，缺乏预期的稳定性。可从以下几个方面考虑加以改进：

(1)改进模型初值，进行合理选取[16]；

(2)利用多项式拟合估计参数和求解值优化的改进[17]；

(3)基于灰色预测代数递推方程，以此代替原来灰色预测的微分方程或白化方程[18]；

(4)采用线性多步法中的四阶Adams显式及隐式公式优化GM(1,1)模型，从而提高模型模拟效果和预测精度[19]。

GM(1,1)模型建模方法比较简单，Matlab实现容易，具有较强时效性与实时性，即使对少量数据贫信息的情形同样可以进行计算和预测，预测精度非常高，适应性也很强，通过对原始数据的前期处理，达到弱化数据波动性的目的，使灰色数据逐渐变白，呈现出一定的规律性。当然，GM(1,1)模型精度和预测精度受数据数列的光滑度影响较大，当数据样本不是很多时，模型精度和预测精度受个别特别突变的数据影响较大。另外，模型只是关注了数据内在的发展规律，并未考虑到外界环境(如政策、气候等因素)。

由于本文运用GM(1,1)模型对房价进行预测，而房价预测与人口预测、汇率预测有很多相似的特点，所以该模型可以推广到人口预测和汇率预测等。

四、结论

房价问题一直都是我国政府和社会各界最为关注的热点问题之一。在技术上实现对房价水平和变化情况的准确、及时、真实传递，是开展相关分析、研究和制定具体管理调控政策的基准依据。本文基于哈尔滨房价历史数据构建了房价波动的GM(1,1)模型，并对哈尔滨房价变化进行了短期统计预测。预测结果表明：未来一年内，哈尔滨的房价总体上维持相对稳定态势，有微小降幅。只要市场预期未受到根本逆转，哈尔滨的房价将在合理范围内波动，不须人为政策干预。

[1] 张 兵. 基于灰色理论的房地产需求分析——以安徽淮南市房地产市场为例[J]. 区域金融研究, 2009，(6): 66-68.

[2] 李红波, 刘滢鸿, 徐 宁. 基于BP神经网络模型的房价敏感性分析[J]. 昆明：昆明理工大学学报：社科版, 2012, 12(6): 57-63.

[3] 黄柳铃. 基于曲线拟合的房价调控模型的建立[J]. 宁德师范学院学报: 自然科学版, 2014, 26(4): 374-375.

[4] 贺 立. 基于时间序列分析的2014年北京商品住宅价格指数预测[J]. 东方企业文化, 2014，(3)：305.

[5] 李肖萌. 基于PSR模型的青岛市房地产调控政策评价体系分析及建议[J]. 中国市场, 2016，(17):122-123.

[6] 赵美平, 刘永红. 基于VAR模型的中国房价收入比、房价租金比与房价关系的研究[J]. 科技视界, 2014，(23):270.

[7] 梁 浩, 杨光宇. 基于回归分析和傅里叶级数分析的房价模型[J]. 现代商贸工业, 2013，(16):105-106.

[8] 邓聚龙. 灰色预测与决策[M]. 武汉：华中理工大学出版社, 1986.

[9] 黎精明, 刘方圆, 李鹏辉. 基于等维动态GM(1,1)均值模型的CPI预测[J]. 统计与决策, 2016，(13)：30-33.

[10] 曲江文, 刘建平, 杜建伟,等. GM(1,1)灰色模型在疟疾疫情预测中的应用[J]. 医学与社会, 2006, 19(11): 5-7.

[11] 宋秀英. 基于MATLAB的灰色预测GM(1,1)模型在经济分析中的应用[J]. 数学学习与研究, 2011，(11): 93-95.

[12]周 刚, 王弘宇, 胡春雪，等. 应用灰色新陈代谢GM(1,1)模型预测中长期城市需水量[J]. 中国农村水利水电, 2005，(8): 16-18.

[13]周 健, 刘占才. 基于GM(1,1)预测模型的兰州市生态安全预警与调控研究[J]. 干旱区资源与环境, 2011, 25(1):15-19.

[14]司守奎, 孙玺菁. 数学建模算法与应用[M]. 北京：国防工业出版社, 2011.

[15]刘思峰, 邓聚龙. GM(1,1)模型的适用范围[C] 全国青年管理科学与系统科学论文集(第5卷). 1999:121-124.

[16]岳 希, 杨 洋. 基于最小误差化的GM(1,1)模型的优化及应用[J]. 计算机应用研究, 2016, 33(8):2328-2330.

[17]李梦婉, 沙秀艳. 基于GM(1,1)灰色预测模型的改进与应用[J]. 计算机工程与应用, 2016, 52(4):24-30.

[18]张锦秀, 徐丙振. GM(1,1)灰色预测方法的改进[J]. 统计与决策, 2016，(11):16-18.

[19]沈 艳, 张丽玲, 刘 垠,等. 基于线性多步法的GM(1,1)模型优化及应用[J]. 数学的实践与认识, 2016，(17):182-188.

[责任编辑：姜 野]

Foresight Analysis to Housing Price of Harbin Based on GM (1, 1) Model

SUN Bo1，LUO Zhi-kun2

(1.School of Economics， Harbin University of Commerce，Harbin 150028,China；2.School of Basic Science，Harbin Univesity of Commerce,Harbin 150028,China)

On the monthly data of housing price of Harbin city from January 2015 to July 2016, we construct GM (1, 1) model of housing price fluctuation for short-term forecasting to the future housing price change in Harbin. Prediction results show that the housing price in Harbin descends weakly on the whole from August 2016 to July 2017，but the housing price changes is relatively stable in general. Accuracy test reveals that the forecasting effect of this model is fine，credible,feasible as well.

GM (1, 1) model；housing price; prediction; accuracy test

2016-11-10

教育部人文社会科学研究规划基金项目(13YJA790100)；黑龙江省哲学社会科学研究规划项目(12D086)

孙 波(1971-)，男，黑龙江呼兰人，教授，博士生导师，研究方向为宏观经济理论与政策；罗志坤(1984-)，男，黑龙江哈尔滨人，讲师，理学博士，研究方向为数理经济分析与建模。

F293.35;F714.1

A

1671-7112(2017)01-0108-06