矩阵乘积关于广义逆的交换律与混合交换律

刘林林 缪迎迎 李 莹

(聊城大学 数学科学学院,山东 聊城 252059)

0 引言

矩阵的各种类型的广义逆在实际的生活中都有广泛的应用.它们在概率统计、数学规划、控制论、测量学、博弈论和网络理论等领域有极其重要的作用[1,2],而且在一些统计问题如长方及病态线性方程问题、最小二乘问题及马尔可夫链等中也是一种基本的工具.就是因为广义逆应用的广泛性,所以要求其自身的理论发展不断地充实完善.

我们知道,若A∈Cn×n非奇异,则一定存在AA-1=A-1A.可是对于A的{i,j,k}-逆,不一定存在A(i,j,k)∈A{i,j,k}使AA(i,j,k)=A(i,j,k)A.因为在有些情况下,交换律成立可使得问题得以简化,所以我们有必要研究{i,j,k}-逆的交换律成立的条件.本文运用矩阵秩方法和SVD(singular value decomposition)[3],研究了矩阵乘积关于{1,2,3}-逆与{1,3,4}-逆的交换律以及混合交换律成立的充分必要条件.

1 预备知识

令Cm×n表示所有m×n阶复矩阵的集合.对于一个给定的矩阵A∈Cm×n,A的共轭转置、秩与值域分别用A*、r(A)和R(A)表示,In表示n阶单位矩阵.矩阵A∈Cm×n的Moore-Penrose逆A+为满足下列四个等式的唯一矩阵G∈Cm×n

(1)AGA=A;(2)GAG=G;(3) (AG)*=AG;(4) (GA)*=GA,

令φ≠η={i,j,k}⊆{1,2,3,4},用Aη表示满足以上四个方程中的(i),(j),(k)的矩阵X的集合,Aη中的任何一个矩阵G称为矩阵A的一个{i,j,k}-逆(或η-逆),记为A(i,j,k).A*,A的零空间上的正交投影分别用EA=I-AA+,FA=I-A+A表示.

定义1[4]设A∈Cn×n,φ≠η,ξ⊆{1,2,3,4}.对于X∈Aη,Y∈Aξ,如果AX=YA,则称矩阵乘积关于X与Y满足交换律.

引理1[5]设A∈Cm×n,B∈Cm×k,C∈Cl×n.则

引理2[5]设A∈Cm×n,B∈Cm×k,C∈Cl×k,D∈Cl×k.则

(1)

设A,B1,B2,C1,C2及X1,X2使得矩阵表达式A-B1X1C1-B2X2C2有意义.则

(2)

其中

设A,B,C,D,P及Q使得D-CP+AQ+B有意义.则

(3)

引理3[6]设A∈Cm×n,B∈Cm×k,C∈Cl×k.则

(4)

(5)

引理4[7]设A∈Cm×n,B∈Cm×k,C∈Cl×n.若R(AQ)=R(A),R((PA)*)=R(A*).则

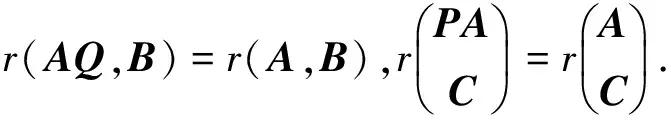
特别地,

2 矩阵乘积关于{1,2,3}-逆和{1,3,4}-逆的交换律

定理1 设A∈Cn×n, 则以下两个条件等价:

(1) 存在A(1,2,3)∈A{1,2,3},使得A(1,2,3)A=AA(1,2,3)=AA+成立;

利用(1)和(4)得

利用引理4, 通过化简计算, 得到

因此,

定理2 设A∈Cn×n,则以下四个条件等价

(1) 存在A(1,3,4)∈A{1,3,4},使得A(1,3,4)A=AA(1,3,4);

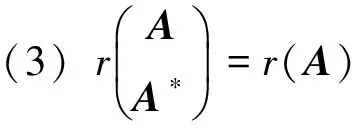
(4)R(A*)=R(A).

其中,X4为适当阶数的任意矩阵.

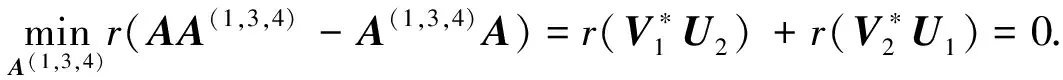
利用(1)和(3)

同样地, 我们有

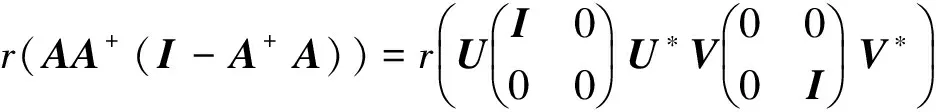
已知r(A*A)≤r(A),又A=(A+)*A*A,得r(A)≤r(A*A),故r(A*A)=r(A).

因此,

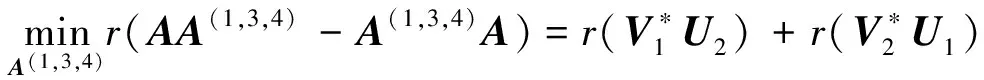
3 矩阵乘积关于{1,2,3}-逆与{1,3,4}-逆的混合交换律

定理3 设A∈Cn×n, 以下四个等价条件成立:

(1) 存在A(1,2,3)∈A{1,2,3},A(1,3,4)∈A{1,3,4},使A(1,3,4)A=AA(1,2,3);

(4)R(A*)=R(A).

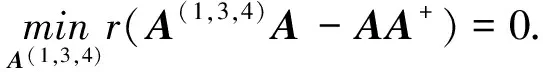
由(1)及(5)得,

利用引理4, 通过化简计算, 得到

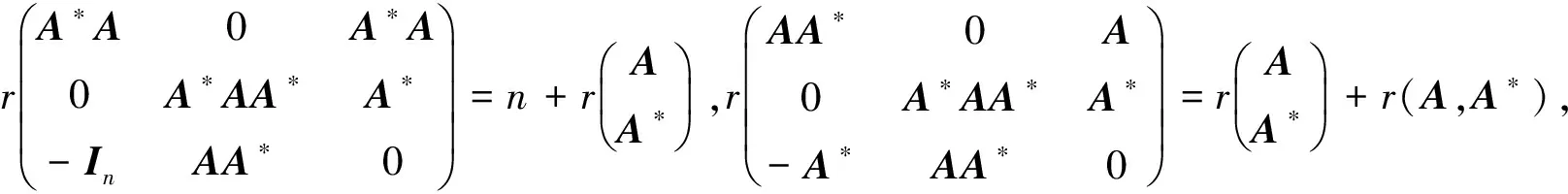
因此,

定理4 设A∈Cm×n,则以下两个条件等价:

(1) 存在A(1,2,3)∈A{1,2,3},A(1,3,4)∈A{1,3,4},使A(1,2,3)A=AA(1,3,4);

(2)r(A,A*)=r(A2).

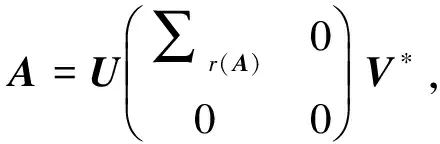
其中,X3,X4为适当阶数的任意矩阵.

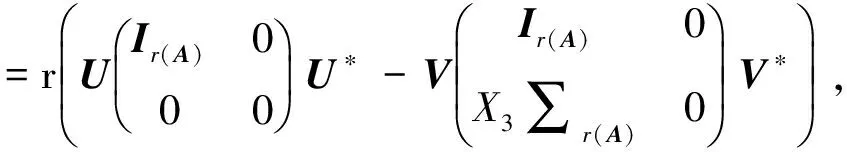
利用(2)可得

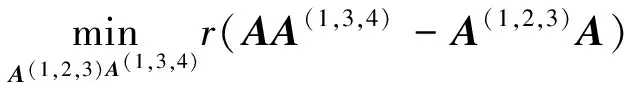
其中

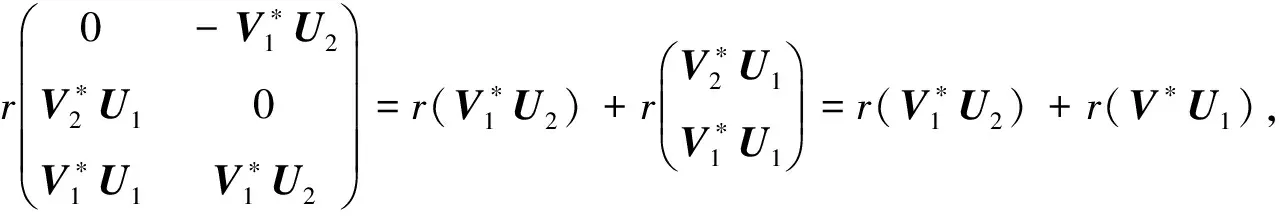
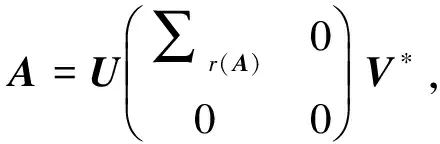
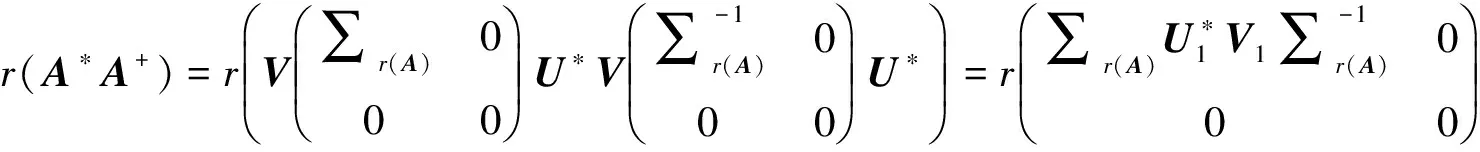
利用(1)

所以,

故结论成立.

4 结束语

本文对两个矩阵乘积关于{1,2,3}-逆与{1,3,4}-逆的交换律与混合交换律进行了讨论，得到了矩阵乘积关于{1,2,3}-逆与{1,3,4}-逆交换律成立的充要条件.我们也可采用同样的方法讨论其他类型的广义逆的交换律.

[1] 王松桂,杨振海. 广义逆矩阵及其应用[M].北京:北京工业大学出版社,1996.

[2] 郭文彬,魏木生. 奇异值分解及其在广义逆理论中的应用[M].北京:科学出版社,2008.

[3] 郭文彬,周尚启,张丽梅. 奇异值分解中非奇异矩阵的性质结构[J].聊城大学学报:自然科学版,2005(1):11-15.

[4] 赵晓宇.矩阵乘积关于{1,i}-逆与{1,j}-逆的混合交换律[J]. 聊城大学学报:自然科学版,2010, 12: 42-48.

[5] MarsagliaG,Styan G P H.Equalities and inequalities for ranks of matrices[J]. Linear and multilinear Algebra, 1974. (2):269-292．

[6] Tian Yongge. More on maximal and minimal ranks of Schur complements with applications[J]. Appl Math Comput,2004, 152:675-692.

[7] Hu D. The general solution to the matrix equation AXB+CYD=E[J]. Math Practice Theory, 1992, 4: 85-87.

[8] 李莹, 高岩, 郭文斌. 矩阵乘积关于广义逆的交换律及广义交换律[J]. 上海理工大学学报,2011,4：379-383.

[9] Ben-Israel A. Generalized inverses theory and applications[M]. New York：John Wiley & Sons, 1974.