对话引导探索 过程彰显主体——以“勾股定理的逆定理”的教学为例

陈 锋（江苏省无锡市太湖格致中学）

张杭嫣（江苏省无锡市水秀中学）

对话引导探索 过程彰显主体
——以“勾股定理的逆定理”的教学为例

陈 锋（江苏省无锡市太湖格致中学）

张杭嫣（江苏省无锡市水秀中学）

数学课堂注重引导学生充分经历观察、实验、猜测、计算、推理、验证等探究过程；注重师生自然地对话与互动，促使学生的思维得以层层展开与深入，进而积累基本的数学活动经验，感悟重要的数学思想，发展终身学习的数学观念.结合“勾股定理的逆定理”一节的课堂教学进行深入地探究和思考，以期对教师教学有所帮助.

对话引导；探索研究；数学思想

一、教学背景

勾股定理，是数学史上一颗最璀璨的明珠，无论是中国人引以为傲的“勾三股四弦五”，还是闻名世界的“毕达哥拉斯定理”，都是数学史中最珍贵的瑰宝．在一次市级的赛课比赛中，当笔者知道拿到的比赛课题为苏科版《义务教育教科书·数学》八年级上册第三章第二节“勾股定理的逆定理”后，一种失望和懊恼的情绪油然而生，为什么不是“勾股定理”呢？然而，通过认真研读教材、精心设计课堂及反复地思考斟酌之后，笔者才发现，勾股定理的逆定理也是一颗闪耀着光芒的珍珠.在内容上，勾股定理的逆定理是学生在掌握勾股定理的相关结论后，从逆命题的角度对三角形的三边关系与三角形的形状之间的联系做进一步探究，通过正、逆两个角度的互相转化，学生能进一步加深对勾股定理的理解与认识．在思想方法上，引导学生通过画图、观察、猜想去经历探索勾股定理逆定理的过程，积累基本的数学活动经验，发展终身学习的数学观念．此外，感受用构造法证明勾股定理逆定理的过程，体会在数学中发现、类比、化归的思想，也渗透着猜想、试验、探索、归纳等重要的数学方法．下面，笔者就以赛课过程中的一个片断摘录及赛课后的教学思考来具体谈谈本节课所带来的思考与感悟．

二、教学目标、重点、难点阐述

教学目标：（1）充分经历观察、实验、猜测、计算、推理、验证等勾股定理的逆定理的得出活动过程，掌握勾股定理的逆定理.

（2）理解命题、逆命题、逆定理的概念及关系.

（3）感悟构造法、数形结合等重要的数学思想，树立大胆猜想，勇于探索的创新精神.

教学重点：经历勾股定理逆定理的得出过程，掌握勾股定理的逆定理.

教学难点：用对话引导采用构造法突破辅助线.

三、教学片断摘录

1.命题引入，感受互逆

师生共同复习勾股定理，即直角三角形中两直角边的平方和等于斜边的平方．

师：你能说出勾股定理的逆命题吗？

师生共同整理出勾股定理的逆命题，即如果一个三角形中两条较短边的平方和等于最长边的平方，那么这个三角形是直角三角形．

师：你觉得这个逆命题正确吗？

学生一时无法确定．

【设计意图】学习完勾股定理，从数学本身的特质出发，自然引发新的学习内容，即勾股定理的逆命题．这样开门见山的做法，既让学生快速接触主题，同时又理清了本节课与前一节课——勾股定理之间的关系，为后续的几何学习提供学习方法的指导．

2.引导操作，感知结论

从埃及人的绳结问题入手，初步感知结论的正确性．

师：今天我们将沿着古人的足迹，继续我们的探索之路，古人用了绳子这一生活实物探索，今天的数学课堂上我们将借助于直尺、圆规等数学工具开展深入探究．

试验探究：

（1）6，8，10和5，12，13这两组数满足勾股定理的逆命题所需要的条件吗？

（2）分别以6 cm，8 cm，10 cm和5 cm，12 cm，13 cm为三边画两个三角形，它们是直角三角形吗？

【设计意图】在学生一时无法判断的基础上教师适时用古埃及人画直角的方法引导学生猜想——三角形三边满足什么条件下可以判定一个三角形是直角三角形？为学生的探究提供了尝试的入手点，让学生沿着古人的足迹，从画图开始，通过两组具体数据的实际操作，初步感知直观结论，即如果△ABC的三边满足a2＋b2＝c2，那么这个三角形是直角三角形．

3.严格证明，总结定理

师：要判断一个命题是正确的，只靠两个实例能否确认？

生：不能，要判断一个命题是正确的必须经过严格的证明．

师：太棒了，让我们一起开始证明之旅．

师：已知：如图1，在△ABC中，AC2+BC2=AB2，求证：∠C=90°．

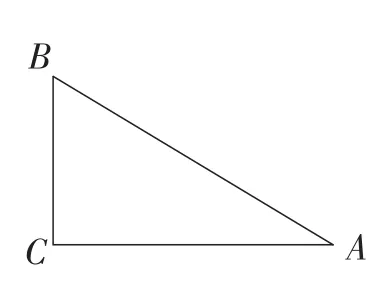
图1

图2

学生陷入沉默，无法入手．

师：拿到一个几何证明题，我们一般是从哪里入手？

生1：从已知条件入手．

师：从已知的AC2+BC2=AB2，你能想到什么呢？

生2：想到勾股定理．若△ABC是直角三角形，可以得到AC2+BC2=AB2．

师：那现在已知条件中的△ABC是直角三角形吗？

生3：不是，是要我们证明它是直角三角形．

师：那就是说为了要用已知条件，我们最好有一个直角三角形，而这个直角恰好又是求证中的结论，已知和求证都指向了同一个集中点，你看出是什么了吗？

生3：要有直角．

师：对了，要有一个直角，题目中有吗？

生3：没有．

师:那怎么办呢?

生3：画一个就好了．

师：好，听你的．作∠D=90°，直角有了，接下来做什么？

生4：想办法使用已知条件AC2+BC2=AB2．

师：怎么使用呢？

生4：用圆规截取．（生4上黑板板演操作）如图2，过点D截取DE=AC，DF=BC，EF=AB．

生5：不对，截取完DE=AC，DF=BC之后EF就已经产生了，不用再截取了,只需要连接EF就可以．

师：好极了！现在出现在我们眼前的图形让你想到了什么？

生6：想到全等三角形．

师：说出证明全等需要的条件．

生6：DE=AC，DF=BC．

师：够了吗？

生6：还有EF=AB．

师：你怎么得到EF=AB的呢？

生6：因为AC2+BC2=AB2，DE2+DF2=EF2，且DE=AC，DF=BC，

所以EF=AB．

所以△ABC≌△EFD.

所以∠C=∠D=90°．

师：好，我们终于通过自己的努力证明了这个命题是正确的，因此它也可以成为一条定理，由于它和勾股定理之间的特殊关系，我们称它为勾股定理的逆定理．

【设计意图】在大胆猜想的基础上进一步提出小心求证的要求，引导学生尝试用严密的几何推理证明结论．在此过程中，当学生陷入沉默时，教师用和谐的对话引导学生轻松突破构造法这一思维难点；当学生找到灵感时，教师适当把舞台留给学生，让他们尽情地用尺规作图一步步逼近终极目标；当学生出现错误时，让急于表达的其他学生来纠正错误，为正确的证明保驾护航，最终到达胜利的彼岸，最后通过对比勾股定理，顺利总结出勾股定理的逆定理．

四、教学思考

1.抓住数学本质思考，注重方法总结指导

在新课的引入过程中，笔者也曾绞尽脑汁地设计精彩的情境引入，意图最快地抓住学生的眼球，如神秘的古巴比伦泥板图片，雄伟的埃及金字塔图像等，但在其后的思考中总感觉这些情境对学生来说稍显陌生，学生在这些情境中无法快速接近本节课的主题．此时，灵光突然一闪，为什么不通过最直接的数学本质问题入手呢？学完了勾股定理，我们自然应该联想到探究它的逆命题，在前面角平分线、垂直平分线的学习过程中我们不都是这么做的吗，而这也正是几何学习中最常规的学习途径.对于一个几何图形，我们总是要从性质和判定这两个角度来进行研究，可能在直角三角形这一内容时，学生还只是朦胧的感知，而随着学习内容的逐步深入，到等腰三角形，平行四边形，矩形，等等，一次一次的感知后，学生逐步掌握学习的规律与方法，对于一个几何图形，就是要从性质和判定两个方面来研究，此时，学习的方法、体系逐步形成，这不正是我们数学学习最终的目的——“教，是为了不教”吗？从今天扶着学生走，直到有一天尝试放开手，学生照样能昂首阔步继续向前走，而且走得更稳，更快.而要达到这个境界，需要教师在每一节课上抓住数学的本质思考，注重学习方法的指导与整理，让有效的思考成为学习中的一种自然行为，并自觉形成知识体系与方法．

在定理的探究与证明过程中，也应注意渗透方法指导，“大胆猜测—直观验证—小心求证”，这是后续几何学习的一个重要的学习方法，在定理的证明过程中从已知与求证两个角度来分析条件与结论，寻找入手点的方法也可以说是几何证明最经典的方法.而定理证明的“构造法”，也体现了几何辅助线添加的基本原则——因需而生，自然生成．以上种种，都体现了几何学习中最基本的思路与方法，只有从问题的本质出发加深思考，学生才能逐步理解知识体系的“源”，掌握知识运用的“根”，形成知识拓展的“能”，才能在以后的学习中达到以不变应万变的最高境界．

2.自然对话引导探索，注重师生互动学习

《义务教育数学课程标准（2011年版）》（以下简称《标准》）指出，学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程．而本节课的定理探索阶段，正是对这一过程的精彩呈现．

在本节课中，教师以思维为基础的设问必将引发学生的思维探究，通过对话，通过对这种实际问题的解决及这种互动式的解决方式，学生分析问题的能力能够得到很大的发展．今后，在面对陌生问题时他们就不会再束手无策，而会按照平时对话过程中形成的思考方法来尝试分析．对话交流，让学生在倾听与表达中主动参与到问题的探究之中.正是在师生自然的对话与互动中，学生的思维得以层层展开与深入，直至最终揭示教学的内涵；学习的方法逐步走向深入与理性，逐步感知定理证明的基本过程；课堂的气氛从和谐走向精彩，火花频现．从而让学生感受到数学的魅力，体会学习数学的成就感，提高学习数学的兴趣.

3.过程彰显学生主体，注重课堂学生参与

在本节课中，教师自始至终都在努力践行“以生为本”的理念，学生的主体地位得到了充分的体现．自主审题，动手操作，画图验证，对话互动，质疑争论，无不彰显了学生的主体地位，处处闪耀着他们的能力与智慧．在教师的引导下把数学课堂演变为生生、师生的研讨课.课堂上，学生的思维始终处于活跃的思考、交流、争辩状态之中，如此和谐的氛围，有利于让学生说出自己的所有想法．数学课堂中需要暴露学生的思维，而学生思维的深度参与，正是课堂活动的核心标志和最佳体现．本节课体现的是在实践中“做数学”，体现的是活动化的数学观，它重视学生的参与，让学生在做的过程中，体验三角形三边满足什么特殊条件时会形成直角三角形，并通过画图测量、猜想逆命题，直至最终证明完成成为定理．这个设计针对学生的身心特点，调动学生学习的积极性，通过简单的操作活动引起学生直观的猜想，并激发学生探究的欲望．这样的教学，更有利于学生主动地掌握知识和形成能力．有效教学，必须把教师的教落实到学生的学上去．课堂，如果学生不积极参与，最后又通过谁落实学习效果的提升呢？所以，教师的所有教学行为，在最后都反映在学生的学习成果上．当然，学生的学习成果，并不只是看得见的解题能力，更多的还有学习习惯与思维品质的发展与提升，使之成为有效课堂，高效课堂．

4.拉长知识探究过程，注重思想方法渗透

爱因斯坦说，学校教育的成功与否，就在于学生将教材知识遗忘之后，还留下什么样的素质．《标准》也向我们强调，数学教学并非只是为了交给学生书本上的知识，基本的思想与方法就是学生在学习数学的过程中的又一项重要法宝，它依托知识而产生，渗透在知识学习的过程中，同时，思想方法的渗透又能带动具体知识内容的教学，可谓互惠互利．因此，本节课充分展现了定理的提出、形成和发展的过程，拉长了知识探究的过程，注重过程设计，让学生充分经历独立思考、自主探索、合作交流的过程，让他们在活动中逐步积累活动经验、感悟数学思想、形成解题能力．在探索的过程中学生认真体会着在数学中发现、类比、化归、建模等基本思想，也努力感悟着猜想、试验、探索、归纳等重要的数学方法.当这些思想与方法在我们的课堂上慢慢积累，在问题解决的过程中徐徐推进时，我们坚信：量变必然会产生质变！当学生日日“浸润”与“熏陶”在思想与方法的海洋中时，从最初的朦胧状态走向明朗，再到自觉运用，这既是学习的过程，又是经验的积累.在后续学习中，当学生在遇到含有一个未知的数学问题时，他们会遵循平时积累的数学活动基本经验，尝试寻找解题思路，会延续平时数学学习中常用的探索思路，尝试突破未知到已知的关卡．数学的试题可谓千变万化，但万变不离其宗，教师要重视对学生思维习惯的培养，让学生在课堂中注意积累基本的解题思路与方法，那么，他们在遇到综合性较强的练习时，也会回忆课堂相关知识点的作用，寻找突破口，从而达到事半功倍的效果．

当然，数学思想与方法的渗透是一个长期累积的过程，更是一个潜移默化的过程，我们不能指望这一节课能让所有的学生一下子学会所有的重要数学思想与方法，但要坚信：只要我们坚持不懈地努力，遵循逐级递进、螺旋上升的原则，拔节的美丽声音必然会响彻我们的数学课堂.

［1］陈锋，薛莺.以问题引领 提升复习效能：对初三“圆的复习课”的几点感悟［J］.中学数学（初中版），2013（10）：17-19.

［2］陈锋，薛莺，童伟伟.多元化的“微探究”：从机械记忆走向理解建构［J］.中学数学（初中版），2013（18）：76-78.

［3］陈锋，薛莺.从课堂“微探究”谈初中数学有效教学［J］.中学数学教学参考（中旬），2013（4）：16-18.

2016—08—23

陈锋（1977—），男，中学高级教师，主要从事课堂教学研究.