赏·析·解·思·变——说题实践与收获

来林芳（浙江省杭州市浦沿中学）

赏·析·解·思·变
——说题实践与收获

来林芳（浙江省杭州市浦沿中学）

说题是提高教师业务水平的一条有效途径，以“说题案例分析”的形式，从赏题、析题、解题、思题、变题这几方面研究入手，立足于课堂教学的灵活应用，从而有效地培养学生的发散思维、解题习惯，切实提高学生发现问题、分析问题、解决问题的能力，使数学课堂的“轻负高质”得以落到实处.

数学说题；解题能力；教学启示

一、引子：说题引起的思考

2015年10月15日，笔者参加了区中学数学说题比赛.此次说题，从选题之巧、分析之妙、解法之多、变式之活，无一不给笔者留下深刻的印象，给教学带来了深刻的启示.

说题一般包含赏题、析题、解题、思题、变题五个方面.赏题包含说题目的来源与背景、说题目的内涵及功能即所涉及的知识、技能、思想和方法.析题包含分析题目和分析学生两部分.分析题目即分析题目的条件和结论，如何从条件出发一步一步与结论打通或者如何从结论出发一步一步与已知打通；分析学生即分析学生对此题已有的知识与经验、可能会遇到的困难等.解题即此题的解法，一般含一题多解.思题指说题后的反思和对今后教学的一种思考.变题指改变此题的部分条件或结论，探索旧的结论是否成立，或者得出新的类似的结论，或者得出一个全新的结论.

二、说题案例分析

下面以2015年四川省资阳市中考数学第23题为例加以说明.

题目如图1，E，F分别是正方形ABCD的边DC，CB上的点，且DE=CF，以AE为边作正方形AEHG，HE与BC交于点Q，连接DF.

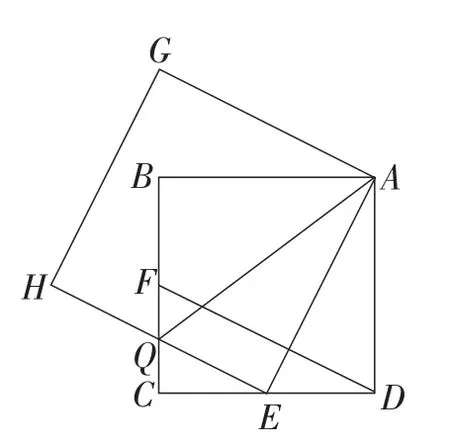
图1

（1）若E是CD的中点.求证：Q为CF的中点；

（2）连接AQ，设S△CEQ= S1，S△AED=S2，S△EAQ=S3，在（1）的条件下，判断S1+ S2=S3是否成立？并说明理由.

（一）赏题

1.熟悉——题目来源、背景

此题是2015年四川省资阳市中考数学试题.构图背景非常的熟悉，有K字形相似，有源于教材的正方形中常见的全等基本图形（浙教版《义务教育教科书·数学》八年级下册第127页第4题）.

2.巧妙——题目的设计意图

此题内容设计上很巧，把正方形中常见的全等基本图形与K字形相似利用点E有机结合，巧而不偏，新而不怪.其次，问题设计上也十分巧妙，虽然两道小题相对独立，但都用到了相似、全等、中点等数学知识，第（1）小题对第（2）小题有着承上启下的作用.

3.全面——题目的考查意图

考查内容全面，突出数学思想方法.此题涉及相似三角形、正方形、全等、勾股定理等知识点，涉及内容丰富.同时，考查的思想方法有数形结合、转化、化归等.

（二）析题

千里之行始于足下，任何一次成功解题的第一步都是审题.波利亚在《怎样解题》中指出，第一步是弄清问题.已知条件是什么？求证是什么？因此，在审题过程中，可以圈出以下几个关键词.

1.条件分析

（1）正方形ABCD，AEHG；

（2）DE=CF；

（3）E，F分别是边DC，CB上的点；

（4）E是CD的中点.

从条件正方形：我们可以联想到四条线段都相等、四个内角都相等且为90°，为找相等的边和角提供了条件.从条件DE=CF：已知不相邻的两条线段相等，我们可以想到全等三角形的对应边.从条件（3）：这是一个线段上的动点问题，注意是否存在分类讨论.从E是CD的中点：这是一个倍半关系.在平面几何中，中点问题常转化为以下三种方法来解决：其一，中线倍长法，构造全等三角形；其二，三角形中位线平行且等于第三边的一半，梯形中位线平行于两底，并且等于两底和的一半；其三，直角三角形斜边上的中线等于斜边的一半.只是这个条件与前面三个条件不同，只能用于第一个问题.

2.结论分析

（1）求证：Q为CF的中点；

（2）判断S1+S2=S3是否成立.

中点问题分析与前面类似不重复；判断S1+S2=S3是否成立：首先，若先看到相似基本图形，则可以联想到相似三角形的面积比等于相似比的平方这一性质；其次，看S1，S2，S3是否直接可求；再次，这是一个三面积之间和差关系的问题，在平面几何里常见的方法是截大补小，那么能否截大，将S3截分？能否补小，将S1和S2通过等面积的转化，转化到同一面积上？

教学启示：在日常教学中，在审题环节，教师要学会追第一问：你是怎么想的？要引导学生弄清已知和求证，学会分析条件、结论各自的作用，并积累一些经典条件的用法.例如，中点、两条线段相加等于第三条线段等；同时注意标图、圈画关键词，培养解题习惯和分析问题的能力.

3.解法分析

解题思路分析一般有演绎法、分析法和类比法.演绎法是根据条件所能推出的结论与要证结论的关系，在能够得出的结论中选择可能推出的待证结论的结论，再以这些结论为条件进一步推出新的结论，直至获得待证结论的过程.分析法是演绎法的逆推法，是执果索因的方法.类比法是通过回顾自己的解题经验，寻找待解命题与已解命题的条件、结论、图形或关系的相似性，原解题方法解决新问题的思路.因此，对于此题，我们可以得到以下大致思路如图2所示.

图2

关于第（1）小题选用了分析法.要证Q为CF的中点，已有E为CD的中点，可见如何证EQ∥DF是该小题的关键.再回头审视题设条件，题中有DE=CF和正方形ABCD，根据这两个条件易证得△CFD≌△DEA.于是得到了有关角与边的相等关系，其中有些结论对我们进一步求解有帮助，我们可以得到∠CDF=∠DAE.进而得到AE⊥DF.再根据题设中的以AE为边作正方形AEHG（即AE⊥EH），于是有EQ∥DF，从而我们可以顺利地解决第（1）小题.

关于第（2）小题使用了分析法.要判断S1+S2=S3是否成立，先看S1，S2，S3所对应的三个三角形，显然易得S1与S2所对应的△CQE∽△DEA，于是能得到有关边的比例关系，其中对我们继续求解有帮助，由于E是CD的中点，进而通过等量代换和变形可得再由∠QEA=∠C，从而可得S1与S3所对应的△CQE∽△EQA.既然S1，S2，S3所对应的三个三角形两两相似，那么我们可以得到由勾股定理QE2+AE2=AQ2，可得至此，我们可以圆满地判断出这一结论.

当通过以上审题步骤，若还找不到解题思路的时候，可以进行第二步.第二步是拟定计划.你以前见过它吗？你是否见过相同的问题而形式稍有不同？你能不能利用它？如果你不能直接利用它，那么你能不能做适当的变通？

关于第（1）小题类比法：以前没有见过，但见过条件类似而结论不同的证明题.题目如下.

如图3，已知E，F分别是正方形ABCD的边DC，CB上的点，且DE=CF.求证：AE⊥DF.

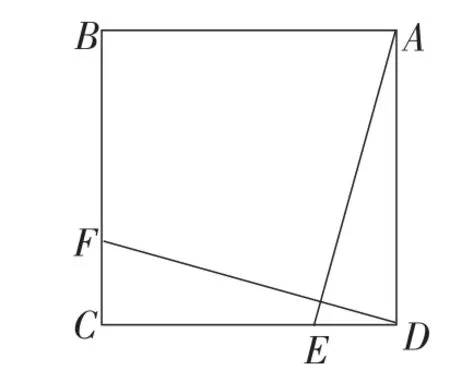
图3

如图4，已知E是正方形ABCD的边DC上的点，且满足AE⊥EQ交CB于点Q.求证：△CQE∽△DEA.

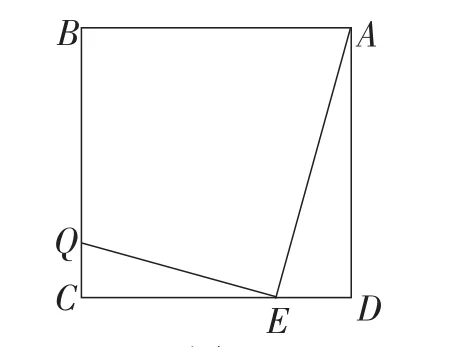
图4

通过利用这两个我们熟悉的结论，再加上条件E是CD的中点，第（1）小题得证.

第（2）小题类比法：可由相似基本图形，联想到相似三角形面积之比等于相似比的平方.可得由勾股定理QE2+AE2=AQ2，可得从而S1+S2=S3结果成立.

教学启示：对于复杂问题，教师要学会追第二问：你以前见过类似的问题吗？进而引导学生复杂问题简单化处理，有意识地引导学生多积累重要的基本图形；能分离出熟悉的基本图形；利用图形分离法解题；引导学生联想、迁移出相同或相似的图形、背景，积累解题经验与活动经验.

（三）解题

解题是波利亚所说的“第三步，实现计划”.根据上面的解法分析，我们可以得到以下解题方法.

解：（1）因为正方形ABCD，

所以AD=DC，∠ADE=∠DCF=90°.

又因为DE=CF，

所以△CFD≌△DEA.

所以∠CDF=∠DAE.

因为∠ADF+∠CDF=90°，

所以∠ADF+∠DAE=90°.

所以AE⊥DF.

因为正方形AEHG，

所以AE⊥EH.

所以EQ∥DF.

因为E为CD的中点，

所以Q为CF的中点.

解法1：（2）由题意，可证△CQE∽△DEA.

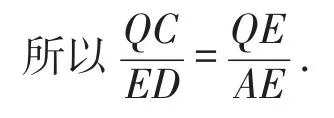
因为E是CD的中点，

所以ED=EC.

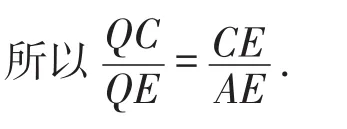
因为∠QEA=∠C，

所以△CQE∽△EQA.

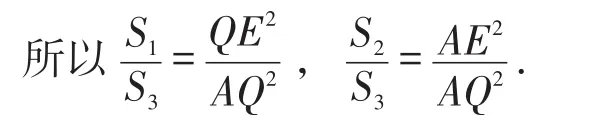
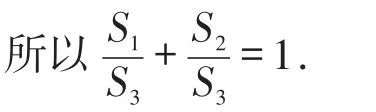
所以S1+S2=S3成立.

（四）思题

思题就是波利亚所说的“第四步，回顾”.这一环节很重要也很必要，对加深理解、巩固所学知识、启迪继续思考有着十分重要的作用.

1.是否可以用其他的方法导出这些结论

一题多解是数学的一大特征，在这个过程中能体验解决问题方法的多样性，发展创新意识，同时简约性又是数学的最大特征.第（2）小题用到两次相似及相似的性质与勾股定理解答，思维不容易形成，有没有更简约的方法呢？反思后对第（2）小题我们还可以有以下解题方法.

解法2：（2）由面积问题想到直接利用面积公式.

设CQ=a，

则易证S1=a2，S2=4a2，S3=5a2，从而使得命题得证.

解法3：（2）由面积的和、差想到割补法.

割大：如图5，过点E作EJ⊥AQ，交AQ于点J，通

因为QE2+AE2=AQ2，过证△CQE≌△JQE和△AED≌△AEJ，使得命题得证.

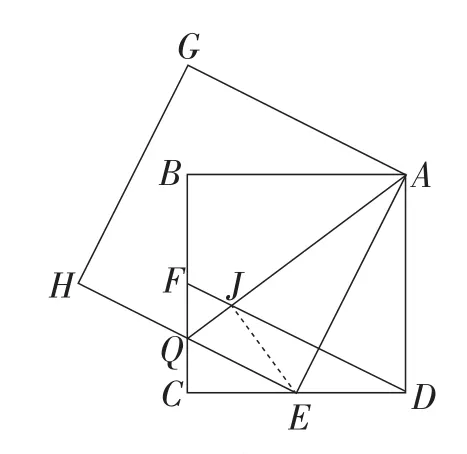
图5

补小：如图6，延长AD，QE，使其交于点I，转化为证△CQE≌△DIE和△AQE≌△AIE，使得命题得证.

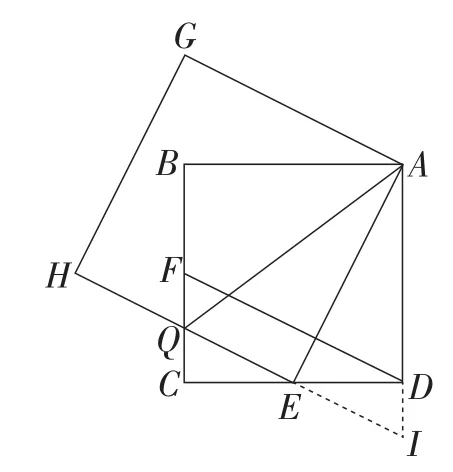
图6

2.是否具有一般结论或规律，使得命题得证

通过研究，还可以挖掘出一般结论.

（1）当E为CD的中点时，CQ的长度最大；

（2）当点E，F分别在射线DC，CB上运动时，始终有AE⊥DF；连接HF，四边形HFDE始终为平行四边形；G，B，Q三点始终共线等.

教学启示：在日常教学中，教师要学会追第三问：还有别的解法吗？进而引导学生进行解题后的反思.因为数学是一门高深的学科，很多题目的解题过程都不是唯一的，是可以有多种方法来解答的，这时就需要教师及时的补上一句：是否还有其他的解法，你是怎么想的？让学生不断地进行反思，在反思中将数学的知识点、方法理解透彻，同时培养学生的学习兴趣和发散性思维.最后教师也要学会追第四问：你还有什么问题或发现？进而引导学生提出问题或发现一般规律，培养学生提出问题的能力和归纳问题的能力，进而进行探究和创新.

（五）变题

变式教学在我国数学教学中发挥了很重要的作用.下面从变条件和变结论两方面来说一说此题的变式.

1.变条件

（1）改变图形的形状.

如图7，若把正方形ABCD，AEHG变为菱形ABCD，AEHG，其他条件不变，上述两道小题的结论还成立吗？

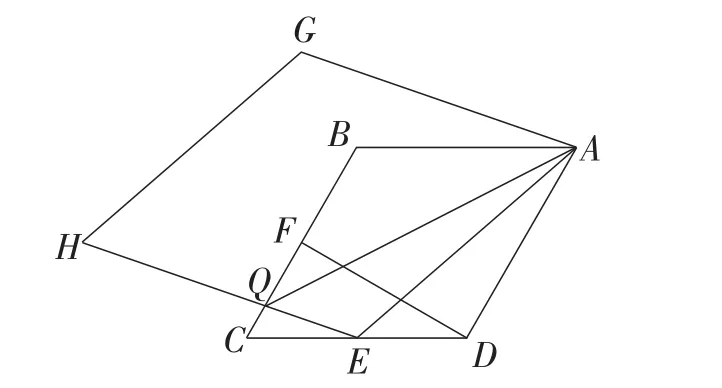
图7

显然，把正方形ABCD，AEHG变为菱形ABCD，AEHG后，DF与QE之间不存在必然的平行关系了，因此第（1）小题结论不一定成立了.第（2）小题，去除多余的图形，不难发现，这也是我们常见的一个基本图形（如图8），利用旋转（如图9）发现仍然有S1+S2= S3成立.

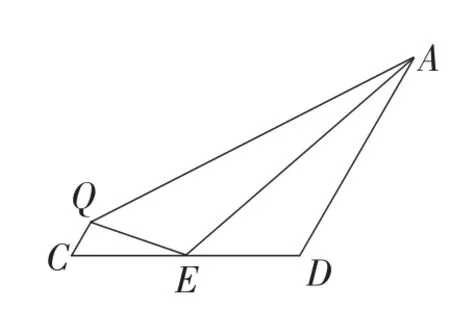
图8

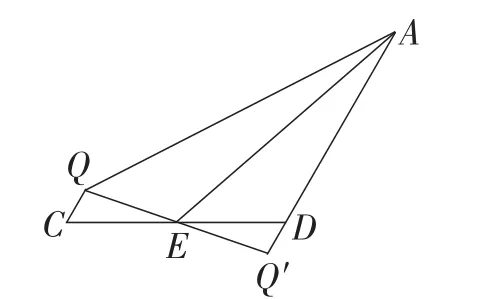
图9

（2）改变点E的位置.

若点E运动到满足时，如图10，其他条件不变，上述两道小题的结论还成立吗？若不成立，你有什么新的发现？

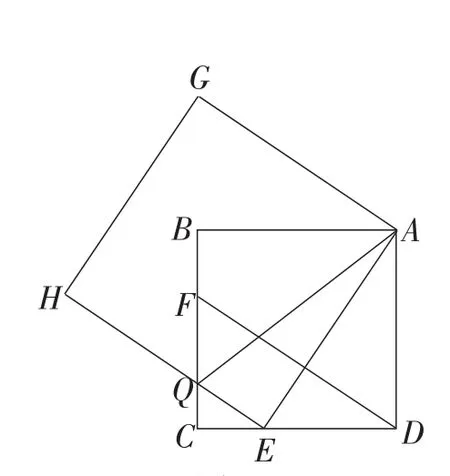
图10

显然无论点E如何运动，始终有AE⊥DF，当满足CD时，则因此，第（1）小题的结论变成了第（2）小题的结论，借助于前面的解法，如图11，我们不难发现S1+S2=S3已不成立，但S1，S2，S3之间有了新的数量关系，即2S3=4S1+S2.

继续改变点E的位置，若点E运动到满足CE=时，则第（1）小题的结论变成了第（2）小题S1，S2，S3之间新的数量关系为（n-1）S3=（n-1）2S1+S2.

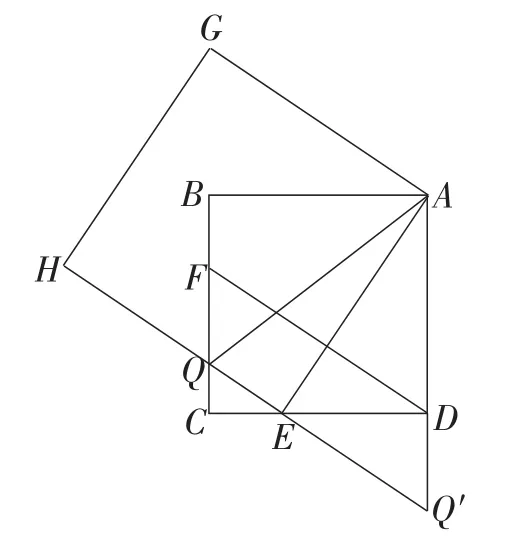
图11

以上几个变式虽然从特殊（图形、位置）发展到了一般，但用到的知识点没有变、解题方法没有变，因此在没有增加学生认知负担的同时又巩固了解题方法，开拓了思维，一举多得.

2.变问题

（1）与二次函数结合.

若正方形ABCD的边长为1，当点E从点D向点C运动的过程中，线段CQ的长度是否具有最大值？

（2）与圆结合.

当点E在直线CD上任意移动时，设正方形ABCD的边长为a，AE与DF交于点P，求BP的最小值.

初中数学中最常见的最值一般分为两类：一类为几何中的共线型最值；一类为函数型最值.此处通过变问题，让学生体验了这两类最值，感受数学之最.

教学启示：在日常教学中，教师要学会变式.通过改变（弱化）条件或结论，引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，帮助学生克服简单的机械重复，提高解题效率，培养灵活的解题能力和特殊到一般的数学思想.

三、说题收获

俗话说，工欲善其事，必先利其器.说题是一种非常有效的提高教师业务水平的途径，教师作为学生学习的组织者、引导者与合作者，可以从赏题、析题、解题、思题、变题这几方面研究入手，在日常教学中不断地积极钻研教材与学生，不断地积累教学经验，并进行有效追问，不断地从实践到认识、再从认识到实践，多次反复，进而促使自身发展.这样才能更有效地去引导学生、帮助学生、培养学生，真正达到“轻负高质”这一目标.

［1］罗增儒．数学解题学引论（第2版）［M］．西安：陕西师范大学出版社，2001．

［2］桂文通．好题多磨，磨出精彩［J］．中学数学教学参考（中旬），2015（1/2）：114-116．

［3］沈岳夫，张乃池．一道月考试题的解法探析及拓展［J］．中学数学教学参考（中旬），2013（5）：27-29.

［4］吴光潮．构建“知识积件模型” 提升合情推理能力［J］．中学数学教学参考（中旬），2015（1/2）：58-60．

2016—09—14

来林芳（1978—），女，中学一级教师，主要从事初中数学教学与解题研究.