由一道高考题谈定式教学

陈宇峰

(江苏省无锡市玉祁高级中学，214183)

由一道高考题谈定式教学

陈宇峰

(江苏省无锡市玉祁高级中学，214183)

(1)求椭圆的方程;

(2)设A, B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.

(ii)求证:PF1+PF2是定值

(2)(i)设∠AF1F2=θ,则

∠BF2F1=π-θ.

记AF1=m,BF2=n,则

接下来分别在∆AF1F2与∆BF1F2中应用余弦定理，得

(*)

两式一加又一减，得

(ii)根据AF1∥BF2,得

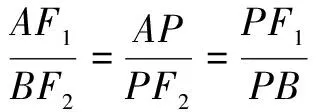
θ≠90°时,由(i)的(*)式中两式相除并整理得

以上解法来源于一个定式(图2),即在两个三角形中,对于两个互补的角使用两次余弦定理,这也是一种“算两次”的思想方法．

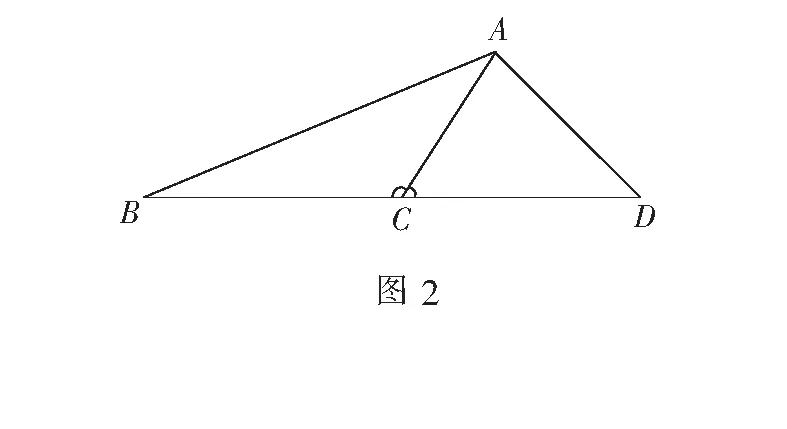
运用这个“定式”可以求已知三角形的中线长度,也可以推导出平行四边形四边平方的和等于其对角线的平方和这个结论,还可以求圆内接四边形的对角线长度等等．

再举一例:

解析 在本题椭圆这个情境中，有焦点三角形,只要设左焦点为M,连结AM,BM就产生了以上“定式”.设直线的倾斜角为α,则∠MFA=α,∠BFM=π-α.设AF=3m,BF=m,分别在∆BMF,∆AMF中使用余弦定理进行算两次，得

两式相减，得到

-8m2+8am=-8m2+16cmcos α,

所谓定式,主要是指一些特定的图形、形式、结论、方法或固定的数学模型等.如下面的例子:

(1)平几中的直角三角形或立体几何中的长方体(或正方体)的一角,即“墙角”；

(2)分式齐次式；

(3)三角形中结论:tan A+tan B+tan C=tan Atan Btan C；

(4)直线与圆的问题中多运用“d” 即圆心到直线的距离，等等.

其实，定式教学是很早就被谈及的数学教学的一个有效手段,与之相对应的变式教学也是教师们津津乐道的．定式教学是属于定势教学的一种手段.所谓定势教学，简而言之即强调学生利用已提炼过的思维定式进行有效解题的一种教学活动．

特别地对于高三数学的复习,由于时间紧任务重,有效性和针对性就尤其重要.利用定式教学可以对某些特定的对象和目标进行采集，形成小专题复习,这无疑能够取得成效．