浅谈定向思维和发散思维能力的培养
2017-01-16杜根华
杜根华
(江苏省无锡市第六高级中学,214000)
浅谈定向思维和发散思维能力的培养
杜根华
(江苏省无锡市第六高级中学,214000)
现代教育重视发展学生的思维能力,思维能力的培养会影响学生的一生,思维能力的培养是数学教育的价值得以真正实现的理想途径.按思维的方向不同,思维可分为定向思维与发散思维.定向思维和发散思维是思维方式的两种不同形式,定向思维是人们在掌握固有知识的前提下循规蹈矩的固定的思维方式;发散思维则是定向思维的深化与发展.两者之间有着必然的联系:定向思维的形成到发散思维的开启,它是一种螺旋式的上升,具有科学的韵律.
思维是人们对客观事物间接的、概括的正确反应,它是以表象、概念、判断、推理形式反映客观世界能动的过程.
在今天的数学教学中,学生思维能力的培养显得十分重要.那么,又如何培养思维能力呢?这就要求我们在教学中,要培养学生会思维,能思维,积极的思维,科学的思维.为达到这一目的,数学教学中就要注意学生思维能力的培养,其具体模式为:先形成定向思维,再利用定向思维的积极性,克服其消极性,形成发散思维,最后发散思维进一步深化,实现螺旋式上升.
一、高中数学定向思维的培养
定向思维是人脑对事物本质和事物之间规律性关系概括的间接的反映,以固定的方式去思考和解决问题.
思维定势有助于学生对解决的问题做出迅速的反应,并对问题做到较清楚的认识和理解,同时为解决该问题提供一个程序,使学生有可能按程序将其解决.
一般在新授课时,就要设法让学生形成思维.例如,在解答高中数学计数原理试题时,我们一般拿出常规的方法:不相邻问题用插空;相邻问题用捆绑;定序问题用除法;还有老师告知学生做题时一般都是先选后坐位置.可如果你因循守旧,不知变通的话,那就错了.
例1 有6个球,其中三个黑球,红,白,蓝球各一个,现从中取出4个球排成一列,共有多少种不同的排法?
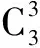
定向思维虽然有局限性,但可以提供思考的方向和一般的解题方法或者是一套解题程序.有了这套程序,虽不能解决所有类似的问题,但学生有了初步的思考方向和一般的解题方法,可最大限度地消除学生不敢动笔的现象,这对学生有一定的好处.比如说,在学生练了很多概率题时他就有一定章法可寻,思路就比较清晰,而且知道考察哪些知识点.下面是笔者最近给学生做的一道题,得分率比较高.这是为什么呢,我想可以解释为学生思维已经有了一定的培养,得到了提升.
例2 某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
解析 本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力.第(1)问直接利用分层统计原理即可得人数;第(2)问注意要用组合公式得出概率;第(3)问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求出概率.
解 (1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记A表示事件:从甲组抽取的工人中恰有1名女工人,则
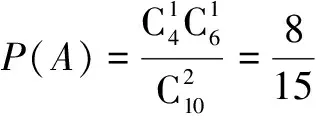
(3)Ai表示事件:从甲组抽取的2名工人中恰有i名男工人,i=0,1,2,Bj表示事件:从乙组抽取的2名工人中恰有j名男工人,j=0,1,2,Ai与Bj独立,i,j=0,1,2,且B=A0·B2+A1·B1+A2·B0,故
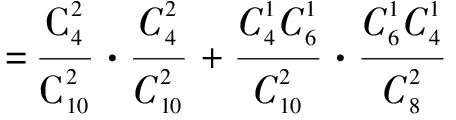
定向思维的培养有益处也有坏处,那就需要我们把定向思维发展到一定程度,提高思维方式的培养——发散思维,否则就会产生消极影响.
二、定向思维过渡到发散思维的培养
发散思维是一种高层次的思维形式,其形成非一朝一夕可以完成,它需要由熟到巧的过程,也要教师的不断培养.因此,我们在教学中应注意学生的新奇感,多来几个假设,多问几个为什么,提供一题多解,一题多变,达到举一反三之境界.
在教学过程中,用多种方法,从各个不同角度和不同途径去寻求问题的答案,用一题多解来培养学生的发散思维.
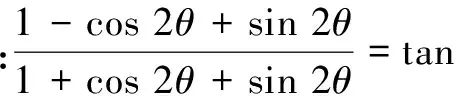
证法1 (运用二倍角公式,统一角度)
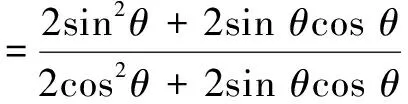
证法2 (逆用半角公式,统一角度)
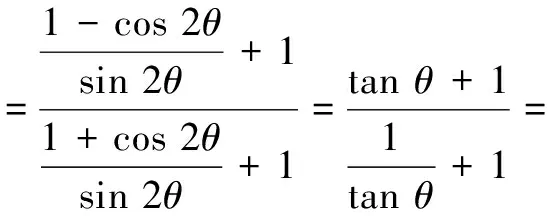
证法3 (运用万能公式,统一函数种类)
设tan θ=t,则
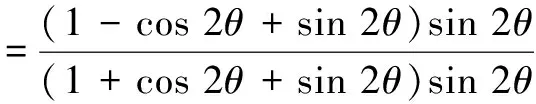
证法5 (变更问题法)只要证下式.
(1-cos 2θ+sin 2θ)sin 2θ
=(1-cos 2θ)(1+cos 2θ+sin 2θ)
即可.
通过一题多解引导学生归纳证明三角恒等式的基本方法:(1)统一函数种类;(2)统一角度;(3)统一运算.
一题多解可以拓宽思路,增强知识间联系,学会多角度思考解题的方法,引导学生对问题的解法进行发散思维.
当然,我们不仅可以用一题多解去培养发散思维,而且可以利用结论或条件的改变来培养学生的发散思维.
