例谈分类讨论思想在函数教学中的三重境界
2017-01-12江苏省南通市通州区金沙中学季汉杰
☉江苏省南通市通州区金沙中学 季汉杰
例谈分类讨论思想在函数教学中的三重境界
☉江苏省南通市通州区金沙中学 季汉杰
众所周知,中学数学教学从培养学生双基开始、到综合知识的整合运用、再到思想方法的提炼渗透,是中学数学教学的三个基本步骤.对于学生而言,数学思想方法的提炼和渗透是最难实施的,从一线教学的实践来看,不少学生对于问题的转化、如何恰当地使用合适的思想方法介入都是比较茫然的.
以下面的问题为例,设函数f(x)=x2+ax+b(a,b∈R).
(1)若b=1,函数f(x)在[-1,1]的值域是[m,n],求函数h(a)=n-m的表达式;
笔者调查过学生的试卷,也请学生回顾了解题时的思路,学生给出的回答是:我知道是分类讨论思想,但是我不知道怎么分?好像很乱,没法下手.的确对于学生来说,其对分类讨论思想仅仅是字面的了解,“如何正确分类?”“为什么要分?”“怎么分?”“不分行不行?”等等都是极其模糊的.本文从三个角度来谈谈,分类讨论思想在教学应该如何渗透,与大家一起交流.
一、辨别为何要分类
在数学问题处于定值范畴时,我们很少会想起分类讨论思想,这也是初中生所涉及的大部分数学问题,以定值型问题为主.而高中数学最主要的是变量思想的渗透,因为变量问题才是生活中无处不在的数学模型,这就是函数概念为什么是高中数学最重要的概念的原因吧.但是学生对于变量思想下的数学问题往往缺乏动态的认知,因为缺少了这种认识,淡忘了分类意识,导致学生对很多问题没有为什么要分类的想法.
问题1(1)求函数f(x)=x2在区间[-1,1]上的最小值;(2)求函数f(x)=x2-2ax+a(a∈R)在区间[-1,1]上的最小值.
分析:问题(1)学生解决较为轻松,显然在函数确定的前提下,函数在闭区间上的最小值易求,如图1.将问题转化为动态情形下,笔者给高一学生尝试这样的问题,不少学生认为当x=a时,f(x)min=f(a)=a-a2,因为初中归纳二次函数时最(大)小值是在对称轴处得到的!还有学生煞有介事的问错误的原因在哪里?叫人哭笑不得.笔者以为:这是学生对于含参二次函数缺乏动态思考的原因,观察函数f(x)=x2-2ax+a模型,显然影响这一函数最重要的因素是其对称轴的移动,如图2,将其从左至右进行动态思考,找到了函数在区间[-1,1]上最小值为何要分类讨论的原因.

图1
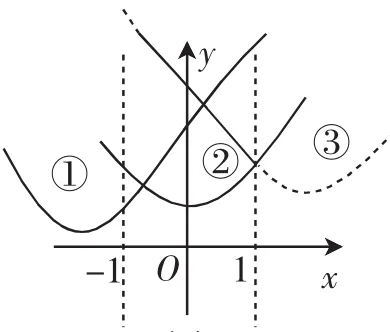
图2
说明:对于二次函数在闭区间上最小值的分类讨论是非常常见的,通过上述问题1,我们可以总结二次函数f(x)=ax2+bx+c(a>0)在闭区间[m,n]上的最小值是以对称轴落在(-∞,m]内,落在[m,n]内,落在[n,+∞)内进行合理的分类讨论;若将问题演变为最大值,则显然是以对称轴落在和进行分类讨论;若将问题演变为最值求解,则将前两种问题结合在一起,以对称轴落在(-∞,m],四类进行讨论,这种函数图像动态运动形成的最值是为什么要分类的主要原因.
二、思考如何来分类
对于函数中的变量进行分类讨论如何切入,是学生学习分类讨论思想的一个难点.学生在处理函数问题时候,往往遇到变量位置的不同,当出现在不同位置的变量进行讨论时,如何合理的来分?合理的找到切入点,是解决这些问题的关键.
问题2(变量分类的介入题组).
(1)二次项系数介入的讨论.
题1 已知函数f(x)=plnx+(p-1)x2+1,当p>0时,讨论函数f(x)的单调性.
当p≥1时,f′(x)>0,故f(x)在(0,+∞)单调递增.
说明:导函数的分子是二次函数,对于二次项系数和一次项系数均含有参数p的情形下,首先可以从二次项系数切入去分类,因为对于开口方向的讨论是二次函数讨论的第一切入口.教师在教学中对于二次函数f(x)= ax2+bx+c(a≠0)字母的讨论,应该从a、b、c顺序介入,其代表的含义开口讨论、对称轴讨论、判别式的讨论.看下一个问题:
(2)动态对称轴介入的讨论.
解析:由已知得g(x)=ln(x+1)+3-(-2x2+4ax+3)= ln(x+1)+2x2-4ax,
因此实数的取值范围是a≤0.
说明:显然对于本题导函数中的分子部分,二次项系数为定值前提下,对一次项系数分类进行介入,正是二次函数中对称轴变换的讨论.
(3)判别式变换介入的讨论.
题3 已知函数f(x)=x2-x+alnx(a>R),讨论f(x)在定义域上的单调性.
说明:本题导函数中的二次函数部分,二次项系数和一次项系数均为定值,对于常数项的讨论恰为其判别式的分类介入,因此以判别式讨论本题成为解决问题的关键.
三、学会减少分类
掌握了分类讨论的前两种层面后,学生对于含有参量的问题有了基本的绝佳思路:即找到分类切入点,进而讨论解决.随着问题难度的增加,分类讨论的复杂程度也会随之进一步增加,有时候会出现很多种分类的切入以及多达数十种情形的分析,这样就失去了问题考查的意义,试想在有限的时间内不可能用多种或数十种分类去解决一个问题.因此教师教学中对于分类讨论思想的最高境界就是引导学生找到更为合理的切入点,甚至达到学习分类讨论,更能站在系统的高度不进行分类就能解决含参问题.
问题3解关于x的不等式
分析:本题是含参不等式的求解,有兴趣的读者可以百度其参考答案,共计分为四大类十六小类进行分类讨论,笔者以为这样的讨论教学是“误人子弟”的!也是毫无意义的!站在系统的高度,笔者认为,需要对含参问题作减少分类的思考,因此将不等式问题转化为函数问题,利用数形结合思想结合解决,即问题转化为:函数g(x)=|x-1|-1的图像不高于f(x)=的图像,求实数a的取值范围.借助数形结合思想,我们将问题转变为动态函数与定函数之间的图形比较,从直观思维角度来说,这大大降低了问题的抽象性,也将分类的情形大幅作出了删减.
①当a=0时,即y=|x|,如图3所示,易知y=|x|≥y=|x-1|-1对一切x∈R成立.
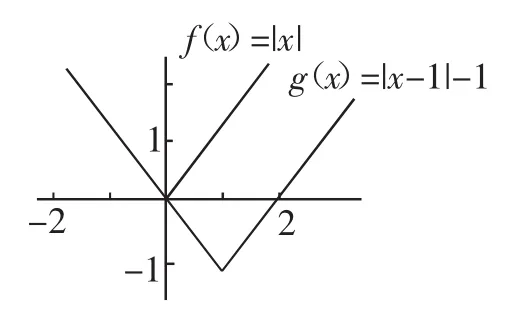
图3
②当a<0时,即y2-x2=-a(y>0,a<0),如图4所示,其图象为双曲线的上半支,则对一切x∈R成立.
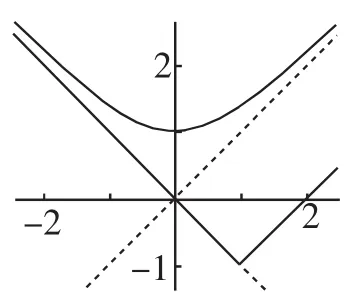
图4
③当0
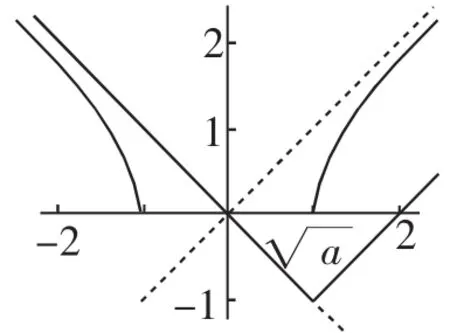
图5
④当a>4时,情形同③,如图6所示,左支不成立,右支与y=|x-1|-1有一交点(联立方程2),可得则当时,原不等式成立.
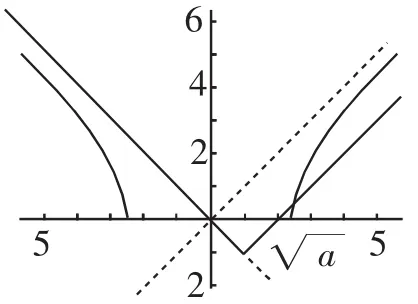
图6
说明:相比原解,笔者引导学生思考了如何简化分类讨论的步骤,本题借助了数形结合思想.笔者认为学会解题不仅是耐心,也需要一点思考的方向,试想若本题从代数角度去讨论不等式,那么其对于学生思维的启发是很有限的,更多达数十种的讨论也让师生置身于无意义的讨论之中,导致学习效果的下降和兴趣的丧失.
总之,分类讨论思想是高中数学必不可少的重要思想方法,教师教学从高一开始渗透,并逐步加深讨论的复杂程度和难度.但是在教学的同时,我们也要多思考下面不同层级的问题:
(1)学生为何不会分类?为何没有想到这里要分类?我们应该如何教学?
(2)学生知道分类讨论,为何无法将问题正确分类?学会了分类为何在思考切入角度上还不足以一击命中?
(3)是不是每个含参问题都是直接从分类入手的?有没有简化分类的方式或思考?能引导学生找到合理的途径进而减少分类的情形才是分类讨论教学最高的境界,甚至可以将问题转化为不需要分类去处理,才是我们分类讨论思想教学的最终目的.给出一个思考:设实数a,b使方程x4+ax3+bx2+ax+1=0有实根,求a2+b2的最小值.有兴趣的读者可以试试,如何不用分类讨论就解决问题呢?答案参考文[3].
1.沈科.数学高考难题破解与思想方法的联系[J].中国数学教育,2014(8).
2.周刚强.高中生数学学习困难的归因分析及对策研究[J].数学教学通讯,2012(10).
3.刘薇.一道竞赛题的三种解法[J].高中数学教与学,2010(7).
