化归转化思想解题例说——以一道线性规划综合问题为引例

☉江苏省南菁高级中学 张丽娟

化归转化思想解题例说
——以一道线性规划综合问题为引例

☉江苏省南菁高级中学 张丽娟

在数学解题中，如果对原问题直接求解不易入手，此时不妨将原问题变换为我们熟悉的、易于解决的问题来处理.这就是化归转化思想，即将一种研究对象在一定条件下转化为另一种研究对象的思想.下面就化归转化思想的应用举例分析.

例1已知点A（a，b）与点B（1，0）在直线3x-4y+10=0的两侧，给出下列说法：

①3a-4b+10>0；

其中，所有正确说法的序号是_________.

本题以线性规划为背景，设置多个结论，综合性较强，解题中要善于根据题目条件将问题进行等价转化求解.此类问题能有效考查考生分析问题与解决问题的能力.

一、善于把握问题的本质

对于①，利用不等式所表示的平面区域的概念，将点B（1，0）的坐标代入直线3x-4y+10=0所得值大于零，故3a-4b+10<0.①错误.

评析：判断一个点是否在某个不等式所表示的平面区域内，可直接将点坐标代入不等式方程中，若满足不等式，则该点在所给不等式的区域内，否则不在该区域内.充分把握不等式所表示的平面区域的本质，即可顺利求解.

变式1（2014年新课标全国卷Ⅰ）不等式组的解集记为D，有下面四个命题：

p1：∀（x，y）∈D，x＋2y≥-2；

p2：∃（x，y）∈D，x＋2y≥2；

p3：∀（x，y）∈D，x＋2y≤3；

p4：∃（x，y）∈D，x＋2y≤-1.

其中的真命题是（ ）.

A.p2，p3B.p1，p2

C.p1，p4D.p1，p3

解析：不等式组所表示的平面区域如图1所示，在图中画出命题1中不等式x＋2y≥-2所表示的平面区域，易知此区域包含区域D，所以命题p1正确.同理命题p2正确，p3、p4错误.答案为B.

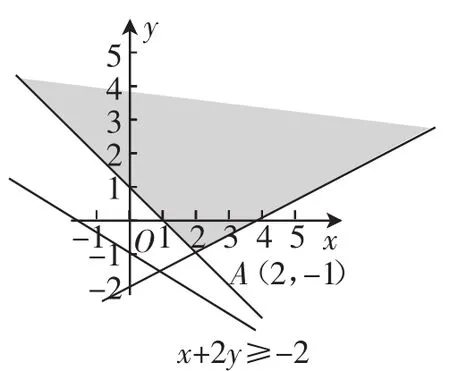
图1

二、拓展由此及彼的洞察力

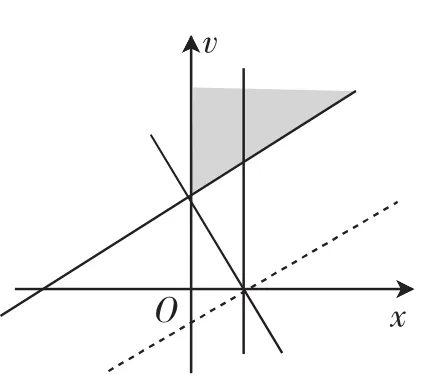
画出可行域（如图2所示），因为3a-4b+10=0所在的直线为虚线，所以z=a+b既不存在最大值，也不存在最小值.故②错.

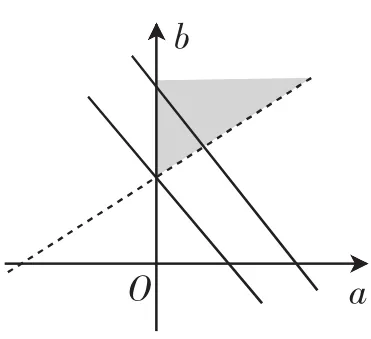
图2

评析：若不等式中含有等号，则其区域边界直线为实线；若不含等号，则其边界直线为虚线.

变式2（2015年山东卷）已知x，y满足约束条件若z=ax+y的最大值为4，则a=（ ）.

A.3 B.2 C.-2 D.-3

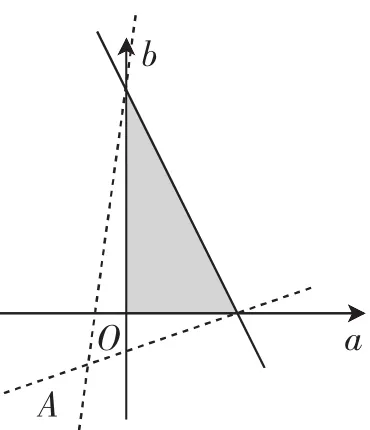
解析：由z=ax+y得y=-ax+z，画出不等式组表示的目标区域，如图3，借助图像可知：

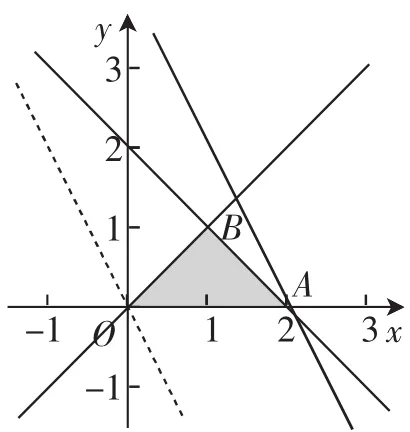
图3

当-a<-1，即a>1时，在x=2，y=0时有最大值2a=4，a=2，满足a>1；

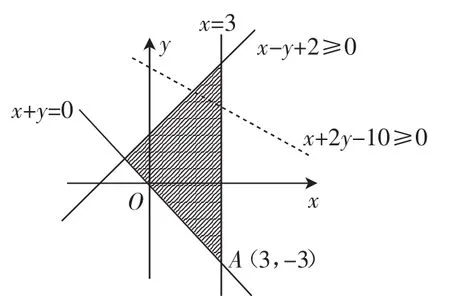
当-1<-a≤0，即0

当0≤-a<1，即-1

当-a≥1，即a≤-1时，在x=y=0时有最大值0，不符合题意.

答案选B.

三、善于寻找命题的等价形式

评析：在线性规划问题中，目标函数一般有两种类型，一种是线性型，一种是非线性型.对于非线性型，除本小题中的两点间距离型以外，还有点到直线的距离型.即对于目标函数为形如z=|Ax+By+ C|（A、B不同时为0）型时，求解方法是先将其变形为z=（A、B不同时为0），然后利用的几何意义：动点P（x，y）到直线Ax+By+ C=0的距离求出最值，最后再乘以求解问题.

变式3已知实数x，y满足约束条件求 z=|x+2y-10|的最大值.

解析：由条件画出可行域，如图5所示，z=|x+2y-10|=根据图形易得A点到直线x+2y-10=0的距离最大，根据方程组可求得A（3，-3），所以

图5

四、把握结论与条件的关系化生为熟

综上所述，正确结论为③、④.

评析：在处理与目标函数为斜率型的线性规划问题时，要注意斜率的范围.当倾斜角为时，斜率k∈［0，+∞）；当倾斜角为时，斜率k∈（-∞，0）；当倾斜角为时斜率不存在.如，当倾斜角α∈时，学生易错误地认为斜率k∈［-1，1］.正确答案应为［1，+∞）∪（-∞，-1）.若斜率k∈［-1，1］时，倾斜角的范围是

变式4定义在R上的函数（fx）满足（f4）=1，f（′x）为（fx）的导函数，已知y=f（′x）的图像如图7所示，若两个正数a，b满足f（2a+b）＜1，则的取值范围是（ ）.

图7

解析：由导函数的图像知f（x）在区间（0，+∞）内单调递增，又f（2a+b）＜1且f（4）=1，所以2a+b<4，结合a，b>0，构造不等式组进而将问题转化为线性规划问题.

图8

总之，解题时从考查问题的结构、特点入手，横向联想与之形似的某些熟知情境及处理方法，或纵向联想类似解决过的问题及解决方式，这样就能快速地找到解决问题的突破口.