“空间运动”与“圆锥”的“不解之缘”
——由2016年浙江高考谈“动态”立体几何教学建议
2017-01-12江苏省如皋市第一中学吉俊杰
☉江苏省如皋市第一中学 吉俊杰
“空间运动”与“圆锥”的“不解之缘”
——由2016年浙江高考谈“动态”立体几何教学建议
☉江苏省如皋市第一中学 吉俊杰
“动态”充满着神奇,孕育着创造,动态性问题渗透着运动变化的观点,是立体几何的一大难点.所谓“动态”性立体几何题,是指在点、线、面运动变化的几何图形中,探寻点、线、面的位置关系或进行有关角与距离的计算.[1]当前高考“动态”立体几何的命题趋势逐渐由“关注学生学习结果”转向“关注学生学习过程”,更加注重与其他知识交汇融合,尤其是浙江省高考中的“动态”立体几何问题,更是与“圆锥”结下了“不解之缘”.浙江省的“动态”立体几何问题除考查立体几何基本知识点与基本思想方法以外,更注重对学生直观想象核心素养与综合运用知识能力的考查.学生在解决这类问题时,总存在着一定的心理和思维方面的困惑或障碍,下面笔者就结合近几年高考的命题趋势,谈谈此类问题的教学建议.
一、又是一年芳草绿,依然十里杏花红
又是一年高考时,今年浙江高考数学文理卷上各有一道关于“动态”立体几何的题目,而且两道题都与“圆锥”存在紧密联系.
例1(2016年浙江高考文科第14题)如图1,已知平面四边形ABCD,AB=BC=3,CD=1,AD=∠ADC=90°.沿直线AC将△ACD翻折成△ACD′,则直线AC与BD′所成角的余弦的最大值是______.
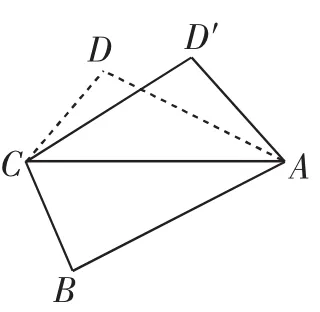
图1
解析:此题“动态”十足,属于比较常见的翻折问题,但按照一般求空间角的思路,不论是利用几何法作出空间角,还是利用坐标法求出角,解题过程都会比较复杂.如果关注“翻折”运动的特点,发现动点D做圆周运动,线段CD的运动轨迹构成一个圆锥(以AC为轴).
如图2,过点D作DH垂直AC于点H,点D在以H为圆心,DH为半径的圆上运动.在D点运动的过程中,直线AC与BD所成角为直线BD与圆面所成角的余角.因此,问题等价于求直线BD与圆面所成角的正弦值的最大值.
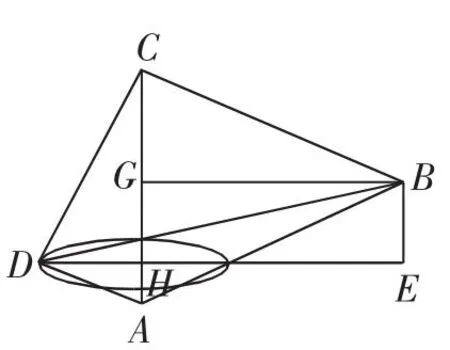
图2
例2(2016年浙江高考理科第14题)如图3,在△ABC中,AB= BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是_______.
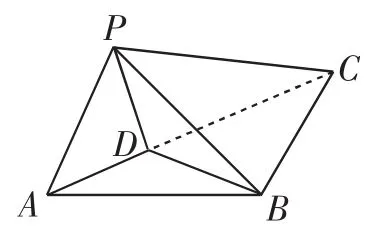
图3
解析:此题“运动”特点不明显,人们很难把它与“动态”立体几何联系起来,而是把它当作一般的求体积问题来处理.设AD=x,然后把四面体的体积表示为x的函数,进而转化为函数最值问题.这种解题思路尽管能求出结果,但过程烦琐,运算复杂,“小题大做”,得不偿失.
若用“运动变化”的视角重新审视题目条件与结论,我们对上述四面体中的点、线、面的关系会有新的认识,具体如下表所示:

静止 运动点点A、B、C 点P、D线 AB=BC=PB=2,AC=2 3■ PB与面ABC的夹角、DA=PD面面ABC 面BAP、面BPC、面APC
由“AB=BC=PB=2”联想到以B为顶点,BA、BC、BP为侧棱的三棱锥模型;“BP运动中长度保持不变”,那么PB可以看成B为顶点的圆锥的母线.于是,我们就可以在四面体的基础上构造如图4所示的圆锥模型,可以得到此题一种“特殊”(近似)解法.
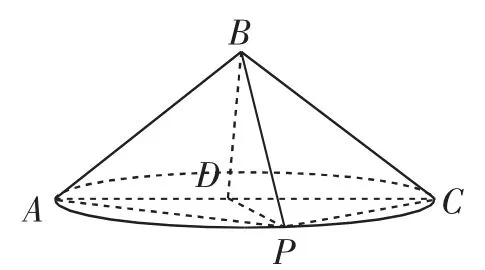
图4
要使四面体PBCD体积最大,需要高与底面S△PCD最大;当面ABC与底面垂直时高取得最大值1,此时AP⊥PC,如图5所示,设∠PAD=α,由DA=PD得∠DPA=α,则所以所以D是 AC的中点,此时满足因此要使S△PCD最大,只需S△PAC最大.显然,当PA=PB时,S△PAC取到最大值为此时所以VB-PCD的最大值为
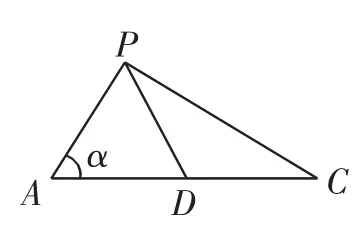
图5
构造圆锥模型的最大好处就是容易确定动点P的位置及运动轨迹,容易发现隐含的几何性质,从而使解题过程得到优化.
二、千歌百舞不可数,就中最爱霓裳舞
无独有偶,2015年的浙江数学高考文、理也各有一道“动态”立体几何题,而且也都与“圆锥”有关.
例3(2015年浙江高考文科第7题)如图6,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PBA=30°,则点P的轨迹是( ).
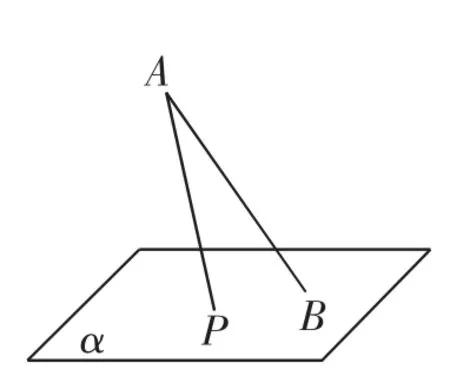
图6
A.直线 B.抛物线
C.椭圆 D.双曲线的一支
解析:如图7,P点的轨迹为以斜线段AB为旋转轴,母线与AB所成的角为30°的圆锥面,因直线AB与平面α所成的角为60°,故平面沿垂直于母线AD方向去截,截得的截面显然为椭圆.
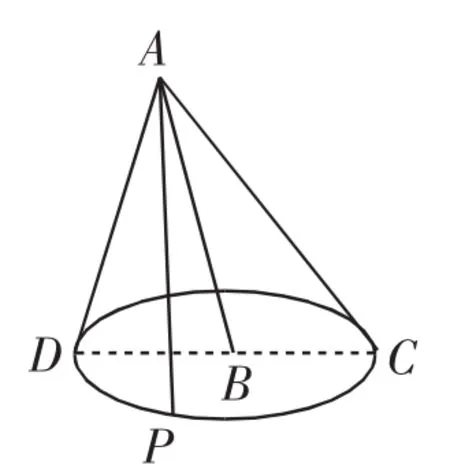
图7
例4(2015年浙江高考理科第8题)如图8,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( ).
A.∠A′DB≤α B.∠A′DB≥α
C.∠A′CB≤α D.∠A′CB≥α
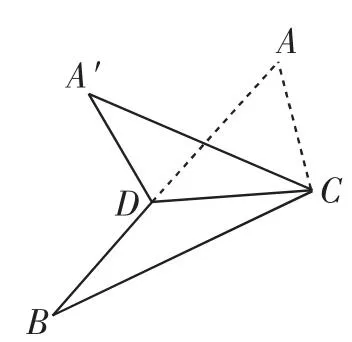
图8
解析:对于选择题而言,用特殊位置法也能得到答案,但无法触及问题本质.事实上,过A点作AP⊥DC,垂足为P,延长AP交BC与点R,连接A′P,则∠A′PR为二面角A′-CD-B的平面角,△A′CD绕直线CD转动,由此可以构造圆锥模型,如图9,A′点在共底面圆锥C-P、D-P的底面上转动,在等腰△PAA′中,易知∠A′PR=2∠PAA′=α;在等腰△DAA′中,∠A′DB=2∠A′AD.因为AD>AP,所以等腰△DAA′的腰长比等腰△PAA′的长,根据大边对大角,可知∠A′AD>∠PAA′,所以∠A′DB≥α.
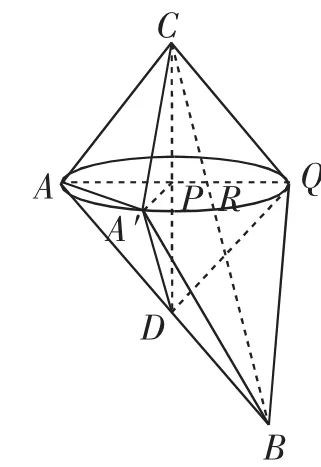
图9
通过构造圆锥模型,我们不仅圆满地解决了问题,并且还发现“D是线段AB的中点”的条件其实是多余的,没有这个条件结论照样成立.
纵观近10年的浙江数学高考试卷(如下表所示),不难发现几乎每年都有关于“动态”立体几何的题目,其中很多题目都与“圆锥模型”存在着“不解之缘”,只要“圆锥模型”一出手,问题的本质就暴露无遗.
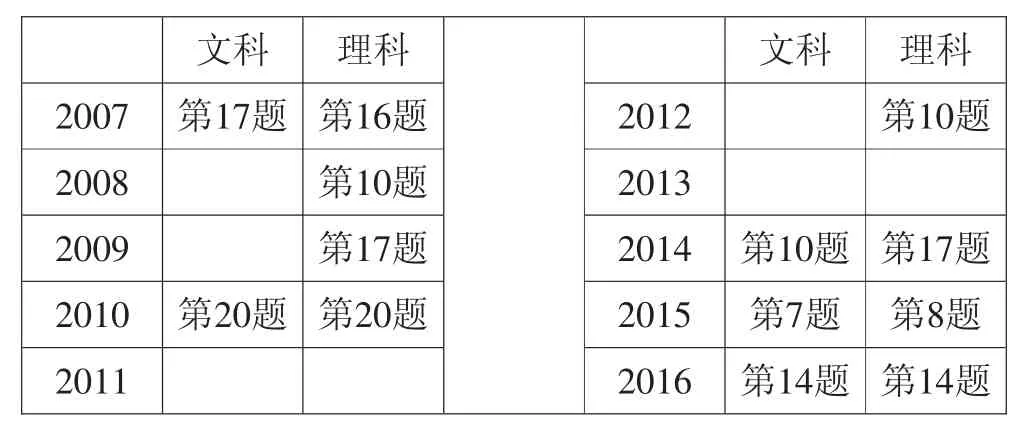
?
罗增儒教授曾说:“以能力立意命题,利于题型设计,易形成综合自然、新颖脱俗的试题.”给静态的立体几何题赋予了“动态”的活力,使题意更加新颖、解法更加灵活、思维更加广阔.也正因为某些点、线、面位置的不确定,成为考生进行常规思考、转化的障碍,但又因为其是可变的、开放的,更有助于学生空间想象能力及综合能力的培养.这应该就是“动态”立体几何备受青睐的原因.那么,教师该如何有效地开展“动态立体”几何问题的教学呢?
三、不畏浮云遮望眼,只缘身在最高层
1.发展“直观想象”核心素养
综上可知,“动态”立体几何重在考查“直观想象”核心素养.所谓的“直观想象”是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.在解决“动态”立体几何问题中,首先通过直观感知数学对象的几何属性,初步形成判断与理性思考,然后通过几何直观、动态想象等思维过程准确把握数学对象的全貌和本质,从而找到问题的突破口,实现“化繁为简”、“事半功倍”的效果.直观想象是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.当然,“直观想象”素养是建立在针对几何图形长期有效的观察和思考的基础之上,既有相对丰富的经验积累,也有经验基础之上的理性的概括和升华,因此,在平时教学中要注重学生“直观想象”核心素养的发展.
2.渗透“模型化”思想
解立体几何“动态”问题的过程实质是数学建模的过程,正所谓“心中有模型,解题不用慌”.上述可知命题者对圆锥模型“情有独钟”,实际上,只要是几何翻折问题通常都可以借助圆锥模型转化为圆周运动进行研究.当然,在立体几何中,还有其他一些“重要模型”也是值得关注,比如长方体模型,立体几何中的很多概念和定理都是通过长方体模型引入的,很多问题也都可以在长方体模型中找到解决方案.因此,“借几何模型之力,破‘动态’立体几何之困”是非常值得推广的解题策略.当然,只有在平时教学中,不断地渗透模型化思想,学生才能在解题中利用模型,做到游刃有余.
3.强调“动静结合”的辩证思想
一方面,尽管“动态”立体几何题中活跃着动态的点、线、面、体,但在其动态性的层面内、动感化的情境里与变化着的过程中,往往隐藏、蕴含或潜伏着某些不变(静态)的元素与形体.只要细心观察,匠心独运,独具慧眼,善于从动态的图形中捕捉到不变的静态的因素,实现“动中取静,以静制动”之效应;另一方面,充分感知动态的变化过程,仔细观望动态的变化规律,及时捕捉动态的变化轨迹,从而掌握与描绘出其动态变化的一般趋势乃至具体形态,使问题变得有迹可循、清晰可辨,进而实现“动中感知,以动制动”.这就需要教师在教学中要充分体现“动静结合”的辩证思想,使学生掌握“动静转换”的方法与途径,建构“动静合一”的数学思维.
1.马茂年,吴晓明.动态几何 策略引领 理性探索——例说立体几何“动态”题型解题策略[J].中学教研(数学),2014(2).
