思维深度决定视觉宽度

☉江苏省高淳高级中学 田丕丰

思维深度决定视觉宽度

☉江苏省高淳高级中学 田丕丰

（1）求a，b的值；

（2）用x1表示x2；

（3）求证：点M在定直线l上.

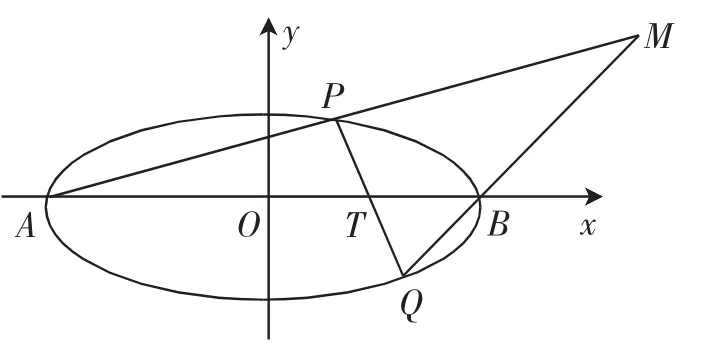
这题是我校2015届高三考前适应性考试的试题，问第（1）问是对有关基础知识的考查，除个别学生外，都能很快得到正确的结果：a=2，b=1，＋y2＝1.第（2）问的设计意图是为解答问第（3）问指明思维方向，降低求解难度.考试后统计表明，能解答第（2）问的学生中，大多数都能完成第（3）问的求解.因此，能否解答第（2）问，是能否完整解答此题的关键点.笔者在阅卷中发现学生对第（2）问求解，出现了四种解法，下面辑录的是这几种解法和笔者的一些浅显的思考.

【解法一】（2）（i）若直线斜率存在时，设直线方程y＝k（x-1），

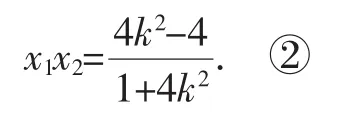
将此式子代入①，化简得5（x1＋x2）-2x1x2＝8，

（ii）若斜率不存在时，x1＝x2＝1，满足上式.

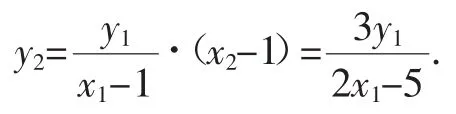
因此，点M在定直线：x=4上.

【评析1】这一解法注意到决定题中各个动点位置的控制变量是直线PQ的斜率k，利用k找到相关动点坐标之间的关系，在本题的设问方式下，学生容易想到消去实数k找出x1，x2的关系，在此基础上解答第（3）问较为顺利.因此，对本题来说，这一解法的思维虽然浅显，却直观有效.但若本题中没有设置第（2）问，用此法时，因为中间目标的缺失，一般学生的思路是用k表示点M的坐标，这样面对很复杂、烦琐的代数式运算，从而导致解题过程无法推进.

以下各种解法，只给出第（2）问的求解过程，第（3）问的解法与上面大致相同，所以省略.

【解法二】设P（x1，y1），Q（x2，y2），M（x0，y0）.若x1≠1，直线PQ方程为代入椭圆方程消去y，得［（x1-1）2＋4y21］x2-8y21x＋4y21-4（x1-1）2＝0，且x21＋4y21＝4，所以（5-2x1）x2-8y21x-5x21＋8x1＝0.由韦达定理得

【评析2】此解法是思考到问题能否获解的关键是设法表示出各个动点的坐标，因而选择动点P的横坐标作为控制变量，直接通过求解方程得到x2与x1的关系，比解法一减少了消参的环节.因此，用此法的学生要比用解法一的学生思维更深一些，而且此法对于在已知曲线联动的两个动点的题型，具有普遍的指导意义.需要提醒的是解题过程中，利用韦达定理可以简化运算.但此法只有学科基础较好、感悟能力较强的学生，经过对相关题型的批量训练才能掌握.

【评析3】此法是利用定比分点的向量形式，找到了关联动点相应坐标的线性关系，再用点差法得动点坐标与参数λ的线性关系，这样消参就很顺利.应该说能想到此法的学生，思维层次较高，综合应用学科知识的意识与能力较好.而且，此法用于处理过定点的动线段两端点相应坐标之间的关系，通常是一种行之有效，运算也不烦琐的好方法.

【解法四】由题知，P（x1，y1），Q（x2，y2），T（1，0），由P，Q，T三点共线得：KPT＝KQT，所以即y（21x2-1）2＝y22（x1-1）2.又有

代入上式得（4-x21）（x2-1）2＝（4-x22）（x1-1）2，

即4（x2-1）2-4（x1-1）2＝x21（x2-1）2-x22（x1-1）2.

由平方差公式整理得5（x1＋x2）-2x1x2＝8，所以x2＝

【评析4】此解法是从多元方程组中通过消元得到部分未知数之间的关系，是实质是从关联动点的运动与变化中，找到相关变量的不变关系.用此法的学生对二次曲线方程的结构特征有较深的研究，能够洞察方程间各类运算的可能结果，对本题中各个条件的代数表示及应用有自己独特的视角，思维广度与深度明显高人一等.不过，此法因其独特，言传效果不佳，只适合于一些有学科特质的学生理解与掌握.

【后记】我们知道：运动与变化、控与被控是解析几何中所蕴涵的最重要的思想方法，而解决这两个问题最基本的数学工具是方程与不等式，因此，数式运算能力的培养是提高解析几何解题能力的基础.上题中几种解法体现，学生解题时的思维深度，决定其解题的视角宽度，也决定了方法的优劣与运算的繁简程度.就教学价值而言，笔者认为前两种解法优于后两种解法.因此，实际教学时，应通过思路分析和解题训练，帮助学生理解和掌握前两种方法.解法一因其思维起点低、入口宽，学生易于理解，是培养学生思维能力必不可少的奠基石.虽然在后续的求解过程中，学生可能因思维偏差和运算能力的欠缺导致解题受挫，同时由于学生有简化运算的心理需求，利于激发学生思维横向拓展和纵向深入的内驱力，优化学生的思维品质.解法二，因其对解题过程相对深入和全方位的思考，且方法具有普遍性指导意义，更具集体教学价值.后两种解法，虽然思维层次很高，但思维切入点隐而难求，且方法的迁移性不强，因而不适合进行以班级为单位的集体教学，可针对部分学科基础好、思维能力强的学生，预先准备好相关题组，在教师指导下自主探究，或许可以取得较好的效果.这是笔者对上题各种解法的一点浅显的思考，不知当否？录此，以博方家一哂.