提高站位,关注高中学生的数学思维培养
2017-01-12江苏省如皋市第二中学沙志峰
☉江苏省如皋市第二中学 沙志峰
提高站位,关注高中学生的数学思维培养
☉江苏省如皋市第二中学 沙志峰
教学质量的优劣与教师的教学意识之间存在着密切的联系,作为教学活动的设计者与主导者,教师对于教学目标的认知,对于最终教学活动的开展起到决定性作用.具体至高中数学教学当中,想要从根本上提升教学实效,强化学生的知识能力,仅仅着眼于零碎的知识内容本身显然是不够的.教师需要做的是提高自己的教学站位,突破具体知识的界限,从思维能力的高度来审视教学活动,进而创新思路,带领学生迈上更高的学习位阶.相比于具体知识内容来讲,数学思维显然是一个更加抽象化、高阶层的内容.虽然看似难以捕捉,但是,它却是决定学生数学学习效果的核心力量.如果能够从思维的高度来把握教学,将会使得整个数学教学过程更加富有实效.
一、创设情境,以兴趣培养思维
思维培养的主体是学生,因此,在这个过程当中,学生的主动融入最为重要.为了让学生对自己的数学思维提升有热情、有渴望,教师需要想办法首先让他们喜欢上思维训练的感觉,这也就是我们所要讨论的以兴趣培养思维.兴趣是思维高效建立的第一驱动力,只要学生对于数学学习产生了兴趣,便会自觉主动地去寻求知识,思维能力自然也就在这个过程当中得到强化了.激发学习兴趣的方法有很多,创设情境就是其中颇为有效的途径之一.
案例1在带领学生学习数列知识时,笔者向大家提出了这样一个问题:小明将一个橡胶球从100米的高度扔下,小球做自由落体运动,每次着地后又回到原来高度的一半后再落下,以此反复.那么,当它第10次着地时,一共经过了多少米?这个颇具实操性的问题,很快将学生带入到了实际生活的情境当中.在这样的真实氛围衬托之下,大家对于这个问题的解决瞬间产生了浓厚的兴趣,也很自然地从中发现了数列的递增规律.
情境的创设正如同为学生知识思维的形成做出了一个前期铺垫,以整体氛围的形式让学生做好接受知识的准备.与此同时,知识情境往往是生动具体的,这也就很好地让知识内容走出了抽象性的限制,以一种真实的面貌展现在学生面前,自然也就更容易被学生所接受和认知.如果这个情境设置得恰当,创设得合理,能够在一开始将学生的关注兴趣激发出来,那么,这种兴趣将会很顺利地延续到思维培养当中,显著提高效率.
二、巧妙设问,以思考培养思维
当然,优质的数学思维也不是凭空产生的,而是需要不断地训练与成长.为了实现对学生思维能力的有效培养,教师应当做些什么呢?笔者认为,最为直接的方式就是运用数学问题来激活思维.既然数学思维是用来解决学习当中所出现的各种问题的,那么,当教师将问题切实摆在学生面前时,自然也就可以将学生的数学思维调动起来.这时候,教师只需要对问题的设计加以调整,就能够巧妙实现思维培养重点的转化,隐教学于无形.
案例2在立体几何的学习中,曾经出现过这样一个问题:如图1所示,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为矩形,PD=DC=4,AD= 2,E为PC中点,求证:AD⊥PC.为了以此为切入点,更好地培养学生的深入思维能力,笔者又在此基础上继续设问:求三棱锥P-ADE的体积.这个问题的难度显然较之前的问题提升了一些.分析完成后,笔者又请学生尝试回答:在线段AC上是否存在一点M,使得PA∥平面EDM,若存在,求出AM的长;若不存在,请说明理由.在这样的渐进式提问当中,学生的思维也随之逐步走向深入了.
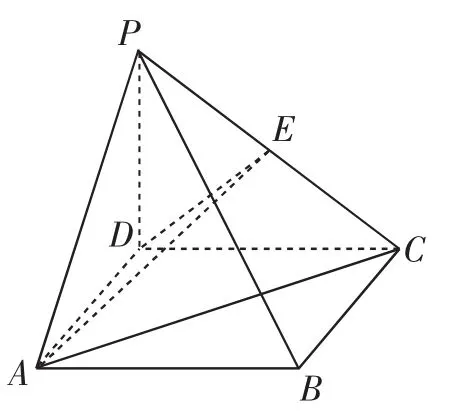
图1
可以说,在数学知识的学习过程中,学生的思维始终是随着自己所面对的问题的变化而变化的.因此,教师便可以抓住这个规律,逆向思维,从设计问题的环节进行把控,进而对学生的数学思维加以影响,实现最终的培养目标.数学知识的学习本就是一个不断提出问题与解决问题的往复过程,对于高中阶段的数学学习来讲,各种形式与内容的富有价值的问题更是层出不穷.如果教师能够将这个资源运用好,并在此基础上巧妙发挥,必然能够设计出有效引领学生思维发展的高质量问题.
三、灵活多变,以创新培养思维
教学方法需要创新,思维培养更需要创新.以传统的途径对学生提出问题或是布置任务,难免会让学生陷入被动思维的困境,对于提高教学实效来讲是十分不利的.为了实现思维培养途径的创新,笔者选择以数学问题的灵活多变为切入点,通过一题多解与一题多变来引发学生的思维多样性变化,且让大家在学习过程中始终不失热情.在高中数学当中,这样的典型性问题有很多,教师只需要从中挑选出最适合当前课堂教学的即可.
案例3在对集合的内容进行教学时,笔者向学生提出了如下问题:已知集合A={1,3,-a3},B={1,a+2},是否存在实数a,使得B⊂A?解答完成后,笔者将问题进行了一些小变化:已知集合A={-1,3,2m-1},B={3,m2},若B⊂A,则实数m的值是什么?在此基础上,笔者又继续将问题进行变式:A={x|x2+x-6=0},B={x|mx+1=0},且A∪B=A,则m的取值范围是什么?随着这样的问题变化,对学生的思维要求显然不断提升了.当学生将最后一个问题顺利解答之后,笔者又将之进行了最后的变化:设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},且A∩B=B,求实数a的值.这个提问将学生本次的思维训练提到了一个小顶峰,也着实深化了大家对于这部分知识内容的理解.
以这种问题变式的途径训练学生的数学思维,对于高中阶段的教学课堂来讲是非常适宜的.高中教学的时间本就紧张,如果教师再去四处找寻不同的数学问题用来开阔学生思维,未免会造成时间与精力过多的浪费.如果能够抓住一个问题加以延伸,以之为基础不断展开变化,学生便无需在解答每个问题时都重新适应条件环境,其思维训练效果也在这个逐步深化的过程中得到加强.对于教师和学生来讲,这都不失为是一种事半功倍的方法.
四、深入挖掘,以探究培养思维
真正全面的数学学习绝不是仅仅涵盖基础知识的学习就够了的,尤其是在高中阶段的学习当中,学生还需要向着知识的深层次再迈进一步,继续进行探究,发现数学内容的完整面貌.与此同时,对当前知识进行深入探究,也是数学思维能力当中必不可少的一个环节.它实现了思维主动性与有效性的整合.
案例4在线面关系的基本内容教学完成后,笔者为学生呈现了这样一个问题,请大家相互探讨:如图2所示,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别为B、D.若增加一个条件就能推出BD⊥EF,现有(1)AC⊥β;(2)AC与α,β所成的角相等;(3)AC与CD在β内的射影在同一条直线上;(4)AC∥EF,能成为增加条件的是哪个?这种提问方式本来就是比较开放的,放在这里正好能够引发学生对于这个问题的探究热情.随着大家的讨论,以及笔者在这个过程中的适当启发,大家关于这类问题解决的思维清晰度与准确度明显提升了.
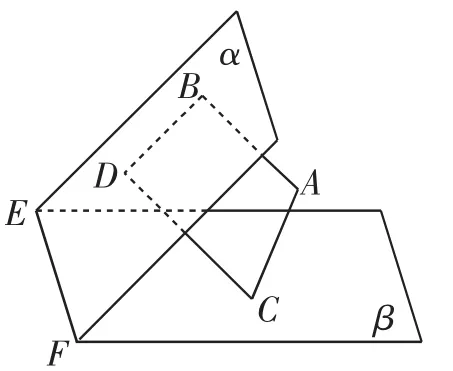
图2
思维训练之初,让学生独立完成探究活动并不是一件容易的事,学生往往会感到开放程度过高,自己的能力无从把握.这时,教师一定要勤于鼓励学生,并适时为之提供启发与引导,参与探究和讨论,让学生逐渐明确这种探究的思维方向.长此以往,当这种意识形成之后,学生的这种思维能力将会得到显著提升,这对于处理复杂问题是很有好处的.
对高中数学知识学习过程进行分析便不难发现,决定学生学习效果的重要因素是思维能力.它就像是一种隐形的动力,推动着学生如何选择学习方式、如何应对复杂问题.可以说,学生的思维模式直接影响着他们对于数学内容的理解和处理效果.放眼高中数学领域,各种类型的问题层出不穷,其所对应的思维方式也是各不相同的.因此,教师在设计教学活动时,要从不同的角度着手,对学生的思维能力进行培养,让大家在多样化的数学课堂中实现数学思维的全面发展.找准了这个站位,就像是将高中数学课堂提升了一个位阶,让我们得以在更为广阔的视角下优化教学,强化效果.
1.周频.浅析高中数学生成性课堂的构建策略[J].教育导刊,2012(6).
2.徐金光.高中数学生成性课堂的构建策略分析[J].新课程研究(下旬刊),2013(9).
