基于混合粒子群算法的白车身焊接机器人路径优化

周红勋，陈君宝，王生怀，陈育荣

（湖北汽车工业学院 机械工程学院，湖北 十堰 4420002）

基于混合粒子群算法的白车身焊接机器人路径优化

周红勋，陈君宝，王生怀，陈育荣

（湖北汽车工业学院 机械工程学院，湖北 十堰 4420002）

提出了一种由粒子群算法和遗传算法有效结合的混合粒子群算法。以某型轿车前地板线焊接工位机器人的路径规划为例，分别采用混合粒子群算法、遗传算法对机器人的焊点焊接顺序进行求解。2种算法在Matlab中的仿真优化结果表明：混合粒子群算法在求解路径优化问题上能得到更佳的焊接路径。

白车身；焊接机器人；混合粒子群算法；路径优化

白车身作为汽车的重要组成部分，通常由300～500个形状复杂的薄板冲压件组成，需要在55～75个工位上焊接4 000～6 000个点［1］。为了能在较短的时间内制造出高质量、低成本的车身，满足市场的需求和提高市场占有率，国内外企业纷纷采用以机器人为核心的柔性焊装生产线。为了使机器人在尽可能短的时间里，无干涉地完成焊接任务，必须对焊接任务进行分配、每台机器人焊接路径进行优化。由于本文中以某型轿车前地板线补焊工位为研究对象，焊点分配任务已完成，故此处只需考虑焊接路径的优化。以往机器人的路径规划常常由人工完成，仿真人员主要根据自己的经验以及已有的资料，粗略规划出机器人焊点焊接顺序，这种规划方法具有很大的随意性，并且效率低，经常出现机器人作业顺序不合理，从而严重影响白车身焊接的生产效率［2］。为此，近年来国内外许多研究者采用诸如遗传算法、神经网络等智能算法来研究机器人的路径优化问题，虽然在解决路径优化方面有了很大的提高，但由于这些智能算法本身的不足，往往产生诸如寻优效果不理想等不足。为了得到更好的优化结果，本文中在对遗传算法和粒子群算法的研究上，提出一种融合了上述2种算法各自优点的智能算法——混合粒子群算法，并将其用于优化某型轿车前地板线补焊工位的机器人焊接路径优化上，对于缩短焊接时间、提高生产效率、节约成本具有十分重要的意义［3］。

1 白车身焊接路径优化模型的建立

以轿车前地板线工位焊接上一台焊接机器人的路径优化为研究对象，需要焊接28个焊点，在地板上的分布如图1所示。由于其焊点分布范围广、不规则，从而增加了机器人运动时间和路径，成为了阻碍整个焊接系统效率的瓶颈。机器人路径优化就是找一条最优或者次优的焊接路径，使机器人的工具原点从起始点开始，依次焊接完28个焊点，又回到起始点，所用的时间或路程最短，因此焊接路径问题是典型的旅行商问题。由于智能算法是从理论上对机器人路径进行优化，得到的结果往往需要现场修正，为了提高计算效率，最大限度地模仿真实环境，可以作如下简化：1）焊接过程中焊枪和工件或夹具干涉问题，这方面可以用增加虚焊点修正的方法加以解决［4］；2）不考虑焊接变形等约束条件对焊接顺序的影响；3）通过对图中28个焊点的坐标进行分析可知，它们在Z轴上的偏差十分小，故在优化时不考虑Z轴的变化，直接把焊点看成在XOY平面上的点。

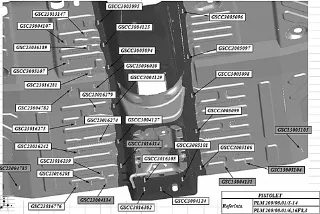
图1 地板线焊点分布图

为了简化模型，以机器人的焊接路径最短为规划目标，设C={C1,C2,C3,…,C28}为28个焊点的全排列，d（Ci，Ci+1）为非负数，表示排列顺序为Ci和Ci+1焊点间的距离，s为焊接路径总长度，求使目标函数式（1）路径长度达到最小的28个焊点的顺序排列：

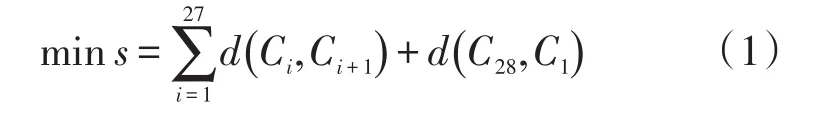
2 遗传算法和粒子群算法

2.1 遗传算法

遗传算法是美国密歇根大学John H.Holland教授提出的一种随机自适应的全局搜索算法，其基本原理是仿效生物界中的“物竟天择、适者生存”的演化法则［5］。在用于解决机器人路径规划的旅行商问题时，将所有焊点焊接顺序表示成染色体。随后在可行解空间中初始化若干条染色体，根据适应度值函数计算种群中每条染色体的适应度值，选择其中适应度值高的染色体，对它们依次进行交叉，变异操作，产生更好的染色体种群。这一过程反复循环，当达到设定的最大遗传代数时，算法结束，输出最优解，此算法的流程图如图2所示。

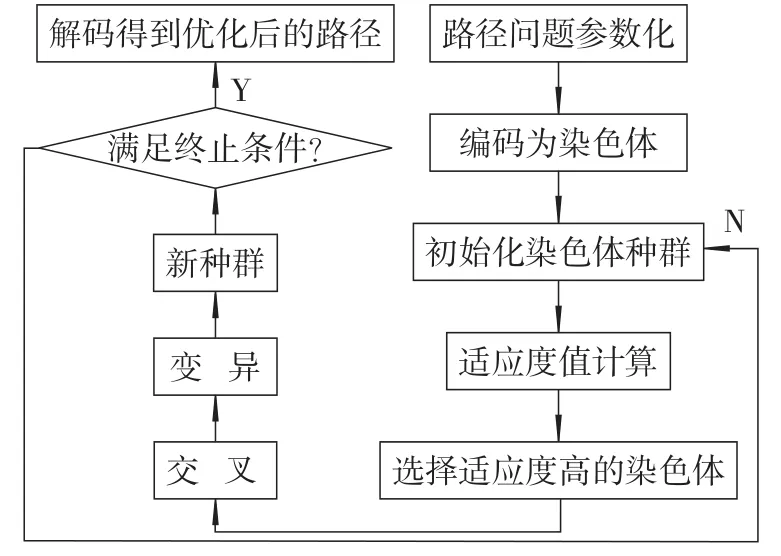
图2 遗传算法流程图

2.2 粒子群算法

粒子群算法则源于鸟类捕食这种生物种群行为的启发而提出一种基于群体智能的全局随机搜索算法，用可看成质点并且以一定速度飞行的粒子表示个体。假设在D维搜索空间中有N个粒子，Xi=（xi1，xi2，…，xiD），Vi=（vi1，vi2，…，viD）分别表示第i（i=1，2，3，n）个粒子的位置和速度，通过不断追踪粒子个体极值Pbest=（pi1，pi2，…，piD）（个体经历过的最好位置）和种群极值Gbest=（pg1，pg2，…，pgD）（种群中所有个体经历过的最好位置）来更新个体的位置和速度，更新公式为

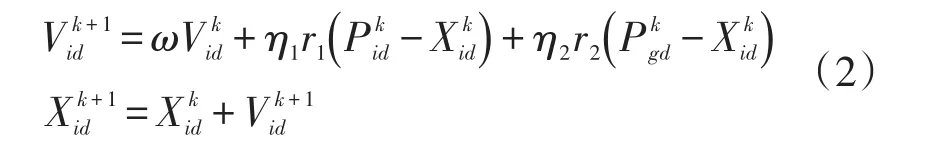
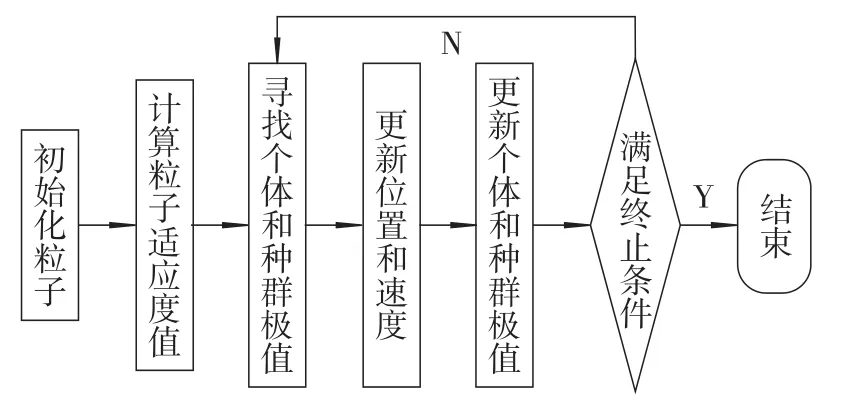
图3 粒子群算法流程图

3 混合粒子群算法路径优化过程

遗传算法采用选择、交叉和变异算子进行搜索，全局搜索能力较强，能有效解决离散优化组合问题，但局部搜索能力较弱，很难得到问题的最优解。而基本粒子群算法通过追随个体极值和种群极值完成极值寻优，在解决非线性连续性的优化问题上操作简单、收敛迅速、寻优能力强，但随着迭代次数的不断增加，易陷入局部最优解周边和无法用于离散的优化组合问题（不能用于焊接机器人的路径规划问题）等。为了弥补它们在求解路径优化问题上的不足，本文中提出了一种由粒子群算法和遗传算法有效结合的混合粒子群算法，它结合2种算法各自的优点，避免了各自的不足，摒弃了传统粒子群算法中的通过极值来更新粒子位置的方法，而是通过粒子同个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解，从而增加种群的多样性，提高算法的全局搜索能力［6］。

3.1 求解过程

1）个体编码 混合粒子群算法采用整数编码的方式，即用一组所有焊点的焊接顺序排列表示粒子、所有焊点的全排列当成搜索空间的这种表达方式。比如当有10个焊点，个体编码为（4 1 9 2 3 7 6 8 5 10），表示焊接顺序从4开始，经过1，9，2……10，最终返回焊点4，从而完成焊接任务。

2）适应度函数的设计 适应度值表示为机器人焊接完所有焊点所运动的路程，如式（3）所示：

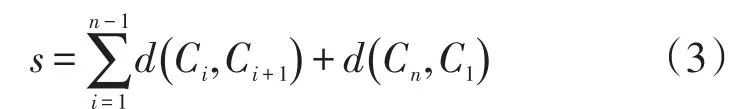
式中：n为焊点个数；d(Ci,Ci+1)指粒子中排列顺序为(Ci,Ci+1)的2个焊点之间的距离。

3）交叉算子的设计 基本粒子群算法无法用于离散的机器人焊点路径优化，故混合粒子群算法通过和个体极值、种群极值交叉来更新个体，采用整数交叉的方法。首先选择2个交叉位置，然后把个体和个体极值、种群极值进行交叉。假定随机选取的交叉位置为2和7，个体（4 1 9 2 3 7 6 8 5 10）与极值（9 2 1 6 3 7 4 10 8 5）交叉得到新个体（9 1 1 6 3 7 6 10 8 5）。假如产生的新个体存在重复位置，则用个体中未包括的焊点代替重复包括的焊点，将新个体（9 1 1 6 3 7 6 10 8 5）调整为（9 4 1 6 3 7 2 10 8 5）。如果交叉后新个体适应度值变小，则用它代替原个体，否则原个体保持不变。

4）变异算子设计 为改善新算法的局部搜索能力，挖掘个体粒子的多样性，混合算法在交叉算子后面增加了变异操作，采用个体内部2位互换方法，首先随机选择变异位置互换，假设选择的变异位置为5和9，变异操作如（9 4 1 6 3 7 2 10 8 5）变异成（9 4 1 6 8 7 2 10 3 5）。如果变异后个体适应度值变小，则更新原个体，否则原个体保持不变。

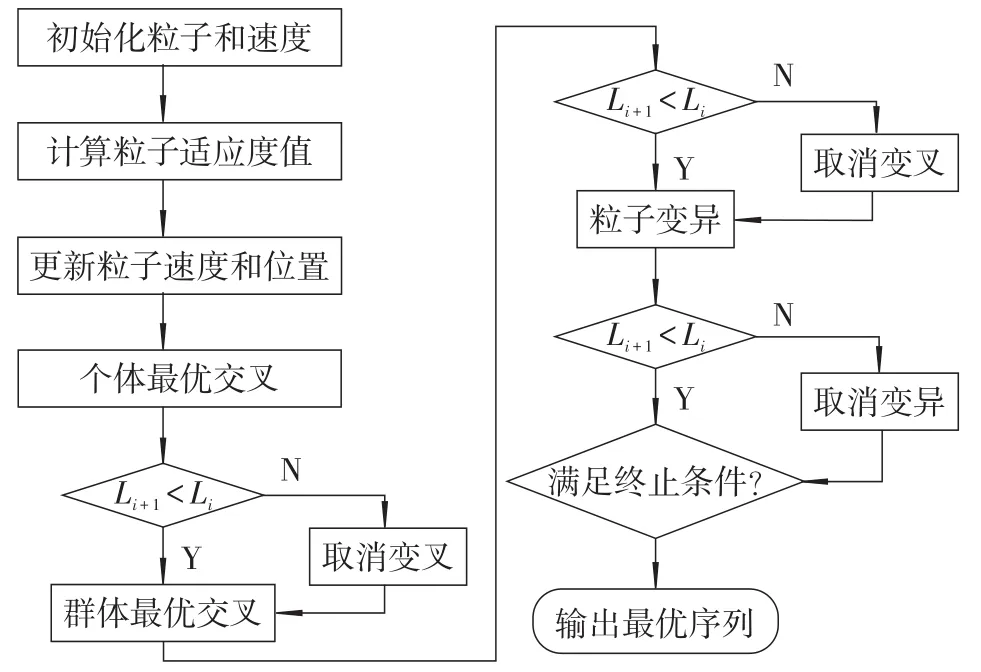
图4 混合粒子群算法流程图

3.2 算法流程

混合粒子群算法流程图如图4所示。具体步骤为：1）初始化种群中粒子的随机位置和个体数目。2）适应度值计算。计算粒子群个体的适应度值即焊接完所有焊点所运动的总路径长度。总路径长度越小的粒子对应的适应度值越大，粒子越优秀。3）更新粒子。根据粒子适应度值更新个体最优粒子和群体最优粒子。4）个体最优交叉。把个体和个体最优粒子进行交叉得到新粒子，如果新粒子的适应变大，则接受变异，否则不接受变异。5）群体最优交叉。把个体同群体最优粒子进行交叉得到新粒子，如果新粒子的适应变大，则接受变异，否则不接受变异。6）变异操作。对所得到的新个体采用保留优秀个体策略，变异之后适应度变大则接受变异，否则不接受。7）达到最大迭代次数程序结束，输出结果；否则，返回步骤2），继续执行。

4 规划及仿真结果分析

在Matlab中分别编写优化机器人焊接路径的遗传算法程序和混合粒子群算法程序。遗传算法中迭代次数取500次，种群大小取1000，交叉概率取0.9，变异概率取0.05；混合粒子群算法程序中迭代次数取500次，种群大小取1000，惯性常数随着迭代次数的增加，由0.9线性递减到0.4，取加速度因子η1和η2均为2，共有28个焊点，如图5所示。

由于上述2种算法都为随机搜索算法，不可能每次运行得到的结果都一样，为了保证算法的可比较性，将每种算法分别运行20次，取平均值，并且分别取里面适应度值最小的那组仿真结果作为各自最终路径优化的结果，如表1所示。

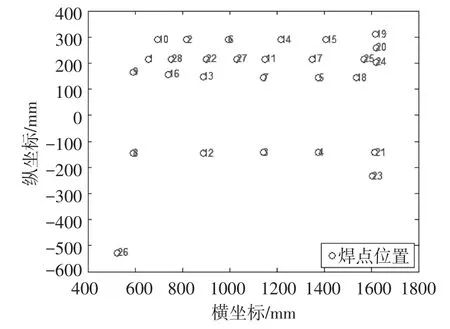
图5 焊点平面分布图

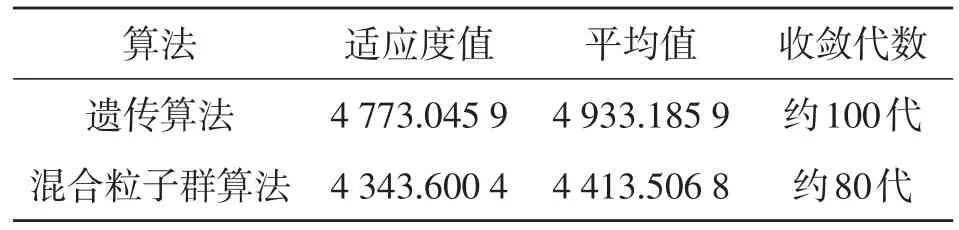
表1 不同算法在路径优化中的结果对比

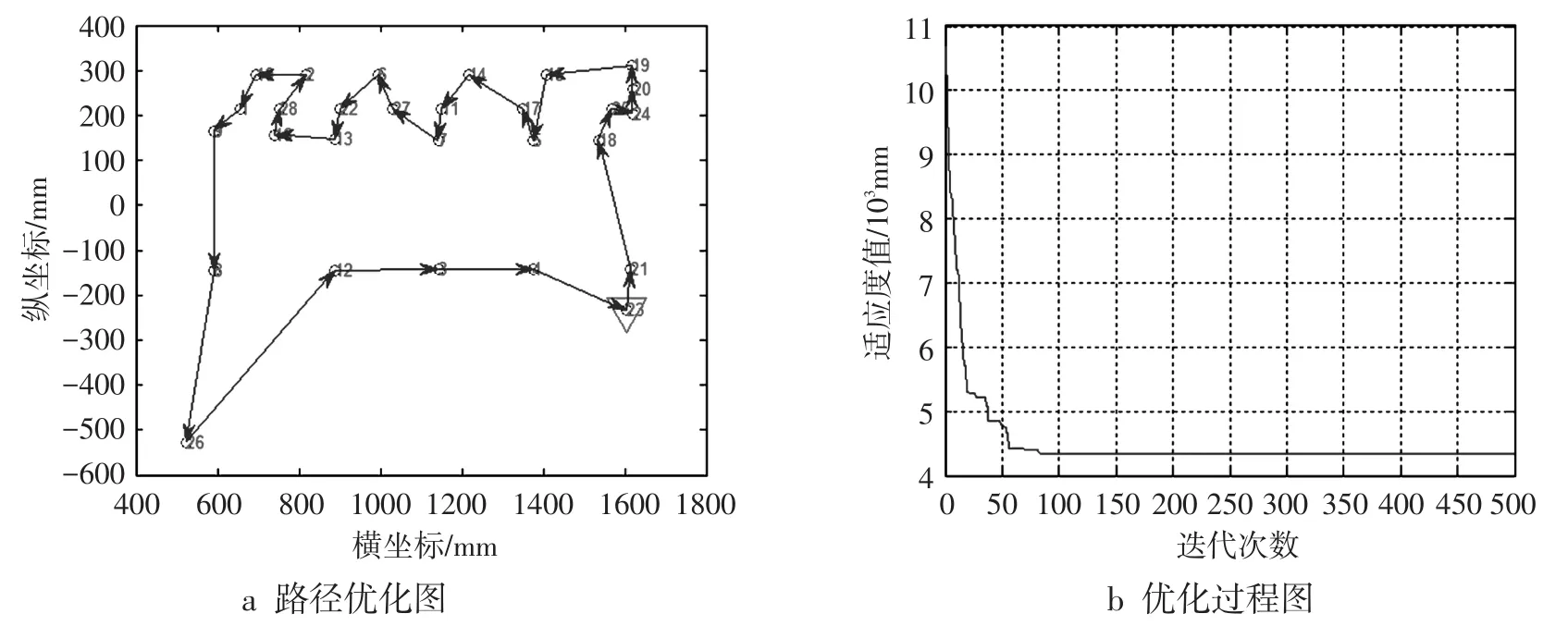
图6 混合粒子算法路径优化和优化过程图

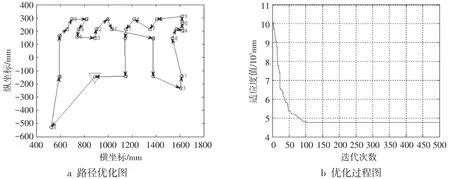
图7 遗传算法路径优化和优化过程图

混合粒子群算法优化的路径及适应度值如图6所示，由图6 b可知：算法进化到80代左右，适应度值达到最小并不再变化，得到全局最优解，焊接最优顺序如图6 a所示（从焊点23开始沿着箭头顺序焊接），总路程为4343.6004mm。遗传粒子群算法优化的路径及适应度值如图7所示，由图7b可知：算法进化到100代左右，适应度值趋于稳定，最优路径如图7 a所示（从焊点12沿着箭头顺序焊接），总路程为4773.0459mm。

由仿真分析可知：混合粒子群算法在解决机器人路径优化问题上，克服了遗传算法收敛慢，寻优能力不强等不足，优化所得到的最优路径和时间比遗传算法的更短，提高了优化效率。

5 结语

本文中提出一种解决机器人路径优化旅行商问题的智能算法——混合粒子群算法，它引入遗传算法中交叉和变异操作，通过粒子与个体极值和种群极值的交叉以及粒子自身变异的方式来搜索最优解。将遗传算法和混合粒子群算法分别用于求解前地板线补焊工位上机器人的焊接路径，并在Matlab上仿真。仿真结果表明：混合粒子群算法比遗传算法在优化机器人焊接路径上有更大的优势，得到的焊接路径更好，速度更快。由于混合粒子群算法具有更好的全局搜索能力和收敛效果，故其在缩短机器人焊接时间、提高生产率、节约成本方面取得的效果更明显。

［1］晁永生，刘江海.白车身焊接机器人加工路径优化和仿真［J］.中国机械工程，2010，21（4）：442-445.

［2］赵硕.多机器人协同的焊接路径规划研究［D］.合肥：合肥工业大学，2015．

［3］宋林森，杜紫薇，郭好杰.汽车白车身焊接机器人焊接路径优化技术研究［J］.制造业自动化，2011，33（9）：63-67.

［4］王学武，时应盼.基于分区粒子群算法的焊接机器人路径规划［J］.华东理工大学学报，2011（4）：639-645．

［5］朱莹莹，王宇嘉.求解复杂旅行商问题的混合粒子群算法［J］.轻工机械，2015（4）：43-43．

［6］郁磊，史峰，王辉.MATLAB智能算法［M］.北京：北京航空航天大学出版社，2015：144-145．

Path Optimization of Body-in-white Welding Robot Based on Hybrid PSO Algorithm

Zhou Hongxun,Chen Junbao,Wang Shenghuai,Chen Yurong
（School of Mechanical Engineering,Hubei University of Automotive Technology,Shiyan 442002,China）

A new hybrid particle swarm intelligence algorithm was presented based on the particle swarm optimization（PSO）algorithm and genetic algorithm.Taking the welding station robot path plan⁃ning of the first floor line for a car as an example,the hybrid particle swarm optimization algorithm and genetic algorithm were respectively adopted to solve for the solder welding sequence.The simulation op⁃timization results of the two algorithms in Matlab show that the hybrid PSO algorithm is more effective to solve the problem of the welding robot path optimization.

body-in-white;welding robot;hybrid PSO algorithm;path optimization

TP301.6

：A

：1008-5483（2016）04-0043-04

10.3969/j.issn.1008-5483.2016.04.010

2016-07-11

国家自然科学基金项目（51275159，51475150）；湖北省自然科学基金项目（2013CFB045）；

湖北省教育厅科学技术研究重点项目（D20141802）

周红勋（1986-），男，湖北黄冈人，硕士生，从事白车身焊接机器人路径优化研究。E-mail：1069706661@qq.com