RC框架核心筒结构的地震易损性研究

郑山锁， 张艺欣， 秦 卿， 杨 威， 甘传磊， 左 英

(西安建筑科技大学 土木工程学院，西安 710055)

RC框架核心筒结构的地震易损性研究

郑山锁， 张艺欣， 秦 卿， 杨 威， 甘传磊， 左 英

(西安建筑科技大学 土木工程学院，西安 710055)

为研究高层RC框架核心筒结构的地震易损性，设计9榀相同层高但不同跨度和地震设防烈度的典型结构模型。考虑地震动输入的不确定性，采用Perform-3D对其进行弹塑性动力时程分析得到结构地震响应，进而结合我国抗震规范对框架核心筒结构体系性能水平限值要求建立相应的地震易损性曲线，对比分析了不同跨度和设防烈度下结构的地震易损性差异;结果表明：较低设防烈度结构的地震易损性曲线差别不明显，而较高抗震设防烈度下结构的地震易损性曲线差别显著；在相同设防烈度下，随着结构跨度的增加其地震易损性曲线变化不大，从一个方面验证了结构设计的不确定性对其地震易损性的影响较小。研究为进行城市高层建筑结构的地震灾害损失评估提供了理论依据。

高层RC框架核心筒结构；易损性曲线；地震动输入；结构设计

地震风险分析包括地震危险性、地震易损性和地震损失，其中地震易损性，是新一代基于性能的地震工程主要研究目标。结构地震易损性是指结构在不同强度地震作用下，结构达到某一极限状态的概率[1]，可表示为概率地震需求模型和概率抗震能力模型的卷积[2]。城市中的高层建筑作为缓解土地资源的有效手段日益成为结构设计的主流，其中的框架核心筒体系因同时具有建筑功能适用性强和良好的抗侧刚度，应用十分广泛。目前对该类结构的地震易损性研究较少，主要有：何益斌等[3]对不同节点连接方式的高层钢框架-混凝土核心筒结构进行地震易损性分析；刘阳冰等[4]对高层组合结构进行地震易损性研究，同时分析了框架梁柱截面、核心筒厚度和楼层数对该类结构地震反应的影响；YANG等[5]对美国旧金山地区一栋42层RC(Reinforce Concrete)框架核心筒结构进行了地震易损性分析和损失评估等。

为了得到能反映实际钢筋混凝土框架核心筒结构的一般易损性曲线，需要建立典型原型结构，并且考虑结构能力不确定性和地震动需求不确定性。对于这些不确定性的考虑方法主要为蒙特卡洛模拟法，但是这对于高层结构动力时程分析过于耗时，故本文仅考虑其中主要的影响因素。KWON等[6]提出材料特性的不确定性与地震动不确定性相比较小；PORTER等[7]研究发现包括质量和阻尼在内的结构不确定性对易损性的影响较地震动不确定性较小。基于上述结论，本文选取了不同设防烈度和不同跨度的结构进行地震易损性分析。其中，抗震设防烈度是对结构进行抗震设计和采取抗震构造措施的依据；跨度是结构不确定性的主要因素，决定结构的高宽比，是对结构刚度、整体稳定、承载能力和经济合理性的宏观控制[8]。鉴于此，本文共设计9榀框架核心筒结构模型，并考虑地震动不确定性建立概率地震需求模型，参考我国现行抗震规范定义结构概率抗震能力，进而获取易损性曲线，揭示跨度和设防烈度的影响。

1 原型结构设计

1.1 设计参数

结构的平立面布置以一般性和代表性为原则，采用双向现浇钢筋混凝土框架结构，平面布置见图1[9]，结构共30层，总高度98.7 m，立面层高变化见表1。跨度分别取为6 m、8 m、10 m，与设防烈度6，7，8度相结合(考虑规范对该类结构最大高宽比和适用高度的限制)，共设计了9个模型。为方便叙述，对不同结构模型进行编号(见表2)。

表1 立面层高变化

Tab.1 Storey height

层数1～789～30层高/mm420033003000

图1 结构平面布置图Fig.1 Layout of structures

表2 模型编号

为保证分析结果相对真实，根据我国现行设计规范，以多遇地震下最大弹性层间位移角为控制指标，采用国内通用设计软件PKPM分别对上述9个结构进行设计，结构共同设计资料包括：场地类别Ⅱ类，地震分组第一组；基本风压0.385 kN/mm2，地面粗糙度为C类。梁柱墙主筋采用HRB400，箍筋采用HRB335；各楼(屋)面板重力荷载标准值见表3，其余设计参数见表4(同层剪力墙及柱混凝土强度与梁相同)。

表3 各楼(屋)面板重力荷载标准值

Tab.3 Standard values of gravity load

楼层2～78～3031恒载/(kN·m-2)53.55.5活载/(kN·m-2)3.51.52

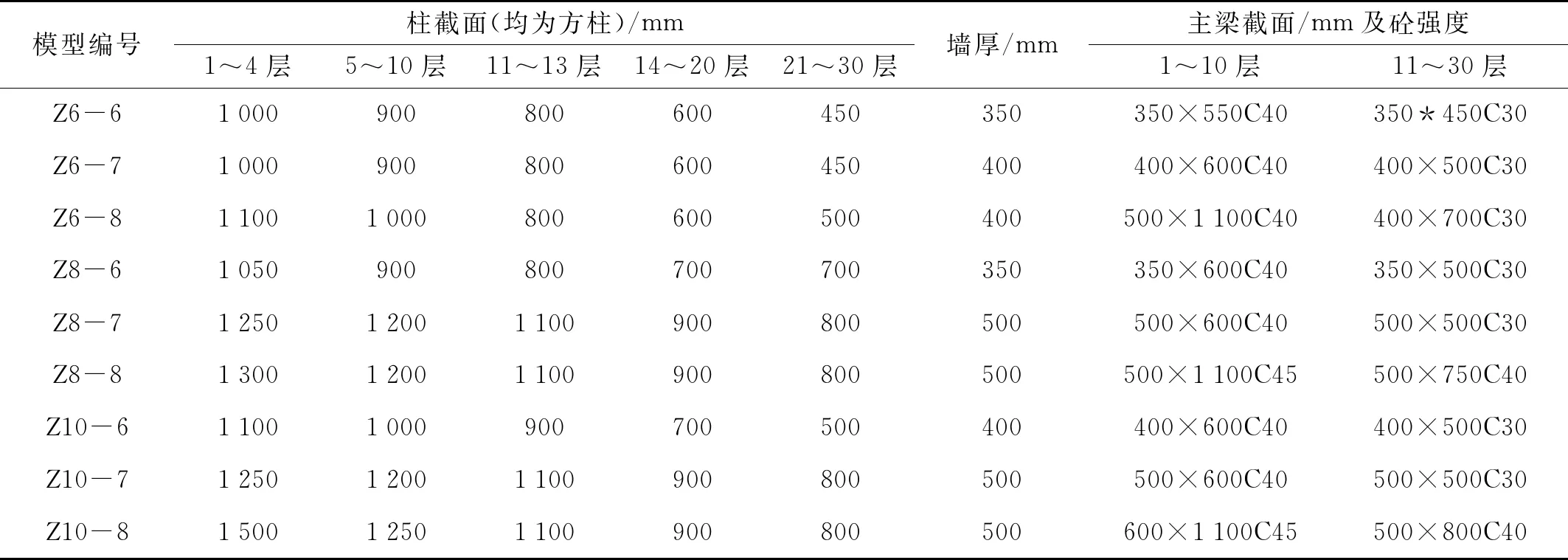
表4 主要结构构件截面参数及混凝土强度

1.2 有限元分析模型

考虑到高层结构的计算效率，本文选择三维非线性分析软件Perform-3D作为有限元分析平台。为验证结构弹性模型的正确性，进行模态分析，与PKPM软件中的结构周期和质量对比。原模型的结构总质量为31 898.5 t，分析模型为32 033 t，误差仅为0.42%，周期对比具体数值见表5。从表5可知，校校核结果比较接近，说明弹性模型信息基本一致。

表5 模型周期对比

进行动力时程分析时，梁采用Perform-3d中塑性铰单元中的弯矩曲率铰模拟，当跨高比超过2.5时设置剪切铰以考虑剪切特性。由于纤维模型可以同时考虑轴力以及双向弯矩的影响，故柱、墙采用纤维单元。为近似考虑楼板对整体结构受力的影响，设置刚性楼板。

2 概率地震需求分析

结构的概率地震需求分析即建立地震动强度与结构反应的关系。通过选取22条地震动记录并进行调幅，对结构进行动力时程分析得到地震响应，从而建立概率地震需求模型。

2.1 地震动记录的选取

地震动的不确定性包括峰值、频谱特性和持时等因素，需要通过输入大量的地震动记录予以考虑，这里采用美国应用技术委员会在ATC-63(2008)报告[10]中建议的八项选取原则并选用ATC-63报告给出的22条远场地震动记录(见表6)。

表6 本文选用的22条远场地震动记录

2.2 地震动强度指标和结构响应指标的选取

在结构易损性曲线的建立中，选取合适的地震动强度指标(IM)和结构响应指标尤为关键。合理的地震动强度指标不仅需要反映地震动的特性如幅值，还应反映结构的响应指标，现有IM指标包括地面峰值加速度(PGA)、地面峰值速度(PGV)、第一周期谱加速度 (Sa)、累积绝对速度(CAV)等。研究结果表明，其中Sa与传统的PGA指标相比可降低结果离散型[11]，且与结构的周期有关，故选用Sa作为IM指标。

结构响应指标用于表征结构在地震作用下的动力响应，在概率能力分析中即结构的损伤指标DM(Damage Measure)，而对应于概率需求分析即工程需求参数EDP(Engineering Demand Parameter)。在确定的地震动强度指标下，合理的结构响应指标可以使结果的偏差减小，更准确地评估结构抗震性能。常用的指标主要包括：结构顶点位移、最大层间位移角、楼层最大延性比、基底剪力等。其中最大层间位移角可与我国现行抗震规范相结合，且应用较为广泛，故本文将其作为结构响应指标。

2.3 概率地震需求模型

通常可以认为地震动强度指标IM与结构工程需求参数EDP之间的关系满足下列公式：

EDP=α(IM)β

(1)

假设工程需求参数的中位值mD/IM与地震动强度指标IM服从指数关系：

mD/IM=α(IM)β

(2)

对上式两边同时取对数得

lnmD/IM=a+bln(IM)

(3)

式中:a=lnα、b=β。根据式(3)，通过时程分析结果Di(i=1,2,…,N)进行对数线性拟合，可获得对数标准差为：

(4)

式中:N为回归分析的数据点个数。

将每条地震波的反应谱加速度Sa在结构基本周期(T1)分别调整为0.05 g、0.1 g、0.2 g、0.3 g、0.4 g、0.5 g[12]， 该范围可基本覆盖各个结构从弹性阶段进入弹塑性阶段直至倒塌。图2为各地震波加速度反应谱及均值反应谱。

图2 22条地震波弹性反应谱

对每个结构输入调幅后的地震波，进行弹塑性动力时程分析，可以得到对应于不同谱加速度的结构最大层间位移角，以跨度为8 m分别在7度设防和8度设防的结构为例，数据如图3所示，能够看到不同抗震设防烈度下的结构地震需求差异较大。对横纵坐标分别取对数后绘于坐标图中，并对数据点进行线性回归分析，即可得到以lnSa为变量的需求概率模型。

由图4可知，回归得到的概率需求模型为：

lnθmax=0.999 8lnSa-3.002 0 (模型Z6-7) (5)

lnθmax=0.986 0lnSa-3.530 6 (模型Z6-8) (6)

图3 最大层间位移角与Sa的关系

图4 各模型的线性回归分析

3 地震易损性分析

3.1 方法综述

结构的地震易损性表示在不同强度地震作用下，结构需求超过特定破坏状态的概率。现有研究资料多根据CORNELL等[13]提出的地震易损性求解过程，现详细介绍此求解过程：

地震易损性函数F(x)的一般表达式为：

(7)

式中:Φ[·]为标准正态概率分布函数；m为地震易损性函数的中位值；β为地震易损性函数的对数标准差。

采用式(7)的形式，改写为

(8)

(1)a、b和βD/IM已在概率地震需求分析求得，具体数值见表7；

(2) mC和βC为结构极限状态抗震能力的中位值和对数标准差，可采用下式计算获得：

(9)式中:μC和δC为不同极限状态的能力平均值和变异系数。根据规范参考控制目标位移，选取结构极限状态抗震能力的中位值mC；βC依据HAZUS(FEMA2003)[14]，取为0.25(现行规范设计)。

3.2 结构性能水平划分

结构性能水平的定义与地震易损性曲线状态位置直接相关，也是对结构抗震性能作出正确评估重要的一环。针对所选的结构工程需求参数即最大层间位移角，采用我国规范建议的判断准则[15]，对结构的破坏状态分为完好、轻微破坏、中等破坏、不严重破坏和严重破坏，即需要确定四个阀值，达到轻微破坏状态时构件处于开裂状态，大致取中等破坏的1/2，中等破坏大致取到规范弹性限值和弹塑性限值的平均值，当构件接近极限承载力时变形比中等破坏小些，不严重破坏大致取到规范不倒塌的弹塑性变形限值的90%，具体数值见表8。根据《建(构)筑物地震破坏等级划分》:GB 24335—2009-T对钢筋混凝土框架核心筒结构破坏状态的描述，，中等破坏状态为多数框架梁、柱构件或剪力墙出现轻微裂缝，部分出现明显裂缝，个别梁、柱或剪力墙端部混凝土剥落；严重破坏为多数框架梁、柱构件或剪力墙出现明显裂缝，个别出现了严重裂缝，裂缝周围大面积混凝土剥落，部分墙体主筋屈曲。

表8 层间位移角量化指标限值

3.3 抗震设防烈度对地震易损性曲线的影响

抗震设防烈度是一个地区作为抗震设防依据的地震烈度，直接影响结构的设计地震力与抗震构造措施。分别给出不同设防烈度下的结构(以6 m和8 m跨度为例)超越四种性能水平限值的地震易损性曲线，见图6、图7。

从图6、图7可知，随着抗震设防烈度的提高，结构的地震易损性曲线趋向平缓，即超越固定性能水平的概率减小，抗震能力提高。同时，6度及7度抗震设防结构的地震易损性曲线较为接近，而与8度结构的地震易损性曲线差距较大。这说明在6度抗震设防的条件下，虽然设计地震力很小，对于配筋的影响不大，但是抗震构造要求仍然使结构具有良好的抗震性能。

同时，从完好发展到不严重破坏状态，不同设防烈度结构的地震易损性曲线差距变大，即这些结构从超越完好状态到超越轻微损坏状态的概率相当，而抵抗中等破坏和严重破坏的能力差距较大，结合结构延性的定义，即在保持结构的基本承载能力的情况下极限变形和屈服变形的比值，则随着设防烈度的提高，体型相近的结构延性也随之增大。

最后，在结构第一周期对应的谱加速度Sa较小时，曲线基本重合，随着Sa的增大，曲线差距逐渐明显，而在Sa进一步增大时曲线又有合拢的趋势。这是因为在结构的弹性阶段，设防烈度的提高对结构抗震性能的影响并未得到体现，而随着结构进入弹塑性阶段，设防烈度提高显著提升了结构的抗震性能，当结构趋于破坏时，这种影响减弱。

3.4 跨度对易损性曲线的影响

为进一步研究在相同抗震设防的情况下，对结构易损性影响较大的因素，分别做出抗震设防烈度相同而跨度不同的结构在各个性能水平下的易损性曲线，见图8、图9。

图6 不同设防烈度结构的地震易损性曲线(跨度为6 m)

图7 不同设防烈度结构的地震易损性曲线(跨度为8 m)

对比图9所给的易损性曲线，可知：

(1)在两种抗震设防烈度下，曲线均随着跨度的增大而变得平缓，表明结构达到四种性能水准的概率减小，即结构的高宽比减小，有利于结构的抗震。

(2)相同设防烈度不同跨度结构的地震易损性曲线比较接近，而且在8度抗震设防烈度下表现更加明显。从设计的角度分析其原因：7度抗震设防下跨度分别为6 m、8 m和10 m的结构，在小震作用下弹性层间位移角分别为1/1 066、1/1 092和1/1 339，8度下分别为1/968、1/986和1/1 070，可以看出，在同一抗震设防烈度下，弹性层间位移角相近的结构，其易损性也相近，即弹性层间位移角作为抗震变形验算的指标，能够从一定程度上反映结构进入非线性阶段后的弹塑性层间位移角；同时也说明按照现行规范所设计的结构，跨度对易损性的影响并不显著，为进一步确定跨度与结构易损性的关系，可通过分析跨度与易损性参数的相关性得到，具体数据如表8。从表8中可知，跨度与易损性参数为弱相关或无相关，不能简单地认为随着结构高宽比的增大，抗震性能减弱。这也从一定程度上反映了结构设计的不确定性对地震易损性影响较小。

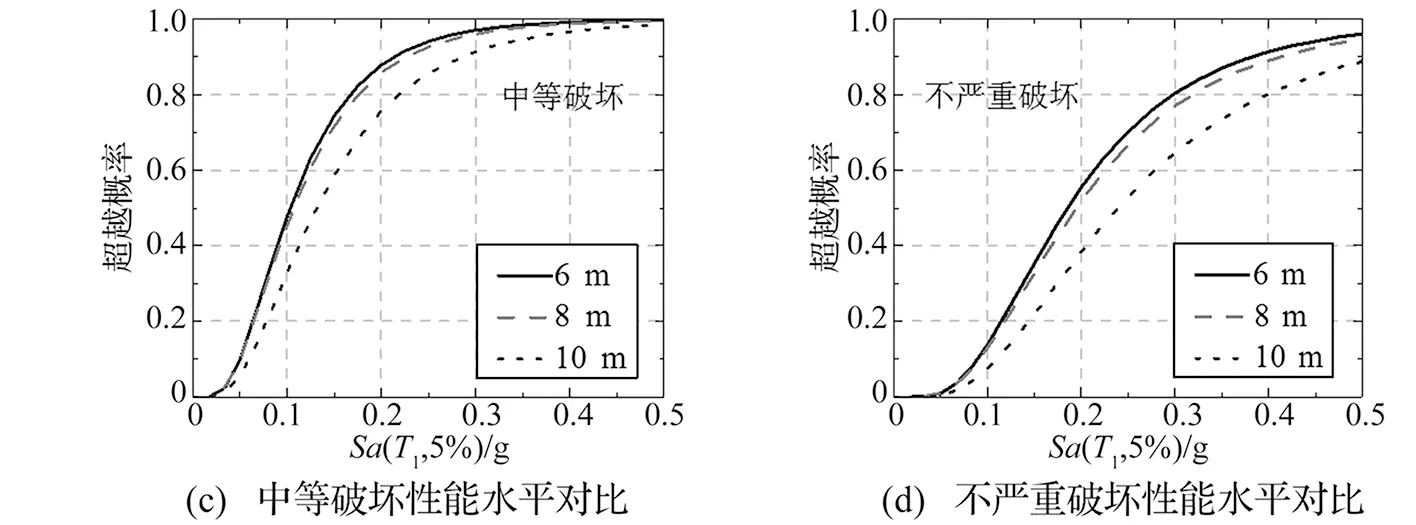
图8 不同跨度结构地震易损性曲线(抗震设防烈度为7度(0.1 g))

图9 不同跨度结构地震易损性曲线(抗震设防烈度为8度(0.2 g))Fig.9 Seismic fragility curves of different span structures (fortification intensity is 8(0.2 g) degree)

表8 跨度与易损性曲线参数相关系数

3.5 框架核心筒结构地震易损性曲线的建立

由上述分析，将相同烈度下不同高宽比结构的易损性数据重新拟合可建立该类结构的地震易损性曲线(见图10)，图中虚线为该设防烈度下不同跨度结构的地震易损性曲线，实线为该设防烈度下结构的平均地震易损性曲线。

由图10可知，在轻微破坏状态下结构地震易损性曲线离散较小，在不严重破坏下离散程度较大；6度与7度设防下结构地震易损性曲线近似相同，而与8度差距较大，这与上述设防烈度对易损性曲线的影响一致。总体上，各个设防烈度下结构的平均地震易损性曲线与不同跨度结构的地震易损性曲线差距较小，可基本代表在一定设防烈度下该类结构的地震易损性曲线，该结论为建立城市高层建筑结构的地震灾害损失评估系统提供了理论依据。

图10 不同抗震设防烈度设计的结构地震易损性曲线

4 结 论

(1)7度(0.1 g)设防及以上的情况下，抗震设防烈度是影响高层RC框架核心筒结构抗震能力的重要因素；6度设防和7度(0.1 g)设防的结构地震反应相近。

(2)高宽比对结构的易损性曲线有一定的影响，但影响并不显著，从一个方面验证了结构设计的不确定性对地震易损性影响较小。

(3)各个设防烈度下高层RC框架核心筒结构的平均地震易损性曲线与不同跨度结构的地震易损性曲线差距较小，可基本代表在一定设防烈度下该类结构的地震易损曲线。

[ 1 ] 梁兴文, 叶艳霞. 混凝土结构非线性分析[M].北京: 中国建筑工业出版社, 2015.

[ 2 ] 于晓辉. 钢筋混凝土框架结构的概率地震易损性与风险分析[D]. 哈尔滨: 哈尔滨工业大学, 2012.

[ 3 ] 何益斌, 李艳, 沈蒲生. 基于性能的高层混合结构地震易损性分析[J]. 工程力学, 2013 (8):142-147. HE Yibin, LI Yan, SHEN Pusheng. Performance-based seismic fragility analysis of tall hybrid structures[J]. Journal of Engineering Mechanics, 2013 (8):142-147.

[ 4 ] 刘阳冰. 钢-混凝土组合结构体系抗震性能研究与地震易损性分析[D]. 北京：清华大学, 2009.

[ 5 ] YANG T P. MOEHLE J, BOZORGNIA Y, et al. Performance assessment of tall concrete core-wall building designed using two alternative approaches [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(11):1515-1531.

[ 6 ] KWON O, ELNASHAI A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure [J]. Engineering Structures, 2006, 28(2): 289-303.

[ 7 ] PORTER K A, BECK J L, SHAIKHUTDINOV R V. Sensitivity of building loss Estimates to major uncertain variables[J]. Earthquake Spectra, 2002, 18(4):719-743.

[ 8 ] 高层建筑混凝土结构技术规程:JGJ3—2010 [S]. 北京: 中国建筑工业出版社, 2011.

[ 9 ] 傅学怡. 实用高层建筑结构设计[M]. 北京: 中国建筑工业出版社, 2010.

[10] Quantification of building seismic performance factors，ATC-63 Project Report (90% Draft) [R]．FEMA P695/April 2008．

[11] 陆新征, 叶列平, 繆志伟.建筑抗震弹塑性分析[M]. 北京: 中国建筑工业出版社, 2009.

[12] PORTER K. Analytical derivation of seismic vulnerability functions for highrise buildings[R]. Global Vulnerability Consortium, 2013.

[13] CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4):526-533.

[14] FEMA. Multi-hazard loss estimation methodology earthquake model, HAZUS-MH MR3 Technical Manual[M]. Washington. D.C, 2003.

[15] 建筑抗震设计规范: GB 50011—2010[S]. 北京:中国建筑工业出版社, 2010.

Seismic fragility of RC frame-core wall structures

ZHENG Shansuo, ZHANG Yixin, QIN Qing, YANG Wei, GAN Chuanlei, ZUO Ying

(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

In order to establish fragility curves of high-rise RC frame-core wall structures, nine typical RC frame-core wall structures with uniform story height, different spans and earthquake fortification intensity were designed and numerically modeled. Considering the randomness of earthquake ground motions input, their seismic responses were obtained through nonlinear dynamic time history analysis adopting the finite element software Perform-3D. Ultimate damage states of all structures were defined on the basis of current seismic design code to build the corresponding seismic fragility curves. The influences of structural span and seismic fortification intensity on structures’ seismic fragility were analyzed. The results showed that low seismic fortification intensity makes no obviuos differences among structure vulnerability curves, while with increase in the intensity, the differences become obvious; although spans are divers, the fragility curves are similar under the same seismic fortification intensity; so, the design uncertainties have smaller effects on structures’ seismis fragility. The results provided a reference for the seismic loss estimation of city high-rise buildings.

high-rise RC frame-core wall structures; vulnerability curve; input of earthquake ground motion; structural design

国家科技支撑计划(2013BAJ08B03)；教育部高等学校博士学科点专项科研基金(20136120110003)；陕西省科研项目(2013JC16;2014JQ7231)

2015-05-28 修改稿收到日期：2015-10-11

郑山锁 男，教授，博士生导师，1960年生

张艺欣 女，硕士生，1991年生

TU375