行走人群-结构相互作用模型研究

高延安, 杨庆山

(北京交通大学 土木建筑工程学院 结构风工程与城市风环境北京市重点实验室,北京 100044)

行走人群-结构相互作用模型研究

高延安, 杨庆山

(北京交通大学 土木建筑工程学院 结构风工程与城市风环境北京市重点实验室,北京 100044)

人群中每个行人简化为一个集中质量和两个弹簧阻尼器腿的模型，利用拉格拉日方程建立了多人行走状态下的人群-结构相互作用模型。首先利用该模型研究了人群引起结构的响应和人群-结构系统的模态特性改变，然后分析了结构响应和系统模态随着人群数量的变化而改变，最后比较了在队列和并排两种不同行走状态下人群结构系统的响应和模态特性的变化。数值分析表明结构的响应和模态特性随着人群数目增加而变化增大，然而行人在结构上分布较为均匀的纵向行走方式能够有效降低结构的响应，为减轻结构的剧烈波动，在人行桥设计时建议采用窄的截面宽度或者在桥面上设置纵向疏导设施以避免人流集中对结构的不利影响。

数值模拟；人群-结构相互作用；模态特征；结构响应；人群行走方式

随着材料科学的发展和人们生活质量的提高，在满足规范的条件下设计的结构质量越来越轻，跨度越来越大，其导致结构的频率和阻尼耗能能力降低[1]。BACHMANN等[2]研究表明随着结构跨度的增加，自身的阻尼和频率会急剧下降。承受人群活动的低阻尼和频率结构往往容易发生共振引起结构的剧烈波动。据不完全资料统计，20世纪由人类活动引起的桥梁垮塌事故达40多起。在2000-06-10，伦敦千禧桥[3]开放当天由于行人经过该桥梁时引起结构的剧烈侧向振动而被迫关闭，该起事故后来引起了全世界1 000多家的媒体广泛关注和报道。为理解人与结构的相互作用，许多学者做了大量的研究工作。HAUKSSON[4]分别使用多自由度和单自由度模型分析了伦敦千禧桥的动力性能。NIKKHOO等[5]研究了简支梁在承受移动质量块作用下的动力响应和结构振动控制的方法。ZHOU等[6]用分布的弹簧质量块模拟人群研究了人群与结构的相互作用。简方梁等[7]考虑有序排列人群荷载、BS5400荷载和随机人群荷载三种模式下的人致振动响应，研究表明步频对结构的加速度影响最大。陈建英等[8]用单质量-弹簧-阻尼器作为人的模型，研究了5个人分布于简支梁上的结构与人相互作用，其数值模拟表明人会显著降低结构的第1阶模态频率和增大对应阻尼比。王海等[9]用一个具有分布质量、阻尼和刚度的动力学模型模拟附着于梁上的人体，其研究表明人能够显著影响结构的频率和阻尼比，人位于梁中跨时对结构的阻尼比和频率影响最大，其也研究了人群数量的增长对梁的动力特性影响。QIN等[10]用质量-阻尼-弹簧双腿动力学模型模拟行人，研究了简支梁与行走行人的相互作用。宋志刚等[11]从社会力模型角度和人桥相互作用的机理出发探索了人桥相互作用的动力放大系数，该法考虑了负阻尼的影响且与时程分析结果基本一致。目前多数研究集中在不考虑人的移动下的人群-结构模型或者单人-结构模型，鲜有学者研究多人行走下的人群-结构相互作用。

采用一个集中质量和考虑两条无质量的弹簧-阻尼腿模拟行人，多个具有该模型组成的人群通过简支梁的行走人群-结构相互作用作为研究对象，考虑实际情况中行人的水平位移和速度不依赖于动力方程，利用拉格拉日方程建立行走人群-结构相互作用的动力方程，数值分析了行走人群下结构的动力响应以及对结构模态特性的影响。动力方程物理符号见表1。

表1 动力方程物理符号

1 行走人群结构相互作用模型

通过用一个质量和两个具有弹簧阻尼器组成的腿模型建立单人行走下的行人-结构模型，他们的数值研究表明该行人模型能够很好的模拟行人-结构相互作用。本文首先利用上述行人模型建立了多人行走下的人群-结构模型，根据实际行走中行人的行走速度不依赖于动力方程，故文中模型的行人水平自由度考虑为已知量，其不仅更加符合实际情况而且降低了方程的自由度。人群-结构模型如图1所示，假设有χ个人行走于一个简支的Euler-Bernoulli梁上，从中任意挑选出第(q)个人(如图1下部的局部放大图所示)，该行人简化为一个集中质量加两个弹簧-阻尼器模型。该行人的集中质量用m(q)表示，行人腿的模态特性用附着于腿上的弹簧和阻尼器模拟。设定梁左端为行人-结构系统的坐标原点，水平右方向为x轴向，向上竖直方向为y轴方向。假定行人在行走过程中两条中至少有一条腿始终与梁接触，每个行人行走的水平位移和水平速度时程是已知的，行人只与结构发生相互作用，行人之间相互独立互不影响。

图1 行走人群-结构运动模型

人行桥用一个等截面简支的Euler-Bernoulli梁模拟，根据Lagrange方程，可以获得如下行走人群-结构系统的动能和势能

(1a)

(1b)

(2)

式中:{φi(x),i=1,2,…}为满足结构边界条件的梁振型函数;{Yi(t),i=1,2,…}为满足初始条件的结构广义位移;行人的前腿和后腿长度分别可以表达为

(3a)

(3b)

(4)

(5a)

(5b)

前后腿的轴向虚位移可以表示为：

(6a)

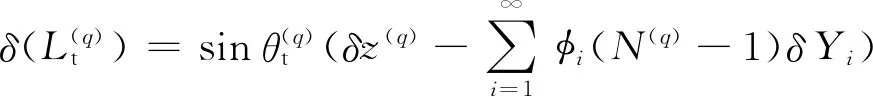
将式(5)带代入式(4), 系统虚功可以表达为

(7)

利用Lagrange方程，可得到系统能量与系统广义力之间的关系式如下

(8)

将式(1)代入式(8)后利用式(4)以及式(8)的变量对应关系，最终可以获得行走人群-结构系统的动力方程如下：

(9)

(10a)

(10b)

(10c)

(10d)

(10-e)

式中的系数如下所示：

Φi,j(N(q))=φi(N(q))φj(N(q))(i,j=1,2,…,n)

(i=1,2,…,n;q=1,2,…,χ)(q=1,2,…,χ)

2 人群-结构系统的模态分析

由于所建立的人群-结构动力方程中的阻尼和刚度矩阵是随时间变化的，行人腿的阻尼比结构本身阻尼要高很多，系统方程中行人和结构形成的新阻尼为非比例阻尼，系统的模态特性不能再采用RAYLEIGH阻尼，采用状态空间法[14]进行瞬时模态分析。定义状态空间矩阵和向量如下

(11a)

状态空间中，系统动力方程(9)可以变为

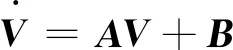
(11b)

利用对矩阵A的特征值求解，可以获得系统的模态特性如下所示

A{φ}i=λi{φ}i

(11c)

式中:λi和 {φ}i分别为矩阵A第i阶的特征值和特征向量，系统的第i阶频率fi和阻尼比ξi可以获得如下式所示

(11d)

显然，根据式(10b)和式(10c)可知，系统的阻尼和刚度矩阵是时变的，故可以求得系统的阻尼和频率时程曲线。

3 数值模拟

3.1 人群-结构相互作用分析

表2 空梁结构的模态频率和阻尼比

(a) 人群-结构系统的频率变化曲线

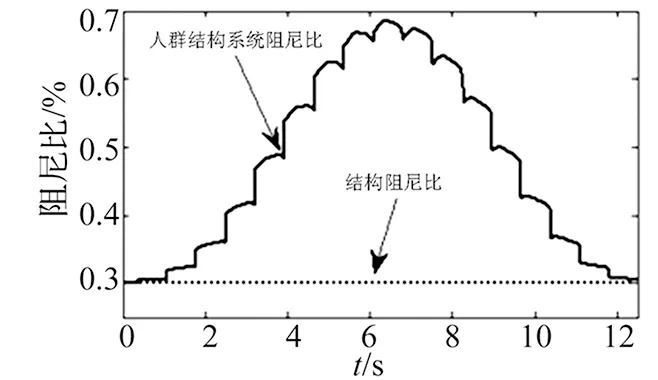
(b) 人群-结构系统阻尼比变化曲线

从图2可知，随着人群从梁端向一端行走时，系统的频率先减小后增大，而系统的阻尼比却呈现出相反的趋势，当人群走到梁中跨位置时，系统的频率达到最小，而阻尼比达到最大。而在人群全部进入结构前后离开结构后，梁的频率恢复到结构自然频率，阻尼比同样恢复到结构的自然阻尼比。可见人群作用于结构上时整个系统的频率和阻尼会随着行人的位置不同而有所改变。整个系统柔性变大，而阻尼耗能能力有所增加，数值分析表明人群位于结构中跨时能够显著提高系统的阻尼耗能能力，然后带来不利的影响是使系统变得柔性增大，易于引起共振。该结论与文献[9-10]的研究一致，受人群作用下结构在中跨的挠度、速度和加速度时程曲线分别见图3、图4和图5。从上述三幅的结构响应图可以看出，人群位于跨中时结构的位移、速度和加速度响应都达到最大。图6中结构的加速度反应谱显示前两个峰值的频率分别为2.734 Hz和4.297 Hz，其低于结构的第一阶自振频率4.50 Hz。

图3 结构中跨的位移-时程曲线

图4 结构中跨的速度-时程曲线

图5 结构中跨的加速度-时程曲线

图6 加速度的功率谱密度

3.2 考虑不同行走状态下的数值模拟

为了进一步研究人群数量和人群行走状态对系统的模态特性的影响，选择了5～21个人之间人群数量为研究对象，分别以5人增幅为一组和2人增幅为一组进行了人群组合，行人参数与结构参数与上述算例相同；然后分别按照队列行走(行人位于梁的纵向轴线上)和并排行走(行人位于梁的横向轴线上)的两种方式对人群-结构的模态特性和跨中加速度响应进行比较研究。为了突出研究整个人群-结构之间的相互作用，队列行走时初始时刻的行人从梁的左端向右以0.5 m的间隔站立，整体人群在开始时都位于梁外。并排行走时，整个人群“一”字形站立于梁左端开始向右行走(见图7～图8)。

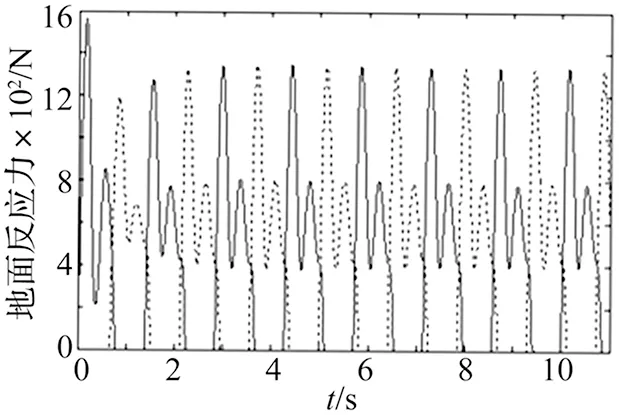
图7 行人的地面反应力

图8 行人质心竖向反应

3.2.1 队列行走

以5人增幅为一组的系统模态随时间变化如图9所示。人群在队列行走状态下，系统的频率随着人群数量的增长而减小，阻尼随着人群数量的增大而增大，但是随着人群以相等数目增加时，系统的频率和阻尼的变化幅值却逐渐出现平缓的趋势。系统的频率和阻尼的改变都表现出在人群大概位于梁的中跨时，二者的变化都最大。人群引起结构的加速度响应的均方根值随时间的变化如图10所示，图10中以每2 s为时长计算。由图10可知，随着人群数目的改变，加速度响应与结构模态特性表现出较一致的规律，行人大概位于跨中位置时结构的响应最大。

(a) 队列行走状态下系统的频率变化

(b) 队列行走状态下系统的阻尼比变化

图10 加速度响应的均方根值

3.2.2 并排行走

由数值模拟结果的图11可知，人群在并排行走状态下，系统的频率随着人群数量的增长而减小，阻尼随着人群数量的增大而增大，随着人群以相等数目的增加，系统的频率和阻尼的变化幅值并没有表现出平缓的趋势，而是呈现出等比例趋势的变化，系统的频率和阻尼的改变都表现出在人群大概位于梁的跨中位置时，二者的变化都最大。从图12给出结构加速度响应的均方根值可知，人群接近跨中位置时，结构的响应最大，同样随着人群相等数量的增加，加速度峰值呈现出近似于等幅值的增加。

3.2.3 两种行走方式比较

为进一步研究行人的不同行走分布方式引起人群-结构系统模态和加速度响应的变化，将行人以5个人为起始组，以每2个人增量为一组共9组人群的不同行走方式研究了结构行为的变化。然后以系统的模态频率和阻尼比峰值以及加速度最大值为对象进行了比较分析。从图13可以看出随着人群数量的增加，并排分布的行走方式引起系统的频率下降幅值比队列分布方式更大。相应对于图14中不同行走方式引起人群-结构系统的阻尼比的变化可以看出等人数条件下并排行走方式引起系统的阻尼比增加幅值更大。图15结构跨中的加速度峰值显示随着人群数量的增加，队列行走方式能有效减轻结构的振动。

(a) 并排行走状态下系统的频率变化

(b) 并排行走状态下系统的阻尼变化

图12 加速度响应的均方根值

图13 不同行走方式下系统的最小频率值

由此可以见，人行桥的宽度变窄时，人群趋于列队的方式行走能够减小人群对结构动力性能的影响和降低波动峰值；而当人行桥的宽度足足够大，多个人集中并排行走时能够增大人群对结构动力性能的影响同样也更易于增强结构的波动峰值，可见在人行桥设计时为避免过度振动，应考虑减小入口宽度或者减小桥板截面的宽度。

图14 不同行走方式下系统的最大阻尼比

图15 不同行走方式下结构跨中的加速度峰值

4 结 论

本文采用一个集中质量和具有刚度和阻尼器形成的两条腿模拟人体的动力模型施加于梁上，考虑行人的水平速度为已知条件下建立行走人群-结构相互作用的动力学模型，分析了行走人群-结构系统的动力特征，根据数值模拟可以得到以下结论：

(1) 研究人对结构的影响，将人作为具有质量、阻尼和弹簧的动力双腿模型作用于结构上是合理的。文中利用Lagrange方程建立了5个人从梁的左端行走到右端的相互作用动力学模型，通过数值模拟与已有文献的对比，模拟结果是合理的。

(2)数值分析表明行走人群下会对结构的动力特性有显著改变，主要表现在人群-结构系统的阻尼比增大，频率减小，相对而言阻尼比变化幅值更明显。

(3)通过不同人群数量在两种行走状态下对人群-结构模态特性的影响分析表明，相比而言人群按照纵向排开的行走方式比横向排开的行走方式能够有效降低对结构模态特性的影响和减小结构振动幅值，故在人行桥设计时建议在满足使用要求的条件下减小桥板的横向宽度或者在桥板上设置纵向疏导设施。

[ 1 ] HUANG Minghui. Dynamic characteristics of slender suspension footbridges[D]. The Ph. D thesis, Queensland University of Technology, May 2006.

[ 2 ] BACHMANN H, AMMAN W. Vibrations problems in structures: Practical guidelines[M]. 2nd ed., Birkhäuser, Basel, Switzerland, 1997.

[ 3 ] DALLARD P. The london millennium footbridge[J]. The Structural Engineer, 2001, 79 (22): 17-31.

[ 4 ] HAUKSSON F, Dynamic behavior of footbridges subjected to pedestrian-induced vibrations[D]. Master’s Dissertation of Lund University of Sweden, 2005.

[ 5 ] NIKKHOO A, ROFOOEI F R,SHADNAM M R. Dynamic behavior and modal control of beams under moving mass[J]. Journal of Sound and Vibration,2007(306):712-724.

[ 6 ] ZHOU Ding, JI Tianjian. Dynamic characteristics of a beam and distributed spring-mass system[J]. International Journal of Solids and Structures,2006(43):5555-5569.

[ 7 ] 简方梁，吴定俊，李奇. 上海虹桥车站人行走廊人致振动分析[J]. 振动与冲击, 2010, 29(8): 136-140. JIAN Fangliang, WU Dingjun, LI Qi, The vibrational analysis of pedestrian corridor about Shanghai Hongqiao station[J].Journal of Vibration and Shock, 2010, 29(8): 136-140.

[ 8 ] 陈建英，方之楚. 人-结构相互作用动力学建模研究[J]. 振动与冲击, 2007, 26(6):10-15. CHEN Jianying, FANG Zhichu. Study on modeling of human occupants-structure dynamic interaction[J]. Journal of Vibration and Shock, 2007, 26(6): 10-15.

[ 9 ] 王海，周叮，王曙光. 人-梁相互作用动力学模型研究[J].工程力学, 2010, 27(5): 14-20. WANG Hai, ZHOU Ding, WANG Shuguang, Modeling of the dynamic interaction of human occupants and beam[J]. Engineering Mechanics, 2010, 27(5): 14-20.

[10] QIN J W, LAW S S, YANG Q S,et al. Pedestrian-bridge dynamic interaction, including human participation[J]. Journal of Sound and Vibration,2013(332):1107-1124.

[11] 宋志刚，张尧. 人-桥侧向动力相互作用下的动力放大系数分析[J].振动与冲击, 2015, 34(1):19-23. SONG Zhigang, ZHANG Yao, Analysis of the dynamic amplification factor of lateral structural vibration induced by crowd-bridge interaction[J]. Journal of Vibration and Shock, 2015, 34(1): 19-23.

[12] 克拉夫，J·彭津.结构动力学[M]. 王光远等译. 2版.北京:高等教育出版社，2006.

[13] Juang J N, Applied system identification[M]. Englewood Cliffs, NJ, USA: Prentice Hall, 1994.

[14] 聂建国，陈宇，樊健生. 步行荷载作用下单跨人行桥振动的均方根 加速度反应谱法 [J]. 土木工程学报, 2010，43(9): 109-117. NIE Jianguo, CHEN Yu, FAN Jiansheng, RMS acceleration response spectrum method for single span footbridges under pedestrian load[J].China Civil Engineering Journal, 2010, 43 (9): 109-117.

A walking crowd-structure interaction model

GAO Yanan, YANG Qingshan

(Beijing Municipal Key Laboratory of Structural Wind Engineering and Urban Wind Environment, School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)

Each pedestrian was simplified as a lump mass and two spring-damper legs and a walking crowd-structure interaction (CSI) model was established using Lagrange’s equations. First of all, the structural responses and dynamic characteristics of the crowd-structure system were studied. Secondly, the structural responses and the modal changes versus the number of people were analyzed. Finally, under two different walking styles including queue and side by side, different structural responses were compared. The simulation analysis showed that the changes of the structural response and modal features of the crow-structure system increase with increase in number of people; however, the walking style of queue with a more uniform crowd distribution can effectively reduce dynamic responses of the structure; in order to avoid resonance or excessive fluctuation, a narrow cross-section and longitudinal dredging facilities on a bridge deck are recommended for footbridge designs.

numerical simulation; crowd-structure interaction; modal characteristics; structural response; walking styles of crowd

国家自然科学基金重大研究计划重点支持项目(51338001)

2015-04-23 修改稿收到日期：2015-11-30

高延安 男，博士生，1986年生

杨庆山 男，博士,教授，1968年生

TU311.3; O 313