多孔铝板高速撞击声发射定位方法

李凌江，刘武刚，王建民，孔凡金，刘振皓

（北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076）

多孔铝板高速撞击声发射定位方法

李凌江，刘武刚，王建民，孔凡金，刘振皓

（北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076）

目前，声发射定位技术在空间碎片撞击航天器事件中的撞击源定位问题中得到了广泛研究。在定位算法上，声发射信号传播机理的复杂性表现为输入量的随机性；多次撞击的复杂性则表现为声发射信号传播的弯曲路径。文章针对多孔铝板声发射定位问题进行研究，采用伽马分布对声发射信号传播的弯曲效应进行建模，采用相对时间差方法对声源进行定位，最后通过仿真分析对所提供的模型与算法性能进行了数值演示。该方法可应用于空间碎片撞击航天器的撞击源定位与损伤评估。

高速撞击；声发射技术；多点定位；带孔板；弯曲路径

0 引言

随着航天器发射数量的增多，空间碎片对在轨航天器造成的威胁已成为世界航天大国所关注的问题。在轨撞击感知系统能够为受撞击的航天器结构提供损伤状态评估，其中声发射技术能够实现撞击源定位、损伤特征提取及损伤模式识别等功能，成为具有应用潜力的一种监测手段[1-3]。由于被撞击结构自身的复杂特性，以及多次撞击对结构的损伤影响，声发射信号在结构中的传播机理与规律十分复杂。

针对典型航天器结构的撞击源定位技术在近年来得到了深入的研究，解决了不同结构的撞击定位问题，使不同工况下的定位精度有了提高。刘武刚等[4-5]利用二级轻气炮发射球弹丸模拟空间碎片对航天器的撞击，采集铝合金板的高速撞击声发射信号，根据高速撞击信号的特征，分别采用门槛时差及基于小波分析的定位方法进行了高速撞击的定位研究。刘治东等[6]利用虚拟波阵面的概念提出了一种应用于层合板的多传感器声发射源定位方法，在玻璃/环氧单向铺设层合板与正交铺设层合板上对铅芯折断波源进行了定位试验。庞宝君等[7]还利用希尔伯特-黄变换技术分析声发射信号特征，改进了A0模态到达时刻的确定算法，改进后的线定位方法和双时标法可有效应用于各向同性板的定位。王晓宇等[8]对航天器密封舱加筋壁板碎片撞击监测技术进行了研究，提出一种基于损伤概率成像的冲击定位方法，避免了求解双曲线方程的过程，并能提供更多冲击特征信息。上述工作主要集中于对单次撞击损伤定位的研究，源定位模型并没有考虑多次撞击对定位精度的影响。而实际工程中，航天器结构会遭受到多次撞击，声发射波的传播路径将发生改变，基于声发射波直接传播得到的源定位模型将不能保证定位精度的要求。如何建立多次撞击下的损伤源定位模型以提高定位精度，成为实际工程面临的关键技术问题。

空间碎片超高速撞击航天器结构会引起瞬态弹性应力波的释放，并以球面波的形式在结构中传播。这种应力波被安装于航天器结构的传感器采集并转换为声发射信号后，就可以利用声发射定位技术对这些信号进行分析并确定撞击位置。声发射定位技术主要包括2个方面的内容：一是确定声发射信号到达各个传感器的时刻，二是根据信号到达时间对信号源定位[9]。

到达时刻的确定方法主要有门槛值法、小波分析法、时延估计法等。门槛值法主要是一种时域波形分析方法，其思想是通过设定适当的阈值，将特定模态的幅值首次大于阈值时所对应的时刻作为该模态的到达时刻[4]。小波分析法是一种时频分析方法，即从小波谱中抽取指定频率的小波能量系数，并将该系数的首个峰值所对应的时刻作为该频率的到达时刻[5]。时延估计法是一种时域分析方法，其思路是提取因传输距离不同而引起不同传感器接收到目标声源信号之间的到达时间差[10-11]。

声源定位方法主要有基于最大输出功率的可控波束声源定位技术、基于高分辨率谱估计的声源定位技术、基于时延估计的声源定位技术等，其中基于时延估计的声源定位技术应用最为广泛[10-13]。

本文沿用时延估计法的思路，结合概率统计方法，针对带孔板的多次撞击声发射定位问题，建立多次撞击下损伤定位模型，并进行仿真分析。

1 带孔板定位问题概述

空间碎片高速撞击航天器后，会在航天器表面留下洞孔。这些洞孔的存在将影响下一次撞击应力波的传播路径与波形，尤其是多次撞击后，若使用无孔声源定位算法定位时，留下的孔洞将产生系统性定位偏差。单孔时，如图1所示，以圆圈代表孔洞，理想情况下，当孔洞不存在时，应力波沿虚直线从点A传播到点B；当孔洞存在时，应力波将沿实线箭头曲线从点A传播到点B。多孔时，应力波按照单孔时的原则传播。

图1 应力波传播路径沿孔洞弯曲示意图Fig.1 The curving effect of elastic wave propagating along an orifice

空间碎片撞击航天器时有如下特点：1）航天器表面的撞击损伤位置具有随机性；2）不同撞击之间相互独立；3）撞击速度很高，可以近似认为只在航天器表面留下平整的孔洞。

根据上述特点，将多次撞击下航天器表面上的定位问题简化为已经存在一定数量孔洞的板面上的声源定位问题。为简化分析，根据经验对带孔板与传感器布局作如下假设：

1）假设基板（无孔洞时的板）为各向同性，应力波在板上的传播速度恒定，设为v；

2）孔的个数为n，半径为R，孔位置在板上稀疏分布，每个孔的位置为随机产生；

3）传感器阵列采用矩阵布局，坐标为

在上述假设下，时延估计思路下的带孔板定位算法可分为2个步骤：1）确定声发射信号到达各个传感器的到达时刻；2）根据到达时刻的模型求解声源位置。

2 多点定位模型与定位方法

2.1 到达时刻确定算法

为克服人为设置信号到达时间阈值存在的主观性与任意性，提出一种基于 AIC-信息准则（Akaike Information Criterions）确定信号到达时间的方法。AIC-信息准则是一种建立在熵概念下的评估统计模型拟合优良性的标准。

对于信号序列x1:N={x1,x2, …,xN}，AIC-信息函数定义为

上述AICk的含义是2段信号x1:k与xk:N之间的相对熵，它描述2个序列之间的相似性。对于一个声发射信号，AICk在信号到达时刻取得极小值点。如图2中红色曲线所示。

图2 声发射信号的AIC准则函数Fig.2 The AIC criterion of acoustic emission signal

2.2 多点定位模型

对于带孔板上的声源定位问题作如下模型假设：

1）没有孔洞存在时，声源点X至传感器Pk的传播路径为直线，其路径长度为dk=‖X-Pk‖，其中‖·‖为欧氏距离。

2）孔洞的存在使得应力波从声源点X至传感器Pk的传播路径发生弯曲，其实际传播路径长度为Dk=v(tk-t*)，其中t*为声源产生时刻，tk为声信号到达第k个传感器的时刻。

3）空间碎片撞击航天器表面的位置是任意的，且每一个位置被撞击机会相同，因此可以认为孔在板面上的分布为均匀分布。在此假设下，任意两点之间的弯曲距离Dk-dk与此两点之间的直线距离成正比，且为一个正的随机变量，即Dk-dk=dk·ηk，ηk为弯曲效应，设其服从伽马分布ηk～Γ(N,λN)，λN为弯曲效应参数，与孔的直径、孔的个数、板的大小等有关，不同点上的弯曲效应相互独立。以图1为例进行说明，弯曲效应是APQB间的实线弯曲路径比AB间的虚直线多出的距离与线段AB长度的比值，路径上存在多孔时类似。

4）测量过程中存在加性随机误差ε，假设其服从正态分布N(0,)。

在上述假设下，孔洞的存在实际上是对声发射信号的传播路径附加了弯曲效应。采用到达时间差的思想建模，模型如式(2)所示，

2.3 带孔板多点定位算法

2.3.1 模型参数学习

式(2)中的待定参数(N,λN,σε)可通过边际极大似然法从训练数据ΔD={ΔDi,k: 1≤i≤n,i≠k}获得。

以第k个传感器为基准点的对数似然函数为

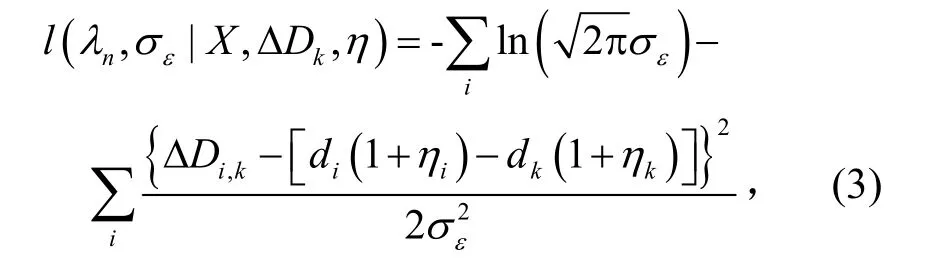
计算式(3)关于弯曲效应η期望，得到

轮换基准点k得到代价函数

在带孔板上多个位置分别采集声发射信号{Xt:1≤t≤m}，通过到达时间确定方法得到每个声发射信号位置的到达时间阵列，计算到达距离差序列{ΔDt}。

m个位置的总代价函数为

极大化上述代价函数得到

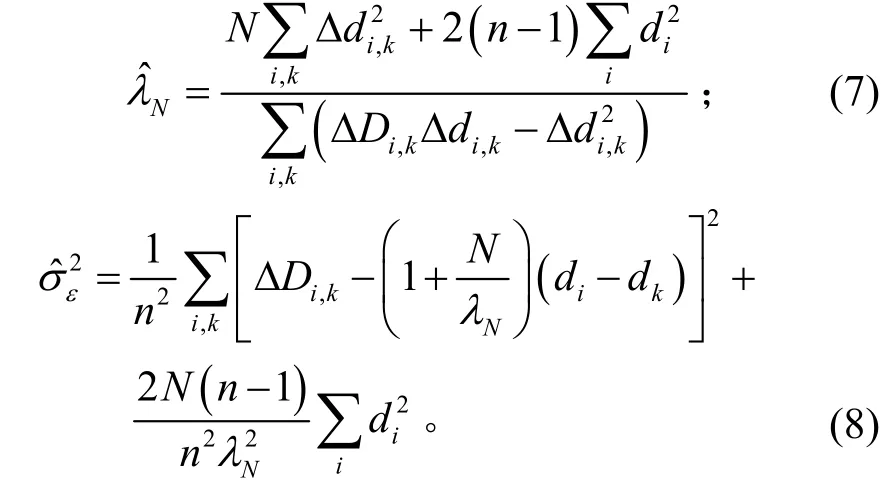
参数N没有解析表达式，需要用数值方法计算，即：将式(7)、式(8)代入式(6)，然后计算式(6)的极大值得到参数N的估计。

2.3.2 声发射源定位

在获得模型参数后，根据采集到的声发射信号对声发射源进行定位。定位方法为极小化过程，可表示为

一般情况下，式(9)没有解析形式，需要通过优化方法得到数值解。极小化过程中一般会出现局部极值问题，但对于实际应用问题，声源点可以通过矩形法等方法确定大概位置，并且局部极值个数往往只有几个，因此可以通过尝试多次初值的方法得到全局极值。

3 算法性能仿真分析

在式(3)假设下，多个孔洞对声发射定位精度的影响问题可转换为弯曲效应对定位精度的影响问题。

3.1 算法性能度量准则

对于带孔铝合金板，由于孔洞的存在以及传感器的位置设计，使传感器网络对不同位置的定位精度存在差别。故将所有位置的平均定位精度作为衡量算法整体性能的指标：平均定位精度越高，表明算法的定位性能越好。

3.2 仿真分析

铝合金板尺寸为250 cm×200 cm，传感器布局采用5×5等间距阵列方案。弯曲效应参数满足条件99%分位点为10.66%，即：对于给定的任意孔洞分布，板面上任意两点之间附加的弯曲效应，平均而言有99%的弯曲效应小于10.66%。例如，对于距离为1 m的两点，由弯曲效应附加的距离长度以0.99的概率覆盖10.66 cm。

在上述参数条件假定下，考虑本文提出的定位算法在板面上不同位置的定位表现。随机在板面上指定100个位置，如图3中的蓝色“*”所示。采用本文提出的定位算法对每一个位置进行定位，其定位结果如图3中的红色“·”所示。可以看出，板面上任意位置的定位误差都很小，算法具有较高的精度与稳定性。使用蒙特卡罗方法计算得到板上的平均定位精度为1.3 cm。

图3 带孔板面上不同位置的定位精度Fig.3 The location accuracy of some random positions on a poriferous plane

4 结束语

针对铝合金板上有多个洞孔存在时的声源定位以及定位算法的性能评估问题，从概率统计的角度建立了定位模型与定位算法。主要思想为整体考虑铝合金板上的多个孔洞产生的弯曲效应，认为其服从伽马分布。在此假设下，带孔板上声源的定位算法被分解为2个步骤：1）孔洞弯曲效应分布参数学习；2）求解模型对声源进行定位。仿真结果表明，本文提出的定位算法在整体性能上表现出相对较高的精度和较好的稳健性；提出的模型与方法可应用于空间碎片撞击航天器的撞击源定位与损伤评估。

（

）

[1]李怡勇, 沈怀荣, 李智.空间碎片环境危害及其对策[J].导弹与航天运载技术, 2009(6): 31-35 LI Y Y, SHEN H Y, LI Z.Space debris’s hazard andcountermeasures[J].Missiles and Space Vehicles, 2009(6): 31-35

[2]刘武刚, 庞宝君, 王志成, 等.天基在轨空间碎片撞击监测技术的进展[J].强度与环境, 2008, 35(1): 57-64 LIU W G, PANG B J, WANG Z C, et al.Technique advances about space debris in-situ impact-sensingsystem[J].Structure & Environment Engineering, 2008, 35(1): 57-64

[3]庞宝君, 刘治东, 张凯, 等.空间碎片撞击在轨感知技术研究综述[J].航天器环境工程, 2010, 27(4): 412-419 PANG B J, LIU Z D, ZHANG K, et al.A review of studies of onboard sensor systems for space debris impact on spacecrafts[J].Spacecraft Environment Engineering, 2010, 27(4): 412-419

[4]刘武刚, 庞宝君, 孙飞, 等.高速撞击的声发射源定位[J].无损检测, 2008, 30(3): 168-170 LIU W G, PANG B J, SUN F, et al.Acoustic emission detection and location for hypervelocity impacts[J].Nondestructive Testing, 2008, 30(3): 168-170

[5]刘武刚, 庞宝君, 韩增尧, 等.基于小波技术的高速撞击声发射源定位[J].高技术通讯, 2009, 19(2): 181-187 LIU W G, PANG B J, HAN Z Y, et al.Acoustic emission detection and location for hypervelocity impacts based on wavelet transform[J].Chinese High Technology Letters, 2009, 19(2): 181-187

[6]刘治东, 庞宝君, 唐颀.基于虚拟波阵面的层合板声发射源定位[J].压电与声光, 2010, 32(3): 493-497 LIU Z D, PANG B J, TANG Q.Acoustic emission source location in laminated plates based on virtual wave front[J].Piezoelectrics & Acoustooptics, 2010, 32(3): 493-497

[7]庞宝君, 刘治东, 唐颀.基于HHT变换的声发射源球面定位方法[J].无损检测, 2010, 32(1): 1-5 PANG B J, LIU Z D, TANG Q.Acoustic emission source sphere location method based on HHT[J].Nondestructive Testing, 2010, 32(1): 1-5

[8]王晓宇, 张超, 孙维, 等.航天器密封舱加筋壁板碎片撞击监测技术研究[J].实验流体力学, 2014, 28(4): 70-77 WANG X Y, ZHANG C, SUN W, et al.Research on structural health monitoring method for locating space debris impact on spacecraft seal structures[J].Journal of Experiments in Fluid Mechanics, 2014, 28(4): 70-77

[9]沈功田, 耿荣生, 刘时风.声发射源定位技术[J].无损检测, 2002, 24(3): 114-117 SHEN G T, GENG R S, LIU S F.Acoustic emission source location[J].Nondestructive Testing, 2002, 24(3): 114-117

[10]刘武刚.基于声发射的空间碎片撞击在轨感知技术研究[D].哈尔滨: 哈尔滨工业大学, 2008

[11]刘治东.空间碎片在轨感知系统中FRP层合板声发射定位技术研究[D].哈尔滨: 哈尔滨工业大学, 2008

[12]HENSMAN J, MILLS R, PIERCE S G, et al.Locating acoustic emission sources in complex structures using Gaussian processes[J].Mechanical Systems and Signal Processing, 2010, 24: 211-223

[13]KIM D H, PARK Y.Development of moving sound source localization system[J].Electronic Journal Technical Acoustics, 2006,11: 11-18

（编辑：闫德葵）

Acoustic emission localization of hypervelocity impact in perforated plate

LI Lingjiang, LIU Wugang, WANG Jianmin, KONG Fanjin, LIU Zhenhao
(Science & Technology on Reliability & Environmental Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)

Acoustic emission localization technology is widely used to locate the impact source in the space debris impact.The propagation mechanism of acoustic signals in structures is very complex because of the complex characteristics of the structure itself and multiple impacts involved.The complexity of the propagation mechanism leads to the input randomness in the algorithm, while the complexity of multiple impacts leads to the curved path of the acoustic emission signal propagation.The acoustic emission localization of the space debris impacting on an aluminum alloy plate is discussed in this paper, and a bending effect model is established as Gamma distribution, which considered the randomness of the propagation path, and Delta-T method is employed to locate the acoustic source.A simulation is presented to demonstrate the capability of the model and the algorithm at last.The method proposed can be used for impact source location and damage assessment of space debris impacting.

hypervelocity impact; acoustic emission; multi-point location; perforated plate; curved path

O384; TB115

：A

：1673-1379(2016)06-0589-05

10.3969/j.issn.1673-1379.2016.06.003

李凌江（1985—），男，博士学位，主要从事统计学习&机器学习、试验设计、工业可靠性等研究。E-mail: zlingxier@163.com。

2016-10-28；

：2016-12-20