基于鲁棒H∞控制策略的Hexapod平台低频微振动隔离设计

徐舒寒，孔永芳，黄 海

（北京航空航天大学 宇航学院，北京 100191）

基于鲁棒H∞控制策略的Hexapod平台低频微振动隔离设计

徐舒寒，孔永芳，黄 海

（北京航空航天大学 宇航学院，北京 100191）

文章采用一种基于混合灵敏度的鲁棒H∞控制策略来提高音圈电机驱动的柔性Hexapod平台隔振系统的低频特性；并利用一种基于非光滑优化算法的定结构解算方法快速求解得到低阶稳定的控制器，以解决传统解算方法中高阶复杂控制器难以实现的问题。通过仿真与试验进行频域和时域的验证分析，结果表明：所提出的振动隔离控制策略有效地降低了系统频响曲线的转折频率，提高了低频段的振动衰减率，使柔性Hexapod平台隔振系统的低频隔振效果显著提高。

振动隔离；低频；Hexapod平台；鲁棒H∞控制；定结构解算方法

0 引言

航天任务对有效载荷的精度要求越来越高，使得载荷对微振动十分敏感。航天器上有许多扰动源，如制冷机、反作用飞轮、太阳能电池阵驱动器、射频天线万向架、波导开关和姿轨控发动机等[1-3]，工作时都会产生随机振动和谐波振动[4]，对有效载荷的工作精度和稳定度造成影响。在轨卫星的微振动频率集中在 0.1～300 Hz，而姿态控制环路的带宽为0.05 Hz[5-6]。这意味着有效载荷支撑的振动隔离装置需要满足0.1 Hz以下位姿跟随、0.1 Hz以上振动隔离的要求，同时提高低频段的振动衰减率，即在更低的频段达到-20 dB的衰减效果。因此，航天任务对有效载荷支撑结构的振动传递特性提出了较高的要求。

一种基于Hexapod构型的六自由度并联机构[7]因其良好的结构稳定性和动力学特性而得到广泛应用，尤其是音圈电机驱动的Hexapod主被动一体化隔振装置[8]隔振效果显著。应用于Hexapod平台隔振控制的传统算法为Skyhook法[5]，通过积分力反馈方法改变结构阻尼，可以有效地消除系统中因被隔振设备质量和隔振基座刚度而引起的共振峰，达到低频跟随、高频隔振的目的。这类主动阻尼的隔振方法主要起到增加阻尼、拉平共振峰的效果。

当前的航天任务对隔振装置要求有更宽的隔离频带选择和更高的振动衰减率，这可以通过系统机械结构和隔振控制策略的改变来实现。对于系统机械结构改变的方法，可在作动杆中采用柔性更高的部件[9]，以降低与音圈电机并联弹簧的刚度。然而，刚度过低又会降低系统的高阶局部模态，影响隔振系统的高频特性[8]。因此，当机械结构已经达到设计极限值时，就需要采用改变隔振控制策略的方法来实现更低的转折频率。传统的PID方法可适量地降低系统的转折频率，但低频段振动衰减的效果不明显，只对高频段的衰减率产生影响；应用于HT/UW 平台[10]的线性二次高斯控制（linearquadratic- Gaussian control, LQG）可实现1.5 Hz的转折频率，并在5～20 Hz频率区间达到-20 dB的衰减率，但是在控制策略中需要采用2级传感器，且存在平台耦合问题。Honeywell公司的VISS平台[11]应用负载质量惯量反馈的方法实现了超低频的隔振控制，然而中高频段的隔振效果略有不足。

本文针对音圈电机驱动的柔性Hexapod隔振平台，提出了一种基于混合灵敏度的鲁棒H∞控制策略，以提高隔振系统的低频特性。通过配置算法中的权值函数，可以满足任意期望的截止频率和低频衰减率的需求，而无须对控制对象的结构做改变，使得一套隔振装置可以满足不同的指标需求，有效降低成本。不同于以往的H∞控制策略[12-13]所采用的DGKF[14]或LMI的控制器解算方法[15]，本文采用了一种基于非光滑优化算法的定结构解算方法[16]进行求解，得到了低阶稳定控制器。仿真和试验结果表明，所提出的控制策略能够有效地提高低频范围内的振动隔离效果。

1 Hexapod平台微振动隔离控制方法

1.1 控制系统建模

基于Cubic构型（见图1）的Hexapod平台是以立方体的2个斜侧面ABC和DEF作为平台的上、下平面，以立方体的6条棱边L1～L6作为作动杆。Hexapod平台中相邻两杆相互正交，使得各杆间的耦合作用可以忽略不计。同时，因为是微振动，上平面3个方向（x、y、z向）的运动可以由同向的1对作动杆控制，不受其他4个作动杆的干涉。因此，针对Cubic构型的Hexapod平台，采用分散控制策略，即采用 6个互相独立的单输入单输出（single input single output, SISO）控制方法，对控制对象的建模也简化为对单个作动杆的建模问题。

图1 Cubic构型Fig.1 Configuration of cubic model

单个作动杆的理论模型可以简化为一个弹簧阻尼系统，其动力学方程为

其中：杆端负载质量M=5 kg；xp为作动杆顶端位移量；阻尼系数C=14 N·s/m；音圈电机中膜簧的刚度K=12 407 N/m；F为音圈电机的输出力。以音圈电机输出力F作为模型输入量，以作动杆顶端加速度作为模型输出量，建立单个作动杆的动力学模型，模型的状态空间方程为

在单杆模型的基础上，结合鲁棒H∞控制策略中的混合灵敏度问题[17]，建立系统的控制模型，即广义系统的建模。广义系统为基于混合灵敏度的鲁棒H∞控制策略的控制对象，包括原控制对象模型、权值函数、广义输入和广义输出。如图2所示，其中，原控制对象模型为Hexapod平台单个作动杆模型，权值函数为Wn、Wb、W1和W2，广义输入为负载响应受到的环境噪声干扰ωn和底部振动扰动ωb。由于本文的隔振问题所关注的是负载加速度响应和主动控制力的大小，所以选取这2项分别连接各自的权值函数之后作为广义输出，即z1和z2。此外，u为控制系统的输入信号，即音圈电机的输出力F；y为控制系统的输出信号，即作动杆顶端的加速度与测量噪声之和。

图2 控制系统模型Fig.2 Model of the control system

在公式(2)的基础上可以得到广义系统的状态空间方程为

1.2 权值函数的选取

权值函数是系统性能需求的一种体现，例如系统的鲁棒性、抗干扰性、控制关注点等方面信息，也是对实际问题的一种考虑，例如驱动电机的输出极限、环境噪声等问题，因而权值函数的选取决定了控制器的设计效果。本文建立的广义系统应用了W1、W2、Wn和Wb等4个权值函数，分别连接在广义输入之后和广义输出之前，包含了对期望特性的考虑和对实际问题的参考。

如图3所示，权值函数W1体现了控制重心，针对重点关注的频段增大广义输出z1的相对权重，以保证控制效果；在此频段外减小权重，旨在降低不必要的控制输出。因而权值函数W1选择带通滤波器，通频带设置在重点控制的频率区间，通过修改通频带的频率区间和幅值即可以调整系统频响曲线的转折频率和衰减效果，本文设置的主控制带宽为1～100 Hz。权值函数W2体现了对驱动力饱和以及电机输出极限的考虑，本文中音圈电机的最大持续输出力为 30 N，因此权值函数W2选择20lg(1/30)=-29.54 dB的常值。Wn是噪声扰动的权值函数，考虑环境中的高频噪声，因而选取高通滤波器。底部扰动的权值函数Wb选择等值输出即可。

图3 权值函数的选取Fig.3 Selection of weight function

1.3 控制器的解算

一个标准化的H∞控制问题可以定义为从广义输入到广义输出的闭环传递函数的H∞范数的最小化问题，即对于给定的广义系统Gaug，寻找一个稳定控制器(s)，使其能够满足[18]

用于解算上述问题的方法主要有全阶控制器设计方法和定结构控制器设计方法2类。全阶控制器设计方法可以参数化被寻优的控制器，得到全局最优解，例如基于Riccati不等式的DGKF算法[14]和基于线性矩阵不等式的 LMI方法[15]。目前，DGKF算法被认为是求解H∞控制问题的非常有效而稳定的方法，但该方法要求系统满足5项严格的假设。LMI方法具有约束条件较宽松的优势，仅需要系统满足2项假设，并且能够解决非奇值和奇值问题。然而，用全阶方法设计的控制器阶数与建立的控制系统阶数相同，这种高阶控制器的实现对软硬件的要求非常高，星载设备难以实现[19]。定结构控制器设计方法允许优先设定控制器的阶数，应用非光滑优化算法[16]进行快速寻优，得到局部最优解，相比于全阶控制器，既不需要严格的假设条件，又可以得到易实现的低阶稳定控制器，因而本文选用定结构控制器设计方法。

针对上述问题，分别应用3种解算方法进行控制器的求解，控制器特性如表1所示。

表1 控制器特性对比Table 1 Comparison of features of the controllers

由表1可见：定结构解算方法中，设置控制器阶数只有 3阶，而全阶方法求得的控制器分别为16阶和15阶。相比于略微牺牲最优解的γ值，用定结构方法得到的低阶稳定控制器更具有可实现性。图4为3种控制器的奇异值曲线对比，在中低频段，3种控制器的性能完全相同；在高频段，全阶控制器仍有控制作用，定结构控制器不再有控制作用，系统主要依靠柔性部件的被动隔振作用进行隔振，节约了能源。

图4 3种解算方法求得控制器的对比Fig.4 Comparison of controllers obtained by three solvers

通过以上建模与解算求得连续系统控制器，选取采样频率1000 Hz进行离散化，得到离散系统控制器，即为

对比本文提出的鲁棒H∞控制方法与传统的积分力反馈控制方法，它们的计算结果如图5所示。

图5 H∞控制方法与积分力反馈方法的对比Fig.5 Comparison betweenH∞controller and integral force feedback controller

结果表明，基于混合灵敏度的鲁棒H∞控制方法能够有效降低系统的转折频率，实现更低频的振动衰减，同时低频段的振动衰减率提高显著。

2 Adams/MatLab联合仿真

在Adams中建立Hexapod平台模型，如图6所示，主要包括柔性上平台、下平台和6个作动杆，每个作动杆主要包括柔性连接铰、刚性杆体、膜簧、电机动子、电机定子和电机外壳等。建立 Adams/ MatLab联合仿真模型，以作动杆输出力为控制量，6个作动杆的顶端加速度作为控制反馈量，下平台六自由度的加速度作为底部扰动，上平台六自由度的加速度作为观测值，分别针对开环系统、传统积分力反馈方法闭环系统和鲁棒H∞方法闭环系统的下平台施加6个自由度的白噪声激励，得到整台在0.1～60 Hz频段的频域特性，如图7所示。鲁棒H∞方法闭环系统的转折频率可以控制在0.2 Hz以下，相比于传统的积分力反馈方法，6个自由度在低频段的振动衰减率都有明显提高。

图6 Hexapod平台的Adams模型Fig.6 Adams model of Hexapod platform

图7 开环/闭环系统频域特性仿真对比分析Fig.7 Comparison and analysis of open-loop / closed-loop simulation system in frequency domain

其中以z方向为例，进行控制器输出力的代价分析。图8为传统积分力反馈方法和鲁棒H∞方法在同种工况（下平台扰动为0.1～60 Hz正弦对数扫频）下的1号控制器输出力对比图。从图中可以看出，在中低频段，鲁棒H∞方法的输出力略大于积分力反馈方法，但没有付出过多的输出力代价，却得到了更低的转折频率和更高的振动衰减率，证明了鲁棒H∞方法的实际应用可行性。

图8 控制器输出力对比图Fig.8 Comparison of the controllers’ output forces

针对多自由度耦合的底部扰动工况也进行了一组仿真。例如，对下平台同时施加z向平动（幅值8 mg、频率1 Hz）、绕z向转动（幅值0.006 rad/s2、频率2 Hz）和绕x向转动（幅值0.003 rad/s2、频率3 Hz）的多自由度复合频率的振动扰动。图9所示为上平台6个自由度的加速度响应，第3 s加控制策略后，信号均衰减66%以上，控制效果显著，同时也验证了采用分散控制策略的可行性。

图9 上平台6自由度的加速度响应Fig.9 Acceleration responses of six DoFs of the upper platform

3 试验装置及试验验证

3.1 隔振控制试验装置

隔振控制试验装置原理如图10所示，主要包括隔振平台、隔振控制系统、悬吊系统、激励系统、数据采集系统等。其中，隔振控制系统主要由控制器、驱动器和配套的电源及连接线路等组成。悬吊系统主要包括支架和悬吊弹簧，用于抵消重力影响，以模拟微重力环境。激励系统采用本实验室自主研制的多自由度振动激励系统。数据采集系统主要由各传感器和信号处理器组成。试验装置如图11所示。

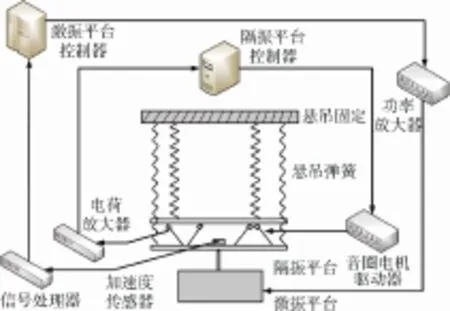
图10 隔振控制试验装置原理图Fig.10 Schematic diagram of the experimental system for vibration isolation control

图11 隔振控制试验装置Fig.11 The experimental system for vibration isolation control

3.2 试验结果与分析

由于试验条件限制，激振器的扫频范围选取2～12 Hz，进行z方向正弦扫频试验，如图12所示，其中，图12(a)为试验得到的开环不加控系统、积分力反馈方法和鲁棒H∞方法的系统频域特性对比图，图12(b)为从理论频响图（图5）中截取的对应频段的频响图。从频响图中可以看出，试验结果与理论解算结果相符，在低频段，鲁棒H∞方法的振动衰减效果与积分力反馈方法相比有明显的提高。

图12 开环/闭环系统频域特性试验对比分析Fig.12 Comparison and analysis of open-loop / closed-loop experimental system in frequency domain

针对多自由度耦合的底部扰动工况也进行了一组试验。下平台扰动选取低频1 Hz与共振峰5 Hz复合的z向正弦激励来进行隔振试验，图13为上平台的加速度时域响应。在第3 s开启H∞控制策略之后，最大振幅从18.75 mg降到8.54 mg，振动衰减了55%。可见，H∞控制策略实现了良好的控制效果。

图13 上平台加速度响应Fig.13 Acceleration response of the upper platform

4 结束语

为了降低柔性 Hexapod隔振平台的系统转折频率并提高低频段的振动衰减率，采用一种基于混合灵敏度的鲁棒H∞控制策略，通过基于非光滑优化算法的定结构解算方法进行快速求解，得到了低阶稳定的控制器。通过仿真与试验结果的频域和时域对比分析，证明了振动隔离的H∞控制策略能够有效地降低系统频响曲线的转折频率，验证了柔性Hexapod隔振系统具有显著的低频隔振效果。

（

）

[1]ULLIO R, MARTA F.SM98-109/433 Artemis micro-vibration environment prediction[C]//European Conference on Spacecraft Structures, Materials and Mechanical Testing.Braunschweig, Germany, 1999: 489-495

[2]BIALKE B.A compilation of reaction wheel induced spacecraft disturbances[C]//20thAnnual American Aeronautical Society Guidance and Control Conference.San Diego, AAS paper 1997-038

[3]JEDRICH N, ZIMBELMAN D, TURCZYN M, et al.Cryo cooler induced micro-vibration disturbances to the Hubble Space Telescope[C]//5thCranfield Space Dynamics Conference.Cambridge, UK, 2002-07

[4]BRONOWICKI A J.Vibration isolator for large space telescopes[J].Journal of Spacecraft & Rockets, 2006, 43(1): 45-53

[5]KAPLOW C E, VELMAN J R.Active local vibration isolation applied to a flexible space telescope[J].Journal of Guidance Control & Dynamics, 1980, 3(3): 227-233

[6]LIU C, JING X, DALEY S, et al.Recent advances in micro-vibration isolation[J].Mechanical Systems & Signal Processing, 2015, 56/57(1): 55-80

[7]STEWART D.A platform with six degrees of freedom[J].Proceedings of the Institution of Mechanical Engineers, 1965, 180(1): 371-386

[8]PREUMONT A, HORODINCA M, ROMANESCU I, et al.A six-axis single-stage active vibration isolator based on Stewart platform[J].Journal of Sound & Vibration, 2007, 300(3/4/5): 644-661

[9]THAYER D, CAMPBELL M, VAGNERS J, et al.Six-axis vibration isolation system using soft actuators and multiple sensors[J].Journal of Spacecraft & Rockets, 2002, 39(2): 206-212

[10]HAUGE G S, CAMPBELL M E.Sensors and control of a space-based six-axis vibration isolation system[J].Journal of Sound & Vibration, 2004, 269: 913-931

[11]HINDLE T, DAVIS T, FISCHER J.Isolation, pointing, and suppression (IPS) system for high-performance spacecraft[J].Proceedings of SPIE: The International Society for Optical Engineering, 2007, 6527: 5-12

[12]王东炜.Stewart平台隔振的主动控制研究[D].哈尔滨: 哈尔滨工业大学, 2014: 43-53

[13]吴迎.基于 Stewart平台的卫星微振动主动控制方法研究及装置优化设计[D].哈尔滨: 哈尔滨工业大学, 2014: 29-33

[14]DOYLE J C, GLOVER K, KHARGONEKAR P P, et al.State-space solutions to standardH2andH∞control problems[J].IEEE Transactions on Automatic Control, 1989, 34(8): 831-847

[15]GAHINET P, APKARIAN P.A linear matrix inequality approach toH∞control[J].International Journal of Robust & Nonlinear Control, 2010, 4(4): 421-448

[16]BRUINSMA N A, STEINBUCH M.A fast algorithm to compute theH∞-norm of a transfer function matrix[J].Systems & Control Letters, 1990, 14(4): 287-293

[17]POSTLETHWAITE I, TSAI M C, GU D W.Weighting function selection inH∞design[C]//Proceedings of the 11thIFAC World Congress.Tallin, Estonia, 1990-05: 104-109

[18]黄曼磊.鲁棒控制理论及应用[M].哈尔滨: 哈尔滨工业大学出版社, 2007: 32-61

[19]JOSHI A, KIM W J.System identification and multivariable control design for a Satellite UltraQuiet Isolation Technology Experiment (SUITE)[J].European Journal of Control, 2004, 10(2): 174-186

（编辑：肖福根）

Low-frequency micro-vibration isolation on Hexapod platform based on robust H∞method

XU Shuhan, KONG Yongfang, HUANG Hai
(School of Astronautics, Beihang University, Beijing 100191, China)

A robustH∞control strategy based on mixed sensitivity is proposed to improve the low-frequency characteristics of the flexible Hexapod vibration isolation system driven by voice coil motors.A stable low-order controller is obtained by a fixed-structure fast solver based on a non-smooth optimization algorithm for solving the implementation problem of high-order complex controllers by conventional methods.Results of simulation and experiment in frequency and time domains show that the proposed control strategy can effectively reduce the system corner frequency and improve the vibration attenuation rate at low frequencies.The isolation effect of the flexible Hexapod vibration isolation system at low frequencies is significantly enhanced.

vibration isolation; low frequency; Hexapod platform;H∞robust control; fixed-structure solver

TB535

：A

：1673-1379(2016)06-0594-07

10.3969/j.issn.1673-1379.2016.06.004

徐舒寒（1991—），女，硕士研究生，研究方向为振动隔离主动控制；E-mail: xushuhan@buaa.edu.cn。指导教师：黄 海（1963—），男，博士学位，教授，研究方向为飞行器结构优化，空间智能结构及其控制等；E-mail: hhuang@buaa.edu.cn。

2016-08-03；

：2016-11-11