激励频段对航天器随机振动载荷的影响

杨新峰，辛 强，单悌磊，邹轶群，扈勇强

（航天东方红卫星有限公司，北京 100094）

激励频段对航天器随机振动载荷的影响

杨新峰，辛 强，单悌磊，邹轶群，扈勇强

（航天东方红卫星有限公司，北京 100094）

在航天器随机振动等效准静态载荷计算中，高频因对随机振动载荷的贡献较小而可以被截去，但目前截止频率的选择还未有完全确定。为确定随机振动环境下的计算频段，文章设计了不同动态特性的组件进行不同截止频率的随机振动试验，并根据试验数据分析研究了不同特性组件在不同振动频段下应变的变化规律。研究结果认为，对于一般组件，随机振动的计算截止频率可取为组件主频率的 1.5倍。针对非均匀输入加速度谱的随机振动载荷计算问题，文章提出分频段的分析方法。按3个基本频段计算随机振动载荷，分析得到了不同频段对总随机振动载荷贡献大小和规律，以及截止频率误差的影响因素和影响大小。算例表明，分频段法可以用于不同状态输入加速度谱的随机振动载荷计算。

随机振动；准静态加速度；主频率；截止频率

0 引言

随机振动是航天器经历的一种重要的力学环境，主要产生自火箭整流罩外的气动噪声和发动机燃烧不稳定产生的推力脉动。在随机振动环境下，航天器及其设备的结构强度载荷设计依据主要是由随机振动环境等效转化而来的准静态加速度载荷。

Miles[1]最早就随机振动环境等效为准静态加速度载荷进行研究，并提出把随机振动动态载荷转化为准静态加速度载荷的 Miles公式：，其中为最大随机振动准静态加速度，fi为系统主频率，S(fi)为加速度输入谱在fi处的值，Qi为动态放大因子（Qi=1/(2ξ)，ξ为模态阻尼比）。Miles方法主要针对单一主模态结构，基于加速度输入谱（假定全频段均匀谱）计算随机振动加速度载荷。对一般多模态结构来说，它计算得到的载荷较为保守[2]。因此，对多模态结构，在Miles方法的基础上提出了模态质量参与法[3]，即把每个模态的Miles算法的结果按模态质量参与的比例求和，实际上是Miles方法的推广。Miles方法以及基于Miles的推广方法都是假定输入谱为全频段均匀谱（或白噪声谱），而实际上航天器随机振动环境一般为非均匀谱，如大多数航天器随机振动试验都是采取下凹的随机振动激励或者窄带的随机振动激励，这些还不能直接采用基于Miles的方法进行随机振动载荷计算。

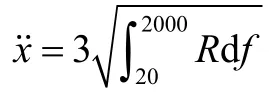
为分析振动频率对随机振动环境下总体载荷大小的影响，并确定计算的截止频率，本文利用试验数据开展激励频率对随机振动载荷的影响规律研究。为适应非均匀加速度输入谱下的随机振动载荷计算，采用分频段的方法对不同频段的随机振动载荷进行分析和研究。

1 研究方法

为了研究随机振动响应与激励载荷频段以及结构模态特性的关系，本文参考卫星常见的星上设备形式，设计了几种不同模态频率的铝合金结构组件，正弦扫描测试得到这些结构组件的主频率见表1。

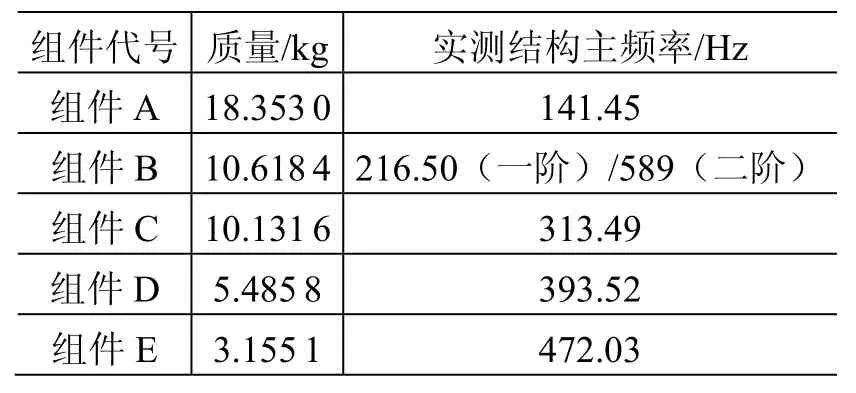
表1 不同组件实测结构主频率Table 1 Measured main frequencies for different assemblies

对上述组件，按照相同功率谱大小、不同截止频段（20～200 Hz、20～300 Hz、20～400 Hz、20～500 Hz、20～600 Hz、20～2000 Hz）的随机谱激励条件分别进行随机振动试验，每个频点的输入加速度功率谱见表2，其中20～2000 Hz频段定义为全频段。

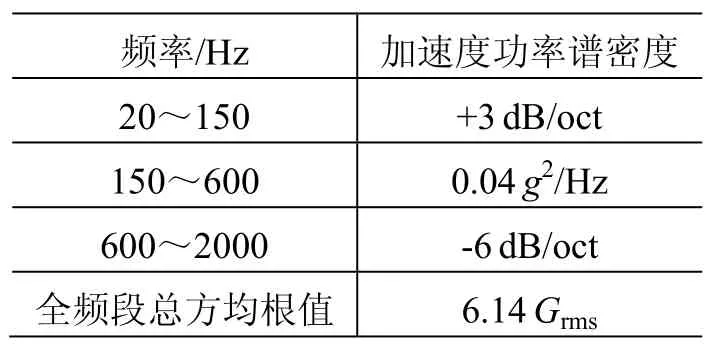
表2 随机振动试验输入加速度功率谱密度Table 2 Acceleration power spectrum density (PSD) input for random vibration test

试验过程中采集组件的加速度和应变的响应数据。应变测点和加速度传感器测点在组件根部。根据测试得到的不同频段的响应数据，分析各频段对随机振动载荷大小的影响，从而确定随机振动载荷计算截止频率。

2 激励频段的影响分析以及截止频率的确定

随机振动时引起组件纵向（定义为z向）应变最大，不同激励频段试验中测试得到的各组件z向应变大小见表3，其中应变响应方均根的量纲为1。可以看到随着激励频率频段的提高，应变响应总方均根的大小越发接近全频段的应变响应方均根大小，但趋近全频段总方均根的规律不一样：主频率较低的组件如组件A，在低频段已经有较大的应变方均根值（20～200 Hz频段已达到32.70）；而主频率较高的组件如组件E，低频段应变方均根较小，到一定的高频后（即20～500 Hz）才接近全频段总方均根。可见组件的主频率越低，其应变方均根越快趋近于全频段总方均根。

每一频段的应变方均根占全频段应变总方均根的百分比见表4。表中数据表明：主频率较高的组件如组件E，需要较宽频段才能达到较高的百分比，比波音公司研究人员提出的20～300 Hz频段要宽。若统一按波音公司的300 Hz作为结构设计载荷的计算截止频率，那么计算得到的等效加速度载荷偏小（如组件E在300 Hz以内只有9.62%），对于组件结构并不完全适用。

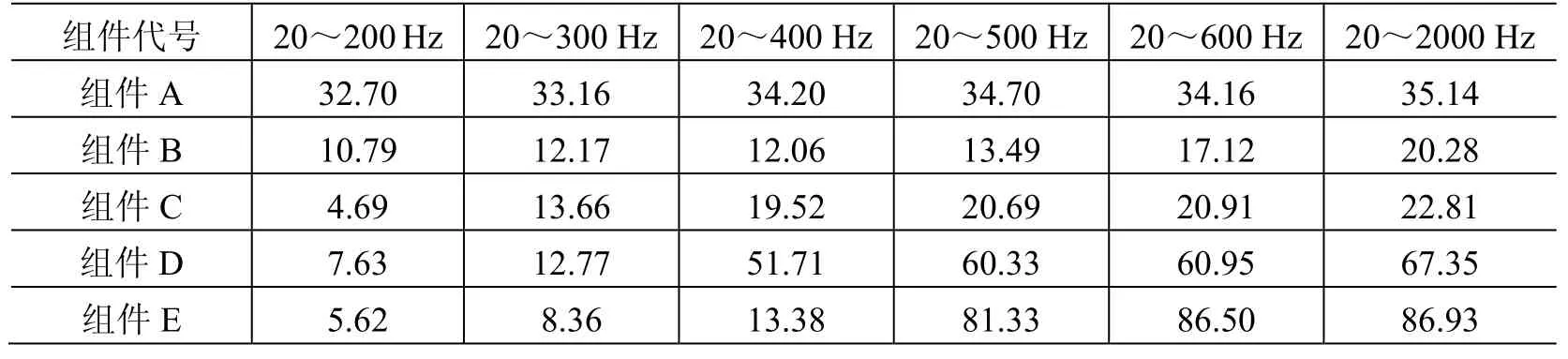
表3 各组件在不同频段激励下的应变响应方均根Table 3 Strain response RMS for different assemblies under different excitation bands ×10-6

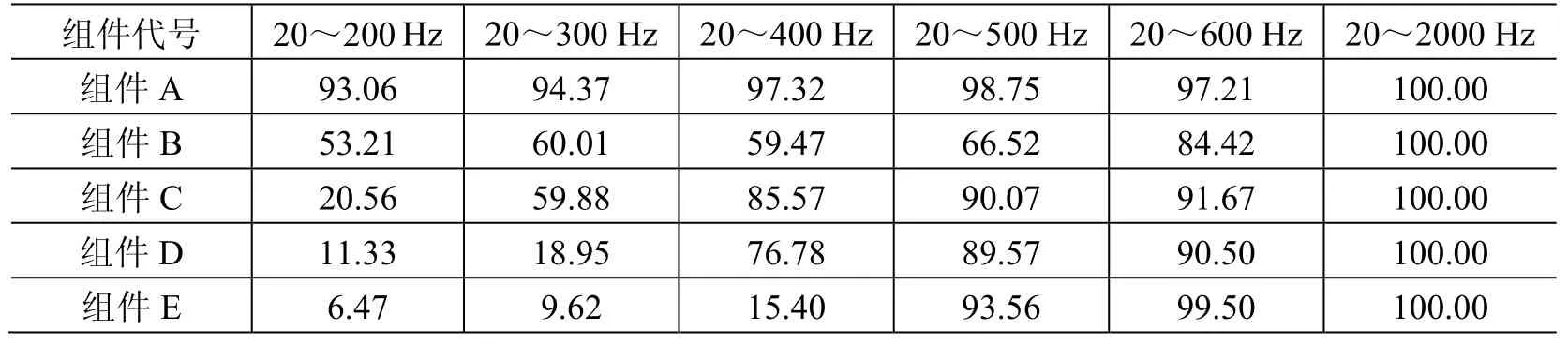
表4 各组件在不同频段激励下的应变响应方均根占全频段的百分比Table 4 Percentage of strain response RMS of different excitation bands over that of full frequency band for different assemblies %

对一个组件，不同频段的应变功率谱对总方均根贡献不同。以组件A和组件E为例，其应变功率谱密度见图1和图2。可以看到功率谱的贡献主要集中在共振频率及附近。

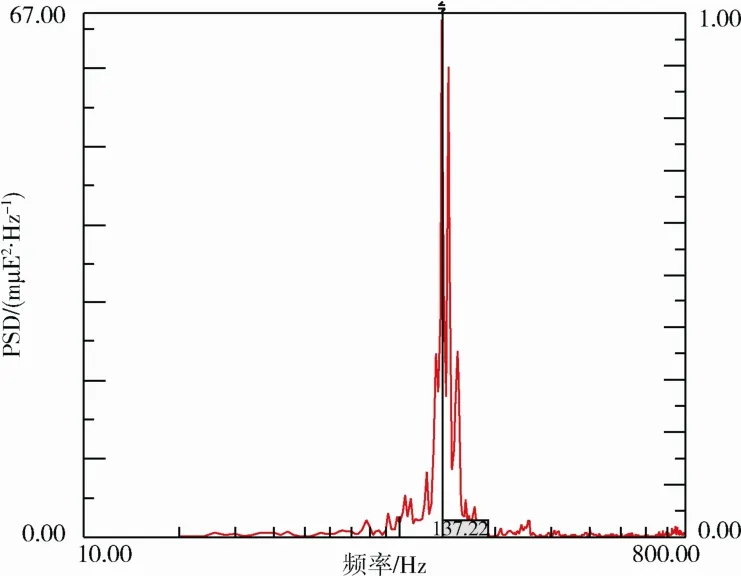
图1 组件A应变功率谱密度Fig.1 Strain PSD for assembly A

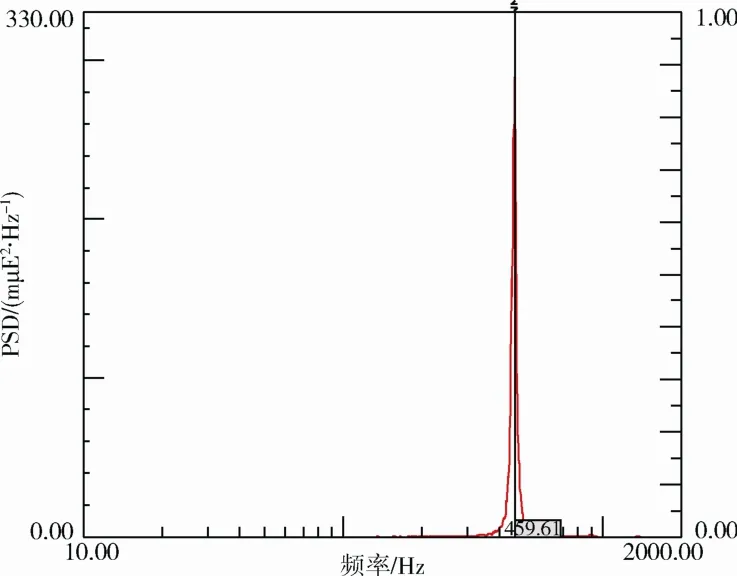
图2 组件E应变功率谱密度Fig.2 Strain PSD for assembly E

对于组件 A，最大应变功率谱发生在 137 Hz附近，对应于其一阶主频率（正弦低量级扫频得到的主频为 141.45 Hz，而随机大量级试验测试的峰值频率一般低于正弦低量级扫频得到的结果）。对于组件E，最大应变功率谱发生在459 Hz附近，也对应于其一阶主频率。可见，频段对应变方均根的影响与组件的主频率相关，产生影响的频段为包含主频率的一定范围的频段。这个频段随组件的主频率的变化而变化：当组件主频率提高，对随机振动产生主要作用的频段的高频端相应提高。

以主频率的1.5倍作为截止频率统计的应变方均根见表5，可以看到不同组件的方均根与全频段总方均根的占比在90%以上，基本上可以代表全频段的随机振动作用力。因此，产生主要作用力的频段不是一个固定的频段，是随组件的主频率而变化，大约至1.5倍主频率的一个频段。

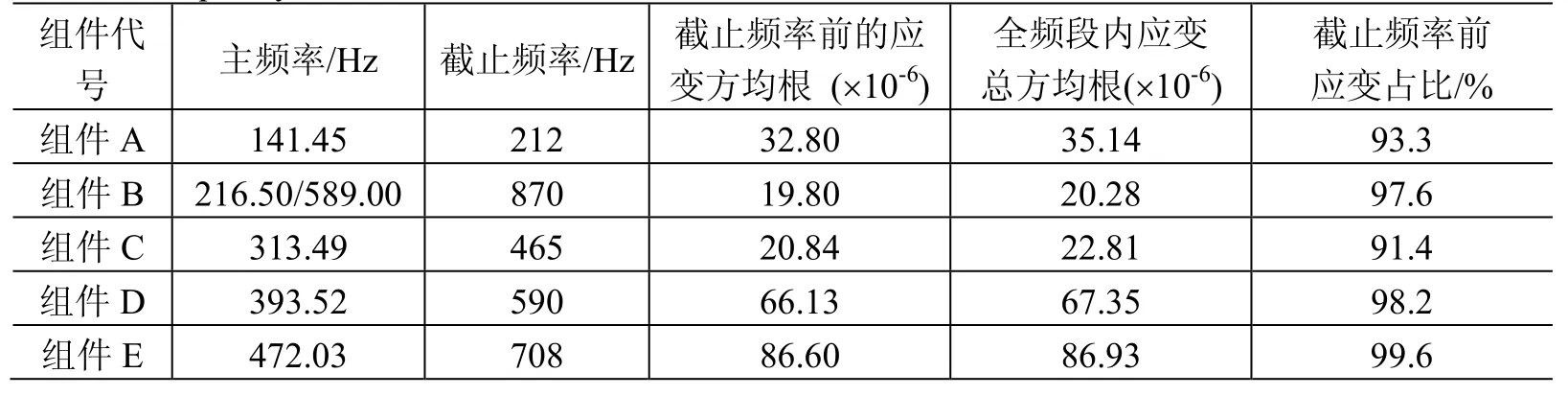
表5 主频率1.5倍为截止频率的应变方均根及其占全频段总方均根的比例Table 5 Percentage of strain response RMS of frequency band with cut-off frequency being 1.5 times of the main frequency over that of full frequency band for different assemblies

定义fn为组件的主频率或共振频率，基于上述分析，本文认为取20 Hz～1.5fn为随机振动力的计算频段较为合适。而目前文献中建议的截止频率300 Hz可能只适用于主频率不大于200 Hz的组件，并不适于所有组件。

对于多数组件，主频率就是其一阶主频即基频，如本文的组件A、组件C、组件D与组件E，因此组件截止频率考虑到一阶主频的1.5倍即可。如果组件主频率不是一阶主频，那一般将其二阶主频作为组件主频率，因此只需考虑到二阶频率的1.5倍，如组件B的主频率为二阶频率589 Hz，则截止频率为870 Hz。

3 不同频段的理论分析

当不能测试得到或不能精确仿真分析得到随机振动响应谱时，航天器及其设备的随机振动准静态载荷计算还是使用加速度输入谱。但当前的基于加速度输入谱方法（即Miles方法及其推广方法）是假定输入谱为均匀平直谱，为适应航天器中经常见到的非均匀输入谱，本节按分频段的方法进行分析。

单自由度系统（或单一主模态结构）由于相对简单，故作为分析的对象。对单自由度系统，先分析随机振动的加速度输入谱在不同频段的随机振动系统上应变的主要规律。

根据系统动态特性，可以把分析频段划分为共振频段、共振前频段和共振后频段。

3.1 共振频段

对于受基础激励振动的系统，假设S为基础激励的输入加速度功率谱密度，R为加速度响应功率谱密度，ω为振动频率（ω=2πf），ξ为阻尼比，ωn为系统主频率（ωn=2πfn）。则有[5]

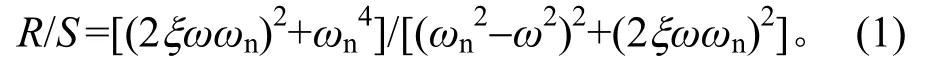
共振区域的随机振动加速度方均根计算需要确定2个参数：放大倍数（即加速度响应曲线在共振频率处的高度）和共振区域带宽。确定了这2个参数后，可以近似用三角面积公式表示共振区域的加速度载荷。

Sn为共振处输入加速度功率谱密度，根据式(1)，共振处（ω=ωn）的随机振动加速度响应为

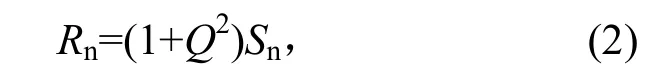
其中Q=1/(2ξ)。可见共振频率处随机振动加速度响应谱密度放大倍数为1+Q2。

共振区域的带宽可根据组件的实测应变响应数据来确定。组件D在均匀随机振动谱（0.04g2/Hz）输入下的实测应变曲线见图3所示。用三角面积公式Sa= (Δf×h/2)0.5近似计算共振区域的应变方均根，其中，h为峰值，Δf为带宽，图中应变曲线峰值h=126.67。同时，对应Δf带宽内的应变方均根可以从测量曲线积分获得。一定带宽的应变响应方均根测量值和近似三角公式计算值比较见表6。

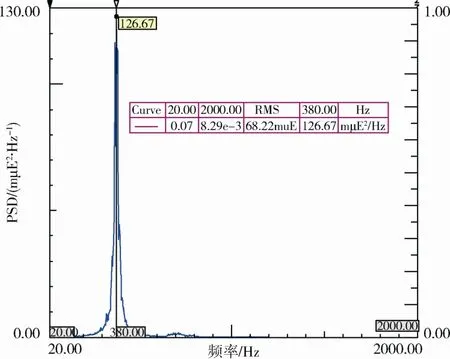
图3 组件D应变曲线Fig.3 Strain response curve for assembly D

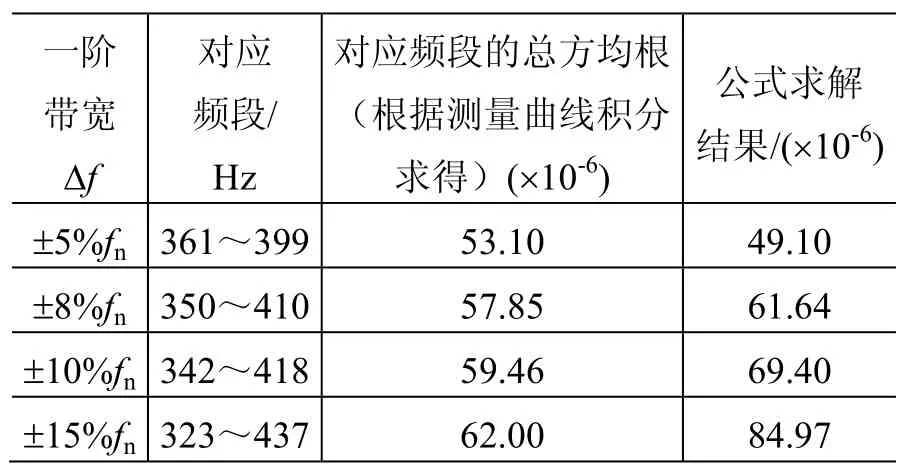
表6 组件D主模态的应变方均根比较Table 6 Comparisons between measured strain RMS and calculated strain RMS for assembly D

根据表6，带宽Δf大约取一阶频率的±8%作为计算值，这与测量值接近，因此取共振区域的计算带宽为Δf= 0.16fn。

基于共振处放大倍数和带宽，共振区域的等效振动加速度载荷可用近似公式表示为

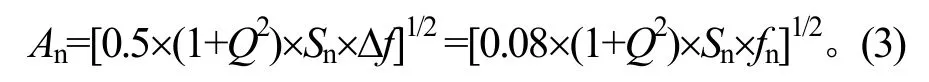
3.2 共振频率之前频段

在确定0.16fn带宽作为共振频段之后，共振频率之前频段即为0.92fn之前的频段。在共振频率之前，阻尼影响可以忽略，则有

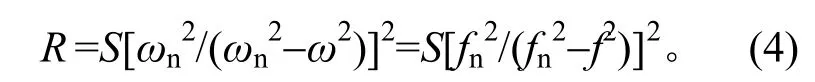
因此，在共振频率之前的总随机振动加速度方均根为

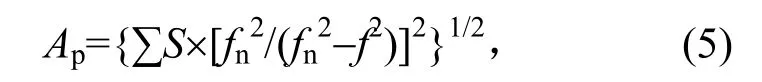
其中：fn为系统共振频率；f取值范围为f0～0.92fn。f0为最低输入激励频率，一般卫星随机振动试验中，f0为20 Hz。

3.3 共振频率之后频段

由于一般随机振动加速度试验的最高频率为2000 Hz，所以共振频率之后的频段f定义为1.08fn～2000 Hz。与共振之前频段类似，共振之后的频段总随机振动加速度为

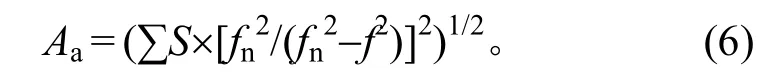
根据前述结论，1.5fn的截止频率之后的频率影响可以忽略，因此，f取值范围可为1.08fn～1.5fn。

3.4 全频段的加速度计算公式

根据上述划分的3个频段的加速度计算公式，可以得到总的全频段随机振动加速度载荷方均根为

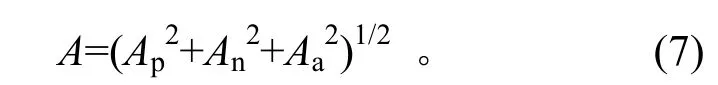
本文把式(7)简称为三频段计算公式。以100、200、300、400、500 Hz的5个不同主频率的系统分别在0.04g2/Hz加速度输入谱下进行振动为例，使用三频段公式计算随机振动加速度载荷，其结果与Miles公式计算结果（只取方均根即不乘3）的比较见表7。为与Miles公式计算结果比较，这里三频段计算公式中最低频率取为1 Hz，最高为2000 Hz，放大因子Q=10。

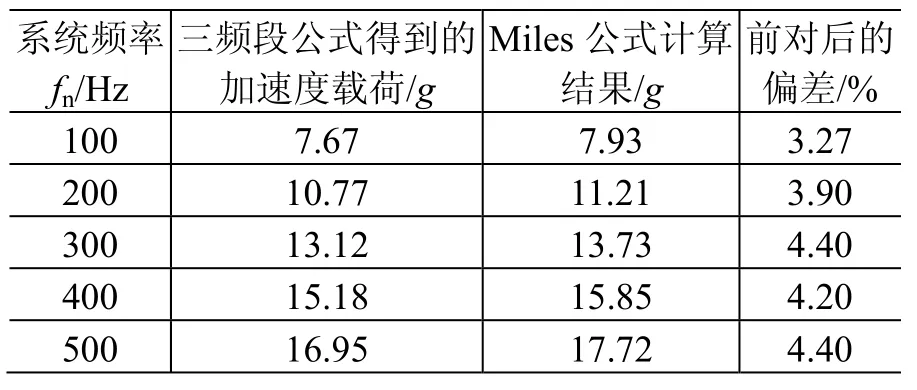
表7 三频段公式计算结果与Miles公式计算结果比较Table 7 Comparisons between tri-band formula results and Miles formula results

由表 7可以看到，三频段公式的计算结果与Miles公式的相比偏差较小，而且结果的变化规律接近，这验证了三频段公式计算的可信性。三频段公式不仅可以计算单自由度系统（或单一主模态结构）的加速度载荷，而且可以分析不同频段的影响、计算窄带随机振动载荷以及进一步用于多模态结构的加速度载荷分解计算。

当最高频率分别取2000 Hz和1.5fn时，三频段公式计算结果对比见表8，表中的加速度载荷为方均根值。

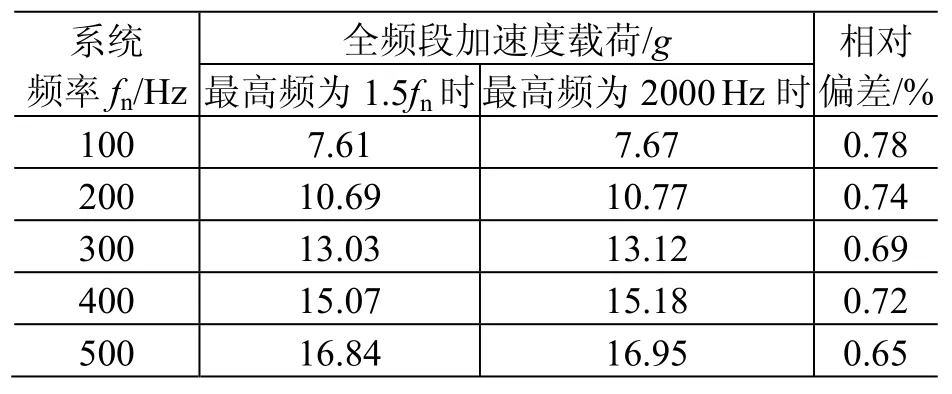
表8 两种频段的加速度载荷比较Table 8 Acceleration load comparisons for two different frequency bands

由表8可以看到：二者计算结果比较接近，相对偏差不超过0.8%，这也验证了随机振动截止频率取至1.5fn的合理性。

3.5 不同频段的对比分析

根据三频段公式，可以用上述分频段方法研究单自由度系统的共振区域和非共振段的加速度载荷大小。仍以系统固有频率分别为100、200、300、400、500 Hz的振动系统为例，其输入功率谱0.04g2/Hz，放大因子10，计算得到不同频段的加速度载荷见表9。由表9可以看到：共振频段的加速度载荷最大，其次为共振前频段，最小为共振后频段。3个频段的加速度载荷与全频段的占比见表10。表9和表10中加速度载荷为方均根值。

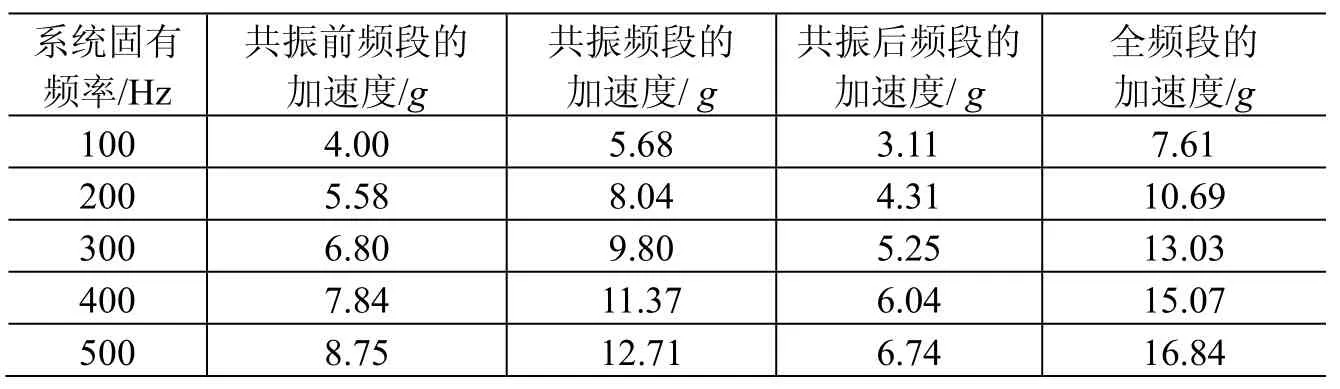
表9 不同频段随机振动加速度载荷Table 9 Random vibration acceleration loads for different frequency bands

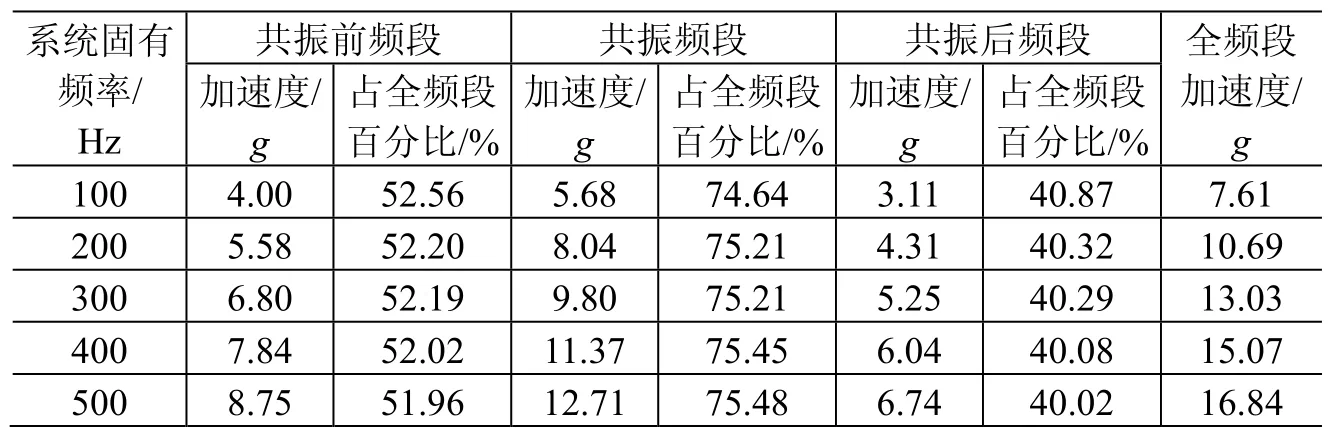
表10 三个频段加速度载荷所占百分比Table 10 Percentages of random vibration acceleration loads for three frequency bands

根据表10中数据，共振前频段、共振频段和共振后频段的加速度载荷分别约占全频段的52%、75%和40%。因为是方均根的关系，3个频段的加速度方均根百分比的平方和大约为1。不论系统频率高低，共振频段的加速度载荷所占全频段的比例基本不变，共振前频段和共振后频段也具有同样的规律。

上述计算是基于 3个频段的输入量级相同，即0.04g2/Hz的均匀谱。而对于非均匀加速度输入谱，即意味着从低频到高频可有不同量级的输入谱值，因此，可以参照三频段方法，即把非均匀加速度输入谱分为若干频段，把每个量级作为一个频段，如此一来每个频段内就是均匀输入谱的问题，再对这些均匀输入谱的频段求出各自的加速度方均根值，最后求和得到总的准静态加速度载荷。

3.6 多模态结构的频段对比分析

航天器结构及其设备多为多模态结构，即有多个共振频率，一般一阶共振频率（fn1）的模态质量比较大。对于多模态结构，共振前频段则定义为一阶共振之前，即小于0.92fn1的频段。在此频段，全部模态质量参与加速度载荷等效。共振前频段的加速度载荷方均根为

共振频段则包含多个共振峰，每个共振峰以及共振后频段的加速度载荷计算方法与单自由度振动系统类似；但由于每个共振区域并非全部模态质量参与，故每阶共振的加速度载荷按每阶模态质量比参与计算。第i阶共振与共振后的加速度载荷方均根分别为

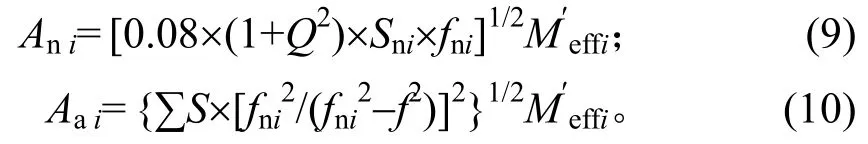
其中M′effi为第i阶模态质量比。因此，多模态结构的总随机振动加速度载荷方均根为

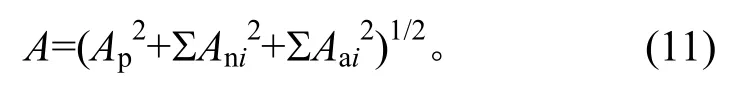
以弹簧-质量所构成的三自由度模型的三阶模态系统为例（取自文献[5]）进行分析对比，系统的3个质量m1=200 kg，m2=250 kg，m3=300 kg；3个弹簧刚度k1=108N/m，k2=2×108N/m，k3=3× 108N/m。该系统受基础激励，激励加速度输入谱S= 0.01g2/Hz，放大因子Q=10。文中计算给出三阶模态的频率为fn1=69.6 Hz，fn2=153.8 Hz，fn3=238.3 Hz；三阶模态质量比M′eff1=80.3%，M′eff2=14.9%，M′eff3=4.8%；系统加速度载荷力为20 377 N。根据三阶模态频率和模态质量比，使用三频段法对系统进行计算得到加速度载荷总方均根为2.777g，乘以总质量750 kg换算得到加速度载荷力为20 411 N。2种加速度载荷力计算结果相差约0.17%，说明三频段法计算多模态结构加速度载荷的正确性。

按照1.5fn1作为截止频率，一般情况下有限频段法中的积分频段只包含一阶共振频段和一阶共振后频段，如对于上述弹簧-质量的三自由度系统，1.5fn1的截止频率为105 Hz，相当于三频段法只计算一阶频率。若该系统按一阶模态（忽略其他两阶）并使用三频段法计算随机振动加速度载荷，得到加速度载荷力为19 860 N，与20 377 N相差2.5%，此误差是忽略二阶、三阶模态质量引起的。可以看出，多模态结构的截止频率计算误差与模态质量相关。针对三阶模态系统，保留一阶模态质量比约80%（即忽略二阶和三阶的20%）进行计算，结果相差还是比较小的。若一阶模态质量比取为70%，忽略其余30%模态质量，计算得到加速度载荷力为18 276 N，相差约为10%。因此，使用1.5fn1的截止频率计算随机振动加速度载荷时，还必须要求一阶模态质量比大于 70%，否则计算结果的误差较大。若一阶模态质量比小于70%时，唯有提高截止频率才能保证足够的计算精度。由于常见航天器及设备的一阶模态质量一般占主导地位，有些甚至接近单一主模态结构，所以，对一般航天器及设备使用加速度响应谱计算随机振动载荷时，选取 1.5fn1的截止频率进行计算可以满足要求。

假设单自由度系统的主频率与三自由度振动系统的一阶共振频率相同，均为 69.6 Hz，加速度输入谱都为 0.01g2/Hz，以此进行对比研究。根据三频段公式，共振前频段的加速度载荷取决于一阶主频率、一阶共振前频段以及输入谱，由于二者一阶主频率、一阶共振前频段和输入谱相同，所以两个系统的共振前频段的加速度载荷相同，但全频段的加速度载荷却不一样，分别为2.909g和2.777g。将单自由度系统的100%模态质量比与三自由度系统分散的模态质量比（三阶分别 80.3%、14.9%、4.8%）对比发现，总随机振动加速度载荷随着模态质量分散而降低了。结果表明具有相同一阶主频率的三阶模态结构与单一模态结构相比，共振前频段贡献相同，共振及共振后频段贡献减小了。同时也说明用针对单一模态结构的Miles方法计算多模态结构的随机振动载荷会偏大、偏保守。

4 结束语

分析结果表明，当前随机振动载荷计算中以300 Hz作为截止频率只适用于部分结构组件。截止频率的选取不仅应考虑结构主频率，而且还要考虑模态质量比。对于一阶模态质量比大于70%的航天器及设备组件，截止频率可取为组件主频率的1.5倍。

三频段分析法不仅可以用于随机振动加速度载荷的计算，而且还可以分频段分析不同频段的影响以及不同截止频率的计算误差。对于单模态结构，3个频段对加速度总方均根的贡献比例相对不变（52%，75%，40%）；而对于多模态结构，共振前频段的加速度方均根占比与单模态结构的相同，但共振及共振后频段的贡献减小，贡献比例随模态质量比变化而变化。

（

）

[1]MILES J W.On structural fatigue under randomloading[J].J of Aerospace Science, 1954, 21(11): 753-762

[2]LEE H M.Testing for random limit load versus static limit load: NASA technical memorandum 108542[R], 1997-09

[3]SURYANARAYAN S, KRISHNA M.Improved estimation of random vibration loads in launch vehicles[J].AIAA Journal,1993, 1092: 1-29

[4]CHUNG Y T, KREBS D J, PEEBLES J H．Estimation of payload random vibration loads for proper structure design[C]∥Proceedings of 42ndStructures, Structural Dynamics and Materials Conference and Exhibit.Washington D C: AIAA, 2001: 1667-1675

[5]航天器电子设备抗力学环境设计准则: Q/W 1227－2009[S]

[6]LEUNG K, FOIST B L.Prediction of acoustically induced random vibration loads for shuttle payloads[C]//Proceedings of 36thStructures, Structural Dynamics and Materials Conference and Exhibit.Washington D C: AIAA, 1995: 1200-1208

[7]WIJKER J.Random vibrations in spacecraft structures design[M].New York: Springer, 2009: 161-167

[8]邹元杰.基础激励和声激励下的设计载荷估算方法[C]//结构动力学会议.北京: 中国振动工程学会, 2009: 93-101

[9]杨宝宁.随机振动条件下设计载荷的确定[J].航天器工程, 2006, 15(3): 33-37 YANG B N．Engineering methods for determining quasi-static limit load for structures under random vibration[J].Spacecraft Engineering, 2006, 15(3): 33-37

[10]张玉梅, 韩增尧, 刘绍奎.航天器随机振动设计载荷比较[J].中国空间科学技术, 2013, 33(2): 7-12 ZHANG Y M, HAN Z Y, LIU S K.Comparisons of design loads under random vibration for spacecraft[J].Chinese Space Science and Technology, 2013, 33(2): 7-12

（编辑：肖福根）

The influence of frequency on the random vibration load of spacecraft

YANG Xinfeng, XIN Qiang, SHAN Tilei, ZOU Yiqun, HU Yongqiang
(DFH Satellite Co.Ltd., Beijing 100094, China)

For the quasi-static load computation of spacecraft under random vibration environment, the part of high frequencies contributes little to the random vibration load and could be cut off in computations.However, the selection of the cut-off frequency has to be determined.For that purpose, the assemblies with different dynamic characteristics are designed, and the random vibration tests are carried out on the assemblies with different cut-off frequencies.Based on the test data, the variations of the strain of the assemblies in different excitation frequency bands are analyzed.It is shown that, for general assemblies, the cut-off computation frequency is supposed to be 1.5 times of the main frequency of the assembly.For the uneven acceleration power spectrum input, we have no direct computation method, therefore, the frequency band method is proposed to calculate the random vibration load, and the contributions from different frequencies are analyzed, to determine the influencing factors of the cut-off frequency.The computation example indicates that the frequency band method could be used to correctly calculate the random vibration load.

random vibration; quasi-static acceleration; main frequency; cut-off frequency

0324

：A

：1673-1379(2016)06-0581-08

10.3969/j.issn.1673-1379.2016.06.002

杨新峰（1966—），男，博士学位，研究员，主要从事卫星动力学分析、大型试验、卫星减振、微振动分析与控制等工作。E-mail: stephenyang66@hotmail.com。

2016-11-11；

：2016-11-23

总装备部“十二五”星箭可靠性项目工程