锚栓限位与邻梁碰撞对曲线桥梁抗震性能的影响

焦驰宇， 肖 翔， 龙佩恒， 徐 艳， 侯苏伟， 张 羽

(1.北京建筑大学 北京市城市交通基础设施建设工程技术研究中心,北京 100044；2.北京建筑大学 北京节能减排关键技术协同创新中心,北京 100044； 3.同济大学 土木工程防灾国家重点实验室,上海 200092)

锚栓限位与邻梁碰撞对曲线桥梁抗震性能的影响

焦驰宇1,3， 肖 翔1， 龙佩恒2,， 徐 艳3， 侯苏伟2， 张 羽1

(1.北京建筑大学 北京市城市交通基础设施建设工程技术研究中心,北京 100044；2.北京建筑大学 北京节能减排关键技术协同创新中心,北京 100044； 3.同济大学 土木工程防灾国家重点实验室,上海 200092)

曲线桥梁在地震作用下梁体之间会发生非均匀碰撞，可能造成前梁落梁或后梁局部破坏现象;而在纵向设置抗震锚栓可有效防止落梁，也可对相邻梁的碰撞起到一定缓解作用;但目前国内外还缺乏锚栓对曲线桥梁的抗震性能影响的相关研究。以某四跨曲线桥为背景工程，建立了空间有限元模型，并分别用滞后系统、钩单元、接触单元模拟了支座损伤、锚栓约束、相邻梁纵向碰撞等物理现象，利用非线性时程分析法，进行了三种工况(①无锚栓、不计碰撞，②无锚栓、计碰撞，③有锚栓、计碰撞)曲线桥梁的墩梁相对位移、墩底内力、相邻梁碰撞力等关键地震响应对比研究。研究表明：相邻梁的非均匀碰撞是曲线桥梁必须考虑的关键因素；而设置抗震锚栓能缓解曲线桥梁的碰撞效应，并减轻震害。

曲线桥梁；相邻联碰撞；抗震锚栓；抗震性能

曲线桥在地震作用下的倒塌破坏多与相邻主梁间的碰撞现象有关，又因为曲线桥几何非规则性，在地震中碰撞现象时有发生。在此方面，自20世纪70年代以来，国内外学者开展了广泛的研究。1971年，TSENG等[1-2]采用数值模拟方法，建立了能考虑碰撞、屈服的伸缩缝力学模型，解释了SAN FERNANDO地震中曲线桥的震害原因；1979年，WILLIAMS等[3]建立了大跨钢筋混凝土曲线梁的1/30缩尺模型进行对比分析，揭示了碰撞是导致落梁的主要原因；21世纪以来，国内学者王东升等[4-5],SCHIEHLEN等[6],岳福青等[7]通过研究，提出了KELVIN碰撞模型及其参数确定方法，为分析碰撞对地震反应的影响奠定了基础。此后，王军文等[8]将直杆共轴碰撞模型、KELVIN模型等用于对直线简支梁桥、连续梁桥、非规则桥梁的碰撞分析当中，推荐了非规则梁桥纵向、横向碰撞的数值模拟方法。然而，曲杆毕竟与直杆几何形式不同，因此，吴璟[9]研究了曲杆轴心碰撞理论，由于其仅考虑了曲杆沿杆端平动的情况，其结论表明：仍可采用KELVIN模型分析曲线梁的梁端碰撞，但其碰撞刚度应修正为较短主梁的轴向刚度。此后，注意到曲线桥梁地震中出现不规则的平面转动使碰撞力分布不均、碰撞部位不明确，亓兴军等[10]及胥强[11]提出采用显式动力接触算法进行曲线梁桥碰撞的模拟，并将该方法与固定接触面的接触单元法进行了对比。其研究表明：该方法能更加准确的用于无法判别接触位置的碰撞问题，但其存在计算过程太耗时，对网格划分要求高、对材料选取要求严格等弊端；此外柳国环等[12]发展了一种适用于体元模拟联间轴向正面碰撞效应的束缚面碰撞单元(Constraint Surface-Impact Element，CIE)，并基于柔度法给出了非线性碰撞单元刚度，通过试验得到双线性碰撞刚度，充分模拟了曲线梁的复杂碰撞行为，特别是梁端非均匀接触的行为。

国内外研究表明：碰撞往往引发前梁落梁和后梁损伤现象，因而在实际工程中，往往在梁体两侧加设挡块以防止梁体横向移位、在纵向设置钢锚栓(见图1)连接盖梁与墩柱，防止切向相对位移过大而发生的主梁落梁现象。目前，国内外学者对碰撞和锚栓在桥梁抗震中的研究多数以直线桥为背景[13]，还缺乏抗震锚栓对曲线桥梁的抗震性能影响。本文以一座曲线桥梁为背景，在考虑非均匀碰撞的基础上，探讨抗震锚栓对相邻联碰撞的影响，着力探查两种非线性行为对曲线桥关键地震反应的影响。

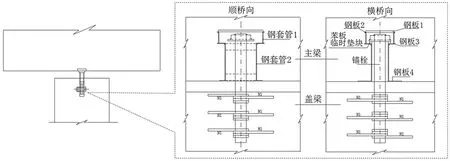
图1 锚栓示意图

1 建立模型

1.1 工程背景

北京某互通式立交桥中的G匝道桥长609.00 m、宽8.5 m，平曲线线型为缓和曲线和圆曲线交替。上部结构共分4联，第一联为现浇5×31 m预应力混凝土连续曲线箱梁，前28 m为R=480 m圆曲线，后段为A=150 m缓和曲线。第二联为现浇5×33 m预应力混凝土连续曲线箱梁，前57 m为A=150 m缓和曲线，后段为R=165 m圆曲线。第三联为40 m+40 m+42 m混凝土叠合连续曲线箱梁，全联为R=165 m圆曲线。第四联为现浇4×40 m预应力混凝土连续曲线箱梁，其中前37 m为R=165 m圆曲线，中段65 m为缓和曲线，后段为R=650 m圆曲线。下部为柱式墩台，两联连接处采用双柱墩，其余墩柱为单柱墩，钻孔灌注桩基础。全桥结构形式见图2，0#、17#为桥台，5#、10#、13#墩柱为连接墩。连接墩采用聚四氟乙烯滑板支座，中间墩采用抗震固定盆式支座。该桥在联与联之间设置了防撞挡块和抗震锚栓。

1.2 数值模拟

已有研究表明：使用MIDAS/CIVIL有限元模拟软件，对全桥建立有限元模型，可以考虑非线性影响获得对桥梁地震反应的详细认识。据此，本文建立了三维有限元模型，主梁顺桥向为X轴，横桥向为Y轴，竖向为Z轴，墩柱顺桥向为Y轴，横桥向为Z轴，竖向为X轴。由于桥宽较窄，主梁、墩柱、单桩采用三维空间梁单元模拟，沿桩身施加等代弹簧方式模拟桩侧土对单桩的弹性作用。

为获得真实的桥梁地震反应，需考虑构件之间复杂的非线性相互作用行为，在本例中，主要考虑了支座超过设计剪力后进入滑动状态的非线性力学行为、主梁与盖梁挡块间的横向碰撞行为、主梁与主梁间的碰撞行为、盖梁与主梁间的锚栓连接行为，各种连接的关系见图2。

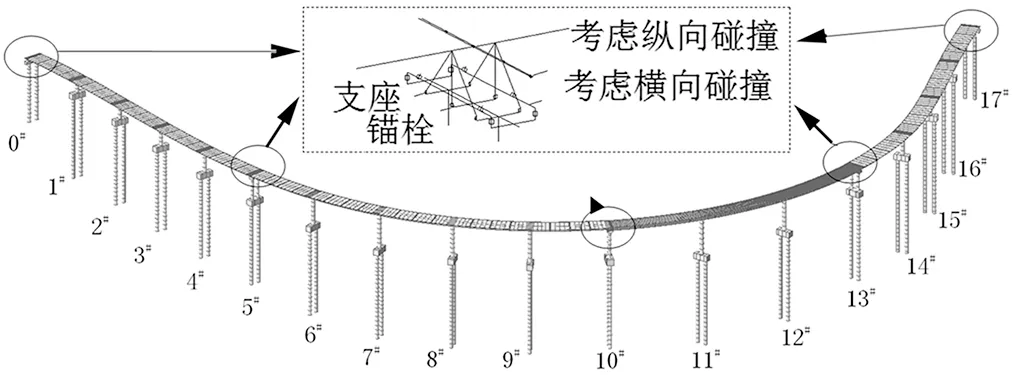
图2 北京某互通式立交桥中的G匝道桥(全桥)

1.2.1 支座模拟

该桥固定墩采用为抗震固定盆式支座，文献研究表明：在罕遇地震下，固定支座超过容许剪力时，可采用滑动摩擦耗能状态对非线性力学行为进行模拟。依据固定盆式支座的构造(见图3)考虑盆式支座相关参数(如橡胶材料参数，钢盆材料参数，接触碰撞条件)，建立ABAQUS模型见图4。虽然震害研究表明，盆式支座在地震中底盆会发生局部破坏，但已有研究表明[14]：盆底发生的细微局部破坏对盆式支座滞回曲线不造成显著影响。因此，本次分析中假定盆式支座主要震害仅发生在盆体内部，且底盆与主梁连接牢固，通过计算最终获得盆式支座的滞回曲线见图5。

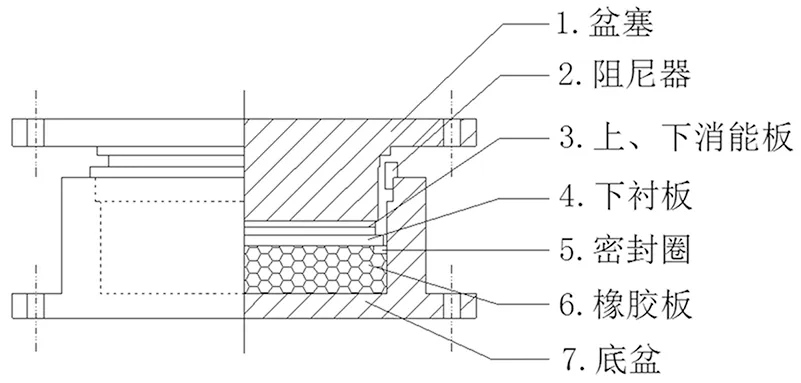
图3 抗震盆式支座结构构造示意图

图4 抗震盆式支座结构有限元模拟图

图5 抗震盆式支座滞回曲线

对图5进行分析可知，MIDAS/CIVIL软件中的滞后系统可以一定程度模拟固定支座超过容许剪力时的损伤后抗震性能(见图6)。

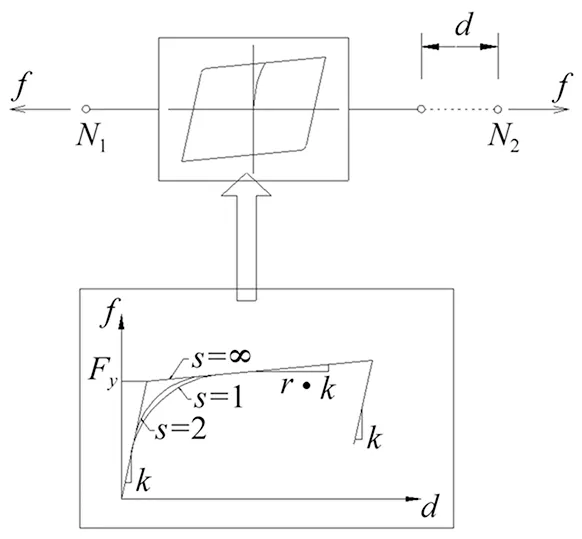
图6 支座模拟及本构关系

该单元的关系式为：

式中：k为弹性刚度;Fy为屈服强度;r为屈服后刚度和弹性刚度之比取值为0.001;s为屈服指数取值为50，α、β为滞后循环参数;︱α︱+︱β︱=1.0，分别取值α=0.5、β=0.5。本文所采用的曲线梁桥抗震支座为两种型号，弹性刚度k取值1 000 000 kN/m、1 250 000 kN/m，屈服强度Fy相应取为2 000 kN、2 500 kN。

过渡墩采用的聚四氟乙烯滑板支座模拟方法与固定墩的抗震固定盆式支座相似，但弹性刚度k与屈服强度Fy取值不同，弹性刚度k取值3 770～17 730 kN/m，屈服强度Fy为7.5～35.5 kN。

1.2.2 锚栓模拟

如锚栓构造图1所示，为了适应主梁在温度作用下纵横向的自由变形，锚栓与主梁之间并不是完全刚性连接，锚栓上部与主梁之间有一定的间隙。因此，地震运动中，只有消耗掉锚栓与盖梁之间的间隙后，锚栓才能通过自身弹性剪切变形将主梁惯性力传递给盖梁，从而起到限制主梁移位防止落梁的目的。目前国内外研究中没有锚栓与梁体连接关系的统一模拟方法。在此，根据锚栓与接触主梁之间的施工图，采用ABAQUS软件对锚栓与主梁间的连接关系进行细节模拟。锚栓模型示意图如图7所示：采用8节点实体单元划分上部几何体以模拟局部主梁碰撞位置，中部圆柱体模拟钢锚栓，下部几何实体模拟局部盖梁碰撞接触位置。按照实际尺寸模拟锚栓与主梁之间的空隙，并在其间设置接触单元(按照库伦接触理论考虑)，锚栓与盖梁固定采用实体单元固结模拟。在主梁接触面上施加移动荷载，预分析表明，地震中最大墩梁相对位移顺桥向不超过20 cm，横桥向不超过10 cm。

图7 锚栓有限元模型示意图

通过拟静力数值仿真分析，获得锚栓与主梁间的相对位移关系，可以发现钢锚栓的位移剪力曲线为线性关系，其横桥向位移剪力关系图如图8所示，当钢锚栓位移达到2.5 cm后与上部梁体发生接触，钢锚栓截面产生剪力。纵桥向位移剪力关系图如图9所示，当钢锚栓位移达到9 cm后与上部梁体接触，钢锚栓内部产生剪力。无论纵横向，其剪力与锚栓抗剪刚度均成正比。

图8 锚栓横桥向位移剪力关系图

图9 锚栓纵桥向位移剪力关系图

分析发现，抗震锚栓可采用MIDAS/CIVIL软件中的钩单元模拟(见图10)。

图10 锚栓模拟

该单元的关系式为：

(1)

1.2.3 碰撞模拟

现有文献表明：主梁与挡块之间的相互碰撞，采用接触单元模拟(见图11)。

图11 碰撞模拟

其关系式为：

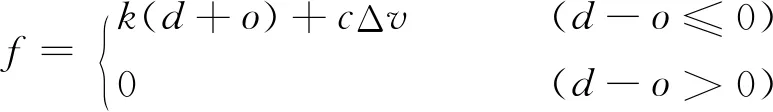
(2)

式中：d为N1、N2两点之间的相对位移;k为发生碰撞后间隙单元的轴向位移刚度;c为阻尼系数;Δv为相对速度。通过能量守恒定律可知阻尼系数c与恢复系数e的关系为：

(3)

(4)

横向碰撞中，k可取为挡块的抗弯刚度(考虑剪切变形影响)，本文中取k=1.17×107kN/m，挡块与盖梁间的初始间隙按实际间隙5 cm采用。横向碰撞模型见图12。

图12 横向碰撞模型图

1.3 地震波输入

该桥地处Ⅲ级场地，烈度为8度。利用罕遇地震下规范反应谱生成了7条人工地震波(其峰值为5.065 9 m/s2),加速度时程曲线如图13所示。由于第三联上部结构为钢-混凝土叠合梁，地震反应较大,控制全桥结构设计。因此，依据《08抗震细则》，地震波的输入方向取为第三联曲线梁的割线方向。

图13 人工地震波加速度与时间函数图

2 两种非线性现象对结构抗震性能影响

本文首先在考虑恒载的基础上对结构进行非线性时程反应分析，取7条时程波分析结果的平均值作为比较基础。本文主要对比三种工况，①没有考虑碰撞效应，也没有设置锚栓。②考虑了桥梁在地震作用下的碰撞效应，但仍未设置锚栓。③考虑了桥梁在地震作用下的碰撞效应，同时考虑了锚栓的设置。

已有研究表明：桥梁的墩柱将主梁的恒载及地震作用传递给基础，因而墩柱为地震中的核心受力构件，所以有必要研究地震作用下墩柱内力的影响。同时，地震中梁体会产生位移，墩柱也会受地震作用影响而产生位移，两者之间存在位移差，当位移差大于支承面宽度会导致落梁现象。因而对比分析中，墩梁相对位移也是重点关注因素。

2.1 非均匀碰撞现象

对于直线桥而言，桥梁地震作用中的碰撞可以近似为均匀碰撞。但对于曲线桥来说，曲线桥的几何形式与直线桥不同，曲线桥有曲率半径，可能会造成梁体在地震作用下发生不均匀的碰撞现象。

因而，在本研究中，每个梁体之间的纵向碰撞共设置了5个碰撞单元，如图14所示。从图14可知，曲率半径最小的碰撞单元为碰撞点1，依次向外排列，曲率半径最大的碰撞单元为碰撞点5。图15～图19为各碰撞点在有锚栓、有碰撞工况中，E2—1模拟地震波作用下的碰撞力，选取的是碰撞单元在地震作用下所受到接触力。

图14 碰撞单元示意图

图15 碰撞单元1碰撞力图

图16 碰撞单元2碰撞力图

图17 碰撞单元3碰撞力图

图18 碰撞单元4碰撞力图

图19 碰撞单元5碰撞力图

由图15～图19可知，5个碰撞点发生碰撞几乎都是在同时刻，只有第5次碰撞只发生在碰撞点1、碰撞点2上，说明当曲线桥由于主梁梁端曲率半径不同，沿梁宽地震中碰撞力时程趋势并不相同。所以对于曲线桥的碰撞研究，只在中间加一个碰撞单元是不可取的。在同时刻的碰撞中，各点的碰撞力均不相同，碰撞点1的碰撞力最大，碰撞点5最小。可以说明曲线桥相邻梁体间确实存在不均匀接触的碰撞现象，从分析发现主要呈现曲线梁内侧碰撞次数较多，碰撞力较大；而外侧碰撞次数少，碰撞力较小的规律。

2.1.1 碰撞对墩梁相对位移的影响

图20～图21为两种工况(有碰撞、无锚栓与无碰撞、无锚栓)的梁体相对墩柱位移图，分为切向墩梁接近相对位移、切向墩梁背离相对位移、径向墩梁相对位移。切向墩梁接近相对位移是指：在曲线切线方向，主梁与墩柱相对接近时产生的相对位移；切向背离相对墩柱位移指梁体与墩柱相背运动产生的相对位移。图中选取了2个节点，1号节点为第三联梁体左端节点，2号节点为第三联右端节点。

图20 两工况墩梁切向相对位移图

图21 两工况墩梁径向相对位移图

图中两种工况相对位移规律一致，但无碰撞工况的位移量比有碰撞位移量稍大。可以看出：有碰撞工况由于考虑了碰撞效应，梁体之间的相互碰撞阻碍了切向墩梁接近相对位移。而在本分析中，梁体碰撞时，对切向墩梁背离相对位移的影响不大。而在径向，与不考虑碰撞相比，碰撞使得径向墩梁相对位移减小。

2.1.2 碰撞对墩柱内力的影响

图22～图25为两种工况(有碰撞、无锚栓与无碰撞、无锚栓)墩柱内力图，包括切向剪力、径向剪力、切向弯矩、径向弯矩。选取了1号～16号桥墩;1号～5号桥墩为第一联，5号～10号桥墩为第二联，10号～13号桥墩为第三联，12号～16号桥墩为第四联。整体而言，离桥台最近的曲线桥墩第一联和第四联，墩底切向内力较大，墩底径向内力较小，而中部的第二联和第三联，墩底切向内力较小，墩底径向内力较大。造成这种现象的主要原因是：本次地震分析中，取第三联曲线梁的割线方向做为地震动的输入方向，而该桥有一定的曲率，第一联、第四联的切向和第二联、第三联的径向方向大致相同，所以造成这种现象。

图22 两工况墩底切向剪力图

图23 两工况墩底径向剪力图

图24 两工况墩底切向弯矩图

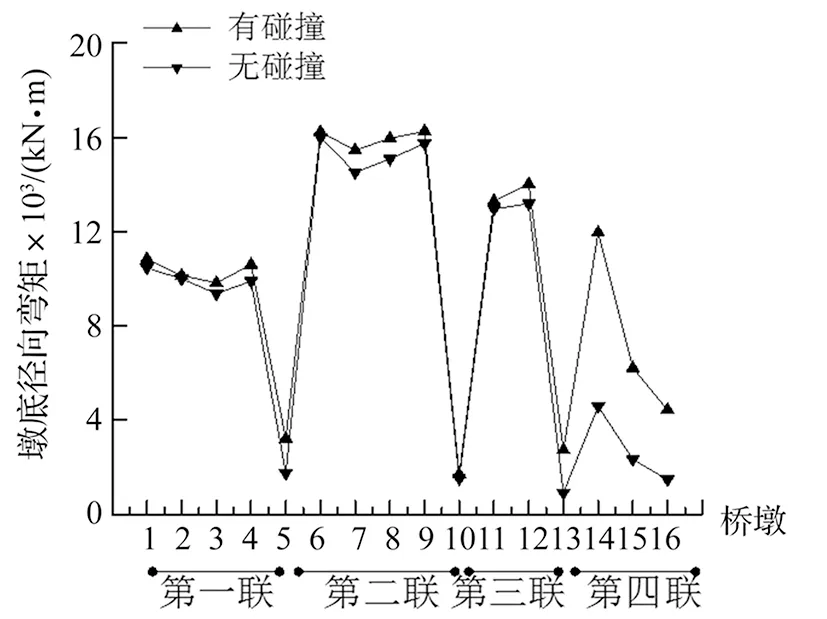
图25 两工况墩底径向弯矩图

从图22～图25可知，两种工况的四组墩柱内力值规律大体一致，但有碰撞、无锚栓工况的内力值比无碰撞、无锚栓工况的内力值大，且在第二联和第四联的区别最大。无碰撞、无锚栓工况没有考虑碰撞的影响，地震时梁体碰撞造成的内力没有被计入，所以无碰撞、无锚栓工况的墩柱内力较小。此前，邹立华等[15]分析得出碰撞与相邻结构周期有关，本案例第三联为钢筋预应力混凝土叠合连续曲线箱梁，其余三联为预应力混凝土连续曲线箱梁，以致四联的振动频率周期不同(梁体振动周期见表1)，故造成第二联和第四联考虑碰撞与未考虑碰撞的内力区别较大。

表1 计算模型振动周期汇总表

2.2 锚栓性能研究

为研究锚栓的限位的作用，选取了在E2-3地震波作用下在第二、第三跨之间第三跨上的59号锚栓为对象，研究其在地震作用下的位移。

为了比较锚栓的相对位移的大小，在有锚栓、有碰撞工况中，选取了锚栓单元的位移，在无锚栓、有碰撞工况中，在锚栓位置添加了一个节点，分析了该节点的相对位移。从图26～图27可知，无锚栓、有碰撞工况中切向位移最大幅值为0.283 m，径向最大幅值为0.227 m，有锚栓、有碰撞工况中，因为径向初始间隙为0.025 m，切向初始间隙为0.09 m，径向位移最大幅值为0.026 m，切向最大幅值为0.091 m。有锚栓、有碰撞工况的锚栓位移与无锚栓、有碰撞工况的锚栓位移相比，位移量明显小于无锚栓、有碰撞工况。所以，抗震锚栓在地震中能够非常有效地减小径向位移，限制梁体位移。

图26 锚栓切向位移图

图27 锚栓径向位移图

锚栓切向有很强的限位能力，原桥设计中为满足温度变形要求锚栓切向的允许位移量远大于径向位移量，因而切向与径向相比，发生较大的位移量时，才会限制相对位移。在抗震设计考虑锚栓与梁体的间隙时，需满足温度变形可适当取较小的间隙值，以限制更大的位移值。

2.2.1 锚栓对梁体相对墩柱位移的影响

图28～图29为三种工况(添加了有碰撞、有锚栓工况)梁体相对墩柱位移图，分为切向墩梁接近相对位移、切向墩梁背离相对位移、径向墩梁相对位移。图中选取了2个节点，1号节点为第三联梁体左端节点，2号节点为第三联右端节点。

图28 三工况梁体切向相对位移图

图29 三工况梁体径向相对位移图

从图28～图29可知，有锚栓、有碰撞工况的规律和前两种工况一致，且有锚栓、有碰撞工况的墩梁相对位移量最小，无锚栓、无碰撞工况相对位移最大，无锚栓、有碰撞工况相对位移量次小。在盖梁和墩柱之间用具有很大抗剪刚度的抗震锚栓连接，能够承受很大的剪力，具有很强的限位作用，能够限制结构在地震作用中梁体和墩柱的位移防止落梁，从图28知图29可知，当梁体切向运动相背离时，锚栓对梁体的限制效果更明显。

2.2.2 锚栓对墩柱内力的影响

图30～图33为三种工况(添加了有碰撞、有锚栓工况)墩柱内力图，包括切向剪力、径向剪力、切向弯矩、径向弯矩。选取了1号～16号桥墩，1号～5号桥墩为第一联，5号～10号桥墩为第二联，10号～13号桥墩为第三联，12号～16号桥墩为第四联。

图30 三工况墩底切向剪力图

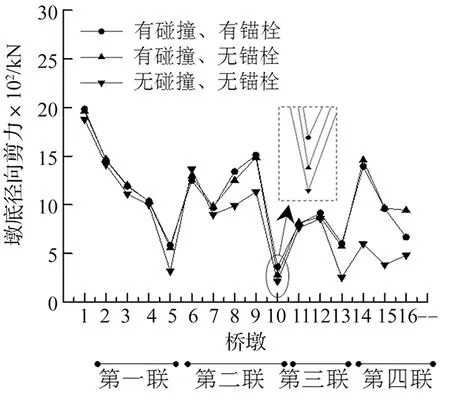
图31 三工况墩底径向剪力图

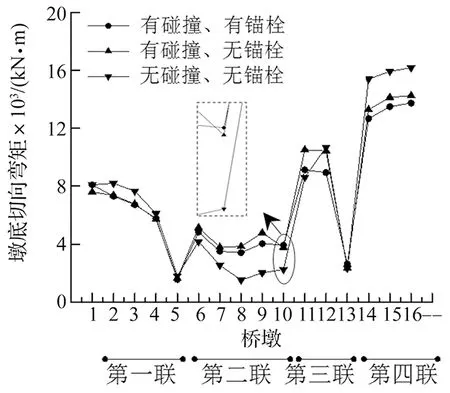
图32 三工况墩底切向弯矩图

图33 三工况墩底径向弯矩图

从图30～图33可知，有碰撞、有锚栓工况的规律和前两种工况大体一致，墩底剪力及弯矩值与有碰撞、无锚栓工况相比略有增大。有碰撞、有锚栓工况中设置了锚栓，锚栓可以把力传递到过渡墩上，使力分散更均匀，分担了一部分中间墩的反力，所以有碰撞、有锚栓工况的墩柱内力较均匀。但同时，由于过渡墩的聚四氟乙烯滑板支座仅传递摩擦力给过渡墩，因而过渡墩墩底内力量值较小，故锚栓增加的内力不明显。

3 结 论

本文研究锚栓和碰撞设置对曲线桥抗震性能的影响，以某四跨曲线桥为实际工程背景，构建了三个不同工况的模型，通过对三个模型在人工地震作用下的受力情况的对比研究，得到以下几个结论：

(1)地震作用下，曲线桥和直线桥不同，所以曲线桥的碰撞和直线桥的碰撞有所不同，表现出强烈的非均匀碰撞特征，且越靠近曲率中心，碰撞概率越高，碰撞力越大，并向外依次递减。对桥梁整体而言，曲率半径越小，非均匀碰撞现象越明显。

(2)曲线桥中的碰撞效应会阻碍梁体的移位，特别是在梁体运动相接近时，梁体位移会显著减小。

(3)锚栓连接在墩柱与梁体之间，可以有效的限制梁体的位移，特别是梁体发生切向运动相背离时的效果更明显，限制的最大位移量取决于锚栓与梁体之间的间隙。

(4)锚栓虽然会对墩梁的相对背离产生一定的约束作用，但也会部分增加墩柱的地震受力，所以在一联连续梁中设置锚栓的墩柱应在抗震分析中引起一定的重视。

[ 1 ] TSENG W S, PENZIEN J.Seismic analysis of long multiple-span highway bridges[J] Earthquake Engineering and structural dynamics, 1975, 4:3-24.

[ 2 ] TSENG W S, PENZIEN J.Seismic response of long multiple-span highway bridges[J] Earthquake Engineering and Structural Dynamics, 1975, 4:25-48.

[ 3 ] Williams D, Godden W, Experimental model studies on the seismic response of highcurved overcrossings[R]. Report No. 76/18, Earthquake Engineering Research Center University of California at Berkeley, June, 1979.

[ 4 ] 王东升, 冯启民, 王国新. 基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型[J]. 工程力学,2004, 21(2):157-166. WANG Dongsheng, FENG Qimin, WANG Guoxin. Analysis model of pounding between adjacent bridge girders during earthquakes based on collinear impact between rods[J]. Engineering Mechanics,2004, 21(2):157-166.

[ 5 ] 王东升, 王国新, 冯启民. 桥梁结构地震反应邻梁碰撞分析等效刚体模型[J].工程力学， 2004, 21(4):81-85. WANG Dongsheng, WANG Guoxin, FENG Qimin. Equivalent rigid-body compact model of pounding between adjacent bridge girders during earthquakes[J]. Engineering Mechanics， 2004, 21(4):81-85.

[ 6 ] SCHIEHLEN W, SEIFRIED R. Three approaches for elastodynamic contact inmultibody systems[J]. Multibody System Dynamics, 2004, 12(1):1-16.

[ 7 ] 岳福青. 地震作用下隔震高架桥梁的碰撞反应及控制[D].天津：天津大学建筑工程学院，2007.

[ 8 ] 王军文, 李建中, 范立础. 非规则梁桥伸缩缝处的碰撞对地震反应的影响[J].土木工程学报, 2006, 39(1):54-59. WANG Junwen, LI Jianzhong, FAN Lichu. Effect of pounding at expansion joints on seismic response ofirregular girder bridges[J]. China Civil Engineering Journal, 2006, 39(1):54-59.

[ 9 ] 吴璟. 隔震曲线桥梁碰撞研究[D].武汉:华中科技大学,2008.

[10] 亓兴军, 申永刚. 地震作用下曲线梁桥非均匀碰撞效应研究[J],振动与冲击, 2012,31(6):72-76. QI Xingjun, SHEN Yonggang. Uneven distribution of pounding effect in a curved girder bridge under earthquake[J]. Journal of Vibration and Shock, 2012,31(6):72-76.

[11] 胥强. 曲线连续梁桥地震碰撞分析与减碰方法[D].济南：山东建筑科技大学，2012.

[12] 柳国环, 李宏男, 陆新征. LRB曲线桥震致碰撞效应的非线性分析方法[J].土木建筑与环境工程，2012(5)：17-24. LIU Guohuan, LI Hongnan, LU Xinzheng. Nonlinear analysis method for seismic responses considering pounding between girders of curved bride with LRBs[J]. Journal of Civil，Architectural & Environmental Engineering，2012(5)：17-24.

[13] 黄小国,李建中,张哲. 连续梁桥纵桥向防落梁装置结构模式对比研究[J]. 同济大学学报(自然科学版),2009(9):1146-1152. HUANG Xiaoguo, LI Jianzhong, ZHANG Zhe. Comparative research on modes of longitudinal unseating prevention system for continuous bridge[J]. Journal of TongJi university (natural science),2009(9):1146-1152.

[14] 焦驰宇,龙佩恒,李士锣,等. 地震作用下中小跨度梁桥横向碰撞参数影响分析[J]. 振动与冲击,2014,33(8):48-53. JIAO Chiyu， LONG Peiheng， LI Shiluo,et al. Parametric analysis of transverse collision in middle and small span bridges under earthquake excitation[J]. Journal of Vibration and Shock, 2014,33(8):48-53.

[15] 邹立华,郭润,黄凯,等.带预应力橡胶支座相邻隔震结构碰撞分析[J].振动与冲击,2014,33(9):131-136. ZOU Lihua, GUO Run, HUANG Kai, et al. Pounding of adjacent isolated-structures with prestressed rubber bearings[J]. Journal of Vibration and Shock,2014,33(9):131-136.

Influences of displacement limitation of anchor bolt and adjacent beam collision on aseismic performance of a curved bridge

JIAO Chiyu1,3, XIAO Xiang1, LONG Peiheng2, XU Yan3, HOU Suwei2, ZHANG Yu1

(1. Beijing Municipal Urban Transportation Infrastructure Engineering Technology Research Center, BUCEA Beijing 100044, China；2. Beijing Collaborative Innovation Center for Technology of Energy Saving and Emission Reduction, BUCEA Beijing 100044, China；3. State Key Laboratory of Disaster Prevention in Civil Engineering, Tongji University, Shanghai 200092, China)

Non-uniform collisions happen among girders of curved bridges under seismic action to cause girder falling of front beams or local failure of back beams. Aseismic anchor bolts set in the longitudinal direction can effectively prevent girder falling and also have a mitigative effect on adjacent beam collision. Taking a 4-span curved bridge as an example, here its spatial finite element model was built. The time-delay system, hook element, contact element were used to simulate bearing damage, anchor bolt constraints, adjacent beam longitudinal collision. With the nonlinear time history analysis method, the comparatively studying relative displacements between pier and beam, internal force of pier bottom and adjacent beam collision force under three conditions including no anchor bolt and regardless of collision, no anchor bolt and considering collision and considering anchor bolt and collision was performed. The results showed that the adjacent beam non-uniform collision is the key factor that must be considered in a curved bridge; seeting aseismic anchor bolt can alleviate collision effects of a curved bridge and has a significant action for reducing seismic damage.

curved bridge; adjacent beam collision; aseismic anchor bolt; aseismic performance

国家青年自然科学基金(51308027);北京市自然科学基金(8162012);土木工程防灾国家重点实验室开放基金资助(SLDRCE-14-02);北京市教委科技计划面上项目(KM201310016007);北京市属高等学校创新团队建设与教师职业发展计划项目(IDHT20130512)

2015-08-03 修改稿收到日期：2016-01-27

焦驰宇 男，博士，副教授，1980年生

龙佩恒 男，博士，教授，1964年生

U441+.3