底部带有屈曲约束支撑的摇摆墙框架结构抗震性能分析
2017-01-10冯玉龙孟少平
冯玉龙 , 吴 京 , 孟少平, 王 强 ,2, 付 康
(1.东南大学 土木工程学院,南京 210096; 2.香港华艺设计顾问(深圳)有限公司南京分公司,南京 210037)
底部带有屈曲约束支撑的摇摆墙框架结构抗震性能分析
冯玉龙1, 吴 京1, 孟少平1, 王 强1,2, 付 康1
(1.东南大学 土木工程学院,南京 210096; 2.香港华艺设计顾问(深圳)有限公司南京分公司,南京 210037)
为减小摇摆墙框架结构强震下位移响应及缓解屈曲约束支撑框架的损伤集中效应,基于损伤集中模式,提出了底部带有屈曲约束支撑的摇摆墙框架结构体系。以9层钢框架为基准模型,通过推覆分析和动力时程分析对比研究了该结构体系的抗震性能。分析结果表明:BRB屈服前,该结构体系类似框剪结构,BRB提供抗侧刚度并通过墙体进行传递;BRB屈服后,结构发生摇摆,墙体控制变形模式,BRB通过滞回耗能,可以充分发挥结构各部分的抗震能力。
屈曲约束支撑;摇摆墙框架结构;推覆分析;动力时程分析;抗震性能
在结构中弱化基础对墙体的嵌固,使其在强震下墙脚能够上抬产生摇摆效应形成摇摆结构体系,有助于减小地震破坏[1]。屈曲约束支撑(Buckling-Restrained Brace, BRB)在受拉和受压时都可屈服而不屈曲,具有稳定的滞回耗能能力和较大的延性,克服了传统支撑受压失稳的缺点[2]。目前,摇摆结构体系和BRB在结构工程中均得到广泛应用[3-6]。
曹海韵等[7]指出摇摆墙可显著提高框架结构整体承载力及延性,可使层间变形趋于均匀,防止层倒塌模式。曲哲等[8]的研究指出了仅仅在框架结构中增加摇摆墙后结构的自振周期变化很小,摇摆墙-框架组合结构存在抗侧刚度偏弱、地震位移响应偏大的缺点,虽然层间变形分布均匀,但是仍然较难达到设计目标。文献[9-10]指出传统屈曲约束支撑屈服后刚度较低,屈曲约束支撑框架存在层变形集中和震后残余变形较大等问题。为了提高摇摆墙-框架结构和屈曲约束支撑框架结构的抗震性能,只有通过加大框架梁柱的截面才能够达到目的,这显然是不经济的。
将摇摆墙与BRB结合起来,使摇摆墙控制变形模式、BRB提供抗侧刚度和滞回阻尼,可以较好地解决上述问题。将BRB放在结构的底部可以有效地控制结构的损伤部位和损伤程度,损伤集中模式使结构震后易修复。基于此,本文提出了底部带有BRB的摇摆墙框架结构体系,并以9层钢框架为基准模型,利用OpenSees软件对该结构体系、剪力墙框架和摇摆墙框架的抗震性能进行了对比分析。
1 结构体系概念
1.1 结构布置
虽然BRB具有良好的抗震性能,但是将其应用到多层和高层结构中时,在地震作用下各楼层的BRB很难同时屈服耗能。BRB屈服后刚度较低,一旦有的楼层率先屈服,则薄弱层的形成无法避免。另一方面,由于摇摆墙框架结构中,摇摆墙的加入基本不为原框架提供抗侧刚度,而起到的是传递抗侧刚度的作用,虽然层间变形分布均匀,但是地震位移响应较大。因此,利用摇摆墙在摇摆过程中变形模式的确定性,可以在预期损伤部位(如结构底部)设置耗能构件来耗能。
图1为本文提出的底部带有BRB的摇摆墙框架结构体系的布置图和变形示意图。结构体系由摇摆墙、框架和BRB三个部分组成,其中摇摆墙墙体可以相对于墙底的一个固定的铰发生转动,也称为铰支墙。当BRB布置在摇摆墙底部时,两者组合称为底部带有BRB的摇摆墙(Hinged Wall with BRBs in Base,HWBB),本文称其与框架的组合为底部带有BRB的摇摆墙框架(HWBB Frame,HWBBF),如图1(a)所示。当BRB布置在框架楼层间时,可以选择沿楼层均匀布置BRB或仅在底层布置BRB,前者基于损伤均匀模式,震后需要修复或者替换较多的BRB构件,而后者和HWBBF一样均基于损伤集中模式,震后只需替换底层BRB构件。由于摇摆墙具有传递抗侧刚度的能力,理论上BRB布置在任意楼层均可以提供等价的抗侧刚度。为了和HWBBF对比,本文也探讨了BRB布置在框架底层层间的形式(Hinged Wall Frame with BRBs in Base,HWFBB),如图1(b)所示。

图1 底部带有BRB的摇摆墙框架结构示意图
1.2 抗震机制
该结构体系是“耗”和“调”两种抗震机制的组合。其中,“耗”就是在结构中加入耗能装置,消耗吸收地震能量,从而避免主体结构的严重破坏。而对于摇摆墙,它利用自身强大的抗弯刚度迫使结构发生均匀的层间变形,控制结构的变形模式,具有一种传递抗侧刚度协调结构变形的能力,可简称为“调”。
该结构体系中框架、BRB和摇摆墙三部分分工明确:框架主要承担竖向力,BRB提供抗侧刚度并在遭遇大震时耗能,摇摆墙则传递抗侧刚度并控制变形模式。合理的功能分化可以充分利用不同部分的特性,提高结构的整体抗震性能。遭遇小震时,BRB和摇摆墙组合起来发挥类似普通剪力墙的作用,提高结构的抗侧刚度并控制变形模式;遭遇中震或大震时,作为预期损伤构件的BRB进入塑性阶段,并利用优良的滞回特性进行有效的耗能,摇摆墙发生摇摆并保证结构层间变形分布均匀;震后,可以使用千斤顶调整摇摆墙的姿态,利用摇摆墙的巨大刚度迫使整体结构变形恢复至初始状态,之后可更换BRB构件。
2 HWBB几何关系推导
图2为HWBB的构造细节。图2中,在HWBB墙底对称布置两根相同的BRB,其间距为B,L1为BRB总长度,L0为核心板约束屈服段长度,A1为核心板连接段截面积,A0为核心板约束屈服段截面积。当BRB拉伸或者压缩长度为u时,墙体对应产生的转角为θb,显然θb等于u除以B/2。

图2 HWBB的构造细节
单根BRB的屈服承载力Fy、轴向弹性刚度k、屈服位移uy分别为:
Fy=fyA0
(1)
(2)
(3)
式中:fy为BRB核心板钢材的屈服应力,E为BRB核心板钢材的弹性模量。
当墙底的BRB简化为附着于墙底转动铰上的具有转动刚度的非线性弹簧时,根据几何关系,可以分析得到非线性弹簧的屈服弯矩My、转动刚度kb和屈服转角θb分别为:
My=fyA0B
(4)
(5)
(6)
在HWFBB中,BRB布置在框架底层,其底层的屈服位移角θy,brb为:
(7)
由于BRB核心板的弹性模量E和BRB与框架梁的夹角θ范围有限,其屈服位移角主要由BRB的屈服强度fy决定,相比而言,底部BRB间距B的可优化范围较大。因此,HWBBF的墙底屈服转角具有更广的选择范围。
3 结构模型
3.1 对比模型
图3中框架部分为简化的二维SAC-9钢框架[11],地下1层,地上9层,地下室层高为3.65 m,底层层高为5.49 m,其余各层层高均为3.96 m,柱距为9.15 m。柱和地面基础固接,地下室柱和底板铰接,柱的两层留有一个接头,接头和下层楼板的距离为1.83 m。楼层质量和梁、柱截面尺寸详见图3。在OPENSEES中建立了结构的数值模型,将模态分析得到的结构前5阶自振频率与ASCE结构控制委员会采用MATLAB仿真计算的结果进行对比(见表1)。从表1可知,两者基本相同,说明数值模型是合理的。
表1 钢框架周期
Tab.1 Period of steel frame

阶次12345ASCE/s2.25730.84750.48780.32360.2342OpenSees/s2.25750.84830.48830.32170.2337

图3 四种对比模型
在上述9层BENCHMARK模型(Frame, F)的基础上,通过增加摇摆墙、剪力墙、BRB分别建立摇摆墙框(Rocking Wall Frame, RWF)、剪力墙框架(Shear Wall Frame, SWF)、底层框架带有BRB的摇摆墙框架(HWFBB)和摇摆墙底部带有BRB的摇摆墙框架(HWBBF),四种结构如图3所示。结构框架部分的梁、柱屈服强度分别为248 MPa和345 MPa,弹性模量为2.06×105MPa;摇摆墙和剪力墙截面相同,以墙体和框架刚度比为设计原则,取墙体厚度和宽度分别为400 mm和3 680 mm,均采用C40混凝土,剪力墙屈服弯矩为3.50×104kNm;在HWFBB中,BRB的截面面积为7 900 mm2,屈服强度为300 N/mm2,弹性模量为2.06×105MPa;在HWBBF中,底部一对BRB被视为在铰的转动自由度上添加非线性弹簧,其初始刚度为1.8×107kNm,屈服弯矩为3.82×104kNm。
3.2 数值模型
梁柱构件使用基于柔度法的非线性梁柱单元,纤维材料采用双线性模型,其屈服后刚度比设为0.01。摇摆墙在大震下的设防目标是保持弹性,因此墙体采用弹性梁柱单元。剪力墙采用非线性梁柱单元,其中混凝土纤维采用CONCRETE01模型,钢筋纤维采用双线性模型;BRB使用桁架单元,采用双线性模型,其屈服后刚度比设为0.01。为了方便建模和对比图3中四种模型底层的墙体内力,HWBB采用底部带有一个非线性弹簧的弹性纤维梁单元模拟,弹簧采用零长度单元模拟。所有的非线性分析均考虑重力二阶效应。对比模型的前三阶周期列于表2,可以看出,摇摆墙的加入基本不改变结构的第一周期,但是在底层附加抗侧刚度或者在墙底附加转动刚度后,结构的整体刚度提高。其次,由于墙体的抗弯刚度很大,导致几种结构高阶周期均明显减小。
表2 对比模型周期
Tab.2 Period of contrast models

阶次123F/s2.25750.84830.4883RWF/s2.24210.65460.3198SWF/s1.85270.55250.2995HWFBB/s1.95650.59100.3047HWBBF/s1.95650.58730.3080
4 推覆分析
4.1 基底剪力-顶点位移曲线
采用倒三角荷载模式对结构进行非线性推覆分析。对比模型的基底剪力-顶点位移关系曲线如图4所示。由图可知,框架屈服前,RWF与F的力位移曲线基本重合,即两者的抗侧刚度基本相同,表明摇摆墙基本不为原结构提供抗侧刚度;框架屈服后,RWF的承载力继续增长,略大于F的承载力,F的承载力达到峰值后下降较快,而RWF下降较缓,表明摇摆墙迫使各层框架均能达到屈服,充分发挥了结构整体的延性和抗震能力。HWFBB、HWBBF和SWF的力位移曲线较为接近,其初始刚度和屈服承载力均要大于RWF和F,屈服后结构承载力没有出现下降趋势,具有和RWF类似的整体延性。值得注意的是,SWF结构中框架屈服后,由于剪力墙底部塑性铰的出现,其变形趋势和延性与摇摆墙框架相似,但是实际工程中,剪力墙底部塑性铰的延性转动能力比较有限。而由BRB简化的塑性铰的延性显然要优于剪力墙的底部塑性铰,HWBBF结构的整体延性也优于SWF结构。
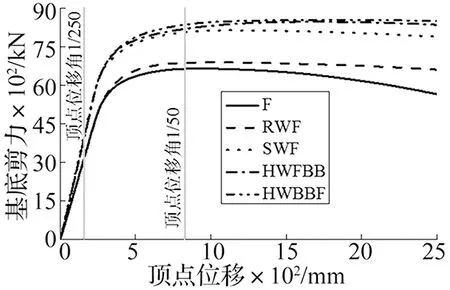
图4 基底剪力-顶点位移关系曲线
4.2 层间位移
以层间位移不均匀系数(Drift Concentration Factor,DCF)衡量结构的损伤集中效应,见式(8)。式中,θmax为最大层间位移角,uroof为顶点位移,H为结构总高度。
(8)
对比模型的DCF与顶点位移的关系曲线如图5所示。由图5可知,当顶点位移较小时,即结构处于弹性状态时,各种结构的变形均较为均匀。当结构进入非线性状态时,框架的DCF随着顶点位移的增加而增大,其他结构的DCF≈1。顶点位移较大时带有墙体的结构DCF较小,这主要是由于随着框架的逐步屈服,墙体的刚度相对于框架屈服后刚度较大,其控制结构变形模式的能力开始发挥。图6为结构顶点位移为2 000 mm时结构的层间位移角分布,可以看出HWFBB、HWBBF、RWF和SWF的层间位移分布较均匀,而F在第二楼层处出现了明显的薄弱层。

图5 DCF与顶点位移关系曲线

图6 层间位移角
4.3 层剪力-层间位移曲线

图7 层剪力与层间位移角关系曲线
对比结构的层剪力与层间位移角关系曲线如图7所示。图中从上至下依次为底层至顶层的层间力位移曲线。由图7(a)可知,由于P-Δ效应,F的下部楼层屈服后,层间剪力很快出现减小的趋势以维持结构在不断增大的二阶效应下的平衡。下部楼层在整个推覆过程中层间位移角始终增大,而上部楼层的层间位移角先增大后减小,经历了卸载过程。特别是顶层,整个加载和卸载过程中基本处于弹性状态。由于底部几层出现薄弱层,在结构达到承载力峰值时,上部几层的层间位移角非常小,远没有发挥其抗震能力。
带有墙体的结构中,各层的层间位移角发展速度基本相同,这主要是由于摇摆墙和剪力墙传递抗侧刚度的作用,各层框架均进入屈服阶段。
5 动力时程分析
5.1 地震波的选择
对结构进行动力时程分析,了解各种结构在地震动作用下的响应。时程分析采用文献[12]推荐的22条地震波,将所有地震波峰值加速度均调至4 m/s2。图8为22条地震波的加速度反应谱与设计谱的对比。

图8 实际地震波反应谱和设计谱的对比
5.2 结构位移响应
图9为22条地震波下的对比结构地震位移响应峰值,其平均值列于表3。从表3可知,由于在框架结构中加入摇摆墙并不能有效地改变结构的周期,摇摆墙框架的顶点位移和框架结构相近;而摇摆墙可以控制变形模式,摇摆墙框架的层间位移角和DCF均小于框架结构。本文提出的HWFBB和HWBBF的位移响应和框架剪力墙结构相似,其顶点位移和层间位移角均小于框架结构和摇摆框架结构。框架结构的DCF最大,表明变形向某些楼层集中,而各种墙体的加入可以有效地减小DCF。总体上,SWF、HWFBB和HWBBF结构的抗震性能优于F和RWF结构。
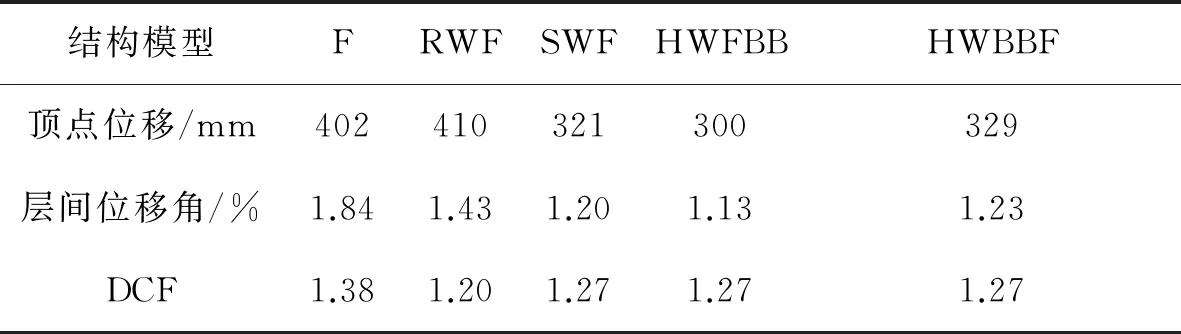
表3 结构平均位移响应

图9 结构位移响应
图10为第17条地震波下对比结构的层间位移角分布图。由图可知,框架结构的层间位移较大且分布不均匀,摇摆墙可以均匀框架的层间位移分布,但层间位移角的降低幅度有限;而本文提出的HWFBB和HWBBF结构的层间位移角大小及其分布和框架剪力墙结构相似,与框架结构相比,层间位移角较小且分布均匀。与SWF相比,HWFBB和HWBBF避免了普通剪力墙底部塑性铰的延性转动能力较低,破坏后难以修复等问题。
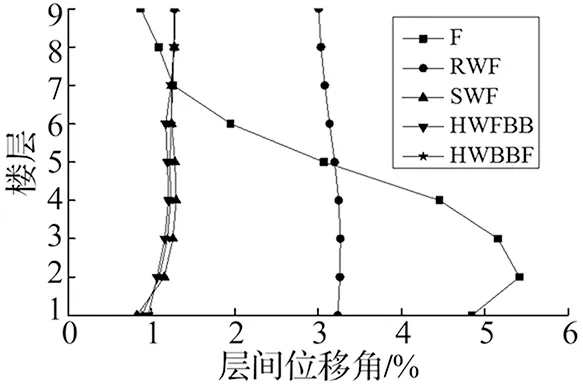
图10 第17条地震波下层间位移角
5.3 BRB滞回响应
图11为HWFBB中BRB和HWBB墙底非线性弹簧在22条地震波下的延性需求。BRB和非线性弹簧的平均延性需求分别为4.95和2.28。图12(a)和图12(b)分别为第12条地震波下HWFBB中一根BRB的滞回曲线和HWBB墙底非线性弹簧的滞回曲线。由图12可知,大多数地震波下两种结构中的BRB均能屈服,可以提供有效的滞回耗散地震能量。
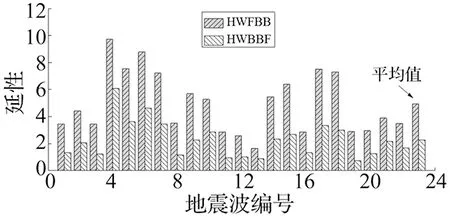
图11 BRB和非线性弹簧的延性需求

图12 第17条地震波下BRB和非线性弹簧的滞回响应
5.4 墙体内力分布
图13(a)和图13(b)分别为第17条地震波下对比结构的墙体弯矩和剪力的分布图。由图可见,HWFBB的墙体内力分布和摇摆墙相似,弯矩中部最大、剪力底部最大;HWBBF的墙体内力分布和剪力墙相似,弯矩和剪力均底部最大。
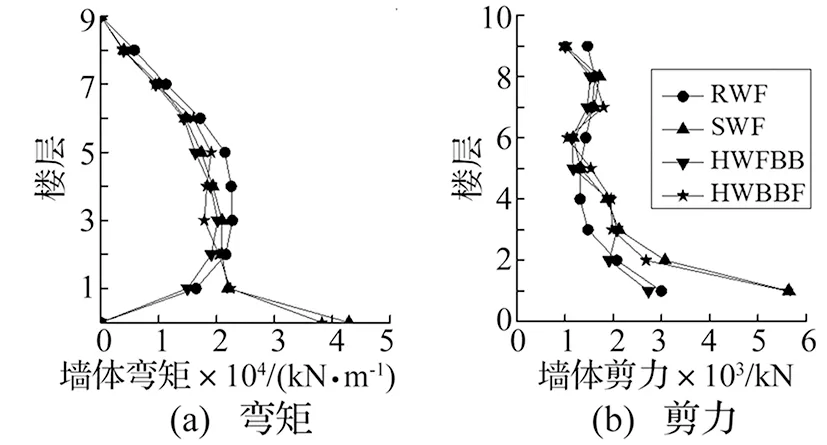
图13 第17条地震波下墙体内力
5.5 基底剪力
表4为对比结构在第17条地震波作用下的基底剪力峰值,包括BRB、墙体和框架承担剪力峰值以及基底总剪力峰值。由表可知,与框架F相比,加入墙体或者BRB会使结构的基底总剪力增加;RWF中框架承担剪力较大;对于SWF、HWFBB和HWBBF结构,虽然基底总剪力增大,但是墙体或BRB替框架分担了部分剪力,特别是HWFBB中,基底剪力主要由BRB承担,因此这些结构中框架承担的基底剪力小于原框架结构。

表4 第17条地震波下结构基底剪力峰值
6 结 论
(1)在底部带有BRB的摇摆墙框架结构体系中,BRB可以选择放在框架底层或者摇摆墙底部。框架主要承担竖向力,BRB提供抗侧刚度并在遭遇大震时耗能,摇摆墙则传递抗侧刚度、控制变形模式。
(2)推覆分析结果表明:底部带有屈曲约束支撑的摇摆墙框架结构体系,包括HWBBF和HWFBB,BRB屈服前类似框剪结构,BRB提供抗侧刚度并通过墙体进行传递,BRB屈服后结构发生摇摆,墙体控制变形模式。
(3)动力时程分析结果表明:BRB放在框架底层或者摇摆墙底部时,BRB均可以通过滞回耗能;底部带有BRB的摇摆墙结构的顶点位移、层间位移角响应和基底剪力与框架剪力墙结构相近,且DCF响应与摇摆墙框架结构相近,均比纯框架结构小。
[ 1 ] HOUSNER G W. The behavior of inverted pendulum structures during earthquakes [J]. Bulletin of the Seismological Society of America, 1963, 53(2): 403-417.
[ 2 ] UANG C M, NAKASHIMA M, TSAI K C. Research and application of buckling-restrained braced frames [J]. International Journal of Steel Structures, 2004, 4(4): 301-313.
[ 3 ] 周颖, 吕西林. 摇摆结构及自复位结构研究综述[J]. 建筑结构学报, 2011, 32(9): 1-10. ZHOU Ying, LÜ Xilin. State-of-the-art on rocking and self-centering structures [J]. Journal of Building Structures, 2011, 32(9): 1-10.
[ 4 ] 蒋欢军, 刘其舟. 可恢复功能剪力墙结构研究进展[J]. 振动与冲击, 2015, 34(7): 51-58. JIANG Huanjun, LIU Qizhou State-of-the-art of the research advances on resilient shear walls [J]. Journal of Vibration and Shock, 2015, 34(7): 51-58.
[ 5 ] 孙逊,崔永平,黄明,等. 人民日报社报刊综合业务楼结构设计[J]. 建筑结构,2012, 42(9): 52-55. SUN Xun, CUI Yongping, HUANG Ming, et al. Structural design of the people’s daily office building [J]. Building Structure, 2012, 42(9): 52-55.
[ 6 ] JONES P, ZAREIAN F. Seismic response of a 40-storey buckling-restrained braced frame designed for the los angeles region [J]. The Structural Design of Tall and Special Buildings, 2013, 22(3): 291-299.
[ 7 ] 曹海韵, 潘鹏, 叶列平. 基于推覆分析混凝土框架摇摆墙结构抗震性能研究[J]. 振动与冲击, 2011, 30(11): 240-244. CAO Haiyun, PAN Peng, YE Lieping. Pushover analysis of RC frame rocking wall structure [J]. Journal of Vibration and Shock, 2011, 30(11): 240-244.
[ 8 ] QU Z, WADA A, MOTOYUI S, et al. Pin-supported walls for enhancing the seismic performance of building structures [J]. Earthquake Engineering & Structural Dynamics, 2012, 41(14): 2075-2091.
[ 9 ] SABELLI R, MAHIN S, CHANG C. Seismic demands on steel braced frame buildings with buckling-restrained braces [J]. Engineering Structures, 2003, 25(5): 655-666.
[10] TREMBLAY R, LACERTE M, CHRISTOPOULOS C. Seismic response of multistory buildings with self-centering energy dissipative steel braces[J]. Journal of Structural Engineering, 2008, 134(1): 108-120.
[11] OHTORI Y, CHRISTENSON R E, SPENCER JR B F, et al. Benchmark control problems for seismically excited nonlinear buildings [J]. Journal of Engineering Mechanics, 2004, 130(4): 366-385.
[12] 曲哲. 摇摆墙-框架结构抗震损伤机制控制及设计方法研究[D]. 北京: 清华大学, 2010.
Aseismic performance analysis of rocking wall frame structures with buckling-restrained braces in base
FENG Yulong1, WU Jing1, MENG Shaoping1, WANG Qiang1,2, FU Kang1
(1. School of Civil Engineering, Southeast University, Nanjing 210096, China;2.Nanjing Branch, Hong Kong Hua Yi Design Consultants (Shenzhen) LTD., Nanjing 210037, China)
Based on a damage concentrated model, a rocking wall frame (RWF) structure system with buckling-restrained braces (BRBs) in base was put forward to reduce the displacement response of RWF under a strong earthquake and mitigate the damage concentration effect of a buckling-restrained braced frame (BRBF). Taking a 9-storey steel frame as the benchmark model, pushover analysis and dynamic time history analysis were conducted to comparatively study its aseismic performance. The results showed that before BRBs yield, this structure is similar to the shear wall frame (SWF), the additional lateral stiffness is provided by BRBs and transferred through the rocking wall; after BRBs yield, the structure tends to rock, the rocking wall controls the lateral deformation mode and BRBs consume seismic energy to lead to full use of the aseismic capacity of each part.
buckling-restrained brace; rocking wall frame structure; pushover analysis; dynamic time history analysis; aseismic performance
国家自然科学基金资助项目(51278105);江苏省普通高校研究生科研创新计划资助项目(KYLX_0153)
2015-07-22 修改稿收到日期:2015-11-12
冯玉龙 男,博士生,1990年生
吴京 男,博士,教授,1971年生
TU352.1
