磁场中轴向运动载流梁磁弹性主共振分析
2017-01-10胡宇达
王 杰, 胡宇达
(燕山大学 河北省重型装备与大型结构力学可靠性重点实验室,河北 秦皇岛 066004)
磁场中轴向运动载流梁磁弹性主共振分析
王 杰, 胡宇达
(燕山大学 河北省重型装备与大型结构力学可靠性重点实验室,河北 秦皇岛 066004)
研究磁场环境中轴向运动载流梁的磁弹性共振问题;考虑几何非线性,给出梁在力、运动、电磁作用下的动能、应变能以及电磁力的表达式。应用哈密顿变分原理,推得磁场中轴向运动载流梁的磁弹性振动方程。针对两端简支边界条件,假设三阶模态形函数,通过伽辽金积分推得梁的磁弹性振动微分方程;应用多尺度法,得到外激励力和外加电流作用下系统的主共振幅频响应方程;数值分析了磁感应强度、外加电流、轴向速度和外激励力对系统共振幅值的影响。结果表明,在振幅-磁感应强度响应图中,随着调谐参数的增大,共振曲线逐渐内缩最终上部封闭,外加电流使此变化过程中的临界分离点向右“偏移”。
磁弹性;导电梁;主共振;轴向运动;交变电流;多尺度法
轴向运动结构及器件在工程领域中应用较广,这些构件在电磁场环境中工作,将形成力、电、磁等多种效应间的相互耦合,影响系统运行的安全性和可靠性。为此引起研究者的关注并开展了深入的理论研究。CHEN等[1-2]研究了轴向运动粘弹性梁的非线性强迫振动问题,分析了轴向速度、边界条件等参数对结构振动频率及动力稳定性的影响。MA等[3]通过摄动法对悬臂梁的非线性振动进行准确求解,并将通过摄动法得到的结果与数值解进行比较;LESTARI等[4]通过不同边界条件获得屈曲梁非线性振动的准确解;胡海岩等[5]分析了内共振条件下直线运动梁的动力稳定性;张伟等[6]分析了黏弹性传动带1∶3内共振时的周期和混沌运动;陈树辉等[7]采用多元L-P法研究轴向运动梁横向非线性振动的内共振问题;PELLICANO[8]针对外激励载荷作用下轴向运动系统的复杂动态响应问题进行了研究;ARVIN等[9]研究了旋转复合材料梁的非线性自由振动问题。
另一方面,针对电磁场环境中复杂结构动力学的研究也引起人们广泛关注,从而促进了磁弹性力学理论的快速发展。PRATIHER等[10-11]分析了时变磁场中受周期载荷作用下悬臂梁的非线性共振问题;CHANG等[12]研究了弹性板在磁场中受到载荷作用下的非线性振动问题;WU[13]研究了横向磁场和热载荷作用下铁磁梁的大幅振动及动态稳定性问题;胡宇达等[14-15]建立了轴向运动导电板的非线性磁热弹性耦合振动方程,并针对其在周期外载荷作用下的非线性振动及混沌运动问题进行研究;刘信恩等[16]分析了几何非线性软铁磁导电梁式板在磁场中的动力响应问题。
本文在文献[17]的基础上研究磁场中轴向运动载流梁的磁弹性主共振问题,推得磁场中轴向运动载流梁的磁弹性振动方程,并针对梁的主共振问题进行分析。
1 磁场中轴向运动载电流弹性梁的振动方程
图1示出在横向恒定磁场B0(0,B0y,0)环境中做轴向运动的载电流弹性梁,其通入交变电流的密度矢量为J0(J0x,0,0),并受均布强迫激励Pz=f0sin(ωt)作用。其中,f0为外激励力幅值,ω为外激励力时变频率。梁长为l,高为h,宽为b,矩形横截面积为A=b×h,沿形心轴x方向运动速度为c。

图1 磁场中轴向运动载电流弹性梁
1.1 动能和势能
当轴向运动梁产生横向振动时,梁内各点沿z轴方向的速度分量为:
(1)
式中:w(x,t)为梁的横向位移,t为时间变量。
其总动能表达式为:
(2)
式中:ρ为材料质量密度。
依据弹性理论,考虑几何非线性,梁的势能包括轴向应变势能和梁的弯曲应变能,则梁的总势能表达式为:


1.2 电磁力和外力功
由电磁场理论可知,对于磁场环境中的载流梁,设J为梁内电流密度矢量,f为梁单位体积内电磁力矢量,则电磁力表达式为:
(4)
式中:J0x=j0sin(ω0t)为外加电流密度的分量,其中,j0为外加电流密度幅值,ω0为外加电流角频率。Jex=-σ0V0zB0y为因外加磁场作用而引起运动梁内感应电流密度分量(σ0为材料导电常数)。
对式(4)沿横截面积分,可得磁场环境中载流梁单位长度上电磁力为:
(5)
因此,外激励力Pz和电磁力Fz所做虚功之和为:
(6)
1.3 动力学方程
根据哈密顿变分原理,得出在横向磁场中轴向运动载电流弹性梁关于挠度的磁弹性振动方程为:
(7)
2 磁弹性主共振问题分析
2.1 振动微分方程
根据振动理论,采用模态叠加法,针对两端(x=0,l)简支约束情况,设满足边界条件的位移解为:
(8)
将式(8)代入式(7),由伽辽金法,推得P,t,ω无量纲化的横向振动微分方程组:
(9a)
(9b)
(9c)


2.2 应用多尺度法求解
采用多尺度法[18]研究系统的主共振问题,并在振动微分方程式(9)的等号右侧引入小参数ε。则一阶近似解可表示为:
(10)
式中:T1=τ、T2=ετ为引入的时间尺度。
将式(10)代入式(9)后展开,令ε的同次幂项系数相等,可得到:
关于ε0的近似方程:
(11a)
(11b)
(11c)
关于ε1的近似方程:
(12a)
(12b)
(12c)

设式(11)的通解形式为:
(13)

将式(13)代入式(12)得到:
(14a)
(14b)
(14c)
式中:cc为等式右侧各项的共轭。
2.2.1 外激励力和电流共同作用情况(Ω=Ω0)
研究外激励力频率分别接近系统前三阶固有频率的主共振问题。
(1)外激励力频率接近一阶固有频率
此时,外激励力频率为:Ω=Ω0=g1+εσ。其中σ为引入的频率调谐参数。由式(14)和欧拉公式可知,为避免久期项出现,必须令A满足:
(15)
对式(15)求解时,复函数An写成指数形式[18]:
(16)
其中,n=1,2,3。
然后,将式(16)代入式(15),分离实部与虚部,并令γ1=σT1-β1,可得:
(17)

(18)
(2)外激励力频率接近系统二阶固有频率
此时,外激励力频率为:Ω=Ω0=g2+εσ。同样由式(14)和欧拉公式可知,为避免久期项出现,应有:
(19)
同理可得:此时共振幅值a1,a2,a3都将衰减,其振动不会被激发。
(3)外激励力频率接近系统三阶固有频率
此时,外激励力频率为:Ω=Ω0=g3+εσ。同样由式(14)和欧拉公式可知,为避免久期项出现,应有:
(20)
同理可得:此时共振幅值a1,a2都将衰减,其振动不会被激发,而关于幅值a3的幅频响应方程为:
(21)
2.2.2 外激励力与电流单独作用情况
(1)载电流情况(无外激励力)
当系统的主共振仅由外加电流激发时,因无外激励力作用,只需在式(18)和式(21)中令外激励力幅值f0=0,即:k5=k7=0,可得到:
一阶主共振时,幅值a1的幅频响应方程为:
(22)
三阶主共振时,幅值a3的幅频响应方程为:
(23)
(2)外激励力作用情况(无外加电流)
当系统的主共振仅由外激励力激发时,因无外加电流的作用,只需在式(18)和式(21)中令外加电流密度j0=0,即:k6=k8=0,可得到:
一阶主共振时,幅值a1的幅频响应方程为:
(24)
三阶主共振时,幅值a3的幅频响应方程为:
(25)
3 算例分析
下面以铜制材料轴向运动载电流梁为例进行算例分析。主要参数取值为:梁长l=0.3 m,梁宽b=0.02 m,梁厚h=0.01 m,轴向拉力F0x=30 000 N,弹性模量E=108 GPa,质量密度ρ=8 920 kg/m3,电导率σ=5.714 3×107(Ω·m)-1。
3.1 外激励力作用情况(无外加电流)
当针对仅受外激励力作用梁的主共振问题计算分析时,应用的幅频响应方程式(24)和式(25),图2~图7分别给出了一阶和三阶共振振幅幅值与调谐参数、外激励力幅值、磁感应强度的关系曲线图。图8~图9给出了对应轴向运动系统的相平面轨迹曲线图。
图2和图3为不同轴向速度、磁感应强度、外激励力幅值时梁的一阶和三阶幅频曲线图。由图2(a)、图3(a)知,不同轴向速度所对应的幅频曲线在εσ=0附近存在交点,随着轴向速度的增大,共振幅值既有随之增大的区域,也有随之减小的区域。图2(b)、图3(b)和图2(c)、图3(c)表明,随磁感应强度的增大和激励力的减小,共振曲线主架呈现明显内缩且共振幅值减小趋势。

图2 一阶主共振幅频曲线图

图3 三阶主共振幅频曲线图
图4和图5为不同轴向速度、磁感应强度、调谐参数时梁的一阶和三阶振幅-外激励力幅值关系曲线图。图中曲线表明,受外激励力作用系统首先会出现多值现象,激励力增大到一定值后,解退化为较大的单值。同时,由图4(a)和图5(a)可知,随轴向速度的增大,在激励力幅值较小的单值区域内,共振振幅呈增大变化趋势;而在激励力幅大的单值区域内,共振振幅呈减小变化趋势。由图4(b)和图5(b)可知,在单值区域内,磁感应强度越大,共振振幅越小。

图4 一阶主共振振幅-外激励力曲线图

图5 三阶主共振振幅-外激励力曲线图

图6 一阶主共振振幅-磁感应强度曲线图

图7 三阶主共振振幅-磁感应强度响应图
图6和图7为不同轴向速度时梁的一阶和三阶振幅-磁感应强度曲线图。图中曲线均呈现关于B=0纵轴的左右对称形式。当磁感应强度增大到一定值时,振幅明显减小,多值性也会消失。同时,由图6(a)和图7(a)可知,曲线具有随轴向速度增大,曲线呈现对称内缩且幅值缓慢增大的变化规律。图6(b)和图7(b)中曲线表明,随着调谐参数值εσ的不断增大,共振曲线逐渐内缩并最终分离出上部的封闭曲线,其中,一阶主共振临界分离点为O1(εσ=0.618 9);三阶主共振临界分离点为O3(εσ=0.200 92)。
图8和图9为系统改变初始条件得到梁的动相平面轨迹,箭头表示轨迹的运动方向。图中表明系统发生一阶和三阶主共振时取不同的调谐参数值,稳定解的个数是不同的。图8(a)中只有一个稳定焦点S1,其共振幅值为as=0.021 5,记为S1(as=0.021 5);图8(b)中有两个稳定焦点S1(as=0.031 3)和S3(as=0.008),一个鞍点S2(as=0.017 6)。图9(a)中只有一个稳定焦点S1(as=0.002);图9(b)中有两个稳定焦点S1(as=0.005 2)和S3(as=0.001 1),一个鞍点S2(as=0.004 3)。可以看出图中稳定解的值与图2(a)和图3(a)中的值一致,其余的幅频特性曲线也有类似性质。

图8 一阶主共振梁的动相平面轨迹

图9 三阶主共振梁的动相平面轨迹
3.2 载电流情况(无外激励力)
当针对仅受外加电流作用梁的主共振问题计算分析时,应用幅频响应方程式(22),图10~图12分别给出了一阶共振幅值与调谐参数、外激励力幅值、磁感应强度的关系曲线图。
图10为不同轴向速度、磁感应强度、电流密度幅值、梁高的幅频曲线图。由图10(a)、图10(b)和图10(c)可知,随轴向速度和电流密度的减小、梁高度的增大,共振曲线主架呈现内缩趋势。图10(b)表明了磁感应强度对共振区域幅值有明显的影响:随磁感应强度的增强,共振曲线越平坦。

图10 一阶主共振梁的幅频曲线图
图11为不同轴向速度和磁感应强度的振幅-电流密度幅值曲线图。由图11可知,随轴向速度和磁感应强度的增大,共振振幅呈增大变化趋势。

图11 振幅-电流密度曲线图

图12 主共振振幅-磁感应强度曲线图
图12为不同轴向速度、调谐参数的振幅-磁感应强度曲线图。由图可见,曲线具有随轴向速度减小和调谐参数值εσ的不断增大,曲线呈现内缩且共振幅值减小的变化规律。
3.3 外激励力和外加电流共同作用情况
当针对受外激励力作用的载电流梁的主共振问题计算分析时,应用幅频响应方程式(18)和式(21),图13~图14分别给出了一阶和三阶共振幅值与磁感应强度的关系曲线图。与仅受外激励力作用梁的一阶和三阶共振幅值与磁感应强度的关系曲线图8和图9相比较,因受外加电流的影响,曲线均呈现相对B=0纵线的非对称分布形式。同时随调谐参数εσ的不断增大,共振曲线逐渐内缩最终上部封闭,同时发现此过程中的临界分离点O1和O3出现向右“偏移”的现象。

图13 一阶主共振振幅-磁感应强度曲线图
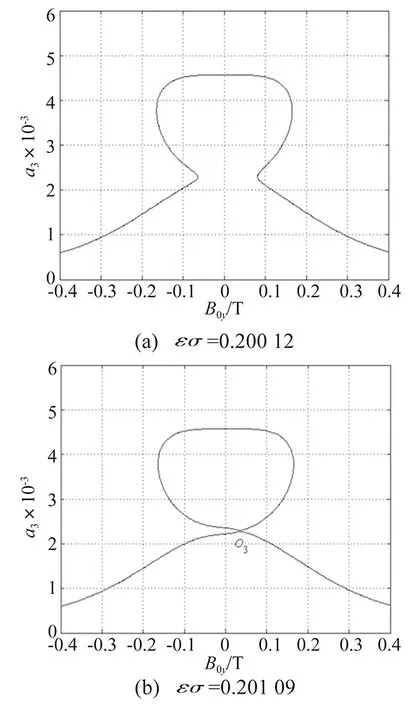
图14 三阶主共振振幅-磁感应强度曲线图
4 结 论
本文针对磁场中轴向运动载流弹性梁的共振问题,推导出其磁弹性振动方程,并得到了梁的幅频响应方程。通过数值算例,对两端简支梁的主共振问题进行了分析,结果表明:
(1)梁的轴向运动速度、高度、磁感应强度和外激励力对共振曲线均有显著影响,随外激励力幅值和轴向速度的增大,以及磁感应强度和梁高度的减小,梁的共振振幅呈增大趋势。
(2)相对于外激励力,材料允许范围内外加电流对梁的共振振幅的影响不明显。
(3)在振幅-磁感应强度响应图中,随着调谐参数值εσ的不断增大,共振曲线逐渐内缩最终上部封闭,而外加电流使此变化过程中的临界分离点向右“偏移”。
[ 1 ] CHEN L Q, TANG Y Q, LIMC C W. Dynamic stability in parametric resonance of axially accelerating viscoelastic Timonshenko beams[J]. Journal of Sound and Vibration, 2010, 329(5): 547-565.
[ 2 ] DING H, CHEN L Q. Galerkin methods for natural frequencies of high speed axially moving beams[J]. Journal of Sound and Vibration, 2010, 329(17): 3484-3494.
[ 3 ] MA X M, CHANG L Z, PAN Y T. Accurate solutions to nonlinear vibration of cantilever beam via homotopy perturbation method[J]. Procedia Engineering, 2011, 15(2): 4768-4773.
[ 4 ] LESTARI W, HANAGUD S. Nonlinear vibration of buckled beams some exact solutions International[J]. Journal of Solids and Structures, 2001, 38(1): 4741-4757.
[ 5 ] 冯志华, 胡海岩. 内共振条件下直线运动梁的动力稳定性[J]. 力学学报, 2002, 34(3): 389-400. FENG Zhihua HU Haiyan. Dynamic stability of a slender beam with internal resonance under a large linear motion[J]. Chinese Journal of Theoretical and Applied Mechanics, 2002, 34(3): 389-400.
[ 6 ] 张伟, 温洪波, 姚明辉. 黏弹性传动带1∶3内共振时的周期和混沌运动[J]. 力学学报, 2004, 36(4): 443-454. ZHANG Wei, WEN Hongbo, YANG Minghui. Periodic and chaotic oscillation of a parametrically excited viscoelastic moving belt with 1∶3 internal resonance[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(4): 443-454.
[ 7 ] 陈树辉, 黄建亮. 轴向运动梁非线性振动内共振研究[J]. 力学学报, 2005, 37(1): 57-63. CHEN Shuhui, HUANG Jiangliang. On internal resonance of nonlinear vibration of axially moving beams[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(1): 57-63.
[ 8 ] PELLICANO F.On the dynamic properties of axially moving systems[J]. Journal of Sound and Vibration, 2005, 281(3/4/5): 593-609.
[ 9 ] ARVIN H, BAKHTIARI-NEJAD F. Nonlinear free vibration analysis of rotating composite Timoshenko beams[J]. Composite and Structures, 2013, 96(12): 29-43.
[10] PRATIHER B. Nonlinear response of a magneto elastic translating beam with prismatic joint for higher resonance conditions[J]. International Journal of Nonlinear Mechanics, 2011, 46(5): 685-692.
[11] PRATIHER B, DWIVEDY S K. Nonlinear dynamics of a soft magneto elastic cartesian manipulator[J]. International Journal of Nonlinear Mechanics, 2009, 44(7): 757-768.
[12] CHANG T P, LIU M F. Nonlinear vibration analysis of an elastic plate subjected to heavy fluid loading in magnetic field International[J]. Journal of Solids and Structures, 2009, 46(7/8): 1705-1715.
[13] WU G Y. The analysis of dynamic instability on the large amplitude vibrations of a Beam with transverse magnetic fields and thermal loads[J]. Journal of Sound and Vibration,2007, 302(1/2): 167-177.
[14] 胡宇达, 张金志. 轴向运动载流导电板磁热弹性耦合动力学方程[J]. 力学学报, 2013, 45(5): 792-796. HU Yuda, ZHANG Jinzhi. Magneto-thermo-elastic couple dynamics equation of the axially moving current-carrying plant in magnetic field[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 792-796.
[15] HU Y D, HU P, ZHANG J Z. Strongly nonlinear subharmonic resonance and chaotic motion of axially moving thin plate in magnetic field[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(2): 0210101-0210112.
[16] 郑晓静, 刘信恩. 铁磁导电梁式板在横向均匀磁场中的动力特性分析[J]. 固体力学学报, 2000, 21(3): 243-250. ZHENG Xiaojing, LIU Xinen. Analysis on dynamic characteristics for ferromagnetic conducting plates in a transverse uniform magnetic field[J]. Acta Mechanica Solida Sinica, 2000, 21(3): 243-250.
[17] 胡宇达, 张立保. 轴向运动导电导磁梁的磁弹性振动方程[J]. 应用数学和力学, 2015, 36(1): 7-8. HU Yuda, ZHANG Libao. Magneto-elastic vibration equations for axially moving conductive and magnetic beams[J]. Applied Mathematics and Mechanics, 2015, 36(1): 7-8.
[18] 刘延柱, 陈立群. 非线性振动[M]. 北京: 高等教育出版社, 2001.
Magneto-elastic primary resonance of axially moving current-carrying beams in magnetic fieid
WANG Jie, HU Yuda
(Hebei Provincial Key Laboratory of Mechanical Reliability for Heavy Equipment and Large Structures,Yanshan University, Qinhuangdao 066004, China)
The magneto-elastic resonance of axially moving current-carrying beams in magnetic field was investigated. Considering the geometric nonlinearity and the interaction among force, motion, electric action and magnetic one, the expressions of kinetic energy, strain energy and electro-magnetic force were derived. Then with Hamilton princile, the vibration equation of an axially moving current-carrying beam in magnetic field was deduced. According to the simply supported boundary condition and assuming three orders modal shape functions, the magneto-elastic vibration differential equations of the beam were obtained through applying Galerkin integral method. Based on the method of multi-scale, the primary resonance amplitude-frequency response equations under external excitation and current of the system were gained. The influences of magnetic field strength, applied current, axial velocity, external motion on the amplitude of the system resonance were analyzed. The results showed that in the response plot of amplitude-intensity of magnetic field, with increase in tuning parameters, the resonance curve gradually retracts and its upper finally closes, the critical separation point in this varying process is shifted to the right due to the applied current.
magneto-elastic; conductive beam; primary resonance; axially moving; alternating current; multi-scale
国家自然科学基金项目(11472239);河北省自然科学基金项目(A2015203023);河北省高等学校科学技术研究重点项目(ZD20131055)
2015-10-12 修改稿收到日期:2015-11-10
王杰 男,研究生,1990年生
胡宇达 男,博士,教授,1968年生
O322;O442
